DOCSLIB.ORG

1101 Calculus I Lecture 2.6: Horizontal Asymptotes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1101 Calculus I Lecture 2.6: Horizontal Asymptotes Calculus Lecture 2.6: Horizontal Asymptotes Page 1 of 4 1101 Calculus I Lecture 2.6: Horizontal Asymptotes Note: We will not be using the precise definition of limits in this course. Vertical asymptotes are when we let x approach a number and the function f becomes arbitrarily large (positive or negative). For example, lim ln x = −∞ means y = ln x has a vertical asymptote at x = 0. x!0+ Horizontal asymptotes are when we let x become arbitrarily large (positive or negative) and the function f approaches a number. This is the more formal way to treat end behaviour, and allows us to examine more complicated functions than we have in the past (before we focussed mostly on rational functions, and said things like \4x5 − 3x + 1 is dominated by 4x5 when x is large"). Definition Let f be a function defined on some interval (a; 1). Then lim f(x) = L means that the values of f(x) can x!1 be made arbitrarily close to L by taking x sufficiently large. Definition Let f be a function defined on some interval (−∞; a). Then lim f(x) = L means that the values of f(x) can x→−∞ be made arbitrarily close to L by taking x sufficiently large negative. Definition The line y = L is called a horizontal asymptote of the curve y = f(x) if either lim f(x) = L; or lim f(x) = L: x!1 x→−∞ For example, the sketch of f(x) = tan−1 x shows two horizontal asymptotes: π π From the sketch, we see lim arctan x = , and lim arctan x = − . x!1 2 x→−∞ 2 Therefore, the horizontal asymptotes of f(x) = arctan(x) are y = π=2, and y = −π=2. Calculus Lecture 2.6: Horizontal Asymptotes Page 2 of 4 Theorems 1 If r > 0 is a rational number, then lim = 0. x!1 xr 1 If r > 0 is a rational number such that xr is defined for all x, then lim = 0. x→−∞ xr Technique: To evaluate a limit at infinity of a rational function or some algebraic functions, where both numerator and denominator are becoming large, we divide the numerator and denominator by the highest power of x in the denominator so we can use the two results above. We don't have to worry about division by zero since we are looking at very large x. 1 Note that is yet another indeterminant form. 1 x2 + 1 Example Evaluate lim . x!1 2x2 − 3x − 2 x2 + 1 1 lim ! indeterminant form, divide by largest power of x in denominator x!1 2x2 − 3x − 2 1 2 1 x + 1 2 = lim · x x!1 2 1 2x − 3x − 2 x2 1 + 1 = lim x2 x!1 1 1 2 − 3 x − 2 x2 1 + 0 = 2 − 3(0) − 2(0) 1 = 2 p Example Evaluate lim ( 9x2 + x − 3x). x!1 p lim ( 9x2 + x − 3x) −! 1 − 1 indeterminant form; need to do some algebra x!1 p p ( 9x2 + x + 3x) = lim ( 9x2 + x − 3x) · p x!1 ( 9x2 + x + 3x) (¨9x¨2 + x −¨9x¨2) = lim p x!1 ( 9x2 + x + 3x) x 1 = lim p ! divide by largest power of x in denominator x!1 ( 9x2 + x + 3x) 1 x 1=x = lim p · x!1 ( 9x2 + x + 3x) 1=x 1 p = lim p since x = x2 when x > 0 x!1 9x2 + x( p1 ) + 3 x2 1 = lim x!1 q 1 9 + x + 3 1 = p 9 + 0 + 3 1 = 6 Calculus Lecture 2.6: Horizontal Asymptotes Page 3 of 4 p 2x2 + 1 Example Find the horizontal asymptotes of the function: f(x) = . 3x − 5 p 2x2 + 1 1 lim = −! direct substitution does not work; indeterminant form x!1 3x − 5 1 p 2x2 + 1 1=x = lim · x!1 3x − 5 1=x p p 2x2 + 1 1= x2 p = lim · since x = x2 for x > 0 x!1 3x − 5 1=x p2 + 1=x2 = lim x!1 3 − 5=x p 2 + 0 = 3 − 0 p 2 = 3 p So y = 2=3 is a horizontal asymptote. p 2x2 + 1 1 lim = −! direct substitution does not work; indeterminant form x→−∞ 3x − 5 −∞ p 2x2 + 1 1=x = lim · x→−∞ 3x − 5 1=x p 2x2 + 1 1=(−px2) p = lim · since x = − x2 for x < 0 x→−∞ 3x − 5 1=x p2 + 1=x2 = − lim x→−∞ 3 − 5=x p 2 + 0 = − 3 − 0 p 2 = − 3 p So y = − 2=3 is a horizontal asymptote. Recall: lim ex = 1 and lim ex = 0. x!1 x→−∞ 1 − ex Example Evaluate lim . x!1 1 + 2ex 1 − ex −∞ lim ! indeterminant form; divide everything by ex, which is same as multiplying by e−x x!1 1 + 2ex 1 1 − ex e−x = lim · x!1 1 + 2ex e−x e−x − 1 = lim x!1 e−x + 2 0 − 1 −1 = = 0 + 2 2 1 − ex 1 − 0 Note that lim = = 1. x→−∞ 1 + 2ex 1 + 2(0) Calculus Lecture 2.6: Horizontal Asymptotes Page 4 of 4 p 9x6 − x Example Evaluate lim . x!1 x3 + 1 p 9x6 − x 1 lim ! indeterminant form x!1 x3 + 1 1 p 6 1 9x − x x3 = lim 3 · 1 x!1 x + 1 3 p x 9x6 − x p1 p = lim x6 since for x > 0, x3 = x6 x!1 1 1 + x3 q 1 9 − x5 = lim 1 x!1 1 + 3 p x 9 − 0 = 1 + 0 = 3 p 9x6 − x Example Evaluate lim . x→−∞ x3 + 1 Note that in this problem, we need lim (9x6 − x) = lim x(9x5 − 1) = (−∞)(−∞) = 1. x→−∞ x→−∞ p 9x6 − x 1 lim ! indeterminant form x→−∞ x3 + 1 −∞ p 6 1 9x − x x3 = lim 3 · 1 x→−∞ x + 1 3 p x 9x6 − x p1 p = − lim x6 since for x < 0, x3 = − x6 x→−∞ 1 1 + x3 q 1 9 − x5 = − lim 1 x→−∞ 1 + 3 p x 9 − 0 = − 1 + 0 = −3 −4x7 + 5 Example Evaluate lim . x!1 (x2 − 2)(2x2 − 1) −4x7 + 5 −∞ lim ! indeterminant form x!1 (x2 − 2)(2x2 − 1) 1 7 1 −4x + 5 4 = lim · x x!1 4 2 1 2x − 5x + 2 x4 −4x3 + 5 1 = lim x4 x!1 1 1 2 − 5 x2 + 2 x4 −4(1) + 5(0) = 2 − 5(0) + 2(0) = −∞ The limit does not exist..
Load more

Recommended publications
  • Section 3.7 Notes
    Section 3.7 Notes Rational Functions 1 Introduction Definition • A rational function is fraction of two polynomials. 2x2 − 1 • For example, f(x) = is a rational function. 3x2 + 2x − 5 Properties of Rational Graphs • The graph of every rational function is smooth (no sharp corners) • However, many rational functions are discontinuous . In other words, the graph might have several separate \sections" to the graph, similar to the way piecewise functions look. 1 For example, remember the graph of f(x) = x : Notice how the graph is drawn in two separate pieces. Asymptotes • An asymptote to a function is a line which the function gets closer and closer to without touching. • Rational functions have two categories of asymptote: 1. vertical asymptotes 2. asymptotes which determine the end behavior - these could be either horizontal asymp- totes or slant asymptotes Vertical Asymptote Horizontal Slant Asymptote Asymptote 1 2 Vertical Asymptotes Description • A vertical asymptote of a rational function is a vertical line which the graph never crosses, but does get closer and closer to. • Rational functions can have any number of vertical asymptotes • The number of vertical asymptotes determines the number of \pieces" the graph has. Since the graph will never cross any vertical asymptotes, there will be separate pieces between and on the sides of all the vertical asymptotes. Finding Vertical Asymptotes 1. Factor the denominator. 2. Set each factor equal to zero and solve. The locations of the vertical asymptotes are nothing more than the x-values where the function is undefined. Behavior Near Vertical Asymptotes The multiplicity of the vertical asymptote determines the behavior of the graph near the asymptote: Multiplicity Behavior even The two sides of the asymptote match - they both go up or both go down.
    [Show full text]
  • Vertical Tangents and Cusps
    Section 4.7 Lecture 15 Section 4.7 Vertical and Horizontal Asymptotes; Vertical Tangents and Cusps Jiwen He Department of Mathematics, University of Houston [email protected] math.uh.edu/∼jiwenhe/Math1431 Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 1 / 34 Section 4.7 Test 2 Test 2: November 1-4 in CASA Loggin to CourseWare to reserve your time to take the exam. Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 2 / 34 Section 4.7 Review for Test 2 Review for Test 2 by the College Success Program. Friday, October 24 2:30–3:30pm in the basement of the library by the C-site. Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 3 / 34 Section 4.7 Grade Information 300 points determined by exams 1, 2 and 3 100 points determined by lab work, written quizzes, homework, daily grades and online quizzes. 200 points determined by the final exam 600 points total Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 4 / 34 Section 4.7 More Grade Information 90% and above - A at least 80% and below 90%- B at least 70% and below 80% - C at least 60% and below 70% - D below 60% - F Jiwen He, University of Houston Math 1431 – Section 24076, Lecture 15 October 21, 2008 5 / 34 Section 4.7 Online Quizzes Online Quizzes are available on CourseWare. If you fail to reach 70% during three weeks of the semester, I have the option to drop you from the course!!!.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Apollonius of Pergaconics. Books One - Seven
    APOLLONIUS OF PERGACONICS. BOOKS ONE - SEVEN INTRODUCTION A. Apollonius at Perga Apollonius was born at Perga (Περγα) on the Southern coast of Asia Mi- nor, near the modern Turkish city of Bursa. Little is known about his life before he arrived in Alexandria, where he studied. Certain information about Apollonius’ life in Asia Minor can be obtained from his preface to Book 2 of Conics. The name “Apollonius”(Apollonius) means “devoted to Apollo”, similarly to “Artemius” or “Demetrius” meaning “devoted to Artemis or Demeter”. In the mentioned preface Apollonius writes to Eudemus of Pergamum that he sends him one of the books of Conics via his son also named Apollonius. The coincidence shows that this name was traditional in the family, and in all prob- ability Apollonius’ ancestors were priests of Apollo. Asia Minor during many centuries was for Indo-European tribes a bridge to Europe from their pre-fatherland south of the Caspian Sea. The Indo-European nation living in Asia Minor in 2nd and the beginning of the 1st millennia B.C. was usually called Hittites. Hittites are mentioned in the Bible and in Egyptian papyri. A military leader serving under the Biblical king David was the Hittite Uriah. His wife Bath- sheba, after his death, became the wife of king David and the mother of king Solomon. Hittites had a cuneiform writing analogous to the Babylonian one and hi- eroglyphs analogous to Egyptian ones. The Czech historian Bedrich Hrozny (1879-1952) who has deciphered Hittite cuneiform writing had established that the Hittite language belonged to the Western group of Indo-European languages [Hro].
    [Show full text]
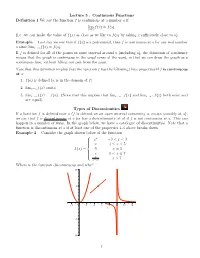
  • Lecture 5 : Continuous Functions Definition 1 We Say the Function F Is
    Lecture 5 : Continuous Functions Definition 1 We say the function f is continuous at a number a if lim f(x) = f(a): x!a (i.e. we can make the value of f(x) as close as we like to f(a) by taking x sufficiently close to a). Example Last day we saw that if f(x) is a polynomial, then f is continuous at a for any real number a since limx!a f(x) = f(a). If f is defined for all of the points in some interval around a (including a), the definition of continuity means that the graph is continuous in the usual sense of the word, in that we can draw the graph as a continuous line, without lifting our pen from the page. Note that this definition implies that the function f has the following three properties if f is continuous at a: 1. f(a) is defined (a is in the domain of f). 2. limx!a f(x) exists. 3. limx!a f(x) = f(a). (Note that this implies that limx!a− f(x) and limx!a+ f(x) both exist and are equal). Types of Discontinuities If a function f is defined near a (f is defined on an open interval containing a, except possibly at a), we say that f is discontinuous at a (or has a discontinuiuty at a) if f is not continuous at a. This can happen in a number of ways. In the graph below, we have a catalogue of discontinuities. Note that a function is discontinuous at a if at least one of the properties 1-3 above breaks down.
    [Show full text]
  • GRAPH of a RATIONAL FUNCTION Find Vertical Asymptotes and Draw
    GRAPH OF A RATIONAL FUNCTION Find vertical asymptotes and draw them. Look for common factors first. Vertical asymptotes occur where the denominator becomes zero as long as there are no common factors. Find the horizontal asymptote, if any, and draw it. A horizontal asymptote may be found using the exponents and coefficients of the lead terms in the numerator and denominator. Please see “Horizontal Asymptotes and Lead Coefficients” below. Pick two or three x-values to the left and right of each vertical asymptote . If there are no vertical asymptotes, then just pick 2 positive, 2 negative, and zero. Put these values into the function f(x) and plot the points. This will give you an idea of the shape of the curve. You will quickly see whether the graph goes above or below the horizontal asymptote . Find the y-intercept by letting x = 0 . Put “0” into the function, do the arithmetic and get the y-value. Plot the point ( 0, y ). This will show you where the curve crosses the y-axis. Find any x-intercepts by letting y = 0 . Replace f(x) by “0”, then solve for x. Plot these points as (x, 0 ). This will show you where the graph crosses the x-axis. By the way, when you set y =0 it is possible that you will get imaginary answers for x. Since we can not graph a + bi on the “real plane”, this means there are no x-intercepts. Finally, connect all of the points (x, y ) with a smooth curve rather than choppy, straight line segments.
    [Show full text]
  • MATH 12002 - CALCULUS I §1.6: Horizontal Asymptotes
    MATH 12002 - CALCULUS I x1.6: Horizontal Asymptotes Professor Donald L. White Department of Mathematical Sciences Kent State University D.L. White (Kent State University) 1 / 5 Horizontal Asymptotes Horizontal asymptotes are very closely related to limits at infinity. Definition Let y = f (x) be a function and let L be a number. The line y = L is a horizontal asymptote of f if lim f (x) = L or lim f (x) = L: x!+1 x→−∞ Notes: The definition means that the graph of f is very close to the horizontal line y = L for large (positive or negative) values of x. A function can have at most two different horizontal asymptotes. A graph can approach a horizontal asymptote in many different ways; see Figure 8 in x1.6 of the text for graphical illustrations. In particular, a graph can, and often does, cross a horizontal asymptote. Let's emphasize this point to avoid problems later: D.L. White (Kent State University) 2 / 5 Horizontal Asymptotes THERE'S NO REASON | HERE'S MY POINT, DUDE | THERE'S NO #^|%!*& REASON WHY THE GRAPH OF A FUNCTION CAN'T CROSS A HORIZONTAL ASYMPTOTE!! D.L. White (Kent State University) 3 / 5 Horizontal Asymptotes Our general result on limits at infinity of rational functions implies the following. Theorem P(x) Let f (x) = Q(x) be a rational function (P(x),Q(x) are polynomials). If deg P(x) = deg Q(x), then the horizontal asymptote of f (x) is p y = ; q where p, q are the leading coefficients of P(x),Q(x), respectively.
    [Show full text]
  • Section 9.2 Hyperbolas 597
    Section 9.2 Hyperbolas 597 Section 9.2 Hyperbolas In the last section, we learned that planets have approximately elliptical orbits around the sun. When an object like a comet is moving quickly, it is able to escape the gravitational pull of the sun and follows a path with the shape of a hyperbola. Hyperbolas are curves that can help us find the location of a ship, describe the shape of cooling towers, or calibrate seismological equipment. The hyperbola is another type of conic section created by intersecting a plane with a double cone, as shown below5. The word “hyperbola” derives from a Greek word meaning “excess.” The English word “hyperbole” means exaggeration. We can think of a hyperbola as an excessive or exaggerated ellipse, one turned inside out. We defined an ellipse as the set of all points where the sum of the distances from that point to two fixed points is a constant. A hyperbola is the set of all points where the absolute value of the difference of the distances from the point to two fixed points is a constant. 5 Pbroks13 (https://commons.wikimedia.org/wiki/File:Conic_sections_with_plane.svg), “Conic sections with plane”, cropped to show only a hyperbola by L Michaels, CC BY 3.0 598 Chapter 9 Hyperbola Definition A hyperbola is the set of all points Q (x, y) for which the absolute value of the difference of the distances to two fixed points F1(x1, y1) and F2 (x2, y2 ) called the foci (plural for focus) is a constant k: d(Q, F1 )− d(Q, F2 ) = k .
    [Show full text]
  • Rational Functions
    Rational Functions A rational function is a function of the form Px( ) rx()= Qx() where P and Q are polynomials. We assume that P(x) and Q(x) have no factors in common, and Q(x) is not the zero polynomial. Rational Functions and Asymptotes: Remember that a fraction is undefined if there is a zero in the denominator. Rational functions are not defined for those values of x for which the denominator is zero. When graphing a rational function, we must pay special attention to the behavior of the graph near those x-values. 1 The simplest rational function with a variable denominator is rx()= . x 1 Example 1: Sketch a graph of the rational function rx()= . x Solution: Step 1: First we note that the function r is not defined for x = 0. The number 0 cannot be used as a value of x, but for graphing it is helpful to find the values of f (x) for some values of x close to 0. We describe this behavior in words and in symbols as follows. The first table shows that as x approaches 0 from the left, the values of r (x) decrease without bound. In symbols, By: Crystal Hull Example 1 (Continued): Step 1: r (x) → – ∞ as x → 0– “y approaches negative infinity as x approaches 0 from the left” The second table shows that as x approaches 0 from the right, the values of r (x) increase without bound. In symbols, r (x) → ∞ as x → 0+ “y approaches infinity as x approaches 0 from the right” Step 2: Next, we want to look at the end behavior of the graph of 1 rx()= .
    [Show full text]
  • Barry Mcquarrie's Calculus I Glossary Asymptote: a Vertical Or Horizontal
    Barry McQuarrie’s Calculus I Glossary Asymptote: A vertical or horizontal line on a graph which a function approaches. Antiderivative: The antiderivative of a function f(x) is another function F (x). If we take the derivative of F (x) the result is f(x). The most general antiderivative is a family of curves. Antidifferentiation: The process of finding an antiderivative of a function f(x). Concavity: Concavity measures how a function bends, or in other words, the function’s curvature. Concave Down: A function f(x) is concave down at x = a if it is below its tangent line at x = a. This is true if f 00(a) < 0. Concave Up: A function f(x) is concave up at x = a if it is above its tangent line at x = a. This is true if f 00(a) > 0. Constant of Integration: The constant that is included when an indefinite integral is performed. Z b Definite Integral: Formally, a definite integral looks like f(x)dx. A definite integral when evaluated yields a number. a The definite integral can be interpreted as the net area under the function f(x) from x = a to x = b. d Derivative: Formally, a derivative looks like f(x), and represents the rate of change of f(x) with respect to the dx variable x. Anther notation for derivative is f 0(x). Differential: Informally, a differential dx can be thought of a small amount of x. Differentials appear in both derivatives and integrals. Differentiation: The process of finding the derivative of a function f(x).
    [Show full text]
  • Chapter 4 Rational Functions and Conics
    Chapter 4 Rational Functions and Conics Section 4.1 N(x) Rational function – A function that can be written in the form: f (x) = , where N(x) and D(x) are D(x) polynomials and D(x) is not the zero polynomial Vertical asymptote – The line x = a is a vertical asymptote of the graph of f if f(x) → ∞ or f(x) → –∞ as x → a , either from the right or from the left. Horizontal asymptote – The line y = b is a horizontal asymptote of the graph of f if f(x) → b as x → ∞ or x → –∞ Section 4.2 Slant (or oblique) asymptote – If the degree of the numerator of a rational function is exactly one more than the degree of the denominator, then the line determined by the quotient of the denominator into the numerator is a slant asymptote of the graph of the rational function Section 4.3 Partial fraction – A rational expression can be written as the sum of two or more simpler fractions. Each simpler fraction is called a partial fraction. Partial fraction decomposition – A rational expression written as the sum of two or more simpler rational expressions Basic equation – The equation that results when both sides of the form of a decomposition is multiplied by the least common denominator Section 4.4 Conic section or conic – The figure formed by the intersection of a plane and a double-napped cone Degenerate conic – Figure formed when a plane passes through the vertex of a double-napped cone Parabola – The set of all points (x, y) in a plane that are equidistant from a fixed line and a fixed point not on the line.
    [Show full text]
  • Glossary from Math Analysis
    A Glossary for Pre-calculus These terms were identified during the Cal-PASS deconstruction of the California State Standards for Math Analysis, Linear Algebra, and Trigonometry By the Cal-PASS Central San Diego Math Professional Learning Council Bruce Arnold, Brenda Kracht, Judy Ross, Terrie Teegarden and Maurice Tompkins 1 Preface: In the deconstruction of the California state standards for trigonometry, linear algebra and mathematical analysis for the Cal-PASS Content Standards Deconstruction projects, it became apparent that terms were used for which no definition was given. The San Diego Central Cal-PASS Math Professional Learning Council felt that many of these terms might be unfamiliar to a precalculus instructor. Hence, a list of key terms and their appropriate definitions were developed, resulting in this document. These descriptions are intended to be explanatory rather than to provide precise mathematical rigor. Some terms, such as logarithms, are not included even though they are essential for calculus preparation because they do not appear in the precalculus standards. Many high schools combine some of the standards from trigonometry, linear algebra, and mathematical analysis to form a pre-calculus course. Pre-calculus courses in community colleges and four year institutions also combine the content of these standards. This integrated approach reflects the fact that these topics do not exist in isolation, but rather work in unity with each other. It is also important to note that the order of the standards, or even groups of standards, may not reflect the order in which they might appear in standard textbooks or course outlines. Suggested topic sequence for a pre-calculus course: Mathematical Analysis 4 and 6 Note that there are many topics loosely associated with 4 that are not mentioned, such as the Rational Root Theorem, Descartes’ Rule of signs, etc.
    [Show full text]