Na¨Ive Regression Requires Weaker Assumptions Than Factor Models to Adjust for Multiple Cause Confounding ∗
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Not Your Mother's Library Transcript Episode 11: Mamma Mia! and More Musicals (Brief Intro Music) Rachel: Hello, and Welcome T
Not Your Mother’s Library Transcript Episode 11: Mamma Mia! and More Musicals (Brief intro music) Rachel: Hello, and welcome to Not Your Mother’s Library, a readers’ advisory podcast from the Oak Creek Public Library. I’m Rachel, and once again since Melody’s departure I am without a co-host. This is where you would stick a crying-face emoji. Luckily for everyone, though, today we have a brand new guest! This is most excellent, truly, because we are going to be talking about musicals, and I do not have any sort of expertise in that area. So, to balance the episode out with a more professional perspective, I would like to welcome to the podcast Oak Creek Library’s very own Technical Services Librarian! Would you like to introduce yourself? Joanne: Hello, everyone. I am a new guest! Hooray! (laughs) Rachel: Yeah! Joanne: So, I am the Technical Services Librarian here at the Oak Creek Library. My name is Joanne. I graduated from Carroll University with a degree in music, which was super helpful for libraries. Not so much. Rachel: (laughs) Joanne: And then went to UW-Milwaukee to get my masters in library science, and I’ve been working in public libraries ever since. I’ve always had a love of music since I've been in a child. My mom is actually a church organist, and so I think that’s where I get it from. Rachel: Wow, yeah. Joanne: I used to play piano—I did about 10 years and then quit. (laughs) So, I might be able to read some sheet music but probably not very well. -

Cultural Commentary: Affectional Preference on Film: Giggle and Lib Joseph J
Bridgewater Review Volume 1 | Issue 2 Article 9 Dec-1982 Cultural Commentary: Affectional Preference on Film: Giggle and Lib Joseph J. Liggera Bridgewater State College Recommended Citation Liggera, Joseph J. (1982). Cultural Commentary: Affectional Preference on Film: Giggle and Lib. Bridgewater Review, 1(2), 21-22. Available at: http://vc.bridgew.edu/br_rev/vol1/iss2/9 This item is available as part of Virtual Commons, the open-access institutional repository of Bridgewater State University, Bridgewater, Massachusetts. CULTURAL COMMENTARY Affectional Preference on Film: Giggle and Lib omantic attachments on screen the romantic man whose passionate desire With the great artist abandoning R these days require at least a hint of is for a person unquestionably of the romantic love--Bergman has lately something kinky to draw the pop audience opposite sex. So straight are his lusts that announced that his next two films will be his which in the days of yesteryear thrilled to no one seemed to notice the dilemma posed last--leaving the field to an oddity like Allen Bogart and Bacall, but which now winks in Manhattan of a man in his mid-forties or television's "Love Boat", the pop knowingly at Julie Andrews in drag. having physical congress with a fifteen year audience, which never warmed to Bergman Something equally aberrant, in fact moreso, old. This year, A -Midsummer Night's Sex or his like anyway, might find solace in Blake more blatant and proselytizing, quickens Comedy renders two points of sexual Edwards, an intriguing director whose last the mental loins of the liberal film-going metaphysics for those still lost in memories three films and his wife's, Julie Andrews, mind; anything less denies the backbone of a gender-differentiated past, the first changing image in them illustrate a syn upon which liberal sentiments are oddly enough insisted upon by the women: if thesis of audience demands with a structured. -

Pulp Fiction © Jami Bernard the a List: the National Society of Film Critics’ 100 Essential Films, 2002
Pulp Fiction © Jami Bernard The A List: The National Society of Film Critics’ 100 Essential Films, 2002 When Quentin Tarantino traveled for the first time to Amsterdam and Paris, flush with the critical success of “Reservoir Dogs” and still piecing together the quilt of “Pulp Fiction,” he was tickled by the absence of any Quarter Pounders with Cheese on the European culinary scene, a casualty of the metric system. It was just the kind of thing that comes up among friends who are stoned or killing Harvey Keitel (left) and Quentin Tarantino attempt to resolve “The Bonnie Situation.” time. Later, when every nook and cranny Courtesy Library of Congress of “Pulp Fiction” had become quoted and quantified, this minor burger observation entered pop (something a new generation certainly related to through culture with a flourish as part of what fans call the video games, which are similarly structured). Travolta “Tarantinoverse.” gets to stare down Willis (whom he dismisses as “Punchy”), something that could only happen in a movie With its interlocking story structure, looping time frame, directed by an ardent fan of “Welcome Back Kotter.” In and electric jolts, “Pulp Fiction” uses the grammar of film each grouping, the alpha male is soon determined, and to explore the amusement park of the Tarantinoverse, a the scene involves appeasing him. (In the segment called stylized merging of the mundane with the unthinkable, “The Bonnie Situation,” for example, even the big crime all set in a 1970s time warp. Tarantino is the first of a boss is so inexplicably afraid of upsetting Bonnie, a night slacker generation to be idolized and deconstructed as nurse, that he sends in his top guy, played by Harvey Kei- much for his attitude, quirks, and knowledge of pop- tel, to keep from getting on her bad side.) culture arcana as for his output, which as of this writing has been Jack-Rabbit slim. -

Smörgåsbord: Award Show Scandals
Smörgåsbord: Award Show Scandals Every year, media award shows like the Grammys, Emmys, and Oscars recognize the hard work put into a wide array of diverse movies, TV shows, songs, and albums. However, no event is perfect, and the mass anticipation for each show ensures that every rare on-stage slip-up is bound to make headlines is made that much more memorable when it occurs. With the 2018 Academy Awards having just recently passed, here’s a quick highlight reel of some of the most famous fumbles forever enshrined in award show history. La La Land Smörgåsbord: Award Show Scandals graphic by Amanda Shi An Oscar is one of the highest honors possible for a work of media. And of course, the more serious the award, the more shocking the slip-up, and there can be no greater (and thus unforgettable) mistake in an Oscars award show than presenting the wrong winner. In an absolutely unprecedented, history-making moment at the 89th Academy Awards, La La Land Smörgåsbord: Award Show Scandals was mistakenly called as winner of Best Picture. An envelope mix-up was to blame for starting the misunderstanding; the Best Actress in a Leading Role envelope had somehow been swapped with the Best Picture envelope. Warren Beatty had known something was wrong when he opened the card and read ‘Emma Stone, La La Land’, but he hadn’t known how to respond to such an unexpected scenario. In his confusion, he attempted to stall for time by pausing in between words, but both the audience and his co-presenter Faye Dunaway interpreted it as him deliberately building suspense. -
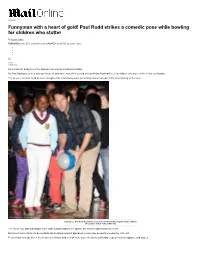
Paul Rudd Strikes a Comedic Pose While Bowling for Children Who Stutter
show ad Funnyman with a heart of gold! Paul Rudd strikes a comedic pose while bowling for children who stutter By Shyam Dodge PUBLISHED: 03:33 EST, 22 October 2013 | UPDATED: 03:34 EST, 22 October 2013 30 View comments He's known for being one of the funniest men working in Hollywood today. But Paul Rudd proved he's also got a heart of gold as he hosted his second annual All-Star Bowling Benefit for children who stutter in New York, on Monday. The 44-year-old actor could be seen throughout the fund raising event performing various comedic antics while bowling at the lanes. Gearing up: Paul Rudd hosted his second annual All-Star Bowling Benefit for children who stutter in New York, on Monday The I Love You, Man star taught some of the fundamentals of the sport to the children gathered for the event. But when it came his turn to demonstrate his bowling prowess it appeared he may have needed some practise in the art. Performing a comedic kick in the air after seeming to land the ball in the gutter the surrounding kids erupted into both applause and giggles. Getting a rise: The 44-year-old actor looked to have missed his mark during the event The set up: Rudd got his form down before letting loose But the antics also seemed to have been choreographed to entertain the youngsters, who the star was intent upon helping. Wearing brown suede loafers and tan chinos, Rudd went casual in a simple chequered button down shirt. -

State Visit of Queen Elizabeth II and Prince Phillip (Great Britain) (4)” of the Betty Ford White House Papers, 1973-1977 at the Gerald R
The original documents are located in Box 51, folder “7/7-10/76 - State Visit of Queen Elizabeth II and Prince Phillip (Great Britain) (4)” of the Betty Ford White House Papers, 1973-1977 at the Gerald R. Ford Presidential Library. Copyright Notice The copyright law of the United States (Title 17, United States Code) governs the making of photocopies or other reproductions of copyrighted material. Betty Ford donated to the United States of America her copyrights in all of her unpublished writings in National Archives collections. Works prepared by U.S. Government employees as part of their official duties are in the public domain. The copyrights to materials written by other individuals or organizations are presumed to remain with them. If you think any of the information displayed in the PDF is subject to a valid copyright claim, please contact the Gerald R. Ford Presidential Library. THE WHITE HOUSE WASHINGTON Proposed guest list for the dinner to be given by the President and Mrs. Ford in honor of Her Majesty Queen Elizabeth II and His Royal Highness The Prince Philip, Duke of Edinburgh, on Wednesday, July 7, 1976 at eight 0 1 clock, The White House. White tie. The President and Mrs. Ford Her Majesty Queen Elizabeth II and The Prince Philip Balance of official party - 16 Miss Susan Ford Mr. Jack Ford The Vice President and Mrs. Rockefeller The Secretary of State and Mrs. Kissinger The Secretary of the Treasury and Mrs. Simon The Secretary of Defense and Mrs. Rumsfeld The Chief Justice and Mrs. Burger General and Mrs. -

The Departed Talent: Matt Damon, Leonardo Dicaprio, Jack Nicholson
The Departed Talent: Matt Damon, Leonardo DiCaprio, Jack Nicholson, Mark Wahlberg, Alec Baldwin, Vera Farmiga, Martin Sheen, Ray Winstone. Date of review: Thursday the 12th of October, 2006. Director: Martin Scorsese Classification: MA (15+) Duration: 152 minutes We rate it: Five stars. For any serious cinemagoer or lover of film as an art form, the arrival of a new film by Martin Scorsese is a reason to get very excited indeed. Scorsese has long been regarded as one of the greatest of America’s filmmakers; since the mid-1980s he has been regarded as one of the greatest filmmakers in the world, period. With landmark works like Taxi Driver (1976), Raging Bull (1980), Goodfellas (1990) and Bringing Out the Dead (1999) to his credit, Scorsese is a director for whom any actor will go the distance, and the casts the director manages to assemble for his every project are extraordinarily impressive. As a visualist Scorsese is a force to be reckoned with, and his soundtracks regularly become known as classic creations; his regular collaborators, including editor Thelma Schoonmaker and cinematographer Michael Ballhaus are the best in their respective fields. Paraphrasing all of this, one could justifiably describe Martin Scorsese as one of the most important and interesting directors on the face of the planet. The Departed, Scorsese’s newest film, is on one level a remake of a very successful Hong Kong action thriller from 2002 called Infernal Affairs. That film, written by Felix Chong and directed by Andrew Lau, set the box office on fire in Hong Kong and became a cult hit around the world. -

Bcsfazine #528 | Felicity Walker
The Newsletter of the British Columbia Science Fiction Association #528 $3.00/Issue May 2017 In This Issue: This and Next Month in BCSFA..........................................0 About BCSFA.......................................................................0 Letters of Comment............................................................1 Calendar...............................................................................6 News-Like Matter..............................................................11 Turncoat (Taral Wayne)....................................................17 Art Credits..........................................................................18 BCSFAzine © May 2017, Volume 45, #5, Issue #528 is the monthly club newsletter published by the British Columbia Science Fiction Association, a social organiza- tion. ISSN 1490-6406. Please send comments, suggestions, and/or submissions to Felicity Walker (the editor), at felicity4711@ gmail .com or Apartment 601, Manhattan Tower, 6611 Coo- ney Road, Richmond, BC, Canada, V6Y 4C5 (new address). BCSFAzine is distributed monthly at White Dwarf Books, 3715 West 10th Aven- ue, Vancouver, BC, V6R 2G5; telephone 604-228-8223; e-mail whitedwarf@ deadwrite.com. Single copies C$3.00/US$2.00 each. Cheques should be made pay- able to “West Coast Science Fiction Association (WCSFA).” This and Next Month in BCSFA Friday 19 May: Submission deadline for June BCSFAzine (ideally). Sunday 14 May at 7 PM: May BCSFA meeting—at Ray Seredin’s, 707 Hamilton Street (recreation room), New Westminster. -

Once Upon a Time … in Santa Clarita: Tarantino Movie Opens Thursday
By: Caleb Lunetta, July 25, 2019 Once Upon a Time … In Santa Clarita: Tarantino movie opens Thursday Hollywood director Quentin Tarantino is known for his genre-defying blockbuster films that combine elements of art house, violence and comedy in his Academy Award-winning films. And the San Fernando Valley resident calls Santa Clarita “a special place,” according to local film property owners who have played host to the luminary for his latest film that debuts tonight, “Once Upon a Time … In Hollywood.” The latest installment in the Tarantino filmography follows the story of “a faded television actor and his stunt double (who) strive to achieve fame and success in the film industry during the final years of Hollywood’s Golden Age in 1969 Los Angeles,” according to IMDb.com. The film features Leonardo DiCaprio, Brad Pitt and Margot Robbie. Tarantino and movie fans were given a teaser trailer where the opening shot was that of Melody Ranch’s “Main Street” set. Veluzat said that the production team had been working with the studio for a couple months, from planning to setting up to filming, and for him, it was a special experience. Tarantino has filmed two of his last three movies at Melody Ranch in Newhall, according to studio manager Daniel Veluzat, and he’s praised the SCV in interviews and conversations with local residents. He really does like it here, said Veluzat, in reference to a question about why Tarantino has filmed his movies at Melody Ranch. “He calls it a special place,” he said. And on Thursday night, “Once Upon a Time” opens in theaters across the country, including the Santa Clarita Valley, featuring scenes shot at both Melody Ranch and the Saugus Speedway. -

The Problem with Borat
Taboo: The Journal of Culture and Education Volume 11 | Issue 1 Article 9 December 2007 The rP oblem with Borat Ghada Chehade Follow this and additional works at: https://digitalcommons.lsu.edu/taboo Recommended Citation Chehade, G. (2017). The rP oblem with Borat. Taboo: The Journal of Culture and Education, 11 (1). https://doi.org/10.31390/ taboo.11.1.09 Taboo, Spring-Summer-Fall-WinterGhada Chehade 2007 63 The Problem with Borat Ghada Chehade There is just something about Borat, Sacha Baron Cohen’s barbaric alter-ego who The Observer’s Oliver Marre (2006) aptly describes as “…homophobic, rac- ist, and misogynist as well as anti-Semitic.” While on the surface, Cohen’s Borat may seem to offend all races equally—the one group he offends the most is the very group he portrays as homophobic, racist, misogynist, and anti-Semitic. Or in other words, the real parties vilified by Cohen are not Borat’s victims but Borat himself. The humour is ultimately directed at this uncivilized buffoon-Borat. He is the butt of every joke. He is the one we laugh at, and are intended to laugh at, the most inasmuch as he is more vulgar, savage, ignorant, barbaric, and racist than any of the bigoted Americans “exposed” in the 2006 film Borat: Cultural Learn- ings of America for Make Benefit Glorious Nation of Kazakhstan. This would not be quite as problematic if the fictional Borat did not come from a very real place and did not so obviously (mis)represent Muslims. While the 2006 film has received coverage and praise for revealing the racism of Americans, very few people are asking whether Cohen’s caricature of a savage, homophobic, misogynist, racist, and hard core Jew-hating Muslim is not actually a form of anti-Muslim racism. -

Actors Anonymous of Legion the Watching from Thrill Different a Be Will That Me, for But, Audience
NOTES FROM THE DREAM FACTORY BY TOM ROSTON he first met when they were both in the 2002 Broadway play Burn This. And although we’re talking about Burrell, Norton might as well be speaking about his own brilliant debut in 1996’s Primal Fear, when he, seemingly out of nowhere, rocketed to recognition. “It is a very particular kind of excitement,” he says. “There is no sense of the artifice. That’s what’s really thrilling.” I am always hoping for pure moments when I watch a movie: those times when my disbelief is so entirely suspended that I forget that I’m watching one. Going into a theater, I often feel overwhelmed with baggage—who the main actor slept with last week, how the director mortgaged his house to get the movie made, and how the production designer only used three shades of green on the set. It even bugs me that once I like a director or an actor, I expect something from him or her, and so the work has an added layer of self-consciousness. When the lights go down, it’s hard to wash the slate entirely clean and just watch. That’s why my eyes tend to drift toward the margins for something surprising. And, often, I see it in an actor whom I know nothing about, and who brings something deeper and richer to his character even though he may have just two minutes of screen time. This may seem random (and that’s the point), but do you remember in the Will Smith movie Hitch, which I just caught on DVD, that there’s this misogynist asshole who is, well, such an asshole? Actor Jeffrey Donovan gets it just right. -

Dragon Con Progress Report 2021 | Published by Dragon Con All Material, Unless Otherwise Noted, Is © 2021 Dragon Con, Inc
WWW.DRAGONCON.ORG INSIDE SEPT. 2 - 6, 2021 • ATLANTA, GEORGIA • WWW.DRAGONCON.ORG Announcements .......................................................................... 2 Guests ................................................................................... 4 Featured Guests .......................................................................... 4 4 FEATURED GUESTS Places to go, things to do, and Attending Pros ......................................................................... 26 people to see! Vendors ....................................................................................... 28 Special 35th Anniversary Insert .......................................... 31 Fan Tracks .................................................................................. 36 Special Events & Contests ............................................... 46 36 FAN TRACKS Art Show ................................................................................... 46 Choose your own adventure with one (or all) of our fan-run tracks. Blood Drive ................................................................................47 Comic & Pop Artist Alley ....................................................... 47 Friday Night Costume Contest ........................................... 48 Hallway Costume Contest .................................................. 48 Puppet Slam ............................................................................ 48 46 SPECIAL EVENTS Moments you won’t want to miss Masquerade Costume Contest ........................................