DOCSLIB.ORG

Table of Integrals Related to Error Function by Nikolai E

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Table of Integrals Related to Error Function by Nikolai E NIKOLAI Е. KOROTKOV Edited by ALEXANDER N. KOROTKOV TABLE OF INTEGRALS RELATED TO ERROR FUNCTION 2019 i Table of integrals related to error function by Nikolai E. Korotkov Retired Leading Researcher, Voronezh Institute of Communications, Russia edited by Alexander N. Korotkov Professor, University of California, Riverside, USA 2019 Nikolai E. Korotkov and Alexander N. Korotkov ii Preface This book presents a table of integrals related to the error function, including indefinite and improper definite integrals. Since many tables of integrals have been published previously and, moreover, computers are widely used nowadays to find integrals numerically and analytically, a natural question is why such a new table would be useful. There are at least three reasons for that. First, to the best of our knowledge, this is the first book (except Russian versions of essentially the same book), which presents a comprehensive collection of integrals related to the error function. Most of the formulas in this book have not been presented in other tables of integrals or have been presented only for some special cases of parameters or for integration only along the real axis of the complex plane. Second, many of the integrals presented here cannot be obtained using a computer (except via an approximate numerical integration). Third, for improper integrals, this book emphasizes the necessary and sufficient conditions for the validity of the presented formulas, including the trajectory for going to infinity on the complex plane; such conditions are usually not given in computer-assisted analytical integration and often not presented in the previously published tables of integrals. We hope that this book will be useful to researchers whose work involves the error function (e.g., via probability integrals in communication theory). It can also be useful to a broader audience. Alexander N. Korotkov and Nikolai E. Korotkov iii CONTENTS Notations and definitions .......................................................................................... 1 Introduction ............................................................................................................... 2 Part 1. Indefinite integrals .......................................................................... 5 1.1. Integrals of the form ∫ z n exp [ (α z + β)2 ] dz ............................................ 5 1.2. Integrals of the form ∫ zn exp ( α22 z +β z +γ) dz ...................................... 7 1.3. Integrals of the form ∫ erf n (α z + β) exp[ −(α z + β)2 ] dz ........................ 8 1.4. Integrals of the form ∫ z n erf (α z + β) exp[ −(α z + β)2 ] dz ...................... 8 1.5. Integrals of the form z n erf (α z + β) exp (β z + γ ) dz ............................. ∫ 1 10 + 1.6. Integrals of the form ∫ z 2m 1 erf (α z + β) exp( α 2 z 2 + γ ) dz .................. 11 2m+1 2 1.7. Integrals of the form ∫ z erf (αz + β)exp(α1 z + γ ) dz ....................... 12 1.8. Integrals of the form ∫ z n erf 2 (α z )exp ( α 2 z 2 )dz .................................. 14 1.9. Integrals of the form ∫ z n erf (α z + β) d z ...................................................... 15 1.10. Integrals of the form ∫ z nerf 2 (α z + β) dz ................................................... 15 2m 1.11. Integrals of the form ∫ z erf (α z ) erf (α1z ) dz ....................................... 17 1.12. Integrals of the form ∫ z 2 m+1erf 3 (α z ) dz ................................................... 18 n m 2 2 1.13. Integrals of the forms ∫ z sin (α z + β z + γ ) dz, ∫ znmsinh (α22 z++ βγ z) dz, n m α 2 2 + β + γ ∫ z cos ( z z ) dz , ∫ znmcosh (α22 z++ βγ z) dz ..................................... 19 n 2 2 1.14. Integrals of the form ∫ z sin (α z + β z + γ )exp (β1 z ) dz ........................ 27 n 2 2 1.15. Integrals of the form ∫ z exp (− α z + β z ) sin (β1 z + γ ) dz ................... 30 iv n −α22 +β α +β +γ 1.16. Integrals of the form ∫ zexp ( z z) sin( 11 z z) dz .............. 33 1.17. Integrals of the form n αβ++ β βγ ............... ∫ zerf( z ) exp( 12z) sin ( z) dz 36 1.18. Integrals of the form 21n+ αβ++ α2 α 2 γ .......... ∫ zerf( z ) exp( 12z) sin ( z) dz 40 Part 2. Definite integrals ............................................................................... 49 2.1. Integrals of z n exp [ (α z + β)2 ] .......................................................... 49 2.2. Integrals of z n exp ( α 2 z 2 + β z + γ )...................................................... 51 2.3. Integrals of erf n (α z + β) exp [− (α z + β)2 ] ......................................... 54 2.4. Integrals of z nerf (α z + β) exp [− (α z + β)2 ] ....................................... 55 n 2.5. Integrals of z erf (α z + β) exp (β1z + γ ) ................................................. 5 8 21m+ 2 2.6. Integrals of zzerf(α + β) exp ( −α1 z) .............................................. 60 n 2 ddddv 2.7. Integrals of zexp(−+α zz β) erf ( αβ11 z +) , vvd n 2 zzexp(−α) erf( αβ11 z ++) erf ( αβ 2 z 2) .................. 63 2.8. Integrals of sin 2m+1 (α 2 z 2 + β z + γ ), sinh2m+ 1(α 22zz++ βγ) , 2m+1 2 2 2m+ 1 22 cos (α z + β z + γ ), cosh (αzz++ βγ) …… 73 n 2 2 2.9. Integrals of z sin (α z + β z + γ )exp (β1 z ) ......................................... 7 7 n 2 2 2 2.10. Integrals of z exp (− α z + β z )sin (α1 z + β1 z + γ ) ........................ 80 n 2.11. Integrals of z erf ( α z + β ) exp ( β1 z ) sin(β 2 z + γ ) .............................. 8 6 2 n+1 2 2 2.12. Integrals of z erf (α z + β) exp(− α1 z )sin (α 2 z + γ ) .................... 89 n 2 2 2.13. Integrals of z erf (α z + β) exp ( −α1 z + β1 z )sin(α 2 z + β 2 z + γ ), n 2 z erf (α z ) exp ( −α1 z )sin(βz ), n 2 z erf (α z ) exp ( −α1 z ) cos(βz ) ........................................... 96 2.14. Integrals of z n [±1− erf (α z + β)], n z [erf (α1 z + β1 ) erf (α 2 z + β 2 )] ................................... 109 v 2.15. Integrals of z n [±1− erf (α z + β)]2 , z n [1− erf 2 (α z + β)] , n (α + β ) 2 (α + β ) z [erf 1 z 1 erf 2 z 2 ], n 22α +β − α +β zzerf ( 11) erf ( 2 z 2) ................................. 114 n 2.16. Integrals of z exp(β z ) [±1 − erf (α z + β1 )], n z exp(β z ) [ erf (α1 z + β1 ) erf (α 2 z + β 2 )] .................. 12 2 n 22 2.17. Integrals of zexp(−α zz +β) ±1 − erf ( α11 z +β) , n 2 2 z exp(− α z + β z )[erf (α1 z + β1 ) erf (α 2 z + β 2 )] .......... 126 n 2 2.18. Integrals of z erf (α z + β1 ) exp [− ( α z + β2 ) ] , n 2 z [±1− erf (α z + β1 )] exp [− ( α z + β2 ) ] , n 2 zzexp(β) erf ( α z +β1 ) , n 2 zzexp(β) 1 − erf ( α z +β1 ) , n β22 α +β − α +β 141 zzexp( ) erf ( 11 z) erf ( 2 z 2) .................. 2 2.19. Integrals of (± 1)nn − erf( αzz +β) exp −( α +β) , 2m+1 3 2m+1 3 z [±1 − erf (α z )] , z [±1 − erf (α z )], 2m+1 3 3 z [erf (α1 z ) erf (α 2 z )] , z 2merf 2 (α z )exp(− α 2 z 2 ), z 2m [1 − erf 2 (α z )]exp( − α 2 z 2 ) ............................................ 15 9 2.20. Integrals of z n sin (β z + γ )[±1− erf (α z + β )], 1 n z sin (β z + γ )[erf (α1z + β1 ) erf (α 2 z + β 2 )], n 2 zsin (α zz +β+γ±−)1 erf ( α11 z +β) , n 2 163 zsin (α zz +β+γ)erf ( α+β11 z) erf ( α 2 z +β 2) ........... Appendix. Some useful formulas for obtaining other integrals .......................... 177 vi NOTATIONS and DEFINITIONS θ 2 erf (θ= )∫ exp( −z2 ) dz is the error function (probability integral). π 0 θ 2 erfi(θ= )∫ exp(z2 ) dz=− i erf ( i θ ) is the imaginary error function. π 0 m, n, k, l, r, q are nonnegative integers (0, 1, 2, …). a, b, c are real numbers. α, β, γ, µ, ν, θ are complex numbers (can be real as well). x is a real integration variable. z is a complex integration variable (can be real as well). i is the imaginary unit. π and e have their usual meaning. Reθ and Imθ are real and imaginary parts of θ , θ = Re θ + i Imθ. θ= Reθ − i Im θ is the complex conjugate of θ . θ = Re 2 θ + Im 2 θ is the absolute value of θ . arg θ is the argument of a complex number θ , −<ππarg θ ≤ . ∞ is the infinity symbol used on the complex plane. − ∞ and + ∞ are the infinity symbols for real numbers (or the real axis). θ → ∞(T ) means θ goes to infinity on the complex plane along trajectory T . n ∑ θk denotes summation; equals 0 if n < m . k =m m! is the factorial of m (with usual convention 0!1!1= = ). E (c) is the integer part (floor function) of a real number c. ∞ ()T2 ∫ ϕ()z dz is an improper integral on the complex plane with trajectories ∞ ()T1 T1 and T2 both going to infinity. lnθ= ln θ +i arg θ is the principal value of natural logarithm. 11+θi arctanθ= arctg θ= atan θ= ln is the principal value of inverse tangent. 21ii−θ 1 INTRODUCTION Formulas in this book are numbered by part, section, subsection, and formula number. When a formula is too long, it is written in terms of abbreviated expressions, which are listed at the ends of sections. Most of the presented formulas assume complex parameters and integration on the complex plane.
Load more

Recommended publications
  • 18.01A Topic 5: Second Fundamental Theorem, Lnx As an Integral. Read
    18.01A Topic 5: Second fundamental theorem, ln x as an integral. Read: SN: PI, FT. 0 R b b First Fundamental Theorem: F = f ⇒ a f(x) dx = F (x)|a Questions: 1. Why dx? 2. Given f(x) does F (x) always exist? Answer to question 1. Pn R b a) Riemann sum: Area ≈ 1 f(ci)∆x → a f(x) dx In the limit the sum becomes an integral and the finite ∆x becomes the infinitesimal dx. b) The dx helps with change of variable. a b 1 Example: Compute R √ 1 dx. 0 1−x2 Let x = sin u. dx du = cos u ⇒ dx = cos u du, x = 0 ⇒ u = 0, x = 1 ⇒ u = π/2. 1 π/2 π/2 π/2 R √ 1 R √ 1 R cos u R Substituting: 2 dx = cos u du = du = du = π/2. 0 1−x 0 1−sin2 u 0 cos u 0 Answer to question 2. Yes → Second Fundamental Theorem: Z x If f is continuous and F (x) = f(u) du then F 0(x) = f(x). a I.e. f always has an anit-derivative. This is subtle: we have defined a NEW function F (x) using the definite integral. Note we needed a dummy variable u for integration because x was already taken. Z x+∆x f(x) proof: ∆area = f(x) dx 44 4 x Z x+∆x Z x o area = ∆F = f(x) dx − f(x) dx 0 0 = F (x + ∆x) − F (x) = ∆F. x x + ∆x ∆F But, also ∆area ≈ f(x) ∆x ⇒ ∆F ≈ f(x) ∆x or ≈ f(x).
    [Show full text]
  • The Enigmatic Number E: a History in Verse and Its Uses in the Mathematics Classroom
    To appear in MAA Loci: Convergence The Enigmatic Number e: A History in Verse and Its Uses in the Mathematics Classroom Sarah Glaz Department of Mathematics University of Connecticut Storrs, CT 06269 [email protected] Introduction In this article we present a history of e in verse—an annotated poem: The Enigmatic Number e . The annotation consists of hyperlinks leading to biographies of the mathematicians appearing in the poem, and to explanations of the mathematical notions and ideas presented in the poem. The intention is to celebrate the history of this venerable number in verse, and to put the mathematical ideas connected with it in historical and artistic context. The poem may also be used by educators in any mathematics course in which the number e appears, and those are as varied as e's multifaceted history. The sections following the poem provide suggestions and resources for the use of the poem as a pedagogical tool in a variety of mathematics courses. They also place these suggestions in the context of other efforts made by educators in this direction by briefly outlining the uses of historical mathematical poems for teaching mathematics at high-school and college level. Historical Background The number e is a newcomer to the mathematical pantheon of numbers denoted by letters: it made several indirect appearances in the 17 th and 18 th centuries, and acquired its letter designation only in 1731. Our history of e starts with John Napier (1550-1617) who defined logarithms through a process called dynamical analogy [1]. Napier aimed to simplify multiplication (and in the same time also simplify division and exponentiation), by finding a model which transforms multiplication into addition.
    [Show full text]
  • MATH 305 Complex Analysis, Spring 2016 Using Residues to Evaluate Improper Integrals Worksheet for Sections 78 and 79
    MATH 305 Complex Analysis, Spring 2016 Using Residues to Evaluate Improper Integrals Worksheet for Sections 78 and 79 One of the interesting applications of Cauchy's Residue Theorem is to find exact values of real improper integrals. The idea is to integrate a complex rational function around a closed contour C that can be arbitrarily large. As the size of the contour becomes infinite, the piece in the complex plane (typically an arc of a circle) contributes 0 to the integral, while the part remaining covers the entire real axis (e.g., an improper integral from −∞ to 1). An Example Let us use residues to derive the formula p Z 1 x2 2 π 4 dx = : (1) 0 x + 1 4 Note the somewhat surprising appearance of π for the value of this integral. z2 First, let f(z) = and let C = L + C be the contour that consists of the line segment L z4 + 1 R R R on the real axis from −R to R, followed by the semi-circle CR of radius R traversed CCW (see figure below). Note that C is a positively oriented, simple, closed contour. We will assume that R > 1. Next, notice that f(z) has two singular points (simple poles) inside C. Call them z0 and z1, as shown in the figure. By Cauchy's Residue Theorem. we have I f(z) dz = 2πi Res f(z) + Res f(z) C z=z0 z=z1 On the other hand, we can parametrize the line segment LR by z = x; −R ≤ x ≤ R, so that I Z R x2 Z z2 f(z) dz = 4 dx + 4 dz; C −R x + 1 CR z + 1 since C = LR + CR.
    [Show full text]
  • Section 8.8: Improper Integrals
    Section 8.8: Improper Integrals One of the main applications of integrals is to compute the areas under curves, as you know. A geometric question. But there are some geometric questions which we do not yet know how to do by calculus, even though they appear to have the same form. Consider the curve y = 1=x2. We can ask, what is the area of the region under the curve and right of the line x = 1? We have no reason to believe this area is finite, but let's ask. Now no integral will compute this{we have to integrate over a bounded interval. Nonetheless, we don't want to throw up our hands. So note that b 2 b Z (1=x )dx = ( 1=x) 1 = 1 1=b: 1 − j − In other words, as b gets larger and larger, the area under the curve and above [1; b] gets larger and larger; but note that it gets closer and closer to 1. Thus, our intuition tells us that the area of the region we're interested in is exactly 1. More formally: lim 1 1=b = 1: b − !1 We can rewrite that as b 2 lim Z (1=x )dx: b !1 1 Indeed, in general, if we want to compute the area under y = f(x) and right of the line x = a, we are computing b lim Z f(x)dx: b !1 a ASK: Does this limit always exist? Give some situations where it does not exist. They'll give something that blows up.
    [Show full text]
  • The Error Function Mathematical Physics
    R. I. Badran The Error Function Mathematical Physics The Error Function and Stirling’s Formula The Error Function: x 2 The curve of the Gaussian function y e is called the bell-shaped graph. The error function is defined as the area under part of this curve: x 2 2 erf (x) et dt 1. . 0 There are other definitions of error functions. These are closely related integrals to the above one. 2. a) The normal or Gaussian distribution function. x t2 1 1 1 x P(, x) e 2 dt erf ( ) 2 2 2 2 Proof: Put t 2u and proceed, you might reach a step of x 1 2 P(0, x) eu du P(,x) P(,0) P(0,x) , where 0 1 x P(0, x) erf ( ) Here you can prove that 2 2 . This can be done by using the definition of error function in (1). 0 u2 I I e du Now you need to find P(,0) where . To find this integral you have to put u=x first, then u= y and multiply the two resulting integrals. Make the change of variables to polar coordinate you get R. I. Badran The Error Function Mathematical Physics 0 2 2 I 2 er rdr d 0 From this latter integral you get 1 I P(,0) 2 and 2 . 1 1 x P(, x) erf ( ) 2 2 2 Q. E. D. x 2 t 1 2 1 x 2.b P(0, x) e dt erf ( ) 2 0 2 2 (as proved earlier in 2.a).
    [Show full text]
  • Applications of the Exponential and Natural Logarithm Functions
    M06_GOLD7774_14_SE_C05.indd Page 254 09/11/16 7:31 PM localadmin /202/AW00221/9780134437774_GOLDSTEIN/GOLDSTEIN_CALCULUS_AND_ITS_APPLICATIONS_14E1 ... FOR REVIEW BY POTENTIAL ADOPTERS ONLY chapter 5SAMPLE Applications of the Exponential and Natural Logarithm Functions 5.1 Exponential Growth and Decay 5.4 Further Exponential Models 5.2 Compound Interest 5.3 Applications of the Natural Logarithm Function to Economics n Chapter 4, we introduced the exponential function y = ex and the natural logarithm Ifunction y = ln x, and we studied their most important properties. It is by no means clear that these functions have any substantial connection with the physical world. How- ever, as this chapter will demonstrate, the exponential and natural logarithm functions are involved in the study of many physical problems, often in a very curious and unex- pected way. 5.1 Exponential Growth and Decay Exponential Growth You walk into your kitchen one day and you notice that the overripe bananas that you left on the counter invited unwanted guests: fruit flies. To take advantage of this pesky situation, you decide to study the growth of the fruit flies colony. It didn’t take you too FOR REVIEW long to make your first observation: The colony is increasing at a rate that is propor- tional to its size. That is, the more fruit flies, the faster their number grows. “The derivative is a rate To help us model this population growth, we introduce some notation. Let P(t) of change.” See Sec. 1.7, denote the number of fruit flies in your kitchen, t days from the moment you first p.
    [Show full text]
  • Math 1B, Lecture 11: Improper Integrals I
    Math 1B, lecture 11: Improper integrals I Nathan Pflueger 30 September 2011 1 Introduction An improper integral is an integral that is unbounded in one of two ways: either the domain of integration is infinite, or the function approaches infinity in the domain (or both). Conceptually, they are no different from ordinary integrals (and indeed, for many students including myself, it is not at all clear at first why they have a special name and are treated as a separate topic). Like any other integral, an improper integral computes the area underneath a curve. The difference is foundational: if integrals are defined in terms of Riemann sums which divide the domain of integration into n equal pieces, what are we to make of an integral with an infinite domain of integration? The purpose of these next two lecture will be to settle on the appropriate foundation for speaking of improper integrals. Today we consider integrals with infinite domains of integration; next time we will consider functions which approach infinity in the domain of integration. An important observation is that not all improper integrals can be considered to have meaningful values. These will be said to diverge, while the improper integrals with coherent values will be said to converge. Much of our work will consist in understanding which improper integrals converge or diverge. Indeed, in many cases for this course, we will only ask the question: \does this improper integral converge or diverge?" The reading for today is the first part of Gottlieb x29:4 (up to the top of page 907).
    [Show full text]
  • Error Functions
    Error functions Nikolai G. Lehtinen April 23, 2010 1 Error function erf x and complementary er- ror function erfc x (Gauss) error function is 2 x 2 erf x = e−t dt (1) √π Z0 and has properties erf ( )= 1, erf (+ ) = 1 −∞ − ∞ erf ( x)= erf (x), erf (x∗) = [erf(x)]∗ − − where the asterisk denotes complex conjugation. Complementary error function is defined as ∞ 2 2 erfc x = e−t dt = 1 erf x (2) √π Zx − Note also that 2 x 2 e−t dt = 1 + erf x −∞ √π Z Another useful formula: 2 x − t π x e 2σ2 dt = σ erf Z0 r 2 "√2σ # Some Russian authors (e.g., Mikhailovskiy, 1975; Bogdanov et al., 1976) call erf x a Cramp function. 1 2 Faddeeva function w(x) Faddeeva (or Fadeeva) function w(x)(Fadeeva and Terent’ev, 1954; Poppe and Wijers, 1990) does not have a name in Abramowitz and Stegun (1965, ch. 7). It is also called complex error function (or probability integral)(Weide- man, 1994; Baumjohann and Treumann, 1997, p. 310) or plasma dispersion function (Weideman, 1994). To avoid confusion, we will reserve the last name for Z(x), see below. Some Russian authors (e.g., Mikhailovskiy, 1975; Bogdanov et al., 1976) call it a (complex) Cramp function and denote as W (x). Faddeeva function is defined as 2 2i x 2 2 2 w(x)= e−x 1+ et dt = e−x [1+erf(ix)] = e−x erfc ( ix) (3) √π Z0 ! − Integral representations: 2 2 i ∞ e−t dt 2ix ∞ e−t dt w(x)= = (4) π −∞ x t π 0 x2 t2 Z − Z − where x> 0.
    [Show full text]
  • Global Minimax Approximations and Bounds for the Gaussian Q-Functionbysumsofexponentials 3
    IEEE TRANSACTIONS ON COMMUNICATIONS 1 Global Minimax Approximations and Bounds for the Gaussian Q-Function by Sums of Exponentials Islam M. Tanash and Taneli Riihonen , Member, IEEE Abstract—This paper presents a novel systematic methodology The Gaussian Q-function has many applications in statis- to obtain new simple and tight approximations, lower bounds, tical performance analysis such as evaluating bit, symbol, and upper bounds for the Gaussian Q-function, and functions and block error probabilities for various digital modulation thereof, in the form of a weighted sum of exponential functions. They are based on minimizing the maximum absolute or relative schemes and different fading models [5]–[11], and evaluat- error, resulting in globally uniform error functions with equalized ing the performance of energy detectors for cognitive radio extrema. In particular, we construct sets of equations that applications [12], [13], whenever noise and interference or describe the behaviour of the targeted error functions and a channel can be modelled as a Gaussian random variable. solve them numerically in order to find the optimized sets of However, in many cases formulating such probabilities will coefficients for the sum of exponentials. This also allows for establishing a trade-off between absolute and relative error by result in complicated integrals of the Q-function that cannot controlling weights assigned to the error functions’ extrema. We be expressed in a closed form in terms of elementary functions. further extend the proposed procedure to derive approximations Therefore, finding tractable approximations and bounds for and bounds for any polynomial of the Q-function, which in the Q-function becomes a necessity in order to facilitate turn allows approximating and bounding many functions of the expression manipulations and enable its application over a Q-function that meet the Taylor series conditions, and consider the integer powers of the Q-function as a special case.
    [Show full text]
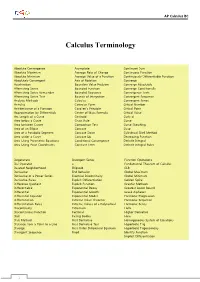
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Approximation of Logarithm, Factorial and Euler- Mascheroni Constant Using Odd Harmonic Series
    Mathematical Forum ISSN: 0972-9852 Vol.28(2), 2020 APPROXIMATION OF LOGARITHM, FACTORIAL AND EULER- MASCHERONI CONSTANT USING ODD HARMONIC SERIES Narinder Kumar Wadhawan1and Priyanka Wadhawan2 1Civil Servant,Indian Administrative Service Now Retired, House No.563, Sector 2, Panchkula-134112, India 2Department Of Computer Sciences, Thapar Institute Of Engineering And Technology, Patiala-144704, India, now Program Manager- Space Management (TCS) Walgreen Co. 304 Wilmer Road, Deerfield, Il. 600015 USA, Email :[email protected],[email protected] Received on: 24/09/ 2020 Accepted on: 16/02/ 2021 Abstract We have proved in this paper that natural logarithm of consecutive numbers ratio, x/(x-1) approximatesto 2/(2x - 1) where x is a real number except 1. Using this relation, we, then proved, x approximates to double the sum of odd harmonic series having first and last terms 1/3 and 1/(2x - 1) respectively. Thereafter, not limiting to consecutive numbers ratios, we extended its applicability to all the real numbers. Based on these relations, we, then derived a formula for approximating the value of Factorial x.We could also approximate the value of Euler-Mascheroni constant. In these derivations, we used only and only elementary functions, thus this paper is easily comprehensible to students and scholars alike. Keywords:Numbers, Approximation, Building Blocks, Consecutive Numbers Ratios, NaturalLogarithm, Factorial, Euler Mascheroni Constant, Odd Numbers Harmonic Series. 2010 AMS classification:Number Theory 11J68, 11B65, 11Y60 125 Narinder Kumar Wadhawan and Priyanka Wadhawan 1. Introduction By applying geometric approach, Leonhard Euler, in the year 1748, devised methods of determining natural logarithm of a number [2].
    [Show full text]
  • Section 7.2, Integration by Parts
    Section 7.2, Integration by Parts Homework: 7.2 #1{57 odd 2 So far, we have been able to integrate some products, such as R xex dx. They have been able to be solved by a u-substitution. However, what happens if we can't solve it by a u-substitution? For example, consider R xex dx. For this, we will need a technique called integration by parts. 0 0 From the product rule for derivatives, we know that Dx[u(x)v(x)] = u (x)v(x) + u(x)v (x). Rear- ranging this and integrating, we see that: 0 0 u(x)v (x) = Dx[u(x)v(x)] − u (x)v(x) Z Z Z 0 0 u(x)v (x) dx = Dx[u(x)v(x)] dx − u (x)v(x) dx This gives us the formula needed for integration by parts: Z Z u(x)v0(x) dx = u(x)v(x) − u0(x)v(x) dx; or, we can write it as Z Z u dv = uv − v du In this section, we will practice choosing u and v properly. Examples Perform each of the following integrations: 1. R xex dx Let u = x, and dv = ex dx. Then, du = dx and v = ex. Using our formula, we get that Z Z xex dx = xex − ex dx = xex − ex + C R lnpx 2. x dx Since we do not know how to integrate ln x, let u = ln x and dv = x−1=2. Then du = 1=x and v = 2x1=2, so Z ln x Z p dx = 2x1=2 ln x − 2x−1=2 dx x = 2x1=2 ln x − 4x1=2 + C 3.
    [Show full text]