Calculation Reference Handout Written by Chris and Mehran Sahami
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

18.01A Topic 5: Second Fundamental Theorem, Lnx As an Integral. Read
18.01A Topic 5: Second fundamental theorem, ln x as an integral. Read: SN: PI, FT. 0 R b b First Fundamental Theorem: F = f ⇒ a f(x) dx = F (x)|a Questions: 1. Why dx? 2. Given f(x) does F (x) always exist? Answer to question 1. Pn R b a) Riemann sum: Area ≈ 1 f(ci)∆x → a f(x) dx In the limit the sum becomes an integral and the finite ∆x becomes the infinitesimal dx. b) The dx helps with change of variable. a b 1 Example: Compute R √ 1 dx. 0 1−x2 Let x = sin u. dx du = cos u ⇒ dx = cos u du, x = 0 ⇒ u = 0, x = 1 ⇒ u = π/2. 1 π/2 π/2 π/2 R √ 1 R √ 1 R cos u R Substituting: 2 dx = cos u du = du = du = π/2. 0 1−x 0 1−sin2 u 0 cos u 0 Answer to question 2. Yes → Second Fundamental Theorem: Z x If f is continuous and F (x) = f(u) du then F 0(x) = f(x). a I.e. f always has an anit-derivative. This is subtle: we have defined a NEW function F (x) using the definite integral. Note we needed a dummy variable u for integration because x was already taken. Z x+∆x f(x) proof: ∆area = f(x) dx 44 4 x Z x+∆x Z x o area = ∆F = f(x) dx − f(x) dx 0 0 = F (x + ∆x) − F (x) = ∆F. x x + ∆x ∆F But, also ∆area ≈ f(x) ∆x ⇒ ∆F ≈ f(x) ∆x or ≈ f(x). -

The Enigmatic Number E: a History in Verse and Its Uses in the Mathematics Classroom
To appear in MAA Loci: Convergence The Enigmatic Number e: A History in Verse and Its Uses in the Mathematics Classroom Sarah Glaz Department of Mathematics University of Connecticut Storrs, CT 06269 [email protected] Introduction In this article we present a history of e in verse—an annotated poem: The Enigmatic Number e . The annotation consists of hyperlinks leading to biographies of the mathematicians appearing in the poem, and to explanations of the mathematical notions and ideas presented in the poem. The intention is to celebrate the history of this venerable number in verse, and to put the mathematical ideas connected with it in historical and artistic context. The poem may also be used by educators in any mathematics course in which the number e appears, and those are as varied as e's multifaceted history. The sections following the poem provide suggestions and resources for the use of the poem as a pedagogical tool in a variety of mathematics courses. They also place these suggestions in the context of other efforts made by educators in this direction by briefly outlining the uses of historical mathematical poems for teaching mathematics at high-school and college level. Historical Background The number e is a newcomer to the mathematical pantheon of numbers denoted by letters: it made several indirect appearances in the 17 th and 18 th centuries, and acquired its letter designation only in 1731. Our history of e starts with John Napier (1550-1617) who defined logarithms through a process called dynamical analogy [1]. Napier aimed to simplify multiplication (and in the same time also simplify division and exponentiation), by finding a model which transforms multiplication into addition. -

Applications of the Exponential and Natural Logarithm Functions
M06_GOLD7774_14_SE_C05.indd Page 254 09/11/16 7:31 PM localadmin /202/AW00221/9780134437774_GOLDSTEIN/GOLDSTEIN_CALCULUS_AND_ITS_APPLICATIONS_14E1 ... FOR REVIEW BY POTENTIAL ADOPTERS ONLY chapter 5SAMPLE Applications of the Exponential and Natural Logarithm Functions 5.1 Exponential Growth and Decay 5.4 Further Exponential Models 5.2 Compound Interest 5.3 Applications of the Natural Logarithm Function to Economics n Chapter 4, we introduced the exponential function y = ex and the natural logarithm Ifunction y = ln x, and we studied their most important properties. It is by no means clear that these functions have any substantial connection with the physical world. How- ever, as this chapter will demonstrate, the exponential and natural logarithm functions are involved in the study of many physical problems, often in a very curious and unex- pected way. 5.1 Exponential Growth and Decay Exponential Growth You walk into your kitchen one day and you notice that the overripe bananas that you left on the counter invited unwanted guests: fruit flies. To take advantage of this pesky situation, you decide to study the growth of the fruit flies colony. It didn’t take you too FOR REVIEW long to make your first observation: The colony is increasing at a rate that is propor- tional to its size. That is, the more fruit flies, the faster their number grows. “The derivative is a rate To help us model this population growth, we introduce some notation. Let P(t) of change.” See Sec. 1.7, denote the number of fruit flies in your kitchen, t days from the moment you first p. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential -

Approximation of Logarithm, Factorial and Euler- Mascheroni Constant Using Odd Harmonic Series
Mathematical Forum ISSN: 0972-9852 Vol.28(2), 2020 APPROXIMATION OF LOGARITHM, FACTORIAL AND EULER- MASCHERONI CONSTANT USING ODD HARMONIC SERIES Narinder Kumar Wadhawan1and Priyanka Wadhawan2 1Civil Servant,Indian Administrative Service Now Retired, House No.563, Sector 2, Panchkula-134112, India 2Department Of Computer Sciences, Thapar Institute Of Engineering And Technology, Patiala-144704, India, now Program Manager- Space Management (TCS) Walgreen Co. 304 Wilmer Road, Deerfield, Il. 600015 USA, Email :[email protected],[email protected] Received on: 24/09/ 2020 Accepted on: 16/02/ 2021 Abstract We have proved in this paper that natural logarithm of consecutive numbers ratio, x/(x-1) approximatesto 2/(2x - 1) where x is a real number except 1. Using this relation, we, then proved, x approximates to double the sum of odd harmonic series having first and last terms 1/3 and 1/(2x - 1) respectively. Thereafter, not limiting to consecutive numbers ratios, we extended its applicability to all the real numbers. Based on these relations, we, then derived a formula for approximating the value of Factorial x.We could also approximate the value of Euler-Mascheroni constant. In these derivations, we used only and only elementary functions, thus this paper is easily comprehensible to students and scholars alike. Keywords:Numbers, Approximation, Building Blocks, Consecutive Numbers Ratios, NaturalLogarithm, Factorial, Euler Mascheroni Constant, Odd Numbers Harmonic Series. 2010 AMS classification:Number Theory 11J68, 11B65, 11Y60 125 Narinder Kumar Wadhawan and Priyanka Wadhawan 1. Introduction By applying geometric approach, Leonhard Euler, in the year 1748, devised methods of determining natural logarithm of a number [2]. -

Section 7.2, Integration by Parts
Section 7.2, Integration by Parts Homework: 7.2 #1{57 odd 2 So far, we have been able to integrate some products, such as R xex dx. They have been able to be solved by a u-substitution. However, what happens if we can't solve it by a u-substitution? For example, consider R xex dx. For this, we will need a technique called integration by parts. 0 0 From the product rule for derivatives, we know that Dx[u(x)v(x)] = u (x)v(x) + u(x)v (x). Rear- ranging this and integrating, we see that: 0 0 u(x)v (x) = Dx[u(x)v(x)] − u (x)v(x) Z Z Z 0 0 u(x)v (x) dx = Dx[u(x)v(x)] dx − u (x)v(x) dx This gives us the formula needed for integration by parts: Z Z u(x)v0(x) dx = u(x)v(x) − u0(x)v(x) dx; or, we can write it as Z Z u dv = uv − v du In this section, we will practice choosing u and v properly. Examples Perform each of the following integrations: 1. R xex dx Let u = x, and dv = ex dx. Then, du = dx and v = ex. Using our formula, we get that Z Z xex dx = xex − ex dx = xex − ex + C R lnpx 2. x dx Since we do not know how to integrate ln x, let u = ln x and dv = x−1=2. Then du = 1=x and v = 2x1=2, so Z ln x Z p dx = 2x1=2 ln x − 2x−1=2 dx x = 2x1=2 ln x − 4x1=2 + C 3. -

The Logarithmic Chicken Or the Exponential Egg: Which Comes First?
The Logarithmic Chicken or the Exponential Egg: Which Comes First? Marshall Ransom, Senior Lecturer, Department of Mathematical Sciences, Georgia Southern University Dr. Charles Garner, Mathematics Instructor, Department of Mathematics, Rockdale Magnet School Laurel Holmes, 2017 Graduate of Rockdale Magnet School, Current Student at University of Alabama Background: This article arose from conversations between the first two authors. In discussing the functions ln(x) and ex in introductory calculus, one of us made good use of the inverse function properties and the other had a desire to introduce the natural logarithm without the classic definition of same as an integral. It is important to introduce mathematical topics using a minimal number of definitions and postulates/axioms when results can be derived from existing definitions and postulates/axioms. These are two of the ideas motivating the article. Thus motivated, the authors compared manners with which to begin discussion of the natural logarithm and exponential functions in a calculus class. x A related issue is the use of an integral to define a function g in terms of an integral such as g()() x f t dt . c We believe that this is something that students should understand and be exposed to prior to more advanced x x sin(t ) 1 “surprises” such as Si(x ) dt . In particular, the fact that ln(x ) dt is extremely important. But t t 0 1 must that fact be introduced as a definition? Can the natural logarithm function arise in an introductory calculus x 1 course without the -
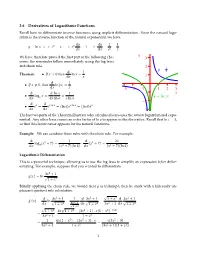
3.6 Derivatives of Logarithmic Functions Y = Ln X ⇐⇒ Ey = X =⇒ Ey
3.6 Derivatives of Logarithmic Functions Recall how to differentiate inverse functions using implicit differentiation. Since the natural loga- rithm is the inverse function of the natural exponential, we have dy dy 1 1 y = ln x ey = x = ey = 1 = = = () ) dx ) dx ey x y We have therefore proved the first part of the following The- 3 orem: the remainder follow immediately using the log laws and chain rule. 2 y = 1 d 1 x Theorem. If x > 0 then ln x = • dx x 1 d 1 If x = 0, then ln x = • 6 dx j j x 3 2 1123 − − − d d ln x 1 1 x log x = = − y = ln x • dx a dx ln a x ln a | | 2 d d − ax = ex ln a = (ln a)ex ln a = (ln a)ax • dx dx 3 − The last two parts of the Theorem illustrate why calculus always uses the natural logarithm and expo- nential. Any other base causes an extra factor of ln a to appear in the derivative. Recall that ln e = 1, so that this factor never appears for the natural functions. Example We can combine these rules with the chain rule. For example: d 1 d 2x log (x2 + 7) = (x2 + 7) = dx 4 (x2 + 7)(ln 4) · dx (x2 + 7)(ln 4) Logarithmic Differentiation This is a powerful technique, allowing us to use the log laws to simplify an expression before differ- entiating. For example, suppose that you wanted to differentiate 3x2 + 1 g(x) = ln p1 + x2 Blindly applying the chain rule, we would treat g as ln(lump), then be stuck with a hideously un- pleasant quotient rule calculation: d 3x2 + 1 1 d 3x2 + 1 p1 + x2 d 3x2 + 1 g0(x) = ln = 2 = dx p1 + x2 3x +1 dx p1 + x2 3x2 + 1 dx p1 + x2 p1+x2 p1 + x2 6xp1 + x2 (3x2 + 1) x(1 + x2) 1/2 = − · − 3x2 + 1 · 1 + x2 1 6x(1 + x2) (3x2 + 1) x x(3x2 + 5) = − · = 3x2 + 1 · 1 + x2 (3x2 + 1)(1 + x2) 1 Thankfully there is a better way: apply the logarithm laws first, 3x2 + 1 1 g(x) = ln = ln(3x2 + 1) ln(1 + x2) p1 + x2 − 2 and then differentiate: 1 d 2 1 d 2 g0(x) = (3x + 1) (1 + x ) 3x2 + 1 dx − 2(1 + x2) dx 6x x = 3x2 + 1 − 1 + x2 A little algebra shows that we have the same solution, in a much simpler way. -

Chapter 8 Logarithms and Exponentials: Logx and E
Chapter 8 Logarithms and Exponentials: log x and ex These two functions are ones with which you already have some familiarity. Both are in- troduced in many high school curricula, as they have widespread applications in both the scientific and financial worlds. In fact, as recently as 50 years ago, many high school math- ematics curricula included considerable study of “Tables of the Logarithm Function” (“log tables”), because this was prior to the invention of the hand-held calculator. During the Great Depression of the 1930’s, many out-of-work mathematicians and scientists were em- ployed as “calculators” or “computers” to develop these tables by hand, laboriously using difference equations, entry by entry! Here, we are going to use our knowledge of the Fun- damental Theorem of Calculus and the Inverse Function Theorem to develop the properties of the Logarithm Function and Exponential Function. Of course, we don’t need tables of these functions any more because it is possible to buy a hand-held electronic calculator for as little as $10.00, which will compute any value of these functions to 10 decimal places or more! 1 2 CHAPTER 8. LOGARITHMS AND EXPONENTIALS: LOG X AND EX 8.1 The Logarithm Function Define log(x) (which we shall be thinking of as the natural logarithm) by the following: Definition 8.1 x 1 log(x)= dt for x>0. 1 t Theorem 8.1 log x is defined for all x>0. It is everywhere differentiable, hence continuous, and is a 1-1 function. The Range of log x is (−∞, ∞). -

The Indefinite Logarithm, Logarithmic Units, and the Nature of Entropy
The Indefinite Logarithm, Logarithmic Units, and the Nature of Entropy Michael P. Frank FAMU-FSU College of Engineering Dept. of Electrical & Computer Engineering 2525 Pottsdamer St., Rm. 341 Tallahassee, FL 32310 [email protected] August 20, 2017 Abstract We define the indefinite logarithm [log x] of a real number x> 0 to be a mathematical object representing the abstract concept of the logarithm of x with an indeterminate base (i.e., not specifically e, 10, 2, or any fixed number). The resulting indefinite logarithmic quantities naturally play a mathematical role that is closely analogous to that of dimensional physi- cal quantities (such as length) in that, although these quantities have no definite interpretation as ordinary numbers, nevertheless the ratio of two of these entities is naturally well-defined as a specific, ordinary number, just like the ratio of two lengths. As a result, indefinite logarithm objects can serve as the basis for logarithmic spaces, which are natural systems of logarithmic units suitable for measuring any quantity defined on a log- arithmic scale. We illustrate how logarithmic units provide a convenient language for explaining the complete conceptual unification of the dis- parate systems of units that are presently used for a variety of quantities that are conventionally considered distinct, such as, in particular, physical entropy and information-theoretic entropy. 1 Introduction The goal of this paper is to help clear up what is perceived to be a widespread arXiv:physics/0506128v1 [physics.gen-ph] 15 Jun 2005 confusion that can found in many popular sources (websites, popular books, etc.) regarding the proper mathematical status of a variety of physical quantities that are conventionally defined on logarithmic scales. -

Section 3.2. the Natural Logarithm Function
3.2. THE NATURAL LOGARITHM FUNCTION 137 3.2 The natural logarithm function We further examine some exponential growth/decay contexts considered in Section 3.1, and de- velop some tools to solve certain kinds of problems that arise in those contexts. Solving the equation ea = b In Section 3.1, we solved exponential growth and decay problems problems of the “how large/how much” variety. That is: using formulas like kt kt P = P0e and R = R0e− , (3.2.1) we were able to answer some questions like “how large is this population after that many years,” or “how much of this radioactive substance is left after that many hours?” Answers to such problems entail simply putting the appropriate value of t into the appropriate formula (3.2.1) for the exponentially growing/decaying substance. What we have not yet considered are answers to “how long” questions, in exponential growth/decay situations. That is, how do we solve equations like (3.2.1) for t,givenvaluesoftheothervariables and constants involved? For example, consider the following. Example 3.2.1. Suppose a population, initially comprising 100,000 persons, is growing at the per capita rate of k = 3birthsperthousandpersonsperyear. (a) Write down an initial value problem modeling this situation. (b) How large will this population be 37 years from now? (c) How long will it take the population to double? Solution. (a) Denoting time in months by t,andpopulationinindividualsbyP (t),wehavethe initial value problem P 0(t)=0.003P (t); P (0) = 100,000. (b) Using the results of Section 3.1, we know that the solution to the problem is the exponential function P (t)=100,000 e0.003t. -

Leonhard Euler English Version
LEONHARD EULER (April 15, 1707 – September 18, 1783) by HEINZ KLAUS STRICK , Germany Without a doubt, LEONHARD EULER was the most productive mathematician of all time. He wrote numerous books and countless articles covering a vast range of topics in pure and applied mathematics, physics, astronomy, geodesy, cartography, music, and shipbuilding – in Latin, French, Russian, and German. It is not only that he produced an enormous body of work; with unbelievable creativity, he brought innovative ideas to every topic on which he wrote and indeed opened up several new areas of mathematics. Pictured on the Swiss postage stamp of 2007 next to the polyhedron from DÜRER ’s Melencolia and EULER ’s polyhedral formula is a portrait of EULER from the year 1753, in which one can see that he was already suffering from eye problems at a relatively young age. EULER was born in Basel, the son of a pastor in the Reformed Church. His mother also came from a family of pastors. Since the local school was unable to provide an education commensurate with his son’s abilities, EULER ’s father took over the boy’s education. At the age of 14, EULER entered the University of Basel, where he studied philosophy. He completed his studies with a thesis comparing the philosophies of DESCARTES and NEWTON . At 16, at his father’s wish, he took up theological studies, but he switched to mathematics after JOHANN BERNOULLI , a friend of his father’s, convinced the latter that LEONHARD possessed an extraordinary mathematical talent. At 19, EULER won second prize in a competition sponsored by the French Academy of Sciences with a contribution on the question of the optimal placement of a ship’s masts (first prize was awarded to PIERRE BOUGUER , participant in an expedition of LA CONDAMINE to South America).