DOCSLIB.ORG

PROPT - Matlab Optimal Control Software

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
PROPT - Matlab Optimal Control Software PROPT - Matlab Optimal Control Software - ONE OF A KIND, LIGHTNING FAST SOLUTIONS TO YOUR OPTIMAL CONTROL PROBLEMS! Per E. Rutquist1 and Marcus M. Edvall2 April 26, 2010 1Tomlab Optimization AB, V¨aster˚asTechnology Park, Trefasgatan 4, SE-721 30 V¨aster˚as,Sweden. 2Tomlab Optimization Inc., 1260 SE Bishop Blvd Ste E, Pullman, WA, USA. 1 Contents Contents 2 1 PROPT Guide Overview 22 1.1 Installation................................................. 22 1.2 Foreword to the software.......................................... 22 1.3 Initial remarks............................................... 22 2 Introduction to PROPT 24 2.1 Overview of PROPT syntax........................................ 24 2.2 Vector representation........................................... 25 2.3 Global optimality............................................. 25 3 Modeling optimal control problems 27 3.1 A simple example.............................................. 27 3.2 Code generation.............................................. 28 3.3 Modeling.................................................. 29 3.3.1 Modeling notes........................................... 31 3.4 Independent variables, scalars and constants............................... 33 3.5 State and control variables......................................... 33 3.6 Boundary, path, event and integral constraints............................. 34 4 Multi-phase optimal control 34 5 Scaling of optimal control problems 34 6 Setting solver and options 35 7 Solving optimal control problems 36 7.1 Standard functions and operators..................................... 36 7.1.1 collocate | Expand a propt tomSym to all collocation points on a phase........... 36 7.1.2 tomSym=dot............................................ 36 7.1.3 final | Evaluate a propt tomSym at the final point of a phase................ 36 7.1.4 icollocate | Expand a propt tomSym to all interpolation points on a phase........ 36 7.1.5 initial | Evaluate a propt tomSym at the initial point of a phase............... 36 7.1.6 integrate | Evaluate the integral of an expression in a phase................. 37 7.1.7 mcollocate | Expand to all collocation points, endpoints and midpoints on a phase.... 37 2 7.1.8 setPhase | Set the active phase when modeling PROPT problem.............. 37 7.1.9 tomControl | Generate a PROPT symbolic state....................... 37 7.1.10 tomControls | Create tomControl objects........................... 38 7.1.11 tomPhase | Create a phase struct............................... 38 7.1.12 tomState | Generate a PROPT symbolic state........................ 38 7.1.13 tomStates | Create tomState objects as toms create tomSym objects............ 39 7.2 Advanced functions and operators.................................... 40 7.2.1 atPoints | Expand a propt tomSym to a set of points on a phase.............. 40 7.2.2 interp1p | Polynomial interpolation............................... 40 7.2.3 proptGausspoints | Generate a list of gauss points....................... 40 7.2.4 proptDiffMatrix | Differentiation matrix for interpPoly.................... 40 7.3 Screen output................................................ 41 7.4 Solution structure............................................. 41 7.5 Plotting................................................... 41 8 jj OPTIMAL CONTROL EXAMPLES jj 42 9 Acrobot 42 9.1 Problem Formulation............................................ 42 10 A Linear Problem with Bang Bang Control 43 10.1 Problem description............................................ 43 10.2 Problem setup............................................... 44 10.3 Solve the problem............................................. 44 10.4 Plot result.................................................. 45 11 Batch Fermentor 47 11.1 Problem description............................................ 47 11.2 Solving the problem on multiple grids................................... 48 11.3 Plot result.................................................. 52 12 Batch Production 58 12.1 Problem description............................................ 58 12.2 Problem setup............................................... 59 12.3 Solve the problem............................................. 61 12.4 Plot result.................................................. 62 13 Batch Reactor Problem 66 3 13.1 Problem description............................................ 66 13.2 Problem setup............................................... 66 13.3 Solve the problem............................................. 67 13.4 Plot result.................................................. 68 14 The Brachistochrone Problem 70 14.1 Problem description............................................ 70 14.2 Problem setup............................................... 70 14.3 Solve the problem............................................. 71 14.4 Plot the result............................................... 72 15 The Brachistochrone Problem (DAE formulation) 73 15.1 DAE formulation.............................................. 73 15.2 Problem setup............................................... 73 15.3 Solve the problem............................................. 74 15.4 Plot the result............................................... 75 16 Bridge Crane System 76 16.1 Problem description............................................ 76 16.2 Problem setup............................................... 77 16.3 Solve the problem............................................. 77 16.4 Plot result.................................................. 78 17 Bryson-Denham Problem 80 17.1 Problem description............................................ 80 17.2 Problem setup............................................... 80 17.3 Solve the problem............................................. 81 17.4 Plot result.................................................. 81 18 Bryson-Denham Problem (Detailed) 83 18.1 Problem description............................................ 83 18.2 Define the independent variable, and phase:............................... 83 18.3 A few constants............................................... 83 18.4 Define a list of states............................................ 83 18.5 Adding the control variable and equations................................ 84 18.6 Equations.................................................. 84 18.7 Build the .m files and general TOMLAB problem............................ 84 4 19 Bryson-Denham Problem (Short version) 86 19.1 Problem description............................................ 86 19.2 Problem setup............................................... 86 20 Bryson-Denham Two Phase Problem 88 20.1 Problem description............................................ 88 20.2 Problem setup............................................... 88 20.3 Solve the problem............................................. 90 20.4 Plot the result............................................... 91 21 Bryson Maxrange 93 21.1 Problem description............................................ 93 21.2 Problem setup............................................... 93 21.3 Solve the problem............................................. 94 21.4 Plot result.................................................. 94 22 Catalyst Mixing 96 22.1 Problem formulation............................................ 96 22.2 Problem setup............................................... 96 22.3 Solve the problem............................................. 97 22.4 Plot result.................................................. 98 23 Catalytic Cracking of Gas Oil 100 23.1 Problem Formulation............................................ 100 23.2 Problem setup............................................... 100 23.3 Solve the problem............................................. 101 23.4 Plot result.................................................. 102 24 Flow in a Channel 103 24.1 Problem Formulation............................................ 103 24.2 Problem setup............................................... 104 24.3 Solve the problem............................................. 104 24.4 Plot result.................................................. 105 25 Coloumb Friction 1 107 25.1 Problem Formulation............................................ 107 25.2 Problem setup............................................... 107 25.3 Solve the problem............................................. 108 5 25.4 Plot result.................................................. 109 26 Coloumb Friction 2 110 26.1 Problem Formulation............................................ 110 26.2 Problem setup............................................... 111 26.3 Solve the problem............................................. 111 26.4 Plot result.................................................. 112 27 Continuous State Constraint Problem 114 27.1 Problem description............................................ 114 27.2 Problem setup............................................... 114 27.3 Solve the problem............................................. 115 27.4 Plot result.................................................. 115 28 Curve Area Maximization 117 28.1 Problem Description............................................ 117 28.2 Problem setup............................................... 117 28.3 Solve the problem............................................. 118 28.4 Plot result.................................................. 118 29 Denbigh's System of Reactions 120 29.1 Problem description............................................ 120 29.2 Problem
Load more

Recommended publications
  • University of California, San Diego
    UNIVERSITY OF CALIFORNIA, SAN DIEGO Computational Methods for Parameter Estimation in Nonlinear Models A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Physics with a Specialization in Computational Physics by Bryan Andrew Toth Committee in charge: Professor Henry D. I. Abarbanel, Chair Professor Philip Gill Professor Julius Kuti Professor Gabriel Silva Professor Frank Wuerthwein 2011 Copyright Bryan Andrew Toth, 2011 All rights reserved. The dissertation of Bryan Andrew Toth is approved, and it is acceptable in quality and form for publication on microfilm and electronically: Chair University of California, San Diego 2011 iii DEDICATION To my grandparents, August and Virginia Toth and Willem and Jane Keur, who helped put me on a lifelong path of learning. iv EPIGRAPH An Expert: One who knows more and more about less and less, until eventually he knows everything about nothing. |Source Unknown v TABLE OF CONTENTS Signature Page . iii Dedication . iv Epigraph . v Table of Contents . vi List of Figures . ix List of Tables . x Acknowledgements . xi Vita and Publications . xii Abstract of the Dissertation . xiii Chapter 1 Introduction . 1 1.1 Dynamical Systems . 1 1.1.1 Linear and Nonlinear Dynamics . 2 1.1.2 Chaos . 4 1.1.3 Synchronization . 6 1.2 Parameter Estimation . 8 1.2.1 Kalman Filters . 8 1.2.2 Variational Methods . 9 1.2.3 Parameter Estimation in Nonlinear Systems . 9 1.3 Dissertation Preview . 10 Chapter 2 Dynamical State and Parameter Estimation . 11 2.1 Introduction . 11 2.2 DSPE Overview . 11 2.3 Formulation . 12 2.3.1 Least Squares Minimization .
    [Show full text]
  • Propt Product Sheet
    PROPT - The world’s fastest Optimal Control platform for MATLAB. PROPT - ONE OF A KIND, LIGHTNING FAST SOLUTIONS TO YOUR OPTIMAL CONTROL PROBLEMS! NOW WITH WELL OVER 100 TEST CASES! The PROPT software package is intended to When using PROPT, optimally coded analytical solve dynamic optimization problems. Such first and second order derivatives, including problems are usually described by: problem sparsity patterns are automatically generated, thereby making it the first MATLAB • A state-space model of package to be able to fully utilize a system. This can be NLP (and QP) solvers such as: either a set of ordinary KNITRO, CONOPT, SNOPT and differential equations CPLEX. (ODE) or differential PROPT currently uses Gauss or algebraic equations (PAE). Chebyshev-point collocation • Initial and/or final for solving optimal control conditions (sometimes problems. However, the code is also conditions at other written in a more general way, points). allowing for a DAE rather than an ODE formulation. Parameter • A cost functional, i.e. a estimation problems are also scalar value that depends possible to solve. on the state trajectories and the control function. PROPT has three main functions: • Sometimes, additional equations and variables • Computation of the that, for example, relate constant matrices used for the the initial and final differentiation and integration conditions to each other. of the polynomials used to approximate the solution to the trajectory optimization problem. The goal of PROPT is to make it possible to input such problem • Source transformation to turn descriptions as simply as user-supplied expressions into possible, without having to worry optimized MATLAB code for the about the mathematics of the cost function f and constraint actual solver.
    [Show full text]
  • Full Text (Pdf)
    A Toolchain for Solving Dynamic Optimization Problems Using Symbolic and Parallel Computing Evgeny Lazutkin Siegbert Hopfgarten Abebe Geletu Pu Li Group Simulation and Optimal Processes, Institute for Automation and Systems Engineering, Technische Universität Ilmenau, P.O. Box 10 05 65, 98684 Ilmenau, Germany. {evgeny.lazutkin,siegbert.hopfgarten,abebe.geletu,pu.li}@tu-ilmenau.de Abstract shown in Fig. 1. Based on the current process state x(k) obtained through the state observer or measurement, Significant progresses in developing approaches to dy- resp., the optimal control problem is solved in the opti- namic optimization have been made. However, its prac- mizer in each sample time. The resulting optimal control tical implementation poses a difficult task and its real- strategy in the first interval u(k) of the moving horizon time application such as in nonlinear model predictive is then realized through the local control system. There- control (NMPC) remains challenging. A toolchain is de- fore, an essential limitation of applying NMPC is due to veloped in this work to relieve the implementation bur- its long computation time taken to solve the NLP prob- den and, meanwhile, to speed up the computations for lem for each sample time, especially for the control of solving the dynamic optimization problem. To achieve fast systems (Wang and Boyd, 2010). In general, the these targets, symbolic computing is utilized for calcu- computation time should be much less than the sample lating the first and second order sensitivities on the one time of the NMPC scheme (Schäfer et al., 2007). Al- hand and parallel computing is used for separately ac- though powerful methods are available, e.g.
    [Show full text]
  • Click to Edit Master Title Style
    Click to edit Master title style MINLP with Combined Interior Point and Active Set Methods Jose L. Mojica Adam D. Lewis John D. Hedengren Brigham Young University INFORM 2013, Minneapolis, MN Presentation Overview NLP Benchmarking Hock-Schittkowski Dynamic optimization Biological models Combining Interior Point and Active Set MINLP Benchmarking MacMINLP MINLP Model Predictive Control Chiller Thermal Energy Storage Unmanned Aerial Systems Future Developments Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University Overview of Benchmark Testing NLP Benchmark Testing 1 1 2 3 3 min J (x, y,u) APOPT , BPOPT , IPOPT , SNOPT , MINOS x Problem characteristics: s.t. 0 f , x, y,u t Hock Schittkowski, Dynamic Opt, SBML 0 g(x, y,u) Nonlinear Programming (NLP) Differential Algebraic Equations (DAEs) 0 h(x, y,u) n m APMonitor Modeling Language x, y u MINLP Benchmark Testing min J (x, y,u, z) 1 1 2 APOPT , BPOPT , BONMIN x s.t. 0 f , x, y,u, z Problem characteristics: t MacMINLP, Industrial Test Set 0 g(x, y,u, z) Mixed Integer Nonlinear Programming (MINLP) 0 h(x, y,u, z) Mixed Integer Differential Algebraic Equations (MIDAEs) x, y n u m z m APMonitor & AMPL Modeling Language 1–APS, LLC 2–EPL, 3–SBS, Inc. Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University NLP Benchmark – Summary (494) 100 90 80 APOPT+BPOPT APOPT 70 1.0 BPOPT 1.0 60 IPOPT 3.10 IPOPT 50 2.3 SNOPT Percentage (%) 6.1 40 Benchmark Results MINOS 494 Problems 5.5 30 20 10 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Not worse than 2 times slower than
    [Show full text]
  • Specifying “Logical” Conditions in AMPL Optimization Models
    Specifying “Logical” Conditions in AMPL Optimization Models Robert Fourer AMPL Optimization www.ampl.com — 773-336-AMPL INFORMS Annual Meeting Phoenix, Arizona — 14-17 October 2012 Session SA15, Software Demonstrations Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 1 New and Forthcoming Developments in the AMPL Modeling Language and System Optimization modelers are often stymied by the complications of converting problem logic into algebraic constraints suitable for solvers. The AMPL modeling language thus allows various logical conditions to be described directly. Additionally a new interface to the ILOG CP solver handles logic in a natural way not requiring conventional transformations. Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 2 AMPL News Free AMPL book chapters AMPL for Courses Extended function library Extended support for “logical” conditions AMPL driver for CPLEX Opt Studio “Concert” C++ interface Support for ILOG CP constraint programming solver Support for “logical” constraints in CPLEX INFORMS Impact Prize to . Originators of AIMMS, AMPL, GAMS, LINDO, MPL Awards presented Sunday 8:30-9:45, Conv Ctr West 101 Doors close 8:45! Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 3 AMPL Book Chapters now free for download www.ampl.com/BOOK/download.html Bound copies remain available purchase from usual
    [Show full text]
  • Optimal Control Theory Version 0.2
    An Introduction to Mathematical Optimal Control Theory Version 0.2 By Lawrence C. Evans Department of Mathematics University of California, Berkeley Chapter 1: Introduction Chapter 2: Controllability, bang-bang principle Chapter 3: Linear time-optimal control Chapter 4: The Pontryagin Maximum Principle Chapter 5: Dynamic programming Chapter 6: Game theory Chapter 7: Introduction to stochastic control theory Appendix: Proofs of the Pontryagin Maximum Principle Exercises References 1 PREFACE These notes build upon a course I taught at the University of Maryland during the fall of 1983. My great thanks go to Martino Bardi, who took careful notes, saved them all these years and recently mailed them to me. Faye Yeager typed up his notes into a first draft of these lectures as they now appear. Scott Armstrong read over the notes and suggested many improvements: thanks, Scott. Stephen Moye of the American Math Society helped me a lot with AMSTeX versus LaTeX issues. My thanks also to Atilla Yilmaz for spotting lots of typos and errors, which I have corrected. I have radically modified much of the notation (to be consistent with my other writings), updated the references, added several new examples, and provided a proof of the Pontryagin Maximum Principle. As this is a course for undergraduates, I have dispensed in certain proofs with various measurability and continuity issues, and as compensation have added various critiques as to the lack of total rigor. This current version of the notes is not yet complete, but meets I think the usual high standards for material posted on the internet. Please email me at [email protected] with any corrections or comments.
    [Show full text]
  • An Algorithm for Bang–Bang Control of Fixed-Head Hydroplants
    International Journal of Computer Mathematics Vol. 88, No. 9, June 2011, 1949–1959 An algorithm for bang–bang control of fixed-head hydroplants L. Bayón*, J.M. Grau, M.M. Ruiz and P.M. Suárez Department of Mathematics, University of Oviedo, Oviedo, Spain (Received 31 August 2009; revised version received 10 March 2010; second revision received 1 June 2010; accepted 12 June 2010) This paper deals with the optimal control (OC) problem that arise when a hydraulic system with fixed-head hydroplants is considered. In the frame of a deregulated electricity market, the resulting Hamiltonian for such OC problems is linear in the control variable and results in an optimal singular/bang–bang control policy. To avoid difficulties associated with the computation of optimal singular/bang–bang controls, an efficient and simple optimization algorithm is proposed. The computational technique is illustrated on one example. Keywords: optimal control; singular/bang–bang problems; hydroplants 2000 AMS Subject Classification: 49J30 1. Introduction The computation of optimal singular/bang–bang controls is of particular interest to researchers because of the difficulty in obtaining the optimal solution. Several engineering control problems, Downloaded By: [Bayón, L.] At: 08:38 25 May 2011 such as the chemical reactor start-up or hydrothermal optimization problems, are known to have optimal singular/bang–bang controls. This paper deals with the optimal control (OC) problem that arises when addressing the new short-term problems that are faced by a generation company in a deregulated electricity market. Our model of the spot market explicitly represents the price of electricity as a known exogenous variable and we consider a system with fixed-head hydroplants.
    [Show full text]
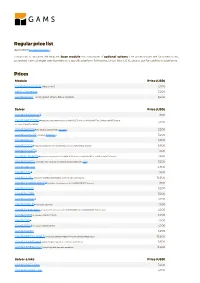
  • Standard Price List
    Regular price list April 2021 (Download PDF ) This price list includes the required base module and a number of optional solvers. The prices shown are for unrestricted, perpetual named single user licenses on a specific platform (Windows, Linux, Mac OS X), please ask for additional platforms. Prices Module Price (USD) GAMS/Base Module (required) 3,200 MIRO Connector 3,200 GAMS/Secure - encrypted Work Files Option 3,200 Solver Price (USD) GAMS/ALPHAECP 1 1,600 GAMS/ANTIGONE 1 (requires the presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license, 3,200 includes GAMS/GLOMIQO) GAMS/BARON 1 (for details please follow this link ) 3,200 GAMS/CONOPT (includes CONOPT 4 ) 3,200 GAMS/CPLEX 9,600 GAMS/DECIS 1 (requires presence of a GAMS/CPLEX or a GAMS/MINOS license) 9,600 GAMS/DICOPT 1 1,600 GAMS/GLOMIQO 1 (requires presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license) 1,600 GAMS/IPOPTH (includes HSL-routines, for details please follow this link ) 3,200 GAMS/KNITRO 4,800 GAMS/LGO 2 1,600 GAMS/LINDO (includes GAMS/LINDOGLOBAL with no size restrictions) 12,800 GAMS/LINDOGLOBAL 2 (requires the presence of a GAMS/CONOPT license) 1,600 GAMS/MINOS 3,200 GAMS/MOSEK 3,200 GAMS/MPSGE 1 3,200 GAMS/MSNLP 1 (includes LSGRG2) 1,600 GAMS/ODHeuristic (requires the presence of a GAMS/CPLEX or a GAMS/CPLEX-link license) 3,200 GAMS/PATH (includes GAMS/PATHNLP) 3,200 GAMS/SBB 1 1,600 GAMS/SCIP 1 (includes GAMS/SOPLEX) 3,200 GAMS/SNOPT 3,200 GAMS/XPRESS-MINLP (includes GAMS/XPRESS-MIP and GAMS/XPRESS-NLP) 12,800 GAMS/XPRESS-MIP (everything but general nonlinear equations) 9,600 GAMS/XPRESS-NLP (everything but discrete variables) 6,400 Solver-Links Price (USD) GAMS/CPLEX Link 3,200 GAMS/GUROBI Link 3,200 Solver-Links Price (USD) GAMS/MOSEK Link 1,600 GAMS/XPRESS Link 3,200 General information The GAMS Base Module includes the GAMS Language Compiler, GAMS-APIs, and many utilities .
    [Show full text]
  • Optimal Steering Control Input Generation for Vehicle's Entry Speed Maximization in a Double-Lane Change Manoeuvre
    Optimal steering control input generation for vehicle's entry speed maximization in a double-lane change manoeuvre Matthias Tidlund Stavros Angelis Vehicle Engineering KTH Royal Institute of Technology Master Thesis TRITA-AVE 2013:64 ISSN 1651-7660 Postal address Visiting Address Telephone Telefax Internet KTH Teknikringen 8 +46 8 790 6000 +46 8 790 9290 www.kth.se Vehicle Dynamics Stockholm SE-100 44 Stockholm, Sweden Acknowledgment This thesis study was performed between June and November 2013 at Volvo Cars’ Active Safety CAE department, which provided a really inspiring environment with skilled colleagues and the opportunity to get an insight of their work. Our Volvo Cars supervisor Diomidis Katzourakis, CAE Vehicle Dynamics engineer, has constantly provided invaluable feedback regarding both the content of the thesis as well as our presentations at Volvo. He has been a great knowledge asset and always available as source of answers and ideas when the vehicle’s dynamic complexity was decided and modelled. We also would like to thank our supervisor Mikael Nybacka, Assistant Professor in Vehicle Dynamics at KTH Royal Institute of Technology, for the support and guidance to reach the goal of delivering a report of high quality, for the scheduling and the timeline of this work, and the opportunity to present this work in parts so to have a better overview of its progress and quality. A special thanks should also be given to Mathias Lidberg, Associate Professor in Vehicle Dynamics at Chalmers Technical University, for his active participation in the project, not only saving us a great deal of time in the beginning by helping us understand the optimization tool Tomlab and the parts within an optimization problem which are most important, but also for constantly providing input with ideas and feedback.
    [Show full text]
  • Basic Implementation of Multiple-Interval Pseudospectral Methods to Solve Optimal Control Problems
    Basic Implementation of Multiple-Interval Pseudospectral Methods to Solve Optimal Control Problems Technical Report UIUC-ESDL-2015-01 Daniel R. Herber∗ Engineering System Design Lab University of Illinois at Urbana-Champaign June 4, 2015 Abstract A short discussion of optimal control methods is presented including in- direct, direct shooting, and direct transcription methods. Next the basics of multiple-interval pseudospectral methods are given independent of the nu- merical scheme to highlight the fundamentals. The two numerical schemes discussed are the Legendre pseudospectral method with LGL nodes and the Chebyshev pseudospectral method with CGL nodes. A brief comparison be- tween time-marching direct transcription methods and pseudospectral direct transcription is presented. The canonical Bryson-Denham state-constrained double integrator optimal control problem is used as a test optimal control problem. The results from the case study demonstrate the effect of user's choice in mesh parameters and little difference between the two numerical pseudospectral schemes. ∗Ph.D pre-candidate in Systems and Entrepreneurial Engineering, Department of In- dustrial and Enterprise Systems Engineering, University of Illinois at Urbana-Champaign, [email protected] c 2015 Daniel R. Herber 1 Contents 1 Optimal Control and Direct Transcription 3 2 Basics of Pseudospectral Methods 4 2.1 Foundation . 4 2.2 Multiple Intervals . 7 2.3 Legendre Pseudospectral Method with LGL Nodes . 9 2.4 Chebyshev Pseudospectral Method with CGL Nodes . 10 2.5 Brief Comparison to Time-Marching Direct Transcription Methods 11 3 Numeric Case Study 14 3.1 Test Problem Description . 14 3.2 Implementation and Analysis Details . 14 3.3 Summary of Case Study Results .
    [Show full text]
  • Nature-Inspired Metaheuristic Algorithms for Finding Efficient
    Nature-Inspired Metaheuristic Algorithms for Finding Efficient Experimental Designs Weng Kee Wong Department of Biostatistics Fielding School of Public Health October 19, 2012 DAE 2012 Department of Statistics University of Georgia October 17-20th 2012 Weng Kee Wong (Department of Biostatistics [email protected] School of Public Health ) October19,2012 1/50 Two Upcoming Statistics Conferences at UCLA Western Northern American Region (WNAR 2013) June 16-19 2013 http://www.wnar.org Weng Kee Wong (Dept. of Biostatistics [email protected] of Public Health ) October19,2012 2/50 Two Upcoming Statistics Conferences at UCLA Western Northern American Region (WNAR 2013) June 16-19 2013 http://www.wnar.org The 2013 Spring Research Conference (SRC) on Statistics in Industry and Technology June 20-22 2013 http://www.stat.ucla.edu/ hqxu/src2013 Weng Kee Wong (Dept. of Biostatistics [email protected] of Public Health ) October19,2012 2/50 Two Upcoming Statistics Conferences at UCLA Western Northern American Region (WNAR 2013) June 16-19 2013 http://www.wnar.org The 2013 Spring Research Conference (SRC) on Statistics in Industry and Technology June 20-22 2013 http://www.stat.ucla.edu/ hqxu/src2013 Beverly Hills, Brentwood, Bel Air, Westwood, Wilshire Corridor Weng Kee Wong (Dept. of Biostatistics [email protected] of Public Health ) October19,2012 2/50 Two Upcoming Statistics Conferences at UCLA Western Northern American Region (WNAR 2013) June 16-19 2013 http://www.wnar.org The 2013 Spring Research Conference (SRC) on Statistics in Industry and Technology June 20-22 2013 http://www.stat.ucla.edu/ hqxu/src2013 Beverly Hills, Brentwood, Bel Air, Westwood, Wilshire Corridor Close to the Pacific Ocean Weng Kee Wong (Dept.
    [Show full text]
  • OPTIMAL CONTROL of NONHOLONOMIC MECHANICAL SYSTEMS By
    OPTIMAL CONTROL OF NONHOLONOMIC MECHANICAL SYSTEMS by Stuart Marcus Rogers A thesis submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Applied Mathematics Department of Mathematical and Statistical Sciences University of Alberta ⃝c Stuart Marcus Rogers, 2017 Abstract This thesis investigates the optimal control of two nonholonomic mechanical systems, Suslov's problem and the rolling ball. Suslov's problem is a nonholonomic variation of the classical rotating free rigid body problem, in which the body angular velocity Ω(t) must always be orthogonal to a prescribed, time-varying body frame vector ξ(t), i.e. hΩ(t); ξ(t)i = 0. The motion of the rigid body in Suslov's problem is actuated via ξ(t), while the motion of the rolling ball is actuated via internal point masses that move along rails fixed within the ball. First, by applying Lagrange-d'Alembert's principle with Euler-Poincar´e'smethod, the uncontrolled equations of motion are derived. Then, by applying Pontryagin's minimum principle, the controlled equations of motion are derived, a solution of which obeys the uncontrolled equations of motion, satisfies prescribed initial and final conditions, and minimizes a prescribed performance index. Finally, the controlled equations of motion are solved numerically by a continuation method, starting from an initial solution obtained analytically (in the case of Suslov's problem) or via a direct method (in the case of the rolling ball). ii Preface This thesis contains material that has appeared in a pair of papers, one on Suslov's problem and the other on rolling ball robots, co-authored with my supervisor, Vakhtang Putkaradze.
    [Show full text]