DOCSLIB.ORG

The Kronecker Product a Product of the Times

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Kronecker Product a Product of the Times The Kronecker Product A Product of the Times Charles Van Loan Department of Computer Science Cornell University Presented at the SIAM Conference on Applied Linear Algebra, Monterey, Califirnia, October 26, 2009 The Kronecker Product B C is a block matrix whose ij-th block is b C. ⊗ ij E.g., b b b11C b12C 11 12 C = b b ⊗ 21 22 b21C b22C Also called the “Direct Product” or the “Tensor Product” Every bijckl Shows Up c11 c12 c13 b11 b12 c21 c22 c23 b21 b22 ⊗ c31 c32 c33 = b11c11 b11c12 b11c13 b12c11 b12c12 b12c13 b11c21 b11c22 b11c23 b12c21 b12c22 b12c23 b c b c b c b c b c b c 11 31 11 32 11 33 12 31 12 32 12 33 b c b c b c b c b c b c 21 11 21 12 21 13 22 11 22 12 22 13 b21c21 b21c22 b21c23 b22c21 b22c22 b22c23 b21c31 b21c32 b21c33 b22c31 b22c32 b22c33 Basic Algebraic Properties (B C)T = BT CT ⊗ ⊗ (B C) 1 = B 1 C 1 ⊗ − − ⊗ − (B C)(D F ) = BD CF ⊗ ⊗ ⊗ B (C D) =(B C) D ⊗ ⊗ ⊗ ⊗ C B = (Perfect Shuffle)T (B C)(Perfect Shuffle) ⊗ ⊗ R.J. Horn and C.R. Johnson(1991). Topics in Matrix Analysis, Cambridge University Press, NY. Reshaping KP Computations 2 Suppose B, C IRn n and x IRn . ∈ × ∈ The operation y =(B C)x is O(n4): ⊗ y = kron(B,C)*x The equivalent, reshaped operation Y = CXBT is O(n3): y = reshape(C*reshape(x,n,n)*B’,n,n) H.V. Henderson and S.R.Searle (1981). “The Vec-Permutation Matrix, The Vec Operator, and Kronecker Products, A Review,” Linear and Mulitilinear Algebra, 9, 271–288. Talk Outline 1. The 1800’s Origins: Z 2. The 1900’s Heightened Profile: ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ 3. The 2000’s Future: ∞ The 1800’s Z Products and Deltas δ ⊗ ij Leopold Kronecker (1823–1891) Of course, the contributions go far beyond this... E.T. Bell (1937). Men of Mathematics, Simon and Schuster, New York. K. Hensel (1968). Leopold Kronecker’s Werke, Chelsea Publishing Company, New York. Brief Survey of the Kronecker Delta T U δijV = δij 1 κ2(δ ) = ij δij G.H. Golub and C. Van Loan (1996). Matrix Computations, 3rd Ed., Johns Hopkins University Press, Baltimore, Maryland. Acknowledgement H.V. Henderson, F. Pukelsheim, and S.R. Searle (1983). “On the History of the Kronecker Product,” Linear and Multilinear Algebra 14, 113–120. Shayle Searle, Professor Emeritus, Cornell University (right) Scandal! H.V. Henderson, F. Pukelsheim, and S.R. Searle (1983). “On the History of the Kronecker Product,” Linear and Multilinear Algebra 14, 113–120. Abstract History reveals that what is today called the Kro- necker product should be called the Zehfuss Product. This fact is somewhat appreciated by the modern (numerical) linear algebra community: R.J. Horn and C.R. Johnson(1991). Topics in Matrix Analysis, Cambridge University Press, NY, p. 254. A.N. Langville and W.J. Stewart (2004). “The Kronecker product and stochastic automata networks,” J. Computational and Applied Mathematics 167, 429–447. Who Was Zehfuss? Born 1832. Obscure professor of mathematics at University of Heidelberg for a while. Then went on to other things. Wrote papers on determinants... G. Zehfuss (1858). “Uber¨ eine gewisse Determinante,” Zeitschrift f¨ur Mathematik und Physik 3, 298–301. Main Result a.k.a. “The Z Theorem” If B IRm m and C IRn n then ∈ × ∈ × det(B C) = det(B)ndet(C)m ⊗ Modern Proof Note that In B and Im C are block diagonal and take determinants in ⊗ ⊗ T B C = (B In)(Im C) = P (In B)P (Im C) ⊗ ⊗ ⊗ ⊗ ⊗ where P is a perfect shuffle permutation. Excerpts from Zehfuss(1858) a a b b c c d d 1A1 1B1 1A1 1B1 1A1 1B1 1A1 1B1 a1 2 a1 2 b1 2 b1 2 c1 2 c1 2 d1 2 d1 2 A B A B A B A B a2 1 a2 1 b2 1 b2 1 c2 1 c2 1 d2 1 d2 1 A B A B A B A B a2 2 a2 2 b2 2 b2 2 c2 2 c2 2 d2 2 d2 2 A B A B A B A B ∆ = a a b b c c d d 3 1 3 1 3 1 3 1 3 1 3 1 3 1 3 1 A B A B A B A B a3 2 a3 2 b3 2 b3 2 c3 2 c3 2 d3 2 d3 2 A B A B A B A B a4 1 a4 1 b4 1 b4 1 c4 1 c4 1 d4 1 d4 1 A B A B A B A B a a b b c c d d 4A2 4B2 4A2 4B2 4A2 4B2 4A2 4B2 Excerpts from Zehfuss(1858) a1 b1 c1 d1 a2 b2 c2 d2 1 1 p = und P = A B a3 b3 c3 d3 2 2 A B a b c d 4 4 4 4 2 4 ∆2 2,2 = p4P2 M m ∆2 Mm = p P Hensel (1891) Student in Berlin 1880-1884. Maintains that Kronecker presented the Z-theorem in his lectures. K. Hensel (1891). “Uber¨ die Darstellung der Determinante eines Systems, welches aus zwei anderen componirt ist,” ACTA Mathematica 14, 317–319. The 1900’s ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ ⊗ Muir (1911) Attributes the Z-theorem to Zehfuss. Calls det(B C) the “Zehfuss determinant.” ⊗ T. Muir (1911). The Theory of Determinants in the Historical Order of Development, Vols 1-4, Dover, NY. Rutherford(1933) Q. When are two Zehfuss matrices equal? ??? B C F G ⊗ = ⊗ Subscripting from zero, if B (m n ), C (mc nc), F (m n ), b× b × f × f G (mg ng), then (B C) = (F G) means × ⊗ ij ⊗ ij B(floor(i/mc), floor(j/nc)) C(i mod mc,j mod nc) · = F (floor(i/mg), floor(j/ng)) G(i mod mg,j mod ng) · D.E. Rutherford (1933). “On the Condition that Two Zehfuss Matrices are Equal,” Bull. Amer. Math. Soc. 39, 801-808. Z Why? → ⊗ “...a series of influential texts at and after the turn of the century permanently associated Kronecker’s name with the “ ” product and this terminology is nearly universal to- ⊗ day.” Horn and Johnson (1991) “...the textbook of Scott and Matthews (1904) which ap- peared four years after the publication of Rados’ paper, gave new life to the old error. This was probably due to the teaching of Pascal, whose second edition (1923) still propagates the error [of the first edition (1897).]” Muir (1927) Heightened Profile Beginning in the 60s Some Reasons Regular Grids Tensoring Low Dimension Ideas Higher Order Statistics Fast Transforms Preconditioners Quantum Computing Tensor Decompositions/Approximations C. Van Loan (2000). “The Ubiquitous Kronecker Product,” Journal of Computational and Applied Math- ematics,, 85-100. Regular Grids (M +1)-by-(N +1) discretization of the Laplacian on a rectangle... A = I T + T I M ⊗ N M ⊗ N 2 1 0 0 0 1− 2 1 0 0 − − T = 0 1 2 1 0 5 − − 0 0 1 2 1 − − 0 0 0 1 2 − F.W. Dorr (1970). “The Direct Solution of the Discrete Poisson Equation on a Rectangle,” SIAM Review 12, 248–263. G.H. Golub and C.F. Van Loan (1996). Matrix Computations, 3rd Ed, Johns Hopkins University Press, Baltimore, MD. Tensoring Low Dimension Ideas b n T f(x) dx wi f(xi) = w f(x) a ≈ Z Xi=1 b b b nx ny nz 1 2 3 (x) (y) (z) f(x,y,z) dxdydz wi wj wk f(xi, yj,zk) a1 a2 a3 ≈ Z Z Z Xi=1 Xj=1 Xk=1 =(w(x) w(y) w(z))T f(x y z) ⊗ ⊗ ⊗ ⊗ A. Graham (1981). Kronecker Products and Matrix Calculus with Applications, Ellis Horwood Ltd, Chich- ester, England. Higher Order Statistics E(xxT ) E(x⇓ x) ⊗ E(x x ⇓ x) ⊗ ⊗ ··· ⊗ Kronecker powers: kA = A A A (k times) ⊗ ⊗ ⊗ ··· ⊗ T.F. Andre, R.D. Nowak, and B.D. Van Veen (1997). “Low Rank Estimation of Higher Order Statistics,” IEEE Trans. Signal Processing 45, 673–685. Fast Transforms FFT F P = B (I B )(I B )(I B ) 16 16 16 2 ⊗ 8 4 ⊗ 4 8 ⊗ 2 10 1 0 0 1 0 ω4 B = ωn = exp( 2πi/n) 4 1 0 1 0 − − 0 1 0 ω − 4 J. Granata, M. Conner, and R. Tolimieri (1992). “Recursive Fast Algorithms and the Role of the Tensor Product,” IEEE Transactions on Signal Processing 40, 2921–2930. C. Van Loan(1992). Computational Frameworks for the Fast Fourier Transform, SIAM Publications, Philadelphia, PA. Fast Transforms Cont’d Haar Wavelet Transform 1 1 W I if m> 1 m ⊗ 1 m ⊗ 1 W2m = − . [1] if m = 1 Fast Gauss Transform 2 g = exp( s t /δ) G = Gnear + G ij −k j − i k2 ⇒ far Gnear involves a Kronecker Product G. Strang(1993). “Wavelet Transforms Versus Fourier Transforms,” Bulletin of the American Mathematical Association, 28, 288–305. X. Sun and Y. Bao (2003). “A Kronecker Product Represenation of the Fast Gauss Transform,” SIAM J. Matrix Anal. Appl., 24, 768–786. Preconditioners If A B C, then B C has potential as a preconditioner. ≈ ⊗ ⊗ It captures the essence of A. It is easy to solve (B C)z = r. ⊗ Good Example: A band block Toeplitz with banded Toeplitz blocks. B and C chosen to be band Toeplitz. J. Kamm and J.G. Nagy (2000). “Optimal Kronecker Product Approximation of Block Toeplitz Matrices,” SIAM J. Matrix Anal. and Appl., 22, 155–172. J. Nagy and M. Kilmer (2006).
Load more

Recommended publications
  • Block Kronecker Products and the Vecb Operator* CORE View
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Block Kronecker Products and the vecb Operator* Ruud H. Koning Department of Economics University of Groningen P.O. Box 800 9700 AV, Groningen, The Netherlands Heinz Neudecker+ Department of Actuarial Sciences and Econometrics University of Amsterdam Jodenbreestraat 23 1011 NH, Amsterdam, The Netherlands and Tom Wansbeek Department of Economics University of Groningen P.O. Box 800 9700 AV, Groningen, The Netherlands Submitted hv Richard Rrualdi ABSTRACT This paper is concerned with two generalizations of the Kronecker product and two related generalizations of the vet operator. It is demonstrated that they pairwise match two different kinds of matrix partition, viz. the balanced and unbalanced ones. Relevant properties are supplied and proved. A related concept, the so-called tilde transform of a balanced block matrix, is also studied. The results are illustrated with various statistical applications of the five concepts studied. *Comments of an anonymous referee are gratefully acknowledged. ‘This work was started while the second author was at the Indian Statistiral Institute, New Delhi. LINEAR ALGEBRA AND ITS APPLICATIONS 149:165-184 (1991) 165 0 Elsevier Science Publishing Co., Inc., 1991 655 Avenue of the Americas, New York, NY 10010 0024-3795/91/$3.50 166 R. H. KONING, H. NEUDECKER, AND T. WANSBEEK INTRODUCTION Almost twenty years ago Singh [7] and Tracy and Singh [9] introduced a generalization of the Kronecker product A@B. They used varying notation for this new product, viz. A @ B and A &3B. Recently, Hyland and Collins [l] studied the-same product under rather restrictive order conditions.
    [Show full text]
  • The Partition Algebra and the Kronecker Product (Extended Abstract)
    FPSAC 2013, Paris, France DMTCS proc. (subm.), by the authors, 1–12 The partition algebra and the Kronecker product (Extended abstract) C. Bowman1yand M. De Visscher2 and R. Orellana3z 1Institut de Mathematiques´ de Jussieu, 175 rue du chevaleret, 75013, Paris 2Centre for Mathematical Science, City University London, Northampton Square, London, EC1V 0HB, England. 3 Department of Mathematics, Dartmouth College, 6188 Kemeny Hall, Hanover, NH 03755, USA Abstract. We propose a new approach to study the Kronecker coefficients by using the Schur–Weyl duality between the symmetric group and the partition algebra. Resum´ e.´ Nous proposons une nouvelle approche pour l’etude´ des coefficients´ de Kronecker via la dualite´ entre le groupe symetrique´ et l’algebre` des partitions. Keywords: Kronecker coefficients, tensor product, partition algebra, representations of the symmetric group 1 Introduction A fundamental problem in the representation theory of the symmetric group is to describe the coeffi- cients in the decomposition of the tensor product of two Specht modules. These coefficients are known in the literature as the Kronecker coefficients. Finding a formula or combinatorial interpretation for these coefficients has been described by Richard Stanley as ‘one of the main problems in the combinatorial rep- resentation theory of the symmetric group’. This question has received the attention of Littlewood [Lit58], James [JK81, Chapter 2.9], Lascoux [Las80], Thibon [Thi91], Garsia and Remmel [GR85], Kleshchev and Bessenrodt [BK99] amongst others and yet a combinatorial solution has remained beyond reach for over a hundred years. Murnaghan discovered an amazing limiting phenomenon satisfied by the Kronecker coefficients; as we increase the length of the first row of the indexing partitions the sequence of Kronecker coefficients obtained stabilises.
    [Show full text]
  • Kronecker Products
    Copyright ©2005 by the Society for Industrial and Applied Mathematics This electronic version is for personal use and may not be duplicated or distributed. Chapter 13 Kronecker Products 13.1 Definition and Examples Definition 13.1. Let A ∈ Rm×n, B ∈ Rp×q . Then the Kronecker product (or tensor product) of A and B is defined as the matrix a11B ··· a1nB ⊗ = . ∈ Rmp×nq A B . .. . (13.1) am1B ··· amnB Obviously, the same definition holds if A and B are complex-valued matrices. We restrict our attention in this chapter primarily to real-valued matrices, pointing out the extension to the complex case only where it is not obvious. Example 13.2. = 123 = 21 1. Let A 321and B 23. Then 214263 B 2B 3B 234669 A ⊗ B = = . 3B 2BB 634221 694623 Note that B ⊗ A = A ⊗ B. ∈ Rp×q ⊗ = B 0 2. For any B , I2 B 0 B . Replacing I2 by In yields a block diagonal matrix with n copies of B along the diagonal. 3. Let B be an arbitrary 2 × 2 matrix. Then b11 0 b12 0 0 b11 0 b12 B ⊗ I2 = . b21 0 b22 0 0 b21 0 b22 139 “ajlbook” — 2004/11/9 — 13:36 — page 139 — #147 From "Matrix Analysis for Scientists and Engineers" Alan J. Laub. Buy this book from SIAM at www.ec-securehost.com/SIAM/ot91.html Copyright ©2005 by the Society for Industrial and Applied Mathematics This electronic version is for personal use and may not be duplicated or distributed. 140 Chapter 13. Kronecker Products The extension to arbitrary B and In is obvious.
    [Show full text]
  • A Constructive Arbitrary-Degree Kronecker Product Decomposition of Tensors
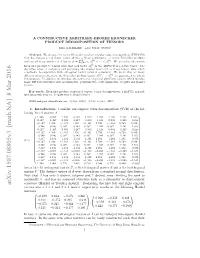
    A CONSTRUCTIVE ARBITRARY-DEGREE KRONECKER PRODUCT DECOMPOSITION OF TENSORS KIM BATSELIER AND NGAI WONG∗ Abstract. We propose the tensor Kronecker product singular value decomposition (TKPSVD) that decomposes a real k-way tensor A into a linear combination of tensor Kronecker products PR (d) (1) with an arbitrary number of d factors A = j=1 σj Aj ⊗ · · · ⊗ Aj . We generalize the matrix (i) Kronecker product to tensors such that each factor Aj in the TKPSVD is a k-way tensor. The algorithm relies on reshaping and permuting the original tensor into a d-way tensor, after which a polyadic decomposition with orthogonal rank-1 terms is computed. We prove that for many (1) (d) different structured tensors, the Kronecker product factors Aj ;:::; Aj are guaranteed to inherit this structure. In addition, we introduce the new notion of general symmetric tensors, which includes many different structures such as symmetric, persymmetric, centrosymmetric, Toeplitz and Hankel tensors. Key words. Kronecker product, structured tensors, tensor decomposition, TTr1SVD, general- ized symmetric tensors, Toeplitz tensor, Hankel tensor AMS subject classifications. 15A69, 15B05, 15A18, 15A23, 15B57 1. Introduction. Consider the singular value decomposition (SVD) of the fol- lowing 16 × 9 matrix A~ 0 1:108 −0:267 −1:192 −0:267 −1:192 −1:281 −1:192 −1:281 1:102 1 B 0:417 −1:487 −0:004 −1:487 −0:004 −1:418 −0:004 −1:418 −0:228C B C B−0:127 1:100 −1:461 1:100 −1:461 0:729 −1:461 0:729 0:940 C B C B−0:748 −0:243 0:387 −0:243 0:387 −1:241 0:387 −1:241 −1:853C B C B 0:417
    [Show full text]
  • Introduction to Kronecker Products
    Math 515 Fall, 2010 Introduction to Kronecker Products If A is an m × n matrix and B is a p × q matrix, then the Kronecker product of A and B is the mp × nq matrix 2 3 a11B a12B ··· a1nB 6 7 6 a21B a22B ··· a2nB 7 A ⊗ B = 6 . 7 6 . 7 4 . 5 am1B am2B ··· amnB Note that if A and B are large matrices, then the Kronecker product A⊗B will be huge. MATLAB has a built-in function kron that can be used as K = kron(A, B); However, you will quickly run out of memory if you try this for matrices that are 50 × 50 or larger. Fortunately we can exploit the block structure of Kronecker products to do many compu- tations involving A ⊗ B without actually forming the Kronecker product. Instead we need only do computations with A and B individually. To begin, we state some very simple properties of Kronecker products, which should not be difficult to verify: • (A ⊗ B)T = AT ⊗ BT • If A and B are square and nonsingular, then (A ⊗ B)−1 = A−1 ⊗ B−1 • (A ⊗ B)(C ⊗ D) = AC ⊗ BD The next property we want to consider involves the matrix-vector multiplication y = (A ⊗ B)x; where A 2 Rm×n and B 2 Rp×q. Thus A ⊗ B 2 Rmp×nq, x 2 Rnq, and y 2 Rmp. Our goal is to exploit the block structure of the Kronecker product matrix to compute y without explicitly forming (A ⊗ B). To see how this can be done, first partition the vectors x and y as 2 3 2 3 x1 y1 6 x 7 6 y 7 6 2 7 q 6 2 7 p x = 6 .
    [Show full text]
  • Kronecker Products and Matrix Calculus in System Theory
    772 IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS, VOL. CAS-25, NO. 9, ISEFTEMBER 1978 Kronecker Products and Matrix Calculus in System Theory JOHN W. BREWER I Absfrucr-The paper begins with a review of the algebras related to and are based on the developments of Section IV. Also, a Kronecker products. These algebras have several applications in system novel and interesting operator notation will ble introduced theory inclluding the analysis of stochastic steady state. The calculus of matrk valued functions of matrices is reviewed in the second part of the in Section VI. paper. This cakuhs is then used to develop an interesting new method for Concluding comments are placed in Section VII. the identification of parameters of linear time-invariant system models. II. NOTATION I. INTRODUCTION Matrices will be denoted by upper case boldface (e.g., HE ART of differentiation has many practical ap- A) and column matrices (vectors) will be denoted by T plications in system analysis. Differentiation is used lower case boldface (e.g., x). The kth row of a matrix such. to obtain necessaryand sufficient conditions for optimiza- as A will be denoted A,. and the kth colmnn will be tion in a.nalytical studies or it is used to obtain gradients denoted A.,. The ik element of A will be denoted ujk. and Hessians in numerical optimization studies. Sensitiv- The n x n unit matrix is denoted I,,. The q-dimensional ity analysis is yet another application area for. differentia- vector which is “I” in the kth and zero elsewhereis called tion formulas. In turn, sensitivity analysis is applied to the the unit vector and is denoted design of feedback and adaptive feedback control sys- tems.
    [Show full text]
  • Representing Words in a Geometric Algebra
    Representing Words in a Geometric Algebra Arjun Mani Princeton University [email protected] Abstract Word embeddings, or the mapping of words to vectors, demonstrate interesting properties such as the ability to solve analogies. However, these models fail to capture many key properties of words (e.g. hierarchy), and one might ask whether there are objects that can better capture the complexity associated with words. Geometric algebra is a branch of mathematics that is characterized by algebraic operations on objects having geometric meaning. In this system objects are linear combinations of subspaces rather than vectors, and certain operations have the significance of intersecting or unioning these subspaces. In this paper we introduce and motivate geometric algebra as a better representation for word embeddings. Next we describe how to implement the geometric product and interestingly show that neural networks can learn this product. We then introduce a model that represents words as objects in this algebra and benchmark it on large corpuses; our results show some promise on traditional word embedding tasks. Thus, we lay the groundwork for further investigation of geometric algebra in word embeddings. 1 Motivation Words are complex creatures; a single word has one (or multiple) semantic meanings, plays a particular syntactic role in a sentence, and has complex relationships with different words (simple examples of such relationships are synonyms and antonyms). The representations of words as vectors, and the ability of these models to capture some of this complexity, has been a seminal advance in the field of natural language processing. Such word embedding models (first introduced by Mikolov et al.
    [Show full text]
  • Spectral Properties of Sums of Certain Kronecker Products
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Linear Algebra and its Applications 431 (2009) 1691–1701 Contents lists available at ScienceDirect Linear Algebra and its Applications journal homepage: www.elsevier.com/locate/laa Spectral properties of sums of certain Kronecker products ∗ Jun-e Feng a, James Lam b, , Yimin Wei c a School of Mathematics, Shandong University, Jinan 250100, People’s Republic of China b Department of Mechanical Engineering, University of Hong Kong, Pokfulam Road, Hong Kong c School of Mathematics, Fudan University, Shanghai 20043, People’s Republic of China ARTICLE INFO ABSTRACT Article history: We introduce two kinds of sums of Kronecker products, and their Received 22 September 2008 induced operators. We study the algebraic properties of these two Accepted 4 June 2009 kinds of matrices and their associated operators; the properties Available online 4 July 2009 include their eigenvalues, their eigenvectors, and the relationships Submitted by C.K. Li between their spectral radii or spectral abscissae. Furthermore, two projected matrices of these Kronecker products and their induced Keywords: operators are also studied. Eigenvalue © 2009 Elsevier Inc. All rights reserved. Eigenvector Spectrum Kronecker product Spectral abscissa Spectral radius 1. Introduction Kronecker product, also called direct product or tensor product, is an operation which owes its origin from group theory and has important applications in physics [6]. Techniques involving Kronecker products have been successfully applied in many fields of matrix theory because of its computational and notational advantages, see [1,2,5,7,8,12,13] and references therein.
    [Show full text]
  • Determinants in the Kronecker Product of Matrices: the Incidence Matrix of a Complete Graph
    DETERMINANTS IN THE KRONECKER PRODUCT OF MATRICES: THE INCIDENCE MATRIX OF A COMPLETE GRAPH CHRISTOPHER R.H. HANUSA AND THOMAS ZASLAVSKY Abstract. We investigate the least common multiple of all sub- determinants, lcmd(A⊗ B), of a Kronecker product of matrices, of which one is an integral matrix A with two columns and the other is the incidence matrix of a complete graph with n vertices. We prove that this quantity is the least common multiple of lcmd(A) to the power n − 1 and certain binomial functions of the entries of A. 1. Introduction In a study of non-attacking placements of chess pieces, Chaiken, Hanusa, and Zaslavsky [1] were led to a quasipolynomial formula that depends in part on the least common multiple of the determinants of all square submatrices of a certain Kronecker product matrix, namely, the Kronecker product of an integral 2 ×2 matrix A with the incidence matrix of a complete graph. We give a compact expression for the least common multiple of the subdeterminants of this product matrix, generalized to A of order m × 2. 2. Background Kronecker product. For matrices A =(aij)m×k and B =(bij)n×l, the Kronecker product A⊗B is defined to be the mn×kl block matrix a11B ··· a1kB . . .. . am1B ··· amkB It is known (see [2], for example) that when A and B are square matri- ces of orders m and n, respectively, then det(A⊗B)=det(A)n det(B)m. 2000 Mathematics Subject Classification. 15A15, 05C50, 15A57. Key words and phrases. Kronecker product, determinant, least common multi- ple, incidence matrix of complete graph, matrix minor.
    [Show full text]
  • Matrix Differential Calculus with Applications to Simple, Hadamard, and Kronecker Products
    JOURNAL OF MATHEMATICAL PSYCHOLOGY 29, 414492 (1985) Matrix Differential Calculus with Applications to Simple, Hadamard, and Kronecker Products JAN R. MAGNUS London School of Economics AND H. NEUDECKER University of Amsterdam Several definitions are in use for the derivative of an mx p matrix function F(X) with respect to its n x q matrix argument X. We argue that only one of these definitions is a viable one, and that to study smooth maps from the space of n x q matrices to the space of m x p matrices it is often more convenient to study the map from nq-space to mp-space. Also, several procedures exist for a calculus of functions of matrices. It is argued that the procedure based on differentials is superior to other methods of differentiation, and leads inter alia to a satisfactory chain rule for matrix functions. c! 1985 Academic Press, Inc 1. INTRODUCTION In mathematical psychology (among other disciplines) matrix calculus has become an important tool. Several definitions are in use for the derivative of a matrix function F(X) with respect to its matrix argument X (see Dwyer & MacPhail, 1948; Dwyer, 1967; Neudecker, 1969; McDonald & Swaminathan, 1973; MacRae, 1974; Balestra, 1976; Nel, 1980; Rogers, 1980; Polasek, 1984). We shall see that only one of these definitions is appropriate. Also, several procedures exist for a calculus of functions of matrices. We shall argue that the procedure based on differentials is superior to other methods of differentiation. These, then, are the two purposes of this paper. We have been inspired to write this paper by Bentler and Lee’s (1978) note.
    [Show full text]
  • Hadamard, Khatri-Rao, Kronecker and Other Matrix Products
    INTERNATIONAL JOURNAL OF °c 2008 Institute for Scienti¯c INFORMATION AND SYSTEMS SCIENCES Computing and Information Volume 4, Number 1, Pages 160{177 HADAMARD, KHATRI-RAO, KRONECKER AND OTHER MATRIX PRODUCTS SHUANGZHE LIU AND GOTZÄ TRENKLER This paper is dedicated to Heinz Neudecker, with a®ection and appreciation Abstract. In this paper we present a brief overview on Hadamard, Khatri- Rao, Kronecker and several related non-simple matrix products and their prop- erties. We include practical applications, in di®erent areas, of some of the al- gebraic results. Key Words. Hadamard (or Schur) product, Khatri-Rao product, Tracy- Singh product, Kronecker product, vector cross product, positive de¯nite vari- ance matrix, multi-way model, linear matrix equation, signal processing. 1. Introduction Matrices and matrix operations are studied and applied in many areas such as engineering, natural and social sciences. Books written on these topics include Berman et al. (1989), Barnett (1990), LÄutkepohl (1996), Schott (1997), Magnus and Neudecker (1999), Hogben (2006), Schmidt and Trenkler (2006), and espe- cially Bernstein (2005) with a number of referred books classi¯ed as for di®erent areas in the preface. In this paper, we will in particular overview briefly results (with practical applications) involving several non-simple matrix products, as they play a very important role nowadays and deserve to receive such attention. The Hadamard (or Schur) and Kronecker products are studied and applied widely in matrix theory, statistics, system theory and other areas; see, e.g. Styan (1973), Neudecker and Liu (1995), Neudecker and Satorra (1995), Trenkler (1995), Rao and Rao (1998), Zhang (1999), Liu (2000a, 2000b) and Van Trees (2002).
    [Show full text]
  • Clifford Algebra Calculations with Representation Theory & An
    Clifford Algebra Calculations with Representation Theory & an Introduction to Clifford Algebra A Senior Project presented to the Faculty of the Aerospace Engineering Department California Polytechnic State University, San Luis Obispo In Partial Fulfillment of the Requirements for the Degree Bachelor of Science by Alexander I. Scherling August, 2011 ©2011 Scherling, Alexander I. Clifford Algebra Calculations with Representation Theory & an Introduction to Clifford Algebra Alexander I. Scherling* California Polytechnic State University, San Luis Obispo, CA, 93407 The goals of this paper are to provide an introduction to vector, exterior and Clifford algebra and to present a method for performing Clifford algebra calculations efficiently using representation theory. Vectors, exterior algebra and other mathematical and historical foundations of Clifford algebra are introduced. Matrix representations of Clifford algebras are elucidated. The computation of rotations using Clifford representations of spin groups is discussed, and a few of the relevant scientific and engineering applications of the Clifford and exterior algebras are noted throughout. I. Introduction to Vectors and Exterior Algebra One of the most fundamental ideas used in the study of linear algebra and geometry is the concept of a vector. A vector is defined as an element of a vector space. A definition of a vector space adapted from one given by Kreyzig1 is as follows: a vector space is a nonempty set V of vectors with the same number of components such that any two vectors a and b in V and all their linear combinations aα + bβ (where α and β are scalars, defined as elements of a field F) are elements of V, and these vectors satisfy the rules of vector addition and scalar multiplication.
    [Show full text]