Mathematics and Its History
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Unaccountable Numbers
Unaccountable Numbers Fabio Acerbi In memoriam Alessandro Lami, a tempi migliori HE AIM of this article is to discuss and amend one of the most intriguing loci corrupti of the Greek mathematical T corpus: the definition of the “unknown” in Diophantus’ Arithmetica. To do so, I first expound in detail the peculiar ter- minology that Diophantus employs in his treatise, as well as the notation associated with it (section 1). Sections 2 and 3 present the textual problem and discuss past attempts to deal with it; special attention will be paid to a paraphrase contained in a let- ter of Michael Psellus. The emendation I propose (section 4) is shown to be supported by a crucial, and hitherto unnoticed, piece of manuscript evidence and by the meaning and usage in non-mathematical writings of an adjective that in Greek math- ematical treatises other than the Arithmetica is a sharply-defined technical term: ἄλογος. Section 5 offers some complements on the Diophantine sign for the “unknown.” 1. Denominations, signs, and abbreviations of mathematical objects in the Arithmetica Diophantus’ Arithmetica is a collection of arithmetical prob- lems:1 to find numbers which satisfy the specific constraints that 1 “Arithmetic” is the ancient denomination of our “number theory.” The discipline explaining how to calculate with particular, possibly non-integer, numbers was called in Late Antiquity “logistic”; the first explicit statement of this separation is found in the sixth-century Neoplatonic philosopher and mathematical commentator Eutocius (In sph. cyl. 2.4, in Archimedis opera III 120.28–30 Heiberg): according to him, dividing the unit does not pertain to arithmetic but to logistic. -

15 Famous Greek Mathematicians and Their Contributions 1. Euclid
15 Famous Greek Mathematicians and Their Contributions 1. Euclid He was also known as Euclid of Alexandria and referred as the father of geometry deduced the Euclidean geometry. The name has it all, which in Greek means “renowned, glorious”. He worked his entire life in the field of mathematics and made revolutionary contributions to geometry. 2. Pythagoras The famous ‘Pythagoras theorem’, yes the same one we have struggled through in our childhood during our challenging math classes. This genius achieved in his contributions in mathematics and become the father of the theorem of Pythagoras. Born is Samos, Greece and fled off to Egypt and maybe India. This great mathematician is most prominently known for, what else but, for his Pythagoras theorem. 3. Archimedes Archimedes is yet another great talent from the land of the Greek. He thrived for gaining knowledge in mathematical education and made various contributions. He is best known for antiquity and the invention of compound pulleys and screw pump. 4. Thales of Miletus He was the first individual to whom a mathematical discovery was attributed. He’s best known for his work in calculating the heights of pyramids and the distance of the ships from the shore using geometry. 5. Aristotle Aristotle had a diverse knowledge over various areas including mathematics, geology, physics, metaphysics, biology, medicine and psychology. He was a pupil of Plato therefore it’s not a surprise that he had a vast knowledge and made contributions towards Platonism. Tutored Alexander the Great and established a library which aided in the production of hundreds of books. -

Fiboquadratic Sequences and Extensions of the Cassini Identity Raised from the Study of Rithmomachia
Fiboquadratic sequences and extensions of the Cassini identity raised from the study of rithmomachia Tom´asGuardia∗ Douglas Jim´enezy October 17, 2018 To David Eugene Smith, in memoriam. Mathematics Subject Classification: 01A20, 01A35, 11B39 and 97A20. Keywords: pythagoreanism, golden ratio, Boethius, Nicomachus, De Arithmetica, fiboquadratic sequences, Cassini's identity and rithmomachia. Abstract In this paper, we introduce fiboquadratic sequences as a consequence of an extension to infinity of the board of rithmomachia. Fiboquadratic sequences approach the golden ratio and provide extensions of Cassini's Identity. 1 Introduction Pythagoreanism was a philosophical tradition, that left a deep influence over the Greek mathematical thought. Its path can be traced until the Middle Ages, and even to present. Among medieval scholars, which expanded the practice of the pythagoreanism, we find Anicius Manlius Severinus Boethius (480-524 A.D.) whom by a free translation of De Institutione Arithmetica by Nicomachus of Gerasa, preserved the pythagorean teaching inside the first universities. In fact, Boethius' book became the guide of study for excellence during quadriv- ium teaching, almost for 1000 years. The learning of arithmetic during the arXiv:1509.03177v3 [math.HO] 22 Nov 2016 quadrivium, made necessary the practice of calculation and handling of basic mathematical operations. Surely, with the mixing of leisure with this exercise, Boethius' followers thought up a strategy game in which, besides the training of mind calculation, it was used to preserve pythagorean traditions coming from the Greeks and medieval philosophers. Maybe this was the origin of the philoso- phers' game or rithmomachia. Rithmomachia (RM, henceforward) became the ∗Department of Mathematics. -

Hypatia of Alexandria A. W. Richeson National Mathematics Magazine
Hypatia of Alexandria A. W. Richeson National Mathematics Magazine, Vol. 15, No. 2. (Nov., 1940), pp. 74-82. Stable URL: http://links.jstor.org/sici?sici=1539-5588%28194011%2915%3A2%3C74%3AHOA%3E2.0.CO%3B2-I National Mathematics Magazine is currently published by Mathematical Association of America. Your use of the JSTOR archive indicates your acceptance of JSTOR's Terms and Conditions of Use, available at http://www.jstor.org/about/terms.html. JSTOR's Terms and Conditions of Use provides, in part, that unless you have obtained prior permission, you may not download an entire issue of a journal or multiple copies of articles, and you may use content in the JSTOR archive only for your personal, non-commercial use. Please contact the publisher regarding any further use of this work. Publisher contact information may be obtained at http://www.jstor.org/journals/maa.html. Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission. The JSTOR Archive is a trusted digital repository providing for long-term preservation and access to leading academic journals and scholarly literature from around the world. The Archive is supported by libraries, scholarly societies, publishers, and foundations. It is an initiative of JSTOR, a not-for-profit organization with a mission to help the scholarly community take advantage of advances in technology. For more information regarding JSTOR, please contact [email protected]. http://www.jstor.org Sun Nov 18 09:31:52 2007 Hgmdnism &,d History of Mdtbenzdtics Edited by G. -

Did Hypatia Know About Negative Numbers?
Did Hypatia Know about Negative Numbers? Hypatia lived in Alexandria in the 4th-5th century AD. She was one of the most remarkable women in history. Her father Theon, presumably the last member of the Museum, instructed her in mathematics, philosophy and clas- sical Greek literature. With time she herself became a brilliant teacher of Neoplatonic philosophy and mathematics. Numerous young aspirants from wealthy Christian and pagan families came to Alexandria with the sole pur- pose of joining the sophisticated inner circle of her students. Theon and Hyptia edited several of the major mathematical treatises avail- able in their time: Arithmetica by Diophantus, Almagest by Ptolemy, Conics by Appolonius of Perga, and Elements by Euclid. A significant part of this work, in particular on the most difficult and demanding Arithmetica, she did alone. To some of these treatises she added commentaries and exemplary exercises. A charismatic figure in the city’s intellectual life and a close friend to many important officials, Hypatia had a significant influence on the Alexandrian elite and politics. She was admired for her knowledge, wisdom, righteousness and personal charm. Her public lectures for the Alexandrian intelligentsia attracted a great deal of interest. However, her elevated social position and popularity did not prevent her from becoming the victim of a brutal murder in 415 AD by the fanatic mob who accused her of conducting forbidden magical practices. Groundless rumors about Hypatia’s dealings with witchcraft were most likely inspired by her political enemies. Bishop Cyril was certainly one of them, but the allegations concerning his direct involvement have never been proven. -

The Meaning of ''Plasmatikon'' in Diophantus' ''Arithmetica''
The meaning of ”plasmatikon” in Diophantus’ ”Arithmetica”. Fabio Acerbi To cite this version: Fabio Acerbi. The meaning of ”plasmatikon” in Diophantus’ ”Arithmetica”.. Archive for History of Exact Sciences, Springer Verlag, 2009, 63, pp. 5-31. 10.1007/s00407-008-0028-8. halshs-00346121 HAL Id: halshs-00346121 https://halshs.archives-ouvertes.fr/halshs-00346121 Submitted on 29 Apr 2010 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Archive for History of Exact Sciences 63 (2009), 5-31 The Meaning of plasmatikovn in Diophantus’ Arithmetica FABIO ACERBI 1 Introduction Diophantus’ Arithmetica is an idiosyncratic treatise: it almost calls for interpretations that force conceptions into the text that are extraneous to the by-and-large ineffable aims of its author. A case in point is constituted by a short clause found in three problems of book I.1 It is not a harmless clause: it contains the elusive adjective plasmatikovn as the crucial word, the translation and meaning of which sparked a long-lasting controversy that has become a non- negligible aspect of the debate about the possibility of interpreting Diophantus’ approach and, more generally, Greek mathematics in algebraic terms.2 The whole interpretative controversy is in fact entangled. -

The Generalized Principle of the Golden Section and Its Applications in Mathematics, Science, and Engineering
Chaos, Solitons and Fractals 26 (2005) 263–289 www.elsevier.com/locate/chaos The Generalized Principle of the Golden Section and its applications in mathematics, science, and engineering A.P. Stakhov International Club of the Golden Section, 6 McCreary Trail, Bolton, ON, Canada L7E 2C8 Accepted 14 January 2005 Abstract The ‘‘Dichotomy Principle’’ and the classical ‘‘Golden Section Principle’’ are two of the most important principles of Nature, Science and also Art. The Generalized Principle of the Golden Section that follows from studying the diagonal sums of the Pascal triangle is a sweeping generalization of these important principles. This underlies the foundation of ‘‘Harmony Mathematics’’, a new proposed mathematical direction. Harmony Mathematics includes a number of new mathematical theories: an algorithmic measurement theory, a new number theory, a new theory of hyperbolic functions based on Fibonacci and Lucas numbers, and a theory of the Fibonacci and ‘‘Golden’’ matrices. These mathematical theories are the source of many new ideas in mathematics, philosophy, botanic and biology, electrical and computer science and engineering, communication systems, mathematical education as well as theoretical physics and physics of high energy particles. Ó 2005 Elsevier Ltd. All rights reserved. Algebra and Geometry have one and the same fate. The rather slow successes followed after the fast ones at the beginning. They left science at such step where it was still far from perfect. It happened,probably,because Mathematicians paid attention to the higher parts of the Analysis. They neglected the beginnings and did not wish to work on such field,which they finished with one time and left it behind. -

Hypatia of Alexandria Anne Serban
Hypatia of Alexandria Anne Serban Hypatia's Life Hypatia of Alexandria was born sometime between the years 350 to 370 AD in Alexandria of Egypt. She was the only daughter of Theon of Alexandria; no information exists about her mother. "Hypatia may have had a brother, Epiphanius, though he may have been only Theon's favorite pupil." Theon did not want to force his daughter to become the typical woman described by historian Slatkin when he wrote "Greek women of all classes were occupied with the same type of work, mostly centered around the domestic needs of the family. Women cared for young children, nursed the sick, and prepared food." Instead he educated her in math, astronomy and philosophy, as well as in different religions. Theons desire that his daughter be different from the mold that society created for women influenced the rest of Hypatias life. Eventually Hypatia became a teacher herself. She instructed her pupils, who were both pagans and Christians, in math, astronomy, and philosophy, focusing mostly on Neoplatonism. She also held lectures on various topics, often drawing many eager listeners. Her greatest contributions benefitted the fields of mathematics and astronomy. By 400 AD, she became the head of the Platonist school in Alexandria. "Hypatia, on the other hand, led the life of a respected academic at Alexandria's university; a position to which, as far as the evidence suggests, only males were entitled previously." Hypatia took many of Platos ideas as personal applications, choosing even to live a life of celibacy. Furthermore, Hypatia wrote three commentaries and worked with Theon on several books. -

On the Shoulders of Hipparchus a Reappraisal of Ancient Greek Combinatorics
Arch. Hist. Exact Sci. 57 (2003) 465–502 Digital Object Identifier (DOI) 10.1007/s00407-003-0067-0 On the Shoulders of Hipparchus A Reappraisal of Ancient Greek Combinatorics F. Acerbi Communicated by A. Jones 1. Introduction To write about combinatorics in ancient Greek mathematics is to write about an empty subject. The surviving evidence is so scanty that even the possibility that “the Greeks took [any] interest in these matters” has been denied by some historians of mathe- matics.1 Tranchant judgments of this sort reveal, if not a cursory scrutiny of the extant sources, at least a defective acquaintance with the strong selectivity of the process of textual transmission the ancient mathematical corpus has been exposed to–afactthat should induce, about a sparingly attested field of research, a cautious attitude rather than a priori negative assessments.2 (Should not the onus probandi be required also when the existence in the past of a certain domain of research is being denied?) I suspect that, behind such a strongly negative historiographic position, two different motives could have conspired: the prejudice of “ancient Greek mathematicians” as geometri- cally-minded and the attempt to revalue certain aspects of non-western mathematics by tendentiously maintaining that such aspects could not have been even conceived by “the Greeks”. Combinatorics is the ideal field in this respect, since many interesting instances of combinatorial calculations come from other cultures,3 whereas combina- torial examples in the ancient Greek mathematical corpus have been considered, as we have seen, worse than disappointing, and in any event such as to justify a very negative attitude. -

5. the Late Greek Period
5. The late Greek period (Burton, 5.1 – 5.4 ) During the period between 400 B.C.E. and 150 B.C.E., Greek mathematical knowledge had increased very substantially . Over the next few centuries , progress was more limited , and much of it involved mathematical topics like trigonometry that were needed in other subjects such as astronomy . However , shortly before the end of the ancient Greek period during the 6th century A.D. there was some resurgence of activity that had important , far – reaching consequences for the future . During this period several writers also summarized numerous earlier works that are now (presumably) lost , and a large part of our present knowledge of Greek mathematics is derived from these summaries . Diophantus of Alexandria The known information about Diophantus (conjecturally 200 – 284 , but possibly these years should be shifted by two decades or more) is contained in a classic algebraic word problem that is reproduced on page 218 of Burton . His most important work is contained in his Arithmetica , of which we now have the first six out of thirteen books ; manuscripts claiming to be later books from this work have been discovered but their authenticity has not been established . The Arithmetica of Diophantus differed greatly from earlier Greek writings in its treatment of purely algebraic problems in purely algebraic terms ; as noted earlier , even the simplest algebraic equations had been analyzed in geometrical terms ever since the Pythagorean ’s discovery of irrational numbers . Two aspects of Arithmetica are particularly noteworthy : One is his consideration of equations that have (usually infinitely) many solutions over the rational numbers or integers , and another is his introduction of special notation to manipulate mathematical relationships . -
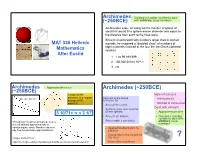
Archimedes (~250BCE) (~250BCE) Computed the Ideas of Calculus Perimeter of a Regular BD : CD = BA : AC
Archimedes Created a number system to deal (~250BCE) with arbitrary large numbers Archimedes wrote an essay on the number of grains of sand that would fill a sphere whose diameter was equal to the distance from earth to the fixes stars. Since he had to work with numbers larger than in myriad MAT 336 Hellenic myriads, he imagined a “doubled class” of numbers of eight numerals (instead of the four the the Greek ciphered Mathematics system) After Euclid 1. 1 to 99,999,999 2. 100,000,000 to 1016-1 3. etc Archimedes Approximation of π Archimedes (~250BCE) (~250BCE) Computed the Ideas of calculus perimeter of a regular BD : CD = BA : AC. Derived and proved Infinitesimals polygon of 96 formulae for Method of exhaustion sides!!!!!! Area of the circle Dealt with infinity!!! Surface area and volume 3 10/71< π < 3 1/7 of the sphere Approximation of π Area of an ellipse. Created a number system to deal with Throughout this proof, Archimedes uses Area under a parabola arbitrary large several rational approximations to numbers various square roots. Nowhere does he Applied mathematics to say how he got those approximations. physics Explanation of principle of ? Images and text from: the lever https://itech.fgcu.edu/faculty/clindsey/mhf4404/archimedes/archimedes.html Innovative machines Archimedes (~250BCE) Archimedes Archimedes (~250BCE) (~250BCE) http://abel.math.harvard.edu/~knill//3dprinter/documents/paper.pdf Proposition 33: The surface of any sphere is equal to four times the circle in it. Proposition 34: Any sphere is equal to four times the cone -

The Beginnings of Greek Mathematics Greeks Were Not Confined to A
Chapter 3: The Beginnings of Greek Mathematics Greeks were not confined to a neighborhood or the Aegean and the Peloponnesis. They ranged far and wide including present day Italy and Sicily and many lived in North Africa including Egypt. This is of course before the expansion of the Roman Empire (Punic Wars, 3rd Century B.C. and the Second Punic War was 218-201 B.C.) The Greeks introduced abstraction and gave logical arguments. For example Greeks were interested in triangles and not simply triangular fields. Thales of Miletus (ca. 625-547) (Miletus is in Asia Minor). Thales is sometimes known as the father of geometry probably because he was the first to use the deductive method. He proved among other things (see page 83 of the text) that a triangle inscribed inside a semi-circle (with one side the diameter) must be a right triangle. He also observed that the sides similar triangles are proportional. We do not have any mathematical works directly attributable to Thales or Pythagoras. Euclid’s Elements (Euclid 323-285) and Nicomachus of Gerasa’s Introductio Arithmeticae written ca. 100 B.C. are two math texts which we depend on but neither gives credit to the originators and discoverers of the results. Introductio Arithmeticae unlike Elements was a popular textbook for teaching geometry. Thales is credited with using similar triangles to discover the height of a the Great Pyramid of Gizeh (2600 B.C.) He similarly estimated distance to a ship offshore from a tower above the shore. See page 84 of the text. Pythagoras of Samos (580-500 B.C.; or 569-475 B.C.) (Samos is an Island in the northern Aegean near Asia Minor) His father was given honorary citizenship for bringing corn (!) in a time of famine.