DOCSLIB.ORG

Macroeconomic Measurements Cost of Living Calculating the Rate of Inflation Page 1 of 3

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Macroeconomic Measurements Cost of Living Calculating the Rate of Inflation Page 1 of 3 Macroeconomic Measurements Cost of Living Calculating the Rate of Inflation Page 1 of 3 Now, here’s a mystery. On page one of the Wall Street Journal, the inflation rate is reported at 2.5%, and on page fourteen of the same day’s journal it says we’ve had 0% inflation for the last year. Now, how can both of these numbers be correct? Is there an error or is there something I’m missing? Hold on, on page one it says that the 2.5% inflation rate is based on the GDP deflator; whereas, on page fourteen in says that the 0% inflation rate is based on the consumer price index. Now, I know that these two indexes are different, and maybe that accounts for the difference in their measures of inflation. After all, the consumer price index measures only the prices of a subset of goods – goods that are purchased regularly by households, things like food and clothing – whereas, the GDP deflator includes all of the goods and services produced in the economy. So, since the consumer price index is based on the prices of fewer goods maybe that’s why the number is different than the inflation rate measured by the GDP deflator. However, it turns out that there’s something else going on. What’s going on is that even if the GDP deflator and the consumer price index were based on exactly the same set of goods, you could get different numbers because of differences in the way in which the two indexes are calculated. I think I can make this point very clear with a simple example. Consider an economy that produces only two goods, food and clothing. We’re choosing food and clothing because these are goods that consumers purchase, so the consumer price index is based on the price of these goods, and since these are the only goods produced in the economy, the GDP deflator depends also only on the price of these two goods. Now let’s look at the gross domestic product data for two consecutive years, the year 2000 and the year 2001. In the year 2000, ten units of food are produced, and the price per unit is $10 for food. So, $10 times ten units is $100 worth of food production. Clothing: $20 per unit times ten units is $200 from clothing production. $200 plus $100 gives us a gross domestic product of $300 in the year 2000. Now, as we move to the year 2001, notice that two things have changed. First, the prices of goods have changed. Food is now selling for $20 a unit and clothing for $35 a unit. The next thing that’s changed is that quantities have changed. There’s more food produced and more clothing produced, so the gross domestic product is going to be larger because prices are bigger and quantities are bigger. Let’s go ahead and calculate the gross domestic product for the year 2001. $20 per unit of food times fifteen units of food gives us a GDP from food of $300. Over here under clothing, we’ve got $35 a unit times fifteen units for $525 worth of clothing produced. $525 plus $300 gives us a gross domestic product for the year 2001 of 825. Now, I’m interested in what’s happening to prices between the year 2000 and the year 2001. Now, since there are two different goods being produced, our overall measure of prices has got to be some kind of weighted average of the change in prices, and the way in which that weighted average is calculated is what distinguishes the consumer price index from the GDP deflator. Let’s look first at the method used in calculating the consumer price index. The intuition behind a consumer price index is how much would you have to pay to get the same goods you got last year at this year’s prices, so we’re using the quantities from last year but the prices from this year. Let’s look, then, at how the consumer price index is calculated. Macroeconomic Measurements Cost of Living Calculating the Rate of Inflation Page 2 of 3 The question is what would it cost you to buy last years goods at this years prices? So, let’s look first, then, at that amount of money that you’d have to spend. What I’m going to do is take the quantities from the year 2000 and move them forward to the year 2001 and calculate the spending I would have to do at 2001 prices in order to buy the year 2000 quantities. So, in the year 2001, food is now $20 a unit, $20 a unit times the original ten units of food that we were buying last year is $200 you’re going to have to spend to get the same food that you were buying last year. What about clothing? Last year you had ten units of clothing so this year when you have to pay $35 a unit for clothing, you’re going to have to spend $350 to get the same amount of clothing that you had last year. So, $350 on clothing, $200 on food gives us a grand total of $550 that you have to spend in the year 2001 when prices are higher to get the same goods that you were buying back in the year 2000. Now, let’s calculate the consumer price index. The consumer price index is a ratio. It’s a ratio of the amount of money that you’d have to spend this year to get that basket relative to how much you have to spend in the base year, the year whose quantities you’re considering. So, let’s calculate, $550, the amount we’d have to spend in the year 2001, divided by $300, the amount we had to spend in our base year, the year 2000, multiply that by one hundred and you get the consumer price index, which in this case is 183. So, the consumer price index for the year 2001 is 183. That’s the amount by which prices have increased from one year to the next, but we’re interested in percentage increase, the amount by which prices have increased in percentage terms because that’s the inflation rate. So, what we do to calculate the inflation rate using this method is we take the consumer price index for the year 2001, and we subtract from it the consumer price index from the year 2000. Now, the year 2000 is our base year, remember, where it costs $300 to buy that basket of goods and services. So, divide $300, which is the amount you have to spend in the year 2000, by $300, which is the amount you have to spend in the base year, and you get one hundred. The CPI for the base year by definition is always 100%, it’s equal to itself. So, subtract 100 from 183. So, this is the CPI for the year 2001 minus the CPI for the year 2000, the base year. And divide by the base year amount which is 100, and that’s going to give us the rate of inflation. One hundred eighty three minus 100 is 83 divided by 100 is equal to 83%. The rate of inflation measured according to the method of the CPI is 83%. The CPI has increased by 83% from the year 2000 to the year 2001. The price of that market basket of goods and services has gone up by 83%; that’s the inflation rate measured with this method. Now, let’s look at the other method for calculating the inflation rate. This one is based on the GDP deflator. Remember, the GDP deflator is the ratio between the nominal GDP in a particular year and the real GDP for that same year. The way you calculate the real GDP, you’ll remember, is to find the value of the goods and services produced in a particular year using the market prices from the base year. So, the nominal GDP for the year 2001 is 550, but the real GDP is calculated using the year 2000 prices. So, let’s go ahead and put the year 2000 prices into our equation and use the year 2001 quantities. So, this means that the real GDP for the year 2001 is $10 times fifteen units of food or $150, plus $20 times fifteen units of clothing worth $300. $300 plus $150 gives us a real gross domestic product of $450. Now, to find the GDP deflator take the nominal GDP and divide by the real GDP, and this should give us, then, after we multiply by 100, some notion of on average how much prices have risen between the year 2000 and the year 2001. And the answer is 122. So, 122 is the GDP deflator for the year 2001. Macroeconomic Measurements Cost of Living Calculating the Rate of Inflation Page 3 of 3 To calculate the inflation rate, now, we have to see how the GDP deflator has changed between the two years. So, we now want to do a percentage change calculation. So, let’s do that. 122 is the GDP deflator for the year 2001. What’s the year 2000 GDP deflator? Well, it’s the base year. So, in the base year the GDP deflator is always going to be 100% because you’re comparing that year with itself. So, subtract 100 from 122 and divide by 100 and that’s going to give us an inflation rate of 22%.
Load more

Recommended publications
  • THE ESSENTIAL MACROECONOMIC AGGREGATES Chapter 1
    Chapter 1 THE ESSENTIAL MACROECONOMIC AGGREGATES 1. Gross Domestic Product (GDP) 2. “Real” GDP and GDP deflator 3. Investment and consumption 4. A first macroeconomic reconciliation 5. The second macroeconomic reconciliation 1 THE ESSENTIAL MACROECONOMIC AGGREGATES CHAPTER 1 The Essential Macroeconomic Aggregates In this first chapter, our aim is to give an initial definition of the essential macroeconomic variables, listed in the table below, and taken from the I. Each chapter of this OECD Economic Outlook for December 2004.1 We have chosen to book uses an example from illustrate this chapter using the example of Germany, but we might as well a different country. have chosen any other OECD country, since the structure of the country chapters in the OECD Economic Outlook is the same for all countries. X I. Table 1. Main macroeconomic variables Germany,a 1995 euros, annual changes in percentage 2002 2003 2004 2005 2006 Private consumption –0.7 0.0 –0.7 0.8 1.9 Gross capital formation –6.3 –2.2 –2.0 0.6 3.4 GDP 0.1 –0.1 1.2 1.4 2.3 Imports –1.6 3.9 6.4 4.9 7.5 Exports 4.1 1.8 8.1 5.7 8.1 Household saving ratio1 10.5 10.7 11.1 11.1 10.8 GDP deflator 1.5 1.1 0.9 0.8 0.9 General government financial balance2 –3.7 –3.8 3.9 –3.5 –2.7 1. Net saving as % of net disposable income. 2. % of GDP. a) The report dates from December 2004.
    [Show full text]
  • IIF Database Glossary
    The Institute of International Finance Glossary for IIF Economic Databases Definitions for Downloadable Codes January 2019 3 Table of Contents I. NATIONAL ACCOUNTS AND EMPLOYMENT .................................................... 3 A. GDP AT CONSTANT PRICES .......................................................................................... 3 1. Expenditure Basis .................................................................................................... 3 2. Output Basis ............................................................................................................. 4 3. Hydrocarbon Sector ................................................................................................. 5 B. GDP AT CURRENT PRICES ............................................................................................ 6 C. GDP DEFLATORS.......................................................................................................... 8 D. INVESTMENT AND SAVING ............................................................................................ 9 E. EMPLOYMENT AND EARNINGS ...................................................................................... 9 II. TRADE AND CURRENT ACCOUNT ..................................................................... 11 A. CURRENT ACCOUNT ................................................................................................... 11 B. TERMS OF TRADE ....................................................................................................... 14 III.
    [Show full text]
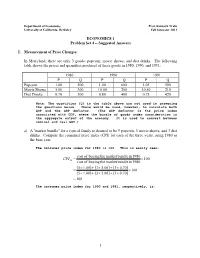
  • Suggested Answers I. Measurement of Price Changes. in Merryland, There
    Department of Economics Prof. Kenneth Train University of California, Berkeley Fall Semester 2011 ECONOMICS 1 Problem Set 4 -- Suggested Answers I. Measurement of Price Changes. In Merryland, there are only 3 goods: popcorn, movie shows, and diet drinks. The following table shows the prices and quantities produced of these goods in 1980, 1990, and 1991: 1980 1990 1991 P Q P Q P Q Popcorn 1.00 500 1.00 600 1.05 590 Movie Shows 5.00 300 10.00 200 10.50 210 Diet Drinks 0.70 300 0.80 400 0.75 420 Note: The quantities (Q) in the table above are not used in answering the questions below. These would be used, however, to calculate both GDP and the GDP deflator. (The GDP deflator is the price index associated with GDP, where the bundle of goods under consideration is the aggregate output of the economy. It is used to convert between nominal and real GDP.) a) A "market bundle" for a typical family is deemed to be 5 popcorn, 3 movie shows, and 3 diet drinks. Compute the consumer price index (CPI) for each of the three years, using 1980 as the base year. The consumer price index for 1980 is 100. This is easily seen: cost of buying the market bundle in 1980 CPI = ×100 80 cost of buying the market bundle in 1980 ()()()5 ×1.00 + 3× 5.00 + 3× 0.70 = ×100 ()()()5 ×1.00 + 3× 5.00 + 3× 0.70 =100 The consumer price index for 1990 and 1991, respectively, is: 1 cost of buying the market bundle in 1990 CPI = ×100 90 cost of buying the market bundle in 1980 ()()()5 ×1.00 + 3×10.00 + 3× 0.80 = ×100 ()()()5 ×1.00 + 3× 5.00 + 3× 0.70 =169.2 cost of buying the market bundle in 1991 CPI = ×100 91 cost of buying the market bundle in 1980 ()()()5 ×1.05 + 3×10.50 + 3× 0.75 = ×100 ()()()5 ×1.00 + 3× 5.00 + 3× 0.70 =176.5 b) What was the rate of inflation from 1990 to 1991, using the CPI you calculated in (a)? The rate of inflation equals the percentage change in the price index from 1990 to 1991.
    [Show full text]
  • The Big Mac Index: a Shortcut to Inflation and Exchange Rate
    CORE Metadata, citation and similar papers at core.ac.uk Provided by Clute Institute: Journals International Business & Economics Research Journal – July/August 2014 Volume 13, Number 4 The Big Mac Index: A Shortcut To Inflation And Exchange Rate Dynamics? Price Tracking And Predictive Properties Luis San Vicente Portes, Montclair State University, USA Vidya Atal, Montclair State University, USA ABSTRACT The Economist magazine has been publishing the Big Mac Index using it as a rule of thumb to determine the over- or under-valuation of international currencies based on the theory of Purchasing Power Parity since 1986. According to the theory, using the Big Mac as a tradable single-good basket, the Dollar-value of the hamburger should be equalized around the world due to arbitrage. The popularity and following of the Big Mac Index led the authors to the following two questions: 1) How effective is the Big Mac price as an indicator of overall inflation? and 2) how accurate are exchange rate movement predictions based on Big Mac prices? They find that Big Mac prices tend to lag overall inflation rates, which is highly important in studies that use Big Mac prices as measures of affordability or real incomes over time. As a guide to exchange rate movements, there is support for the theory of Purchasing Power Parity, but only as a qualitative indicator of movement in the nominal exchange rate in rich and economically stable countries, proving less effective in forecasting exchange rate movements in emerging markets. The statistical analysis is carried out using data from 1986 to 2012 from The Economist and from the World Bank for 54 countries.
    [Show full text]
  • Price Indices and Real Versus Nominal Values
    Price Indices and Real versus Nominal Values Real verse Nominal Values Prices in an economy do not stay the same. Over time the price level changes (i.e., there is inflation or deflation). A change in the price level changes the value of economic measures denominated in dollars. Values that increase or decrease with price level are called nominal values. Real values are adjusted for price changes. That is, they are calculated as though prices did not change from the base year. For example, gross domestic product (GDP) is used to measure fluctuations in output. However, since GDP is the dollar value of goods and services produced in the economy, it increases when prices increase. This means that nominal GDP increases with inflation and decreases with deflation. But when GDP is used as a measure of short-run economic growth, we are interested in measuring performance—real GDP takes out the effects of price changes and allows us to isolate changes in output. Price indices are used to adjust for price changes. They are used to convert nominal values into real values. Converting Nominal GDP to Real GDP To use GDP to measure output growth, it must be converted from nominal to real. Let’s say nominal GDP in Year 1 is $1,000 and in Year 2 it is $1,100. Does this mean the economy has grown 10 percent between Year 1 and Year 2? Not necessarily. If prices have risen, part of the increase in nominal GDP for Year 2 will represent the increase in prices. GDP that has been adjusted for price changes is called real GDP.
    [Show full text]
  • Using Price Indexes
    INFORMATION BRIEF Research Department Minnesota House of Representatives 600 State Office Building St. Paul, MN 55155 Pat Dalton, Legislative Analyst, 651-296-7434 Kathy Novak, Legislative Analyst, 651-296-9253 Updated: November 2009 Using Price Indexes This information brief is a nontechnical guide to the use of price indexes. It explains the difference among the three most commonly used price indexes and suggests when each index should be used. Additionally, this information brief shows how to make some common calculations using price indexes. Contents Price Indexes and Their Uses ...........................................................................................................2 Descriptions of the Major Price Indexes ..........................................................................................2 Gross Domestic Product Chain-Weighted Price Index ..............................................................2 Consumer Price Index (CPI) ......................................................................................................4 Producer Price Index (PPI) ........................................................................................................5 Glossary of Price Index Terms ........................................................................................................7 Common Calculations Using Price Indexes ....................................................................................8 Summary of Major Price Indexes ..................................................................................................10
    [Show full text]
  • Taking the Nation's Economic Pulse
    CHAPTER 7 Taking the Nation’s Economic Pulse CHAPTER FOCUS ● What is GDP? How is GDP calculated? ● When making comparisons over time, why is it impor- tant to adjust nominal GDP for the effects of inflation? It has been said that figures rule ● What do price indexes measure? How can they be used the world; maybe. I am quite to adjust for changes in the general level of prices? sure that it is figures which show ● us whether it is being ruled well Is GDP a good measure of output? What are its strengths and weaknesses? or badly. —Johann Wolfgang Goethe, 1830 Measurement is the making of distinction; precise measurement is making sharp distinctions. —Enrico Fermi1 1As quoted by Milton Friedman in Economic Freedom: Toward a Theory of Measurement, edited by Walter Block (Vancouver, British Columbia: The Fraser Institute, 1991), 11. ur society likes to keep score. The sports pages supply us with the win–loss records that reveal how well the various teams are doing. We also keep score on the performance of our economy. The scoreboard for economic performance is the national-income accounting system. Just as a firm’s Oaccounting statement provides information on its performance, national-income accounts supply performance information for the entire economy. Simon Kuznets, the winner of the 1971 Nobel Prize in economics, developed the basic concepts of national-income accounting during the 1920s and 1930s (see the Outstanding Economist feature). Through the years, these procedures have been modified and improved. In this chapter, we will explain how the flow of an economy’s output (and income) is measured.
    [Show full text]
  • Adjusting Nominal Values to Real Values (Article) | Khan Academy
    2/11/2019 Adjusting nominal values to real values (article) | Khan Academy Adjusting nominal values to real values Learn how and why we adjust GDP numbers for inflation. Google Classroom Facebook Twitter Email Key points The nominal value of any economic statistic is measured in terms of actual prices that exist at the time. The real value refers to the same statistic after it has been adjusted for inflation. To convert nominal economic data from several different years into real, inflation-adjusted data, the starting point is to choose a base yeararbitrarily and then use a price index to convert the measurements so that they are measured in the money prevailing in the base year. Introduction When we examine economic statistics, it's crucial to distinguish between nominal and real measurements so we know whether or not inflation has distorted a given statistic. Looking at economic statistics without considering inflation is like looking through a pair of binoculars and trying to guess how close something is— unless you know how strong the lenses are, you cannot guess the distance very accurately. Similarly, if you do not know the rate of inflation, it is difficult to figure out if a rise in gross domestic product, or GDP, is due mainly to a rise in the overall level of prices or to a rise in quantities of goods produced. https://www.khanacademy.org/economics-finance-domain/macroeconomics/macro-economic-indicators-and-the-business-cycle/macro-real-vs-nominal… 1/9 2/11/2019 Adjusting nominal values to real values (article) | Khan Academy The nominal value of any economic statistic means the statistic is measured in terms of actual prices that exist at the time.
    [Show full text]
  • Ppps: Purchasing Power Or Producing Power Parities?
    Catalogue no. 11F0027M — No. 058 ISSN 1703-0404 ISBN 978-1-100-13862-6 Research Paper Economic Analysis (EA) Research Paper Series PPPs: Purchasing Power or Producing Power Parities? by John R. Baldwin and Ryan Macdonald Economic Analysis Division 18-F, R.H. Coats Building, 100 Tunney’s Pasture Driveway Telephone: 1-800-263-1136 PPPs: Purchasing Power or Producing Power Parities? by John Baldwin and Ryan Macdonald 11F0027M No. 058 ISSN 1703-0404 ISBN 978-1-100-13862-6 Statistics Canada Economic Analysis Division R.H. Coats Building, 18th floor, 100 Tunney’s Pasture Driveway Ottawa, Ontario K1A 0T6 613-951-8588 E-mail: [email protected] 613-951-5687 E-mail: [email protected] December 2009 Published by authority of the Minister responsible for Statistics Canada © Minister of Industry, 2009 All rights reserved. The content of this electronic publication may be reproduced, in whole or in part, and by any means, without further permission from Statistics Canada, subject to the following conditions: that it be done solely for the purposes of private study, research, criticism, review or newspaper summary, and/or for non-commercial purposes; and that Statistics Canada be fully acknowledged as follows: Source (or “Adapted from,” if appropriate): Statistics Canada, year of publication, name of product, catalogue number, volume and issue numbers, reference period and page(s). Otherwise, no part of this publication may be reproduced, stored in a retrieval system or transmitted in any form, by any means—electronic, mechanical or photocopy—or for any purposes without prior written permission of Licensing Services, Client Services Division, Statistics Canada, Ottawa, Ontario, Canada K1A 0T6.
    [Show full text]
  • Analysis of the Differences Between the Rates of Inflation Associated with Two Aggregate Price Level
    EKONOMIA ETA ENPRESA ZIENTZIEN FAKULTATEA FACULTAD DE CIENCIAS ECONÓMICAS Y EMPRESARIALES Degree in Economics 2014 / 2015 ANALYSIS OF THE DIFFERENCES BETWEEN THE RATES OF INFLATION ASSOCIATED WITH TWO AGGREGATE PRICE LEVEL The case of the euro area and United States Author: Jade Mateo Álvarez Director: Jesús Vázquez Pérez Bilbao, 4 th September 2015. ANALYSIS OF THE DIFFERENCES BETWEEN THE RATES OF INFLATION ASSOCIATED WITH TWO AGGREGATE PRICE LEVEL JADE MATEO ÁLVAREZ INDEX OF CONTENTS 1. INTRODUCTION ................................................................................................................. 1 2. DESCRIPTIVE ANALYSIS ...................................................................................................... 2 The euro area........................................................................................................................ 4 The United States .................................................................................................................. 7 3. ECONOMETRIC ANALYSIS ................................................................................................ 10 The theory of stationary ...................................................................................................... 10 Dickey-Fuller (ADF) .............................................................................................................. 11 Estimation procedure stationary time series ........................................................................ 12 Analysis of the stationarity
    [Show full text]
  • Impact of Cost-Push and Monetary Factors on GDP Deflator: Empirical Evidence from the Economy of Pakistan
    www.sciedu.ca/ijfr International Journal of Financial Research Vol. 2, No. 1; March 2011 Impact of Cost-Push and Monetary Factors on GDP Deflator: Empirical Evidence from the Economy of Pakistan Zahoor Hussain Javed (Corresponding author) Department of Economics, GC University Allama Iqbal Road, Faisalabad, Pakistan Tel: +92-300-650-1785 E-mail: [email protected] Muhammad Farooq Assistant Professor, Department of Sociology, GC University Faisalabad, Pakistan. E-mail:[email protected] Maqsood Hussain Assistant Professor of Agricultural, University of Agricultural Faisalabad, Pakistan. Abdur-Rehman Shezad Lecture in Rural Sociology, University of Agricultural Faisalabad, Pakistan Safder Iqbal Lecturer in Economics, GC University Faisalabad, Pakistan. Shama Akram (Note 1) Department of Economics, GC University Faisalabad, Pakistan Received: August 30, 2010 Accepted: February 11, 2011 doi:10.5430/ijfr.v2n1p57 Abstract The central objective of this paper is to find the validity of cost-push and monetary factors on GDP deflator through empirical analysis. The empirical analysis has been conducted by using the technique of Ordinary Least Square using annual data for the period from 1971-72 to 2006-07. Before applying OLS the stationarity of the data was checked by Augmented Dickey Fuller (ADF) test. Regression analysis proves that both cost-push and monetary factors are influenced on wholesale price index. The monetary variables have significant impact on GDP deflator.. There is no single remedy to control the raise of wholesale price index. Government should adopt multipurpose strategy such as improvement in tax and revenue structure, improving fiscal and monetary discipline, removing supply side disruptions, eradication of anti-competitive market practice.
    [Show full text]
  • Purchasing-Power Parity: Definition, Measurement, and Interpretation
    Purchasing-Power Parity: Definition, Measurement, and Interpretation Robert Lafrance and Lawrence Schembri, International Department • The concept of purchasing-power parity (PPP) has t has been argued that the Canadian dollar is two applications: it was originally developed as a undervalued because its current market value theory of exchange rate determination, but it is is below the purchasing-power-parity (PPP) I exchange rate calculated by the Organisation for now primarily used to compare living standards across countries. Economic Co-operation and Development (OECD) and Statistics Canada (Chart 1). While the deviation of • From the perspective of exchange rate determin- the value of the Canadian dollar from its purchasing- ation, PPP is useful as a reminder that monetary power-parity rate has been growing in recent years, policy has no long-run impact on the real exchange this article argues that this deviation cannot be inter- rate. Thus, countries with different inflation rates preted as implying that the Canadian dollar is under- should expect their bilateral exchange rate to adjust valued by a comparable amount. Instead, this deviation to offset these differentials in the long run. The indicates that the prices of goods and services are, on exchange rate, however, can deviate persistently average, lower in Canada than in the United States, from its PPP value in response to real shocks. when measured in the same currency at the prevailing exchange rate. • To compare living standards across countries, PPP exchange rates are constructed by comparing the national prices for a large basket of goods and Chart 1 services. These rates are used to translate different Canada’s PPP Exchange Rate currencies into a common currency to measure the purchasing power of per capita income in different US$/Can$ countries.
    [Show full text]