Movement Trajectory Mathematical Simulation of Backward Sliding Shot Put Under Mechanical Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2019 World Championships Statistics – Women’S PV by K Ken Nakamura
2019 World Championships Statistics – Women’s PV by K Ken Nakamura The records to look for in Doha: 1) Can Sandi Morris become only the second US PV to win the World Championships? 2) Can Eliza McCartney become the first PV from NZL to win a medal at World Championships? Summary: All time Performance List at the World Championships Performance Performer Height Name Nat Pos Venue Year 1 1 5.01WR Yelena Isinbayeva RUS 1 Helsinki 2005 2 2 4.91 Ekaterini Stefanidi GRE 1 London 2017 3 3 4.90 Yarisley Silva CUB 1 Beijing 2015 4 4.89 Yelena Isinbayeva 1 Moskva 2013 5 4 4.85 Fabiana Murer BRA 1 Daegu 2011 5 4.85 Fabiana Murer 2 Beijing 2015 7 5 4.82 Jennifer Suhr USA 2 Moskva 2013 7 4.82 Yarisley Silva 3 Moskva 2013 9 4.80 Yelena Isinbayeva 1 Osaka 2007 9 6 4.80 Martina Strutz GER 2 Daegu 2011 9 6 4.80 Nikoleta Kiriakapoulou GRE 3 Beijing 2015 Margin of Victory Difference Height Name Nat Venue Year Max 41cm 5.01m Yelena Isinbayeva RUS Helsinki 2005 Min 0cm 4.75m Stacy Dragila USA Edmonton 2001 Best Marks for Places in the World Championships Pos Height Name Nat Venue Year 1 5.01 Yelena Isinbayeva RUS Helsinki 2005 2 4.85 Fabiana Murer BRA Beijing 2015 4.82 Jennifer Suhr USA Moskva 2013 4.80 Martina Strutz GER Daegu 2011 4.75 Svetlana Feofanova RUS Edmonton 2001 Katerina Badurova CZE Osaka 2007 Sandi Morris USA London 2017 3 4.82 Yarisley Silva CUB Moskva 2013 4.75 Svetlana Feofanova RUS Osaka 2007 Svetlana Feofanova RUS Daegu 2011 4 4.75 Monika Pyrek POL Osaka 2007 Silke Spiegelburg GER Moskva 2013 Multiple Gold Medalists: Yelena Isinbayeva (RUS): -

THE WORKS of NAKAJIMA ATSUSHI "War Is War and Literature Is Literature"
THE WORKS OF NAKAJIMA ATSUSHI "War is war and literature is literature" A Thesis Presented in Partial FulfiUment of the Requirements for the degree of Master of Arts in the Graduate School of the Ohio State University by Scott Charles Langton '* '* ...... The Ohio State University 1992 Master's Examination Committee: Approved by James Morita /} Richard Torrance WiUiam Tyler ~L1~~ Advise;: Department of East Asian Languages & Literatures ACKNOWLEOOMENTS I am grateful to Dr. Richard Torrance for his kind guidance and support through the course of this research. Special thanks are also due to Drs. William Tyler and James Morita for their most helpful suggestions and comments. And to my wife, Lindsay, whose patience, help and encouragement buoyed me during this project, I offer my deepest thanks. u VITA October 21. 1962 Born - Orrville. Ohio 1984 B.A.. University of California. Los Angeles. California 1986-1988 Sales Representative. Mitsui Air- International Inc.. Los Angeles, California 1989-1990 Account Executive. Kintetsu World Express Inc., Cleveland, Ohio 1990-Present Graduate Teaching Assistant. Dept. of East Asian Language and Literature. Ohio State University. Columbus, Ohio FIELDS OF STUDY Major Field: East Asian Languages and Literatures • Japanese Literature • Japanese Linguistics TABLE OF CONTENTS ACKNOWLEI>GMENTS 11 VITA iii INTRODUCT ION 1 CHAPTER PAGE I. BACKGROUND AND PHILOSOPHy........................................... 9 II. LATE FICTION 49 III. "WAR IS WAR AND LITERATURE IS LITERATURE" 74 CHRONOL<XiY "............................................................................... 92 BIBLI()GRAPHY 95 lV INTRODUCTION The fiction for which Nakajima Atsushi (1909-1942) is best known was published in the early years of the Pacific War, a period coinciding with the end of his life. -

The Influence of Migration on the Burden of and Response to Infectious Disease Threats in China a Theoretically Informed Review
The Influence of Migration on the Burden of and Response to Infectious Disease Threats in China A Theoretically Informed Review Joseph D. Tucker, Chun Hao, Xia Zou, Guiye Lv, Megan McLaughlin, Xiaoming Li and Li Ling Migration and Health in China A joint project of United Nations Research Institute for Social Development Sun Yat-sen Center for Migrant Health Policy Working Paper 2013–3 November 2013 UNRISD Working Papers are posted online to stimulate discussion and critical comment. The United Nations Research Institute for Social Development (UNRISD) is an autonomous research institute within the UN system that undertakes multidisciplinary research and policy analysis on the social dimensions of contemporary development issues. Through our work we aim to ensure that social equity, inclusion and justice are central to development thinking, policy and practice. UNRISD, Palais des Nations, 1211 Geneva 10, Switzerland; Tel: +41 (0)22 9173020; Fax: +41 (0)22 9170650; [email protected]; www.unrisd.org The Sun Yat-sen Center for Migrant Health Policy (CMHP) is a multidisciplinary research institution at Sun Yat-sen University (SYSU), Guangzhou, China. Funded by the China Medical Board (CMB), CMHP was established by the School of Public Health, School of Business, School of Government, School of Sociology and Anthropology and Lingnan College of SYSU in 2009. CMHP aims to take a leading role and act as a hub for research, communication and policy advocacy on issues relating to health and migration in China. Sun Yat-sen Center for Migrant Health Policy, Sun Yat-sen University, #74, Zhongshan Road II, Guangzhou City 510080, P.R. -

Association Between Acculturation and Body Weight Status Among Migrant Children in Guangzhou, China: a Cross-Sectional Study Xiaoling Huang
Old Dominion University ODU Digital Commons Community & Environmental Health Faculty Community & Environmental Health Publications 2018 Association Between Acculturation and Body Weight Status Among Migrant Children in Guangzhou, China: A Cross-Sectional Study Xiaoling Huang Wen Chen Yanwei Lin Qi Zhang Old Dominion University, [email protected] Li Ling Follow this and additional works at: https://digitalcommons.odu.edu/commhealth_fac_pubs Part of the Community Health and Preventive Medicine Commons Repository Citation Huang, Xiaoling; Chen, Wen; Lin, Yanwei; Zhang, Qi; and Ling, Li, "Association Between Acculturation and Body Weight Status Among Migrant Children in Guangzhou, China: A Cross-Sectional Study" (2018). Community & Environmental Health Faculty Publications. 61. https://digitalcommons.odu.edu/commhealth_fac_pubs/61 Original Publication Citation Huang, X., Chen, W., Lin, Y., Zhang, Q., & Ling, L. (2018). Association between acculturation and body weight status among migrant children in Guangzhou, China: A cross-sectional study. BMJ Open, 8(6), e018768. doi:10.1136/bmjopen-2017-018768 This Article is brought to you for free and open access by the Community & Environmental Health at ODU Digital Commons. It has been accepted for inclusion in Community & Environmental Health Faculty Publications by an authorized administrator of ODU Digital Commons. For more information, please contact [email protected]. Open access Research Association between acculturation and body weight status among migrant children in Guangzhou, China: a cross- sectional study Xiaoling Huang,1,2 Wen Chen,1,2 Yanwei Lin,1,2 Qi Zhang,2,3 Li Ling1,2 To cite: Huang X, Chen W, Lin Y, ABSTRACT Strengths and limitations of this study et al. Association between Objective To assess the association between acculturation and body weight acculturation and body weight status among internal status among migrant children ► This study controlled mental health, dietary and pri- migrant children in China. -

Asian Games, Doha 2006
ASIAN GAMES Doha, Qatar 2006 100 METRES (8 Dec) HEAT 1 (+1.00m) 1 Yahya Saeed Al-Ghahes Saudi Arabia 10.42 2 Wachara Sondee Thailand 10.42 3 Naoki Tsukahara Japan 10.47 4 Lim Hee-nam South Korea 10.62 5 Khalid Yousuf Al-Obaidli Qatar 10.65 6 Aleksandr Zolotukhin Kyrghizstan 11.16 7 Masoud Azizi Afghanistan 11.40 HEAT 2 (+0.30m) 1 Abdullah Ibrahim Al-Waleed Qatar 10.46 2 Vyacheslav Muravyev Kazakhstan 10.53 3 Hu Kai China 10.64 4 Youssef Awlad Thani Oman 10.83 5 Jeon Duk-hyung South Korea 10.87 6 Lun Chhay Cambodia 11.42 7 Zahir Naseer Maldives 11.80 HEAT 3 (+0.50m) 1 Yahya Hassan Habeeb Saudi Arabia 10.49 2 Mohamed Sanad Al-Rashidi Bahrain 10.54 3 Liu Yuan-kai Taiwan 10.68 4 Umanga Surendra Sanjeewa Sri Lanka 10.80 5 Juma Mubarak Al-Jabri Oman 10.81 6 Leung Chun-wai Hong Kong 10.82 7 Ali Shareef Maldives 11.97 HEAT 4 (-0.10m) 1 Shigeyuki Kojima Japan 10.49 2 Sompote Suwannarangsri Thailand 10.49 3 Khalil Al-Hanahneh Jordan 10.66 4 Wen Yongyi China 10.68 5 Chiang Wai-hung Hong Kong 10.72 Saleh Hareth Iraq DNFin NON-PARTICIPANTS Faraj Salem Abdullah Bahrain Anil Prakash Kumar India Bharmappa Nagaraj India Denis Kondratyev Kazakhstan Hamoud Abdullah Al-Saad Kuwait Tsai Meng-lin Taiwan Jouma Bilal Al-Salfa United Arab Emirates Omar Juma Al-Salfa United Arab Emirates Asian Games, Doha 2006 - 1 - 100 METRES (9 Dec) SEMI-FINALS HEAT 1 (+0.80m) 1 Abdullah Ibrahim Al-Waleed Qatar 10.37 2 Naoki Tsukahara Japan 10.42 3 Yahya Hassan Habeeb Saudi Arabia 10.45 4 Vyacheslav Muravyev Kazakhstan 10.46 5 Sompote Suwannarangsri Thailand 10.52 6 Liu Yuan-kai -

The Sustainability Gap: a Case Study of Olympic Development
THE SUSTAINABILITY GAP: A CASE STUDY OF OLYMPIC DEVELOPMENT IN SYDNEY, AUSTRALIA AND BEIJING, CHINA by ANDREA BLASER A THESIS Presented to the Interdisciplinary Studies Program: Historic Preservation and the Graduate School ofthe University ofOregon in partial fulfillment ofthe requirements for the degree of Master of Science September 2008 11 "The Sustainability Gap: A Case Study of Olympic Development in Sydney, Australia and Beijing, China," a thesis prepared by Andrea Blaser in partial fulfillment ofthe requirements for the Master ofScience degree in the Interdisciplinary Studies Program: Historic Preservation. This thesis has been approved and accepted by: Mark Gillem, Chair ofthe Examining Committee Date Committee in Charge: Mark Gillem, Chair Deborah Hurtt Liz Carter Accepted by: Dean ofthe Graduate School 111 © 2008 Andrea Blaser iv An Abstract ofthe Thesis of Andrea Blaser for the degree of Master of Science in the Interdisciplinary Studies Program: Historic Preservation to be taken September 2008 Title: THE SUSTAINABILITY GAP: A CASE STUDY OF OLYMPIC DEVELOPMENT IN SYDNEY, AUSTRALIA AND BEIJING, CHINA Approved: _ Mark Gillem A media uproar occurred in 2006 after a wrecking ball flattened an Imperial-era hutong neighborhood in Beijing. While this kind ofnews story would often be ignored as just another example ofthe Chinese government destroying cultural history in the name ofprogress, the story of Qianmen had a new twist. Not only was Qianmen a protected heritage area under a 2002 Beijing Municipal Government Conservation Plan, but the destruction was said to have happened because ofthe upcoming 2008 Summer Olympic Games. Was the development ofQianmen in step with Olympic ideals and sustainable development? This thesis explores the sustainable development agenda ofthe International Olympic Committee, Agenda 21, in order to analyze the agenda, its impact in driving development policies in host cities Sydney, Australia and Beijing, China, and to what v extent planners incorporated historic preservation into Olympic development policies in both cities. -

Jan. 22, 2011 Qiulin Chen 陈秋霖
Jan. 22, 2011 Qiulin Chen 陈秋霖 Walter H. Shorenstein Asia-Pacific Research Center, Stanford University 616 Serra St., Encina Hall E335, Stanford, CA 94305-6055, USA (650) 736-0771; Fax (650) 723-6530, [email protected] National School of Development, Peking University 5 Yi He Yuan Road, Haidian District, Beijing 100871, China 86-13683383473(C); [email protected] Education 09.2004-07.2010 National School of Development, PEKING UNIVERSITY Ph.D. in Economics Dissertation Topic: The Effects of Health Care System on Health Performance (Advisor: Prof. Ling Li; Advisory Committee: Prof. Justin Yifu Lin, Prof. Ping Chen) 09.2001-07.2004 China Center for Economic Research, PEKING UNIVERSITY M.A. Candidate in Economics (Advisor: Prof. Dayuan Hu) 09.1997-07.2001 School of Business, NANJING UNIVERSITY B.A. in Business Administration (Advisor: Prof. Zhiming Cheng) Work Experience 01.2011- Walter H. Shorenstein Asia-Pacific Research Center, Stanford University Postdoctoral Fellow in Comparative Health Policy 07.2010- National School of Development, Peking University Postdoctoral Fellow 03.2004-06.2008 China Center for Economic Research (CCER), Peking University Executive Assistant to the Director (Prof. Justin Yifu Lin; Prof. Ling Li) 08.2003-01.2004 Merck Sharp & Dohme (China) Ltd. Beijing Office Research Assistant, Corporate Affairs Department (Internship) Teaching and Research Experience 09.2001-02.2007 CCER / Beijing International MBA Program (BiMBA), Peking University Teaching Assistant (Part-time) z Undergraduate: Health Economics, Information -

Entry List by NOC NOC別エントリーリスト / Liste D'inscriptions Par CNO As of MON 26 JUL 2021
Athletics 陸上競技 / Athlétisme Entry List by NOC NOC別エントリーリスト / Liste d'inscriptions par CNO As of MON 26 JUL 2021 Men Athlete Height Season Personal World NOC Name Date of Birth Event Bib m / ft in Best Best Ranking AFG - Afghanistan 1002 NOOR ZAHI Sha Mahmood 21 MAR 1991 - / - 100m - Total Athletes: 1 ALB - Albania 1004 SMAJLAJ Izmir 29 MAR 1993 - / - Long Jump 7.91 8.11 63 Total Athletes: 1 ALG - Algeria 1006 BOUCHICHA Hichem 19 MAY 1989 - / - 3000m Steeplechase 8:15.88 8:15.88 58 1007 HETHAT Yassine 30 AUG 1991 - / - 800m 1:44.25 1:44.25 69 1008 LAHOULOU Abdelmalik 7 MAY 1992 - / - 400m Hurdles 49.45 48.39 13 1009 MAKHLOUFI Taoufik 29 APR 1988 - / - 1500m 3:28.75 15 1010 SEDJATI Djamel 3 MAY 1999 - / - 800m 1:44.91 1:44.91 91 1011 TABTI Bilal 7 JUN 1993 - / - 3000m Steeplechase 8:47.50 8:20.20 85 1012 TRIKI Yasser Mohamed 24 MAR 1997 - / - Triple Jump 17.33 17.33 9 Total Athletes: 7 AND - Andorra 1021 MOYA Pol 9 DEC 1996 - / - 800m 1:48.97 1:46.96 209 Total Athletes: 1 ANG - Angola 1022 MIGUEL Aveni 19 AUG 2002 - / - 100m - Total Athletes: 1 ANT - Antigua and Barbuda 1024 GREENE Cejhae 6 OCT 1995 - / - 100m 10.00 10.00 30 Total Athletes: 1 ARG - Argentina 1027 ARBE Joaquin 25 AUG 1990 - / - Marathon 2:11:02 318 1028 CHIARAVIGLIO German 16 APR 1987 - / - Pole Vault 5.61 5.75 25 1029 MUNOZ Eulalio 16 JUL 1995 - / - Marathon 2:09:59 241 Total Athletes: 3 ARM - Armenia 1038 AGHASYAN Levon 19 JAN 1995 - / - Triple Jump 17.16 17.16 36 Total Athletes: 1 ATH-------------------------------_32A 1 Report Created MON 26 JUL 2021 17:28 Page 1/77 -

2010 Newsletter
Department of Asian Studies Spring 2011 Letter from the Chair... Dear Friends and Alumni, made it possible for us to offer made progress in drafting plans courses in Turkish language and for our future graduate programs Greetings from New West where culture, a position ably filled by in Asian Studies. On top of these spring leaves are sprouting on the Dr. Canguzel Zufilkar. The Col- duties, Li-ling coordinated the Inside this issue: trees and daffodils are blooming! lege of Arts and Sciences sup- programs in Arabic and Hebrew, I am pleased to report to you on ported growth in the Department developed a Chinese summer our growing programs, new fac- of Asian Studies in many ways, immersion program, published ulty, and diverse activities. We too, allowing us to hire as full- several articles, and still found Chair’s Column 1 expanded our newsletter this time instructors Ms. Farida Badr time to practice the Chinese musi- academic year to cover all the in Arabic, Ms. Jia Lin in Chinese, cal instrument known as the guz- good news. and Dr. Shahla Adel in Persian. heng. We wish Li-ling Hsiao well Faculty News 2 Dr. Morgan Pitelka joined the as she embarks on her well- The colorful images that you see Department as Associate Profes- deserved research leave. Lecturer Highlights 4 in this newsletter give a taste of sor of Japanese Studies. All our the year’s events. These represent new instructors have brought One of our major activities was to just a few of the activities of all dedication and energy to their host the 50th anniversary meeting Giveret Retires 5 kinds that faculty initiate to attract posts. -
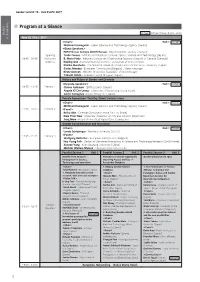
Program at a Glance Program at a Glance
Gender Summit 10 – Asia Pacific 2017 Program at a Glance Program at a Glance 同時通訳 Interpretation (ENG - JPN) May 25 (Thu.), 2017 <Chair> Hall 1 同時通訳 Michinari Hamaguchi - Japan Science and Technology Agency [Japan] <Guest Speakers> HRH Princess Sumaya bint El Hassan - Royal Scientific Society [Jordan] Opening Taido Tanose - Ministry of Education, Culture, Sports, Science and Technology [Japan] 08:45 - 09:45 Welcome B. Mario Pinto - Natural Sciences and Engineering Research Council of Canada [Canada] Address Ruiping Gao - National Natural Science Foundation of China [China] Kimiko Murofushi - The National University Corporation Ochanomizu University [Japan] Carlos Moedas - European Commission [Belgium] : Video message Kirsty Duncan - Minister of Science [Canada] : Video message Takashi Onishi - Science Council of Japan [Japan] History and Future of Gender and Diversity <Keynote Speakers> Hall 1 同時通訳 09:55 - 11:15 Plenary 1 Chieko Asakawa - IBM Research [Japan] Angela Ki Che Leung - University of Hong Kong [Hong Kong] Juichi Yamagiwa - Kyoto University [Japan] Female Researchers Tackling Global Serious Issues <Chair> Hall 1 同時通訳 Michinari Hamaguchi - Japan Science and Technology Agency [Japan] 11:30 - 12:45 Plenary 2 <Panel> Reiko Abe - Oriental Consultants India Pvt. Ltd. [India] Daw Than Nwe - Myanmar Academy of Arts and Science [Myanmar] Seng Mom - Royal University of Agriculture [Cambodia] Gender-based Research and Innovation <Chair> Hall 1 同時通訳 Londa Schiebinger - Stanford University [U.S.A.] 13:45 - 15:15 Plenary 3 <Panel> Wolfgang Burtscher - European Commission [Belgium] Hee Young Paik - Center for Gendered Innovations in Science and Technology Research [South Korea] Xueyan Yang - Xi'an Jiaotong University [China] Mathias Wullum Nielsen - Stanford University [U.S.A.] Parallel Session 1 Hall 1 Parallel Session 2 Hall 2 Parallel Session 3 Hall 3 Benefits from Women's Promotion of Gender Equality by Gender Dimensions in Sport Participation in Science, Improving Access and Use of Technology and Innovation Researcher Database <Chair> 1. -

Giovanni Polazzi
GIOVANNI POLAZZI After graduating in architecture with top marks from the University of Florence, Polazzi obtained his PhD in architectural and urban planning at the same University with a dissertation titled “Raffaello Fagnoni Florentine Architect – Analysis of a career divided between teaching and professional activities”. In 1988 he founded the Archea firm, conducting planning and research in the fields of architecture, town planning and industrial design. Didactic activities In the course of the years Polazzi has been professor under contract at the architecture faculty of the University of Genoa where he has taught interior architecture, and at the architecture faculty of Parma where he has taught architectural planning. At present he holds a professorship at the architecture faculty of the University of Florence, heading ‘architecture planning workshop I’. His didactic activities are developed through a close relationship between theoretic lessons and development of design in the classroom, with the purpose of investigating the relationship between the compositive idea and the architectural theme. The courses aim to reach, together with the student, the definition of an architectural project in every part, representing it from the scale of the landscape to the details. Professional activity Together with his firm he has participated in very important national and international architecture competitions and consultations, obtaining numerous recognitions and prizes: from the first prize in the competition for the business and shopping -

Commencement Program 2012, University of Pennsylvania
256 th COMMENCEMENT 256th COMMENCEMENT MAY 14 2012 MAY 14 MAY 2012 UNIVERSITY OF PENNSYLVANIA KEEPING FRANKLIN’S PROMISE In the words of one elegiac tribute, “Great men have two lives: one which occurs while they work on this earth; a second which begins at the day of their death and continues as long as their ideas and conceptions remain powerful.” These words befit the great Benjamin Franklin, whose inventions, innovations, ideas, writings, and public works continue to shape our thinking and renew the Republic he helped to create and the institutions he founded, including the University of Pennsylvania. Nowhere does Franklin feel more contemporary, more revolutionary, and more alive than at the University of Pennsylvania. His startling vision of a secular, nonsectarian Academy that would foster an “Inclination join’d with an Ability to serve Mankind, one’s Country, Friends and Family” has never ceased to challenge Penn to redefine the scope and mission of the modern American university. When pursued vigorously and simultaneously, the two missions – developing the inclination to do good and the ability to do well – merge to help form a more perfect university that educates more capable citizens for our democracy. Penn has embodied and advanced Franklin’s revolutionary vision for 272 years. Throughout its history, Penn has extended the frontiers of higher learning and research to produce graduates and scholars whose work has enriched the nation and all of humanity. The modern liberal arts curriculum as we know it can trace its roots to Franklin’s innovation to have Penn students study international commerce and foreign languages.