DOCSLIB.ORG

PMATH 340 Lecture Notes on Elementary Number Theory

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
PMATH 340 Lecture Notes on Elementary Number Theory PMATH 340 Lecture Notes on Elementary Number Theory Anton Mosunov Department of Pure Mathematics University of Waterloo Winter, 2017 Contents 1 Introduction . .3 2 Divisibility. Factorization of Integers. The Fundamental Theorem of Arithmetic . .5 3 Greatest Common Divisor. Least Common Multiple. Bezout’s´ Lemma. .9 4 Diophantine Equations. The Linear Diophantine Equation ax + by = c ........... 15 5 Euclidean Algorithm. Extended Euclidean Algorithm . 18 6 Congruences. The Double-and-Add Algorithm . 24 7 The Ring of Residue Classes Zn .................. 29 8 Linear Congruences . 31 ? 9 The Group of Units Zn ....................... 33 10 Euler’s Theorem and Fermat’s Little Theorem . 36 11 The Chinese Remainder Theorem . 38 12 Polynomial Congruences . 41 13 The Discrete Logarithm Problem. ? The Order of Elements in Zn .................... 45 14 The Primitive Root Theorem . 50 15 Big-O Notation . 53 16 Primality Testing . 56 16.1 Trial Division . 57 16.2 Fermat’s Primality Test . 58 16.3 Miller-Rabin Primality Test . 61 17 Public Key Cryptosystems. The RSA Cryptosystem . 62 18 The Diffie-Hellman Key Exchange Protocol . 67 19 Integer Factorization . 69 1 19.1 Fermat’s Factorization Method . 70 19.2 Dixon’s Factorization Method . 72 20 Quadratic Residues . 75 21 The Law of Quadratic Reciprocity . 81 22 Multiplicative Functions . 86 23 The Mobius¨ Inversion . 91 24 The Prime Number Theorem . 95 25 The Density of Squarefree Numbers . 96 26 Perfect Numbers . 101 27 Pythagorean Triples . 104 28 Fermat’s Infinite Descent. Fermat’s Last Theorem . 105 29 Gaussian Integers . 110 30 Fermat’s Theorem on Sums of Two Squares . 120 31 Continued Fractions . 124 32 The Pell’s Equation . 135 33 Algebraic and Transcendental Numbers. Liouville’s Approximation Theorem . 137 34 Elliptic Curves . 140 2 1 Introduction This is a course on number theory, undoubtedly the oldest mathematical discipline known to the world. Number theory studies the properties of numbers. These may be integers, likep −2;0 or 7, or rational numbers like 1=3 or −7=9, or algebraic numbers like 2 or i, or transcendental numbers like e or p. Though most of the course will be dedicated to Elementary Number Theory, which studies con- gruences and various divisibility properties of the integers, we will also dedicate several lectures to Analytic Number Theory, Algebraic Number Theory, and other subareas of number theory. There are many interesting questions that one might ask about numbers. In search for answers to these questions mathematicians unravel fascinating proper- ties of numbers, some of which are quite profound. Here are several curious facts about prime numbers: 1. Every odd number exceeding 5 can be expressed as a sum of three primes (Helfgott-Vinogardov Theorem, 2013. In 1954, Vinogardov proved the re- sult for all odd n > B for some B, and in 2013 Helfgott demonstrated that one can take B = 5); 2. There are infinitely many prime numbers p and q such that jp − qj ≤ 246 (Zhang’s Theorem, 2013. Zhang proved the result for 7 · 107, and in 2014 the constant was reduced to 246 by Maynard, Tao, Konyagin and Ford); 3. For all n ≥ exp(exp(33:217)) there always exists a prime between n3 and (n + 1)3 (Ingham’s Theorem, 1937. Ingham proved the result for all n ≥ B for some B, and in 2014 Dudek demonstrated that one can take B as above); 4. There are infinitely many primes of the form x2 + y4 (Friedlander-Iwaniec Theorem, 1997); 5. Up to x > 1, there are “approximately” x=logx prime numbers (Prime Num- ber Theorem, 1896); 6. Given a positive integer d, there exist distinct prime numbers p1; p2;:::; pd which form an arithmetic progression (Green-Tao Theorem, 2004). Despite the simplicity of their formulations, all of these results are highly non- trivial and their proofs reside on some deep theories. For example, the Green-Tao 3 Theorem resides on Szemeredi’s´ Theorem, which in turn uses the theory of ran- dom graphs. There are many number theoretical problems out there that are still open. At the 1912 International Congress of Mathematicians, the German mathematician Edmund Landau listed the following four basic problems about primes that still remain unresolved: 1. Can every even integer greater than 2 be written as a sum of two primes? (Goldbach’s Conjecture, 1742); 2. Are there infinitely many prime numbers p and q such that jp − qj = 2? (Twin Prime Conjecture, 1849); 3. Does there always exist a prime between two consecutive perfect squares? (Legendre’s Conjecture, circa 1800); 4. Are there infinitely many primes of the form n2 + 1? (see Bunyakovsky’s Conjecture, 1857). It is widely believed that the answer to each of the questions above is “yes”. There is a lot of computational evidence towards each of them, and for some of them conjectural asymptotic formulas were established. However, none of them are proved. Aside from being an interesting theoretical subject, number theory also has many practical applications. It is widely used in cryptographic protocols, such as RSA (Rivest-Shamir-Adleman, 1977), the Diffie-Hellman protocol (1976), and ECIES (Elliptic Curve Integrated Encryption Scheme). These protocols rely on certain fundamental properties of finite fields (RSA, D-H) and elliptic curves de- fined over them (ECIES). For example, consider the Discrete Logarithm Problem: given a prime p and integers c;m, one may ask whether there exists an integer d such that cd − m is divisible by p, and if so, what is its value. We may write this in the form of a congruence cd ≡ m (mod p): When p is extremely large (hundreds of digits) and c;m are chosen properly, this problem is widely believed to be intractable; that is, no modern computer can solve it in a reasonable amount of time (the computation would require billions of 4 years). This property is used in many cryptosystems, including the first two men- tioned above. Many cryptosystems, like RSA, can be broken by quantum comput- ers. The construction of protocols infeasible to attacks by quantum computers is a subject of Post Quantum Cryptography and number theory plays a crucial role there (see the Lattice-Based or Isogeny-Based Cryptography). 2 Divisibility. Factorization of Integers. The Fundamental Theorem of Arithmetic Before we proceed, let us invoke a little bit of notation: N = f1;2;3;:::g — the natural numbers; Z = f0;±1;±2;:::g — the ring of integers; m Q = n : m 2 Z;n 2 N — the field of fractions; R — the field of real numbers; C = fa + bi: a;b 2 R;i2 = −1g — the field of complex numbers. We call Z a ring because 0;1 2 Z and a;b 2 Z implies a±b 2 Z and a · b 2 Z. In other words, Z is closed under addition, subtraction and multiplication. Note, however, that a;b 2 Z with b 6= 0 does not imply that a=b 2 Z, so it is not closed under division. A collection that is closed under addition, subtraction, multipli- cation and division by a non-zero element is called a field. According to this definition, every field is also a ring. Exercise 2.1. Demonstrate the proper inclusions in N(Z(Q(R(C. No proofs are required. Definition 2.2. Let a;b 2 Z. We say that a divides b, or that a is a factor of b, when b = ak for some k 2 Z. We write a j b if this is the case, and a - b otherwise. Example 2.3. 3 j 12 because 12 = 3 · 4; 3 - 13; −1 j 7 because 7 = (−1) · (−7); 0 - 3. Proposition 2.4. 1 Let a;b;c;x;y 2 Z. 1. If a j b and b j c, then a j c; 1Proposition 1.2 in Frank Zorzitto, A Taste of Number Theory. 5 2. If c j a and c j b, then c j ax ± by; 3. If c j a and c - b, then c - a ± b; 4. If a j b and b 6= 0, then jaj ≤ jbj; 5. If a j b and b j a, then a = ±b; 6. If a j b, then ±a j ±b; 7. 1 j a for all a 2 Z; 8.a j 0 for all a 2 Z; 9. 0 j a if and only if a = 0. Proof. Exercise. Definition 2.5. Let p ≥ 2 be a natural number. Then p is called prime if the only positive integers that divide p are 1 and p itself. It is called composite otherwise. We remark that 1 is neither prime nor composite. We will also use the above terminology only with respect to integers exceeding 1 (so according to this con- vention −3 is not prime and −6 is not composite). Exercise 2.6. Among the collection −5;1;5;6, which numbers are prime? Theorem 2.7. For each integer n ≥ 2 there exists a prime p such that p j n. Proof. We will prove this result using strong induction on n. Base case. For n = 2 we have 2 j n. Since 2 is prime, the theorem holds. Induction hypothesis. Suppose that the theorem is true for n = 2;3;:::;k. Induction step. We will show that the theorem is true for n = k + 1. If n is prime the result holds. Otherwise there exists a positive integer d such that d j n, d 6= 1 and d 6= n. By property 4 of Proposition 2.4 we have d ≤ n, and since d 6= 1 and d 6= n we conclude that 2 ≤ d ≤ n − 1 = k.
Load more

Recommended publications
  • Divisibility Rules Workbook
    Name _____________________ Divisibility A number is divisible by another number if it is a true multiple of the other number (or if the division problem does not have a remainder. 24 is divisible by 3 because 24 ÷ 3 = 8 with no remainder. 25 is not divisible by 3 because it would have a remainder of 1! This first section of this booklet will help you to learn the divisibility rules that you will need and use every day. The numbers are all less than 169 because using the Fraction Actions method, you will never end up with numbers greater than 169 that are not already finished numbers. The last section of the book will help you with a few rules that you will need to know for NC EOG testing purposes. Divisibility Rules Divisibility Rule for 2 When the last digit in a number is 0, 2, 4, 6, or 8, the number is divisible by 2 Divisibility Rule for 5 When the last digit in a number is 0 or 5, the number is divisible by 5 Divisibility Rule for 3 When the sum of the digits is a multiple of 3, the number is divisible by 3 Divisibility Rule for 7 Double the last digit in a number and subtract it from the rest of the number. If the result is a known multiple of 7, then the number is divisible by 7. If the result is not known, repeat the rule with the new number! Divisibility Rule for 11 When the sum of the odd digits is equal to (or 11 more than) the sum of the even digits, the number is divisible by 11 Divisibility Rule for 13 Nine times the last digit in a number and subtract it from the rest of the number.
    [Show full text]
  • Divisibility Rules Pathway 1 OPEN-ENDED
    Divisibility Rules Pathway 1 OPEN-ENDED You will need I wonder if 72 is divisible by 9. • base ten blocks (optional) • a calculator Rememberemember • If a number is We know that 72 is divisible by 2, 3, 6, and 9 because you can divisible by another make groups of 2, 3, 6, or 9 and have nothing left over. number, when you divide them the For example, if you model 72 with blocks, you can make answer is a whole 8 groups of 9 and there are none left over. number. e.g., 72 4 6 5 12, so 72 is divisible by 6 (and by 12). 72 is divisible by 9 We know that 72 is not divisible by 5 or 10. This is because if you make groups of 5 or 10, there would always be some left over. A long time ago, people discovered shortcut rules for deciding whether numbers are divisible by 2, 3, 5, 6, 9, and 10. Each rule is one of these types: – If the ones digit of a number is ▲, the number is divisible by ❚. – If the sum of the digits of a number is divisible by ▲, the number is divisible by ❚. – If a number is divisible by both ▲ and ●, then it is also divisible by ❚. Note: Depending on the rule, the grey shape could represent 1 or more digits or a word. For example: – If the ones digit of a number is ▲, the number is divisible by ❚. If the ones digit of a number is even, the number is divisible by 2.
    [Show full text]
  • Divisibility Rules and Their Explanations
    Divisibility Rules and Their Explanations Increase Your Number Sense These divisibility rules apply to determining the divisibility of a positive integer (1, 2, 3, …) by another positive integer or 0 (although the divisibility rule for 0 says not to do it!)1. Explanations of the divisibility rules are included because understanding why a rule works helps you (1) to remember it and to use it correctly and (2) much more importantly, to deepen your knowledge of how numbers work. Some divisors have several divisibility rules; to limit the scope of this document, in most cases, only one divisibility rule is given for a divisor. A summary of the divisibility rules is included at the end. The explanations for these divisibility rules are divided into the following categories: x x x Last Digits 2 5 10 Modular Arithmetic 3 9 11 Composite Number Composites Prime Number Primes Other 0 1 00 11 22 33 44 55 66 77 88 99 1100 1111 1122 CCoommppoossiiitteess PPrriimmeess Before we get to the divisibility rules, let’s establish some groundwork required for the Last Digits and Modular Arithmetic explanations: Foundations: 1. Any integer can be rewritten as the sum of its ones + its tens + its hundreds + …and so on (for simplicity, we will refer to an integer’s ones, tens, hundreds, etc. as its “parts”). For example, the integer 3784 can be rewritten as the sum of its parts: 3000 + 700 + 80 + 4. 2. Dividing each of an integer’s parts by a divisor and summing the results gives the same result as dividing the integer as a whole by the divisor.
    [Show full text]
  • Week 4 of Virtual Guru Math Suhruth Vuppala Let’S Review What We Learned Last Time What Is the Area of Something?
    Welcome to Week 4 of Virtual Guru Math Suhruth Vuppala Let’s Review What We Learned Last Time What is the area of something? ● The area of a shape is how much space the shape takes up What is the perimeter of something? ● The perimeter of a shape is the length of the whole outside line or border of the shape ● The perimeter can usually be found by adding up all the side lengths of a shape How do you find the area of a square ● To find the area of the square you take one of the side lengths and multiply it by itself ● Let’s take the example of the square from two slides before. It has a side length of 5 centimeters, so you do 5x5 and you get the area ● What is the area of the square? How do you find the area of a rectangle? ● To find the area of a rectangle, you take the length of the top/bottom segments and multiply it by the length of the left/right segments ● Let’s use the example below. It has a right side length of 3 centimeters and a bottom side length of 8 centimeters. That means the area is 3x8 centimeters ● What is the area? How do you find the perimeter of a square? ● To find the perimeter of a square, you have to take one of the side lengths and multiply it by 4 ● Let’s again use the example from two slides before. It has a side length of 5 centimeters, so 5x4 is the perimeter of the square ● What is the perimeter? How do you find the perimeter of a rectangle? ● The perimeter of a rectangle can be found by doing 2 times the sum of the left/right and top/bottom ● In the example below, the right side length is 3 centimeters and the bottom side length is 8 centimeters.
    [Show full text]
  • Divisibility Rules © Owl Test Prep 2015
    Divisibility Rules © Owl Test Prep 2015 It’s my sincere hope that one of your elementary school teachers taught you these rules. If not, we can fix that. The rules can be broken down into 5 groups: 2, 4, and 8: Powers of 2 3 and 9: Multiples of 3 5 and 10: Multiples of 5 6: The mother of all divisibility rules However we can use the rules below to construct rules for lots of composite numbers. I’ll point out a couple of examples as we go along. Divisibility Rules for 2, 4, and 8 1) A number is divisible by 2 if a) The last digit is divisible by 2. For example 2,106 is divisible by two because the last digit, 6, is divisible by 2, but 2,119 is not divisible by 2 because 9 is not divisible by two. 2) A number is divisible by 4 if a) The last two digits form a number that is divisible by 4. For example 3,436 is divisible by 4 because 36 is divisible by 4, but 3,774 is not divisible by 4 because 74 is not divisibly by 4. Note that if the digit in the ten’s place is a zero the rule still applies; 104 and 2,308 are both divisible by 4. b) It is divisible by 2 twice. For example, , and 4, so 256 is divisible by 4, but 170 is not divisible by 4 because 170 , and 85 is not divisible by 2. Thus, 170 is only divisible by 2 once, so it is not divisible by 4.
    [Show full text]
  • Divisiblity Rules F (Taught).Notebook 1 August 07, 2013
    Divisiblity Rules F (taught).notebook August 07, 2013 Bell Ringer Name the decimal place indicated. Then round to that decimal place. Divisibility Rules 1. 67,149 2. 1.3446 3. 25.8 You will be able to . Divisiblity A number is divisible by another if the remainder • Determine whether a number is divisible by 2, is 0 when you divide. (In other words, if you get a 3, 5, 6, 9, or 10. whole number, not a decimal.) Ex: Divisible or not? a. 34 by 2 b. 10 by 4 c. 737 by 5 Divisibility Rule for 2 Example: Determine whether the following A number is divisible by 2 if it ends in 0, 2, 4, 6, numbers are divisible by 2. or 8. a. 542 b. 647 c. 9,001 d. 46 1 Divisiblity Rules F (taught).notebook August 07, 2013 Divisibility Rule for 5 Example: Determine whether the following A number is divisible by 5 if it ends in 0 or 5. numbers are divisible by 5. a. 75 b. 439 c. 3,050 d. 5 Divisibility Rule for 10 Example: Determine whether the following A number is divisible by 10 if it ends in 0. numbers are divisible by 10. a. 3005 b. 250 c. 622 d. 89,620 Example: State whether each number is divisible Your Turn: State whether each number is by 2, 5, or 10. (More than one answer is divisible by 2, 5, or 10. (More than one answer is possible!) possible!) a. 288 b. 300 c. 4,805 1. 50 2. 1,015 3.
    [Show full text]
  • Stupid Divisibility Tricks 101 Ways to Stupefy Your Friends Appeared in Math Horizons November, 2006
    Stupid Divisibility Tricks 101 Ways to Stupefy Your Friends Appeared in Math Horizons November, 2006 Marc Renault Shippensburg University Mathematics Department 1871 Old Main Road Shippensburg, PA 17013 [email protected] http://webspace.ship.edu/msrenault/divisibility/ 1 Introduction When is the last time this happened to you? You are stranded on a deserted island without a calculator and for some reason you must determine if 67 is a divisor of 95733553; furthermore, a coconut recently fell on your head and you have completely forgotten how to perform long division. Of course the above scenario would never happen (we all carry around calculators) but it's good to know that if we should ¯nd ourselves in a similar situation there is an easy divisibility rule for 67: remove the two rightmost digits from the number (in our case, 53), double them (106) and subtract that from the remaining digits (957335¡106 = 957229); the original number is divisible by 67 if and only if the resulting number is divisible by 67. If the resulting number is not obviously divisible by 67 we can repeat the process until we get a number that clearly is or is not a multiple of 67. In the above example, we get the following. 1 9573355==3 { 106 95722==9 { 58 951==4 { 28 67 Thus we conclude that in fact 95733553 is a multiple of 67. This article has two aims. First, to identify six categories of tests that most divisibility tricks fall into, and second, to provide an easy divisibility test for each number from 2 { 102 (thus the \101 Ways..." in the title).
    [Show full text]
  • Number Theory
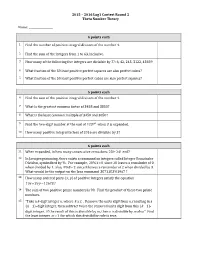
    2015 – 2016 Log1 Contest Round 2 Theta Number Theory Name: __________________ 4 points each 1 Find the number of positive integral divisors of the number 4. 2 Find the sum of the integers from 1 to 63, inclusive. 3 How many of the following five integers are divisible by 7?: 6, 42, 245, 3122, 43659 4 What fraction of the 50 least positive perfect squares are also perfect cubes? 5 What fraction of the 50 least positive perfect cubes are also perfect squares? 5 points each 6 Find the sum of the positive integral divisors of the number 4. 7 What is the greatest common factor of 3458 and 3850? 8 What is the least common multiple of 3458 and 3850? 9 Find the two-digit number at the end of 12373 when it is expanded. 10 How many positive integral factors of 2016 are divisible by 3? 6 points each 11 When expanded, in how many consecutive zeros does 23! 24! end? 12 In Java programming, there exists a command on integers called Integer Remainder Division, symbolized by %. For example, 20%1 0 since 20 leaves a remainder of 0 when divided by 1; also, 8%3 2 since 8 leaves a remainder of 2 when divided by 3. What would be the output on the Java command 3871183%1967 ? 13 How many ordered pairs xy, of positive integers satisfy the equation 19xy 29 12673? 14 The sum of two positive prime numbers is 99. Find the product of these two prime numbers. 15 “Take a k-digit integer n, where k 2 .
    [Show full text]
  • Divisibility Rules
    Divisibility Rules A number is divisible by another number if it divides evenly without a remainder. For example, 8 is divisible by 4 since 8 + 4 = 2 RO . The following divisibility rules apply to whole numbers. Divisor: 2 Divisibility Rule: Any whole number that ends in 0, 2, 4, 6, or 8 is divisible by 2. (i.e. Any even number is divisible by 2). Example: 78558 is divisible by 2 since the last digit is 8. Non-Example: 78559 is not divisible by since the last digit is 9. Divisor: 3 Divisibility Rule: If the sum of the digits is divisible by 3, then the whole number is also divisible by 3. Example: 1539 is divisible by 3 since 1 + 5 + 3 + 9 18 and 18 is divisible by 3. = Non-Example: 1540 is not divisible by 3 since 1 + 5 + 4 + 0 = 10 and 10 is not divisible by 3. ©Tutoring and Learning Centre, George Brown College, 2020 | www.georgebrown.ca/tlc Divisor: 4 Divisibility Rule: If the last two digits of the whole number form a two-digit number that is divisible by 4, then the whole number is also divisible by 4. Example: 19236 is divisible by 4 since the last two digits, 36, form a number that is divisible by 4. Non-Example: 19237 is not divisible by 4 since the last two digits, 37, form a number that is not divisible by 4. Divisor: 5 Divisibility Rule: Any whole number that ends in 0 or 5 is divisible by 5. Example: 87235 is divisible by 5 since the number ends in 5.
    [Show full text]
  • 6Thth Grade Math
    MATH TODAY Grade 6, Module 2, Topic D 2014/2015 th 6th Grade Math Focus Area Topic D: Module 2: Arithmetic Operations Including Divisibility Rules Division of Fractions Students use these rules to make determining if a larger Math Parent Letter number is divisible by 2, 3, 4, 5, 8, 9, or 10 easier. Divisibility Rule for 2: If and only if its last digit is even. This document is created to give parents and students a better understanding of the math concepts found in Engage New Divisibility Rule for 3: If the sum of the digits is divisible by York, which correlates with the California Common Core 3, then the number is divisible by 3. Standards. Module 2 of Engage New York introduces the concepts of Arithmetic Operations Including Division of Divisibility Rule for 4: If and only if its last two digits are a Fractions. number divisible by 4. Divisibility Rule for 5: If and only if its last digit is 0 or 5. Divisibility Rule for 8: If and only if the last three digits are a number divisible by 8. Divisibility Rule for 9: If the sum of the digits is divisible by Focus Area Topic D: 9, then the number is divisible by 9. Divisibility Rule for 10: If and only if its last digit is 0. Words to Know: Factor: 2 x 3 = 6 Focus Area Topic D: Factor Factor Greatest Common Factor Example Problems and Answers Multiples: Multiples of 6: 6, 12, 18, 24, 30… GCF 30 and 50 Multiples of 7: 7, 14, 21, 28, 32… Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30 Factors of 50: 1, 2, 5, 10, 25, Greatest Common Factor (GCF): The greatest of 50 the common factors of two or more numbers.
    [Show full text]
  • Divisibility Rules!
    Divisibility Rules! Investigating Divisibility Rules Learning Goals Key Term In this lesson, you will: divisibility rules Formulate divisibility rules based on patterns seen in factors. Use factors to help you develop divisibility rules. Understanding relationships between numbers can save you time when making calculations. Previously, you worked with factors and multiples of various numbers, and you determined which numbers are prime and composite by using the Sieve of Eratosthenes. By doing so, you determined what natural numbers are divisible by other natural numbers. In this lesson, you will consider patterns for numbers that are divisible by 2, 3, 4, 5, 6, 9, and 10. What type of patterns do you think exist between these numbers? Why do you think 1 is not a part of this list? © 2011 Carnegie Learning 1.4 Investigating Divisibility Rules • 35 © 2011 Carnegie Learning 1.4 Investigating Divisibility Rules • 35 Problem 1 Students explore the divisibility of numbers by 2, 5 and 10. Problem 1 Exploring Two, Five, and Ten They will list multiples of given numbers and notice 1. List 10 multiples for each number. all multiples of 2 are even numbers, all multiples of 5 have Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 a last digit that ends in a 0 or Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50 5, and all multiples of 10 are also multiples of both 2 and 5. Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 Students will write divisibility 2.
    [Show full text]
  • Divisibility Rules Justified Grades 6-8
    Divisibility Rules Justified Grades 6-8 Standards: 7 MR3.3 Develop generalizations of the results obtained and the strategies used and apply them to new problem situations. 7.EE.1 Use properties of operations to generate equivalent expressions. Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients. Materials: Class set of properties cards (pages 7-11) for students to use in pairs (or small groups) Partial notes handout (pages 12-13), one per student Introduction: “Divisibility rules can be quick shortcuts for factoring multi-digit numbers. Today we are going to examine why they work using proofs with variables. In middle school, you are not expected to be able to write proofs like this, but you will be able to justify each step, working with your partner (or small group).” Ex 1 (I Do): Divisibility rule for 3 A number is divisible by 3 iff (if and only if) the sum of its digits is a multiple of 3. The thousands digit times 1000, the Proof: hundreds digit times 100, the tens digit N N abcd Let be a four digit number such that = . times 10 plus the ones digit. N = a • 1000 + b •100 + c •10 + d Expanded notation N = a(999 +1) + b(99 +1) + c (9 +1) + d Decomposition N = 999 a + a + 99b + b + 9c + c + d Distributive Property of Multiplication Over Addition N = 999 a + 99 b + 9c + a + b + c + d Commutative Property of Addition N = 3• 333a + 3• 33b + 3• 3c + (a + b + c + d ) Decomposition In this step, we decompose into factors to show parts that are divisible by 3.
    [Show full text]