DOCSLIB.ORG

Landscape Development in the Western Transverse Ranges, California: Insights from Mapping, Geochronology, and Modeling

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Landscape Development in the Western Transverse Ranges, California: Insights from Mapping, Geochronology, and Modeling Landscape Development in the Western Transverse Ranges, California: Insights from Mapping, Geochronology, and Modeling Item Type text; Electronic Dissertation Authors DeLong, Stephen Publisher The University of Arizona. Rights Copyright © is held by the author. Digital access to this material is made possible by the University Libraries, University of Arizona. Further transmission, reproduction or presentation (such as public display or performance) of protected items is prohibited except with permission of the author. Download date 29/09/2021 06:14:07 Link to Item http://hdl.handle.net/10150/195640 LANDSCAPE DEVELOPMENT IN THE WESTERN TRANSVERSE RANGES, CALIFORNIA: INSIGHTS FROM MAPPING, GEOCHRONOLOGY, AND MODELING by Stephen Berend DeLong ______________________ A Dissertation Submitted to the Faculty of the DEPARTMENT OF GEOSCIENCES In Partial Fulfillment of the Requirements For the Degree of DOCTOR OF PHILOSOPHY In the Graduate College THE UNIVERSITY OF ARIZONA 2006 THE UNIVERSITY OF ARIZONA GRADUATE COLLEGE As members of the Dissertation Committee, we certify that we have read the dissertation prepared by Stephen B DeLong entitled “Landscape Development in the Western Transverse Ranges, California: Insights from Mapping, Geochronology, and Modeling” and recommend that it be accepted as fulfilling the dissertation requirement for the Degree of Doctor of Philosophy _______________________________________________________________________ Date: 4/03/06 Jon D Pelletier _______________________________________________________________________ Date: 4/03/06 Jay Quade _______________________________________________________________________ Date: 4/03/06 Clem Chase _______________________________________________________________________ Date: 4/03/06 Phil Pearthree Final approval and acceptance of this dissertation is contingent upon the candidate’s submission of the final copies of the dissertation to the Graduate College. I hereby certify that I have read this dissertation prepared under my direction and recommend that it be accepted as fulfilling the dissertation requirement. ________________________________________________ Date: 4/03/06 Dissertation Director: Jon D Pelletier STATEMENT BY AUTHOR This dissertation has been submitted in partial fulfillment of requirements for an advanced degree at the University of Arizona and is deposited in the University Library to be made available to borrowers under rules of the Library. Brief quotations from this dissertation are allowable without special permission, provided that accurate acknowledgement of source is made. Requests for permission for extended quotation from or reproduction of this manuscript in whole or in part may be granted by the head of the major department or the Dean of the Graduate College when in his or her judgment the proposed use of the material is in the interests of scholarship. In all other instances, however; permission must be obtained from the author. SIGNED: Stephen B DeLong TABLE OF CONTENTS ABSTRACT……………………………………………………………..………….5 INTRODUCTION……………………………………………………………….…7 PRESENT STUDY……………………………………………………….……….13 REFERENCES………………………………………………………………….…17 APPENDIX A: DATING ALLUVIAL DEPOSITS WITH OPTICALLLY STIMULATED LUMINESCENCE, AMS 14C AND COSMOGENIC TECHNIQUES, WESTERN TRANSVERSE RANGES, CALIFORNIA, USA………………………………………………………………………….…….20 APPENDIX B: COUPLED ALLUVIAL FAN AND AXIAL CHANNEL DEVELOPMENT IN CUYAMA VALLEY, CALIFORNIA…………………….50 APPENDIX C: GEOMORPHIC FATE OF LATE CENOZOIC BASINS IN SOUTHERN CALIFORNIA: AN EXAMPLE FROM THE UPPER CUYAMA VALLEY……………………………………………………….……..66 APPENDIX D: BEDROCK LANDSCAPE DEVELOPMENT MODELING: CALIBRATION USING FIELD STUDY, GEOCHRONOLOGY AND DEM ANALYSIS……………………………………………………………………..…96 5 ABSTRACT Understanding how climate and tectonics have interacted to shape current landscape configuration requires application of the latest geomorphological techniques. This dissertation presents results from a combination of field mapping, geochronology, and numerical landscape development modeling. The papers contained here focus on studies from Cuyama Valley, California, at the junction of the Coast Ranges and Western Transverse Ranges in southern California. Combining field observation with three geochronological techniques has led to a detailed understanding of the late Quaternary alluvial history of Cuyama Valley. The alluvial history, in turn, allows for a better understanding of important events in the history of landscape development. In the western Cuyama Valley, the timing and morphology of alluvial fans record both climatic forcing in the form of variable sediment supply from drainage basins, and tectonic forcing from ongoing tectonically driven incision of the axial Cuyama River. Fan-terrace surfaces are subparallel (older surfaces are slightly steeper) and offset systematically in relation to their ages, suggesting response to ongoing base-level incision and fluctuation in sediment supply. The fans aggraded during relatively cool and wet climate of the last glacial period, which is out-of- phase with the regional model developed in nearby desert regions. In the upper Cuyama Valley, deposition in the Cuyama sedimentary basin ceased in the mid-Pleistocene, after which basin fill was uplifted, deformed, and beveled, forming a low-relief erosion surface on which the alluvium of San Emigdio Mesa was 6 deposited. Subsequent fluvial drainage network development formed the Cuyama badlands by incising into the deformed Cuyama basin sediments. The history of the upper Cuyama Valley was used to calibrate a numerical landscape development model. Uplift rate U, bedrock erodibility K, and landslide threshold-slope Sc are related to steady-state relief, hypsometry, and drainage density for a wide range of synthetic topographies produced by a stream-power-based landscape development model. A combination of fluvial channels and threshold-slopes occurs for only a relatively narrow range of U/K between 10 and 5000 m·kyr/kyr. Using measured values for hypsometric integral, drainage density and relief, the U/K value can be further constrained, enabling K to be determined if U is known. 7 INTRODUCTION This dissertation addresses fundamental questions that relate climate and tectonics to landscape development. Though the dissertation is a compilation of manuscripts with coauthors, the research design and execution is largely that of the first author. Appendix A presents results of an intercomparison of geochronological techniques as applied to alluvial deposits. Accurate age-determination of alluvial deposits in arid and semi-arid climates is possible using a number of techniques; each with its own limitations. Most widely applied are radiocarbon dating, cosmogenic radionuclide surface-exposure dating, and optically-stimulated luminescence dating. Radiocarbon (14C) dating relies on the presence of organic material in an interpretable context within the alluvial deposit, which is rare in dry environments. Cosmogenic radionuclide (CRN) techniques require determination of the effects of pre-depositionally inherited radionuclides and post-depositional erosion of the target deposit, and proper calibration of isotope production rates. Optically-stimulated luminescence (OSL) dating shows great promise, but is still regarded as developmental in its application to fluvial deposits. I present results of a “blind” comparison of all three techniques (with emphasis on direct comparison of radiocarbon and OSL dating by two independent laboratories) applied to late-Pleistocene to late-Holocene axial-fluvial and alluvial-fan deposits in Cuyama Valley, in the western Transverse Ranges, California, USA. This study serves to highlight both limitations and successful applications of these techniques within a detailed case-study. This is not intend to be a comprehensive review of details of each dating technique; for a complete review of methodology and application of each 8 technique the reader is directed to publications such as Gosse and Phillips (2001) for CRN techniques, Wallinga (2002) and Aitken (1998) for OSL dating, and Faure (1986) for radiocarbon dating. This paper also does not detail the geologic interpretations made within the wider scope of the study, but instead focuses on the comparison of the geochronologic data. Appendix B presents geological interpretations made from the some of the results presented in Appendix A as well as additional field mapping and topographic analysis of alluvial fans in Cuyama Valley, California. Suites of inset alluvial fan surfaces found on mountain piedmonts in arid regions record episodic alluvial episodes caused by changes in upstream sediment and water flux. These episodes of increased piedmont sedimentation (and intervening times of fluvial entrenchment and lateral erosion) are widely thought of as caused by cyclic climate change. In regions where past climates have acted on distinct catchments in similar ways, these flights of terraces are often assumed to be age-equivalent. The causes of these alluvial episodes can be diverse. In desert regions (Wells, et al., 1987; Bull, 1991; Reheis et al., 1996; Harvey, et al., 1999; Ritter, et al., 2000; McDonald et al., 2003) and in at least one semi-arid to subhumid region (Weldon, 1986), changing hillslope vegetation and precipitation regime (increased storm intensity) during and after cool/wet to warm/dry climate transitions are most often cited as causing alluviation. In glaciated regions, drainage basin erosion by valley glaciers led to piedmont alluviation during
Load more

Recommended publications
  • Campground East of Highway
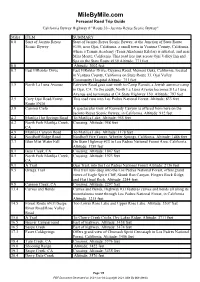
    MileByMile.com Personal Road Trip Guide California Byway Highway # "Route 33--Jacinto Reyes Scenic Byway" Miles ITEM SUMMARY 0.0 Start of Jacinto Reyes Start of Jacinto Reyes Scenic Byway, at the Junction of State Route Scenic Byway #150, near Ojai, California, a small town in Ventura County, California, where a Tennis Academy (Tenis Akademia Kilatas) is situated, and near Mira Monte, California. This road lies just across Ojai Valley Inn and Spa on the State Route #150 Altitude: 771 feet 0.0 Altitude: 3002 feet 0.7 East ElRoblar Drive East ElRoblar Drive, Cuyama Road, Meiners Oaks, California, located in Ventura County, California on State Route 33, Ojai Valley Community Hospital Altitude: 751 feet 1.5 North La Luna Avenue Fairview Road goes east-north to Camp Ramah, a Jewish summer camp in Ojai, CA. To the south, North La Luna Avenue becomes S La Luna Avenue and terminates at CA State Highway 150. Altitude: 797 feet 2.5 Cozy Ojai Road/Forest This road runs into Los Padres National Forest. Altitude: 833 feet Route 5N34 3.9 Camino Cielo A spectacular view of Kennedy Canyon is offered from here on the Jacinto Reyes Scenic Byway, in California. Altitude: 912 feet 4.2 Matilija Hot Springs Road To Matilija Lake. Altitude: 955 feet 4.2 North Fork Matilija Creek, Crossing. Altitude: 958 feet CA 4.9 Matilija Canyon Road To Matilija Lake. Altitude: 1178 feet 6.4 Nordhoff Ridge Road Nordhoff Fire Tower, Wheeler Springs, California. Altitude: 1486 feet 7.7 Blue Mist Water Fall On State Highway #33 in Los Padres National Forest Area, California.
    [Show full text]
  • Sediment Provenance and Dispersal of Neogene–Quaternary Strata of the Southeastern San Joaquin Basin and Its Transition Into the GEOSPHERE; V
    Research Paper THEMED ISSUE: Origin and Evolution of the Sierra Nevada and Walker Lane GEOSPHERE Sediment provenance and dispersal of Neogene–Quaternary strata of the southeastern San Joaquin Basin and its transition into the GEOSPHERE; v. 12, no. 6 southern Sierra Nevada, California doi:10.1130/GES01359.1 Jason Saleeby1, Zorka Saleeby1, Jason Robbins2, and Jan Gillespie3 13 figures; 2 tables; 2 supplemental files 1Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, California 91125, USA 2Chevron North America Exploration and Production, McKittrick, California 93251, USA 3Department of Geological Sciences, California State University, Bakersfield, California 93311, USA CORRESPONDENCE: jason@ gps .caltech .edu CITATION: Saleeby, J., Saleeby, Z., Robbins, J., and ABSTRACT INTRODUCTION Gillespie, J., 2016, Sediment provenance and dis- persal of Neogene–Quaternary strata of the south- eastern San Joaquin Basin and its transition into We have studied detrital-zircon U-Pb age spectra and conglomerate clast The Sierra Nevada and Great Valley of California are structurally coupled the southern Sierra Nevada, California: Geosphere, populations from Neogene–Quaternary siliciclastic and volcaniclastic strata and move semi-independently within the San Andreas–Walker Lane dextral v. 12, no. 6, p. 1744–1773, doi:10.1130/GES01359.1. of the southeastern San Joaquin Basin, as well as a fault-controlled Neo- transform system as a microplate (Argus and Gordon, 1991; Unruh et al., 2003). gene basin that formed across the southernmost Sierra Nevada; we call this Regional relief generation and erosion of the Sierra Nevada are linked to sub- Received 9 May 2016 Accepted 31 August 2016 basin the Walker graben.
    [Show full text]
  • Geology and Ground-Water Features of the Edison-Maricopa Area Kern County, California
    Geology and Ground-Water Features of the Edison-Maricopa Area Kern County, California By P. R. WOOD and R. H. DALE GEOLOGICAL SURVEY WATER-SUPPLY PAPER 1656 Prepared in cooperation with the California Department of Heater Resources UNITED STATES GOVERNMENT PRINTING OFFICE, WASHINGTON : 1964 UNITED STATES DEPARTMENT OF THE INTERIOR STEWART L. UDALL, Secretary GEOLOGICAL SURVEY Thomas B. Nolan, Director The U.S. Geological Survey Library catalog card for tbis publication appears on page following tbe index. For sale by the Superintendent of Documents, U.S. Government Printing Office Washington, D.C. 20402 CONTENTS Page Abstract______________-_______----_-_._________________________ 1 Introduction._________________________________-----_------_-______ 3 The water probiem-________--------------------------------__- 3 Purpose of the investigation.___________________________________ 4 Scope and methods of study.___________________________________ 5 Location and general features of the area_________________________ 6 Previous investigations.________________________________________ 8 Acknowledgments. ____________________________________________ 9 Well-numbering system._______________________________________ 9 Geography ___________________________________________________ 11 Climate.__-________________-____-__------_-----_---_-_-_----_ 11 Physiography_..__________________-__-__-_-_-___-_---_-----_-_- 14 General features_________________________________________ 14 Sierra Nevada___________________________________________ 15 Tehachapi Mountains..---.________________________________
    [Show full text]
  • Region of the San Andreas Fault, Western Transverse Ranges, California
    Thrust-Induced Collapse of Mountains— An Example from the “Big Bend” Region of the San Andreas Fault, Western Transverse Ranges, California By Karl S. Kellogg Scientific Investigations Report 2004–5206 U.S. Department of the Interior U.S. Geological Survey U.S. Department of the Interior Gale A. Norton, Secretary U.S. Geological Survey Charles G. Groat, Director U.S. Geological Survey, Reston, Virginia: 2004 For sale by U.S. Geological Survey, Information Services Box 25286, Denver Federal Center Denver, CO 80225 For more information about the USGS and its products: Telephone: 1-888-ASK-USGS World Wide Web: http://www.usgs.gov/ Any use of trade, product, or firm names in this publication is for descriptive purposes only and does not imply endorsement by the U.S. Government. Although this report is in the public domain, permission must be secured from the individual copyright owners to reproduce any copyrighted materials contained within this report. iii Contents Abstract ……………………………………………………………………………………… 1 Introduction …………………………………………………………………………………… 1 Geology of the Mount Pinos and Frazier Mountain Region …………………………………… 3 Fracturing of Crystalline Rocks in the Hanging Wall of Thrusts ……………………………… 5 Worldwide Examples of Gravitational Collapse ……………………………………………… 6 A Spreading Model for Mount Pinos and Frazier Mountain ………………………………… 6 Conclusions …………………………………………………………………………………… 8 Acknowledgments …………………………………………………………………………… 8 References …………………………………………………………………………………… 8 Illustrations 1. Regional geologic map of the western Transverse Ranges of southern California …………………………………………………………………………… 2 2. Simplified geologic map of the Mount Pinos-Frazier Mountain region …………… 2 3. View looking southeast across the San Andreas rift valley toward Frazier Mountain …………………………………………………………………… 3 4. View to the northwest of Mount Pinos, the rift valley (Cuddy Valley) of the San Andreas fault, and the trace of the Lockwood Valley fault ……………… 3 5.
    [Show full text]
  • Abridged Vita 2012
    ABRIDGED VITA 2012 EDWARD A. KELLER Environmental Studies and Department of Earth Science University of California Santa Barbara, California 93106 Keller, Edward A. (1942-) Earth Surface Processes, Engineering Geology, Environmental Geology University of California, Santa Barbara, June 17,2009. Statement by A. E. Gates (2003)1 When an earthquake occurs in the eastern or central part of the United States there are seismic waves that shake buildings and other structures but rarely is there evidence on the surface as to where it occurred. Instead the only way to locate the earthquake is with seismographs and patterns of seismic activity are as uncommon as the surface features. For that reason, geomorphology is regarded as a rather gentle branch of geology there. In the western United States on the other hand, earthquakes and other tectonic movements leave scars, induce landslides and generally wreak havoc on buildings and people. In stark contrast to the east, tectonic geomorphology is a dynamic and dangerous study. Edward Keller is one of the foremost experts on tectonic geomorphology especially with regard to earthquake reduction and prevention. By studying relative uplift and subsidence both in terms of rates and elevation changes, tectonic movements and their extent and intensity may be revealed. The beautiful wave cut terraces of the California Pacific coast are excellent examples of the types of features that Keller studies. They reveal sequential tectonic uplift of the land surface with erosion during the quiet periods. Such studies can reveal information on recurrence intervals for earthquakes, potential for blind faults, as well as landslides and other hazards.
    [Show full text]
  • Insights from Lowtemperature Thermochronometry Into
    TECTONICS, VOL. 32, 1602–1622, doi:10.1002/2013TC003377, 2013 Insights from low-temperature thermochronometry into transpressional deformation and crustal exhumation along the San Andreas fault in the western Transverse Ranges, California Nathan A. Niemi,1 Jamie T. Buscher,2 James A. Spotila,3 Martha A. House,4 and Shari A. Kelley 5 Received 21 May 2013; revised 21 October 2013; accepted 28 October 2013; published 20 December 2013. [1] The San Emigdio Mountains are an example of an archetypical, transpressional structural system, bounded to the south by the San Andreas strike-slip fault, and to the north by the active Wheeler Ridge thrust. Apatite (U-Th)/He and apatite and zircon fission track ages were obtained along transects across the range and from wells in and to the north of the range. Apatite (U-Th)/He ages are 4–6 Ma adjacent to the San Andreas fault, and both (U-Th)/He and fission track ages grow older with distance to the north from the San Andreas. The young ages north of the San Andreas fault contrast with early Miocene (U-Th)/He ages from Mount Pinos on the south side of the fault. Restoration of sample paleodepths in the San Emigdio Mountains using a regional unconformity at the base of the Eocene Tejon Formation indicates that the San Emigdio Mountains represent a crustal fragment that has been exhumed more than 5 km along the San Andreas fault since late Miocene time. Marked differences in the timing and rate of exhumation between the northern and southern sides of the San Andreas fault are difficult to reconcile with existing structural models of the western Transverse Ranges as a thin-skinned thrust system.
    [Show full text]
  • ELK CONSERVATION and MANAGEMENT PLAN December 2018 CONTENTS
    ELK CONSERVATION AND MANAGEMENT PLAN December 2018 CONTENTS EXECUTIVE SUMMARY 4 I. INTRODUCTION 10 A. Goals and Objectives 13 B. Taxonomy and Historical Distribution 15 C. Life History and Habitat 18 D. Distribution and Population Status Since 1970 22 E. Historical and Ongoing Management Efforts by the Department and California Tribes 30 II. CONSERVATION AND MANAGEMENT 32 A. Adaptive Management 32 B. Population Monitoring 33 C. Population Viability and Genetic Diversity 36 D. Disease Surveillance 38 E. Co-Management with California Federally Recognized Tribes & Tribal Traditional Uses and Knowledge 40 F. Hunting 41 G. Depredation Response and Alleviation 43 H. Human Dimensions 44 2 III. UNRESOLVED MANAGEMENT ISSUES AND INFORMATION NEEDS 45 A. Key Uncertainties 45 B. Research Needs to Inform Management 49 IV. MANAGEMENT ACTIONS 53 A. Strategy for Implementation and Evaluation 53 B. Priority Actions 53 V. PLAN REVIEW AND REVISION 54 VI. LITERATURE CITED 55 VII. GLOSSARY OF ACRONYMS AND TERMS 66 VIII. LIST OF FIGURES and TABLES 67 IX. APPENDICES 68 3 FROM OUR DIRECTOR It is remarkable that in a state with nearly 40 million people, one of the largest, most iconic land mammals in North America is one of our most successful conservation stories. Elk, or Wapiti, meaning “ghost kings” as named by the Shawnee Indians due to the animals’ elusive behavior are coming back from a precipitous population decline. The Department of Fish and Wildlife is proud to present this adaptive, scientifically based management plan that considers the many challenges facing elk in the most populous state in the nation. We’ve come a long way.
    [Show full text]
  • Aliso, 34(2), Online Supplement ISSN 0065-6275 (Print), ISSN 2327-2929 (Online)
    Aliso, 34(2), Online Supplement ISSN 0065-6275 (print), ISSN 2327-2929 (online) Online Supplement for “Tomus Nominum Eriastri: The Nomenclature and Taxonomy of Eriastrum (Polemoniaceae: Loeselieae)”, Sarah J. De Groot (2016) Aliso: A Journal of Systematic and Evolutionary Botany 34 (2): 25–152. EXSICCATAE Representative specimens studied. Not all associate collectors are listed. Eriastrum abramsii JEPS116786. Along Vineyard Canyon Road just over 14 miles north U.S.A. CALIFORNIA: Lake County: Kelseyville, 15 May 1924, J.W. of Monterey-San Luis Obispo county line, 31 May 2008, S.J. De Groot Blankinship s.n., CAS165485. Mt. Konocti [near Kelseyville], 4 Jun 5879, RSA (Pop 260). San Benito County: West of Coalinga, dry 1929, J.W. Blankinship s.n., POM279114. Ridge between Burns hillside, 13 Jun 1910, I.J. Condit s.n., UC455635. Coalinga Road near Valley and Borax Lake, 12 May 1945, H.L. Mason 12585, DS342729. mile post 9.82 from its junction with Highway 25 and east of 2.5 miles south of Kelseyville, 28 Jun 1945, H.L. Mason 12606, Bitterwater, 15 Jun 2004, D. Gowen 117, JEPS105711, JEPS105712. DS342491. 2.5 miles south of Kelseyville on road to Lower Lake, 28 Coalinga Road east of Highway 25 and Bitterwater, near milepost Jun 1945, M.S. Baker 11081, CAS326268. S-facing slope ca. 1 mile 9.82, 1 Jun 2006, D. Gowen 597, JEPS116802. Along Coalinga Road WSW of Glenbrook, upper High Valley Cr. drainage, SE/4 of SW/4 at mile marker 9.82 from Highway 25, 1 Jun 2008, S.J. De Groot S32 T12N R8W, 1 Jun 1983, R.D.
    [Show full text]
  • The Metamorphic and Plutonic Rocks of the Southernmost Sierra Nevada, California, and Their Tectonic Framework
    The Metamorphic and Plutonic Rocks of the Southernmost Sierra Nevada, California, and Their Tectonic Framework U.S. GEOLOGICAL SURVEY PROFESSIONAL PAPER 1381 The Metamorphic and Plutonic Rocks of the Southernmost Sierra Nevada, California, and Their Tectonic Framework By DONALD C. ROSS U.S. GEOLOGICAL SURVEY PROFESSIONAL PAPER 1381 UNITED STATES GOVERNMENT PRINTING OFFICE, WASHINGTON : 1989 DEPARTMENT OF THE INTERIOR MANUEL LUJAN, JR., Secretary U.S. GEOLOGICAL SURVEY Dallas L. Peck, Director Any use of trade, product, or firm names in this publication is for descriptive purposes only and does not imply endorsement by the U.S. Government Library of Congress Cataloging-in-Publication Data Ross, Donald Clarence, 1924 The metamorphic and plutonic rocks of the southernmost Sierra Nevada, California, and their tectonic framework / by Donald C. Ross. p. cm. (U.S. Geological Survey professional paper ; 1381) Bibliography: p. Supt.ofDocs.no.: 119.16:1381 1. Rocks, Igneous Sierra Nevada Mountains (Calif, and Nev.) 2. Rocks, Metamorphic Sierra Nevada Mountains (Calif, and Nev.) I. Title. II. Series. QE461.R645 1989 552'.1'097944 dc20 89-6000136 CIP For sale by the Books and Open-File Reports Section U.S. Geological Survey, Federal Center, Box 25425, Denver, CO 80225 CONTENTS Abstract---------------------------- l Plutonic rocks- ------------------------ 23 Introduction- ------------------------- 1 Units north of the Garlock fault- ------------- 23 Acknowledgments----------------------- 3 Granitic rocks related(?) to the San Emigdio- Metamorphic
    [Show full text]
  • Analysis of Competing Hypotheses for the Tectonic Evolution of the Bakersfield Arch
    ANALYSIS OF COMPETING HYPOTHESES FOR THE TECTONIC EVOLUTION OF THE BAKERSFIELD ARCH by Jefferson Vasconcellos A Thesis Submitted to the Department of Geology California State University Bakersfield In Partial Fulfillment for the Degree of Masters of Petroleum Geology Winter 2016 Copyright By Jefferson Vasconcellos 2016 ANALYSIS OF COMPETING HYPOTHESES FOR THE TECTONIC EVOLUTION OF THE BAKERSFIELD ARCH By Jefferson Vasconcellos This thesis has been accepted on behalf of the Department of Geology by their supervisory committee: ' uf~i::;e,~¥&'f: . Professor of Geology Committee Chair Robert Negrini, PhD Professor of Geology Dirk Baron, PhD Department Chair, Professor of Geology ABSTRACT The widespread presence of Neogene and Quaternary units in the southeastern San Joaquin Valley provide evidence for the tectonic evolution of the Bakersfield Arch, an area of major oil production in California. The purpose of this study is to test two different age hypotheses for the uplift of the Arch: middle Miocene and late Quaternary. Electric log correlations of stratigraphic marker units were used to create isochore maps of sedimentary packages of various ages across the Arch. These data indicate that changes in horizontal distribution and thickness of stratigraphic units across the Arch are influenced by two distinct uplift events in the area: 1) during middle to late Miocene time and 2) latest Miocene (post-Etchegoin Formation deposition) to Pleistocene time. Future work incorporating more detailed correlation of individual chert markers within the Monterey Formation would more closely define the exact timing of the earlier episode of uplift in the area. Age diagnostic data are insufficient to determine the time of onset of the later period of uplift.
    [Show full text]
  • Tectonic Geomorphology of Active Folding Over Buried Reverse Faults: San Emigdio Mountain Front, Southern San Joaquin Valley, California
    Tectonic geomorphology of active folding over buried reverse faults: San Emigdio Mountain front, southern San Joaquin Valley, California E. A. Keller* Environmental Studies Program and Department of Geological Sciences, University of California, Santa Barbara, California 93106 D. B. Seaver SEPUP, Lawrence Hall of Science, University of California, Berkeley, California 94720 D. L. Laduzinsky Henshaw Associates, Inc., 11875 Dublin Boulevard, Suite A-200, Dublin, California 94568 D. L. Johnson Department of Geography, University of Illinois, Urbana, Illinois 61801 T. L. Ku Department of Earth Sciences, University of Southern California, Los Angeles, California 90089 ABSTRACT INTRODUCTION The objectives of the research presented in this paper are: (1) investigate the tectonic framework, Investigation of the tectonic geomorphol- This study was undertaken to determine the geometry, and range of vertical deformation rates ogy of active folding over buried reverse faults Quaternary history associated with the folding associated with folding on upper plates of buried at the San Emigdio Mountain front, southern and vertical deformation of the San Emigdio reverse faults, and (2) reconstruction of the Qua- San Joaquin Valley, California, provides in- Mountains. The study area (Fig. 1) is located ternary depositional and tectonic history of the sight concerning the tectonic and geomorphic near the boundary between two geomorphic north flank of the San Emigdio Mountain front. development of mountain fronts produced by provinces: the Transverse Ranges to the south We assume for our evaluation that tectonic ac- active folding and faulting. Monoclinally flexed and the San Joaquin Valley to the north. The tivity rather than climatic change has produced gravels with dips as great as 50º and a mini- east-west–trending San Emigdio Mountains, the observed vertical separation of Quaternary de- mum age of about 65 ka provide evidence of part of the southern Coast Ranges, cut across the posits and surfaces.
    [Show full text]
  • Cleveland National Forest
    Draft Supplemental Environmental Impact Statement Southern California National Forests Land Management Plan Amendment Appendix 2 Inventoried Roadless Area Analysis The Southern California National Forests Inventoried Roadless Area (IRA) Analysis (FSH 1909.12-2007-1, Chapter 72) for a Land Management Plan Amendment. The proposed Amendment is a result of the January 3, 2011 Settlement Agreement. This page left blank intentionally. Southern California National Forests Draft Supplemental Appendix 2 Land Management Plan Amendment Environmental Impact Statement Table of Contents Angeles National Forest ..............................................................................................................1 Fish Canyon Inventoried Roadless Area ..................................................................................1 Overview .............................................................................................................................1 Capability ............................................................................................................................2 Availability ..........................................................................................................................6 Need ....................................................................................................................................7 Angeles National Forest ..............................................................................................................9 Red Mountain Inventoried Roadless Area
    [Show full text]