DOCSLIB.ORG

The Quantum Mechanics of Two Dimensional Superfluids

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Quantum Mechanics of Two Dimensional Superfluids The quantum mechanics of two dimensional superfluids Physical Review B 71, 144508 and 144509 (2005), cond-mat/0502002 Leon Balents (UCSB) Lorenz Bartosch (Yale) Anton Burkov (UCSB) Subir Sachdev (Yale) Krishnendu Sengupta (Toronto) Talk online: Sachdev OutlineOutline I. Bose-Einstein condensation and superfluidity II. The superfluid-Mott insulator quantum phase transition III. The cuprate superconductors Superfluids proximate to finite doping Mott insulators with VBS order ? IV. Vortices in the superfluid V. Vortices in superfluids near the superfluid-insulator quantum phase transition The “quantum order” of the superconducting state: evidence for vortex flavors I. Bose-Einstein condensation and superfluidity Superfluidity/superconductivity occur in: • liquid 4He • metals Hg, Al, Pb, Nb, Nb3Sn….. • liquid 3He • neutron stars • cuprates La2-xSrxCuO4, YBa2Cu3O6+y…. •M3C60 • ultracold trapped atoms •MgB2 The Bose-Einstein condensate: A macroscopic number of bosons occupy the lowest energy quantum state Such a condensate also forms in systems of fermions, where the bosons are Cooper pairs of fermions: ky Pair wavefunction in cuprates: Ψ =−kk22↑↓−↓↑ k ()xy() x S = 0 Velocity distribution function of ultracold 87Rb atoms M. H. Anderson, J. R. Ensher, M. R. Matthews, C. E. Wieman and E. A. Cornell, Science 269, 198 (1995) Superflow: The wavefunction of the condensate iθ r Ψ→Ψe ( ) Superfluid velocity v = ∇θ s m (for non-Galilean invariant superfluids, the co-efficient of ∇θ is modified) II. The superfluid-Mott insulator quantum phase transition Apply a periodic potential (standing laser beams) to trapped ultracold bosons (87Rb) Momentum distribution function of bosons Bragg reflections of condensate at reciprocal lattice vectors M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, and I. Bloch, Nature 415, 39 (2002). Momentum distribution function of bosons Bragg reflections of condensate at reciprocal lattice vectors M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, and I. Bloch, Nature 415, 39 (2002). Superfluid-insulator quantum phase transition at T=0 V0=0Er V0=3Er V0=7Er V0=10Er V0=13Er V0=14Er V0=16Er V0=20Er Superfluid-insulator quantum phase transition at T=0 M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, and I. Bloch, Nature 415, 39 (2002). Bosons at filling fraction f = 1 Weak interactions: superfluidity Strong interactions: Mott insulator which preserves all lattice symmetries M. Greiner, O. Mandel, T. Esslinger, T. W. Hänsch, and I. Bloch, Nature 415, 39 (2002). Bosons at filling fraction f = 1 Ψ ≠ 0 Weak interactions: superfluidity Bosons at filling fraction f = 1 Ψ ≠ 0 Weak interactions: superfluidity Bosons at filling fraction f = 1 Ψ ≠ 0 Weak interactions: superfluidity Bosons at filling fraction f = 1 Ψ ≠ 0 Weak interactions: superfluidity Bosons at filling fraction f = 1 Ψ = 0 Strong interactions: insulator Bosons at filling fraction f = 1/2 Ψ ≠ 0 Weak interactions: superfluidity C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Bosons at filling fraction f = 1/2 Ψ ≠ 0 Weak interactions: superfluidity C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Bosons at filling fraction f = 1/2 Ψ ≠ 0 Weak interactions: superfluidity C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Bosons at filling fraction f = 1/2 Ψ ≠ 0 Weak interactions: superfluidity C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Bosons at filling fraction f = 1/2 Ψ ≠ 0 Weak interactions: superfluidity C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Bosons at filling fraction f = 1/2 Ψ = 0 Strong interactions: insulator C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Bosons at filling fraction f = 1/2 Ψ = 0 Strong interactions: insulator C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Insulating phases of bosons at filling fraction f = 1/2 1 = ( + ) 2 Charge density Valence bond Valence bond wave (CDW) order solid (VBS) order solid (VBS) order iQr. Can define a common CDW/VBS order using a generalized "density" ρρ(r ) = ∑ Qe Q All insulators have Ψ=0 and ρQ ≠0 for certain Q C. Lannert, M.P.A. Fisher, and T. Senthil, Phys. Rev. B 63, 134510 (2001) S. Sachdev and K. Park, Annals of Physics, 298, 58 (2002) Superfluid-insulator transition of bosons at generic filling fraction f The transition is characterized by multiple distinct order parameters (boson condensate, VBS/CDW order) Traditional (Landau-Ginzburg-Wilson) view: Such a transition is first order, and there are no precursor fluctuations of the order of the insulator in the superfluid.
Load more

Recommended publications
  • Φ0-Magnetic Force Microscopy for Imaging and Control of Vortex
    Imaging and controlling vortex dynamics in mesoscopic superconductor-normal-metal-superconductor arrays Tyler R. Naibert1, Hryhoriy Polshyn1,2,*, Rita Garrido-Menacho1, Malcolm Durkin1, Brian Wolin1, Victor Chua1, Ian Mondragon-Shem1, Taylor Hughes1, Nadya Mason1,*, and Raffi Budakian1,3 1Department of Physics, University of Illinois at Urbana-Champaign, 1110 W. Green St., Urbana, IL 61801-3080, USA 2Department of Physics, University of California, Santa Barbara, CA 93106, USA 3Institute for Quantum Computing, University of Waterloo, Waterloo, ON, Canada, N2L3G1 Department of Physics, University of Waterloo, Waterloo, ON, Canada, N2L3G1 Perimeter Institute for Theoretical Physics, Waterloo, ON, Canada, N2L2Y5 Canadian Institute for Advanced Research, Toronto, ON, Canada, M5G1Z8 *Corresponding authors. Email: [email protected]; [email protected] Harnessing the properties of vortices in superconductors is crucial for fundamental science and technological applications; thus, it has been an ongoing goal to locally probe and control vortices. Here, we use a scanning probe technique that enables studies of vortex dynamics in superconducting systems by leveraging the resonant behavior of a raster-scanned, magnetic-tipped cantilever. This experimental setup allows us to image and control vortices, as well as extract key energy scales of the vortex interactions. Applying this technique to lattices of superconductor island arrays on a metal, we obtain a variety of striking spatial patterns that encode information about the energy landscape for vortices in the system. We interpret these patterns in terms of local vortex dynamics and extract the relative strengths of the characteristic energy scales in the system, such as the vortex-magnetic field and vortex-vortex interaction strengths, as well as the vortex chemical potential.
    [Show full text]
  • Scanning Hall Probe Microscopy of Vortex Matter in Single-And Two-Gap Superconductors
    ARENBERG DOCTORAL SCHOOL Faculty of Science Scanning Hall probe microscopy of vortex matter in single-and two-gap superconductors - Bart Raes Promotors: Dissertation presented in partial Prof.Dr. Victor V. Moshchalkov fulfillment of the requirements for the Prof.Dr. Jacques Tempère PhD degree July 2013 Scanning Hall probe microscopy of vortex matter in single-and two-gap superconductors Bart RAES Dissertation presented in partial fulfillment of the requirements for the PhD degree Members of the Examination committee: Prof. Dr. Victor V. Moshchalkov KU Leuven (Promotor) Prof. Dr. Jacques Tempère Universiteit Antwerpen (Co-promotor) Prof. Dr. J. Van de Vondel KU Leuven (Secretary) Prof. Dr. L. Chibotaru KU Leuven (President) Prof. Dr. J. Vanacken KU Leuven Dr. J. Gutierrez Royo KU Leuven Prof. Dr. A.V. Silhanek Université de Liège Prof. Dr. S. Bending University of Bath Prof. Dr. G. Borghs KU Leuven, IMEC July 2013 © 2013 KU Leuven, Groep Wetenschap & Technologie, Arenberg Doctoraatsschool, W. de Croylaan 6, 3001 Leuven, België Alle rechten voorbehouden. Niets uit deze uitgave mag worden vermenigvuldigd en/of openbaar gemaakt worden door middel van druk, fotocopie, microfilm, elektronisch of op welke andere wijze ook zonder voorafgaande schriftelijke toestemming van de uitgever. All rights reserved. No part of the publication may be reproduced in any form by print, photoprint, microfilm or any other means without written permission from the publisher. ISBN 978-90-8649-638-9 D/2013/10.705/53 Dankwoord-Acknowledgements Doctoreren is niet alleen het resultaat van bijna vier jaar wetenschappelijk onderzoek, het is een lange weg met veel hindernissen maar zeker ook enkele hoogtepunten.
    [Show full text]
  • Lecture 3: Fermi-Liquid Theory 1 General Considerations Concerning Condensed Matter
    Phys 769 Selected Topics in Condensed Matter Physics Summer 2010 Lecture 3: Fermi-liquid theory Lecturer: Anthony J. Leggett TA: Bill Coish 1 General considerations concerning condensed matter (NB: Ultracold atomic gasses need separate discussion) Assume for simplicity a single atomic species. Then we have a collection of N (typically 1023) nuclei (denoted α,β,...) and (usually) ZN electrons (denoted i,j,...) interacting ∼ via a Hamiltonian Hˆ . To a first approximation, Hˆ is the nonrelativistic limit of the full Dirac Hamiltonian, namely1 ~2 ~2 1 e2 1 Hˆ = 2 2 + NR −2m ∇i − 2M ∇α 2 4πǫ r r α 0 i j Xi X Xij | − | 1 (Ze)2 1 1 Ze2 1 + . (1) 2 4πǫ0 Rα Rβ − 2 4πǫ0 ri Rα Xαβ | − | Xiα | − | For an isolated atom, the relevant energy scale is the Rydberg (R) – Z2R. In addition, there are some relativistic effects which may need to be considered. Most important is the spin-orbit interaction: µ Hˆ = B σ (v V (r )) (2) SO − c2 i · i × ∇ i Xi (µB is the Bohr magneton, vi is the velocity, and V (ri) is the electrostatic potential at 2 3 2 ri as obtained from HˆNR). In an isolated atom this term is o(α R) for H and o(Z α R) for a heavy atom (inner-shell electrons) (produces fine structure). The (electron-electron) magnetic dipole interaction is of the same order as HˆSO. The (electron-nucleus) hyperfine interaction is down relative to Hˆ by a factor µ /µ 10−3, and the nuclear dipole-dipole SO n B ∼ interaction by a factor (µ /µ )2 10−6.
    [Show full text]
  • Phys 446: Solid State Physics / Optical Properties Lattice Vibrations
    Solid State Physics Lecture 5 Last week: Phys 446: (Ch. 3) • Phonons Solid State Physics / Optical Properties • Today: Einstein and Debye models for thermal capacity Lattice vibrations: Thermal conductivity Thermal, acoustic, and optical properties HW2 discussion Fall 2007 Lecture 5 Andrei Sirenko, NJIT 1 2 Material to be included in the test •Factors affecting the diffraction amplitude: Oct. 12th 2007 Atomic scattering factor (form factor): f = n(r)ei∆k⋅rl d 3r reflects distribution of electronic cloud. a ∫ r • Crystalline structures. 0 sin()∆k ⋅r In case of spherical distribution f = 4πr 2n(r) dr 7 crystal systems and 14 Bravais lattices a ∫ n 0 ∆k ⋅r • Crystallographic directions dhkl = 2 2 2 1 2 ⎛ h k l ⎞ 2πi(hu j +kv j +lw j ) and Miller indices ⎜ + + ⎟ •Structure factor F = f e ⎜ a2 b2 c2 ⎟ ∑ aj ⎝ ⎠ j • Definition of reciprocal lattice vectors: •Elastic stiffness and compliance. Strain and stress: definitions and relation between them in a linear regime (Hooke's law): σ ij = ∑Cijklε kl ε ij = ∑ Sijklσ kl • What is Brillouin zone kl kl 2 2 C •Elastic wave equation: ∂ u C ∂ u eff • Bragg formula: 2d·sinθ = mλ ; ∆k = G = eff x sound velocity v = ∂t 2 ρ ∂x2 ρ 3 4 • Lattice vibrations: acoustic and optical branches Summary of the Last Lecture In three-dimensional lattice with s atoms per unit cell there are Elastic properties – crystal is considered as continuous anisotropic 3s phonon branches: 3 acoustic, 3s - 3 optical medium • Phonon - the quantum of lattice vibration. Elastic stiffness and compliance tensors relate the strain and the Energy ħω; momentum ħq stress in a linear region (small displacements, harmonic potential) • Concept of the phonon density of states Hooke's law: σ ij = ∑Cijklε kl ε ij = ∑ Sijklσ kl • Einstein and Debye models for lattice heat capacity.
    [Show full text]
  • Chapter 3 Bose-Einstein Condensation of an Ideal
    Chapter 3 Bose-Einstein Condensation of An Ideal Gas An ideal gas consisting of non-interacting Bose particles is a ¯ctitious system since every realistic Bose gas shows some level of particle-particle interaction. Nevertheless, such a mathematical model provides the simplest example for the realization of Bose-Einstein condensation. This simple model, ¯rst studied by A. Einstein [1], correctly describes important basic properties of actual non-ideal (interacting) Bose gas. In particular, such basic concepts as BEC critical temperature Tc (or critical particle density nc), condensate fraction N0=N and the dimensionality issue will be obtained. 3.1 The ideal Bose gas in the canonical and grand canonical ensemble Suppose an ideal gas of non-interacting particles with ¯xed particle number N is trapped in a box with a volume V and at equilibrium temperature T . We assume a particle system somehow establishes an equilibrium temperature in spite of the absence of interaction. Such a system can be characterized by the thermodynamic partition function of canonical ensemble X Z = e¡¯ER ; (3.1) R where R stands for a macroscopic state of the gas and is uniquely speci¯ed by the occupa- tion number ni of each single particle state i: fn0; n1; ¢ ¢ ¢ ¢ ¢ ¢g. ¯ = 1=kBT is a temperature parameter. Then, the total energy of a macroscopic state R is given by only the kinetic energy: X ER = "ini; (3.2) i where "i is the eigen-energy of the single particle state i and the occupation number ni satis¯es the normalization condition X N = ni: (3.3) i 1 The probability
    [Show full text]
  • High Pressure Band Structure, Density of States, Structural Phase Transition and Metallization in Cds
    Chemical and Materials Engineering 5(1): 8-13, 2017 http://www.hrpub.org DOI: 10.13189/cme.2017.050102 High Pressure Band Structure, Density of States, Structural Phase Transition and Metallization in CdS J. Jesse Pius1, A. Lekshmi2, C. Nirmala Louis2,* 1Rohini College of Engineering, Nagercoil, Kanyakumari District, India 2Research Center in Physics, Holy Cross College, India Copyright©2017 by authors, all rights reserved. Authors agree that this article remains permanently open access under the terms of the Creative Commons Attribution License 4.0 International License Abstract The electronic band structure, density of high pressure studies due to the development of different states, metallization and structural phase transition of cubic designs of diamond anvil cell (DAC). With a modern DAC, zinc blende type cadmium sulphide (CdS) is investigated it is possible to reach pressures of 2 Mbar (200 GPa) using the full potential linear muffin-tin orbital (FP-LMTO) routinely and pressures of 5 Mbar (500 GPa) or higher is method. The ground state properties and band gap values achievable [3]. At such pressures, materials are reduced to are compared with the experimental results. The fractions of their original volumes. With this reduction in equilibrium lattice constant, bulk modulus and its pressure inter atomic distances; significant changes in bonding and derivative and the phase transition pressure at which the structure as well as other properties take place. The increase compounds undergo structural phase transition from ZnS to of pressure means the significant decrease in volume, which NaCl are predicted from the total energy calculations. The results in the change of electronic states and crystal structure.
    [Show full text]
  • Lecture 24. Degenerate Fermi Gas (Ch
    Lecture 24. Degenerate Fermi Gas (Ch. 7) We will consider the gas of fermions in the degenerate regime, where the density n exceeds by far the quantum density nQ, or, in terms of energies, where the Fermi energy exceeds by far the temperature. We have seen that for such a gas μ is positive, and we’ll confine our attention to the limit in which μ is close to its T=0 value, the Fermi energy EF. ~ kBT μ/EF 1 1 kBT/EF occupancy T=0 (with respect to E ) F The most important degenerate Fermi gas is 1 the electron gas in metals and in white dwarf nε()(),, T= f ε T = stars. Another case is the neutron star, whose ε⎛ − μ⎞ exp⎜ ⎟ +1 density is so high that the neutron gas is ⎝kB T⎠ degenerate. Degenerate Fermi Gas in Metals empty states ε We consider the mobile electrons in the conduction EF conduction band which can participate in the charge transport. The band energy is measured from the bottom of the conduction 0 band. When the metal atoms are brought together, valence their outer electrons break away and can move freely band through the solid. In good metals with the concentration ~ 1 electron/ion, the density of electrons in the electron states electron states conduction band n ~ 1 electron per (0.2 nm)3 ~ 1029 in an isolated in metal electrons/m3 . atom The electrons are prevented from escaping from the metal by the net Coulomb attraction to the positive ions; the energy required for an electron to escape (the work function) is typically a few eV.
    [Show full text]
  • Lecture Notes for Quantum Matter
    Lecture Notes for Quantum Matter MMathPhys c Professor Steven H. Simon Oxford University July 24, 2019 Contents 1 What we will study 1 1.1 Bose Superfluids (BECs, Superfluid He, Superconductors) . .1 1.2 Theory of Fermi Liquids . .2 1.3 BCS theory of superconductivity . .2 1.4 Special topics . .2 2 Introduction to Superfluids 3 2.1 Some History and Basics of Superfluid Phenomena . .3 2.2 Landau and the Two Fluid Model . .6 2.2.1 More History and a bit of Physics . .6 2.2.2 Landau's Two Fluid Model . .7 2.2.3 More Physical Effects and Their Two Fluid Pictures . .9 2.2.4 Second Sound . 12 2.2.5 Big Questions Remaining . 13 2.3 Curl Free Constraint: Introducing the Superfluid Order Parameter . 14 2.3.1 Vorticity Quantization . 15 2.4 Landau Criterion for Superflow . 17 2.5 Superfluid Density . 20 2.5.1 The Andronikoshvili Experiment . 20 2.5.2 Landau's Calculation of Superfluid Density . 22 3 Charged Superfluid ≈ Superconductor 25 3.1 London Theory . 25 3.1.1 Meissner-Ochsenfeld Effect . 27 3 3.1.2 Quantum Input and Superfluid Order Parameter . 29 3.1.3 Superconducting Vortices . 30 3.1.4 Type I and Type II superconductors . 32 3.1.5 How big is Hc ............................... 33 4 Microscopic Theory of Bosons 37 4.1 Mathematical Preliminaries . 37 4.1.1 Second quantization . 37 4.1.2 Coherent States . 38 4.1.3 Multiple orbitals . 40 4.2 BECs and the Gross-Pitaevskii Equation . 41 4.2.1 Noninteracting BECs as Coherent States .
    [Show full text]
  • Chapter 13 Ideal Fermi
    Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k T µ,βµ 1, B � � which defines the degenerate Fermi gas. In this limit, the quantum mechanical nature of the system becomes especially important, and the system has little to do with the classical ideal gas. Since this chapter is devoted to fermions, we shall omit in the following the subscript ( ) that we used for the fermionic statistical quantities in the previous chapter. − 13.1 Equation of state Consider a gas ofN non-interacting fermions, e.g., electrons, whose one-particle wave- functionsϕ r(�r) are plane-waves. In this case, a complete set of quantum numbersr is given, for instance, by the three cartesian components of the wave vector �k and thez spin projectionm s of an electron: r (k , k , k , m ). ≡ x y z s Spin-independent Hamiltonians. We will consider only spin independent Hamiltonian operator of the type ˆ 3 H= �k ck† ck + d r V(r)c r†cr , �k � where thefirst and the second terms are respectively the kinetic and th potential energy. The summation over the statesr (whenever it has to be performed) can then be reduced to the summation over states with different wavevectork(p=¯hk): ... (2s + 1) ..., ⇒ r � �k where the summation over the spin quantum numberm s = s, s+1, . , s has been taken into account by the prefactor (2s + 1). − − 159 160 CHAPTER 13. IDEAL FERMI GAS Wavefunctions in a box. We as- sume that the electrons are in a vol- ume defined by a cube with sidesL x, Ly,L z and volumeV=L xLyLz.
    [Show full text]
  • Density of States
    Density of states A Material is known to have a high density of states at the Fermi energy. (a) What does this tell you about the electrical, thermal and optical properties of this material? (b) Which of the following quasiparticles would you expect to observe in this material? (phonons, bipolarons, excitons, polaritons, suface plasmons) Why? (a): A high density of states at the fermi energy means that this material is a good electrical conductor. The specific heat can be calculated via the internal energy. Z 1 Z 1 E · D(E) u(E; T ) = E · D(E) · f(E)dE = dE (1) −∞ −∞ 1 + exp E−µ kB ·T du We know that cv = dT . So we get the following expression: E−µ 1 Z E · D(E) · (E − µ) · exp k T c = B dE (2) v 2 −∞ 2 E−µ kBT 1 + exp kbT Hence we deal with a metal, we will have a good thermal conductor because of the phonon and electron contribution. Light will get reflected out below the plasma frequency !P . (b): Due to fact that phonons describe lattice vibrations, it is possible to observe them in this material. They can be measured with an EELS experiment or with Raman Spectroscopy. A polaron describes a local polarisation of a crystal due to moving electrons. They are observable in materials with a low electron density and describe a charge-phonon coupling. There are two different kinds of polarons, the Fr¨ohlich Polaron and the Holstein Polaron. The Fr¨ohlich polarons describe large polarons, that means the distortion is much larger than the lattice constant of the material so that a lot of atoms are involved.
    [Show full text]
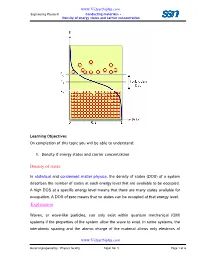
  • Density of States Explanation
    www.Vidyarthiplus.com Engineering Physics-II Conducting materials- - Density of energy states and carrier concentration Learning Objectives On completion of this topic you will be able to understand: 1. Density if energy states and carrier concentration Density of states In statistical and condensed matter physics , the density of states (DOS) of a system describes the number of states at each energy level that are available to be occupied. A high DOS at a specific energy level means that there are many states available for occupation. A DOS of zero means that no states can be occupied at that energy level. Explanation Waves, or wave-like particles, can only exist within quantum mechanical (QM) systems if the properties of the system allow the wave to exist. In some systems, the interatomic spacing and the atomic charge of the material allows only electrons of www.Vidyarthiplus.com Material prepared by: Physics faculty Topic No: 5 Page 1 of 6 www.Vidyarthiplus.com Engineering Physics-II Conducting materials- - Density of energy states and carrier concentration certain wavelengths to exist. In other systems, the crystalline structure of the material allows waves to propagate in one direction, while suppressing wave propagation in another direction. Waves in a QM system have specific wavelengths and can propagate in specific directions, and each wave occupies a different mode, or state. Because many of these states have the same wavelength, and therefore share the same energy, there may be many states available at certain energy levels, while no states are available at other energy levels. For example, the density of states for electrons in a semiconductor is shown in red in Fig.
    [Show full text]
  • Optical Properties and Electronic Density of States* 1 ( Manuel Cardona2 > Brown University, Providence, Rhode Island and DESY, Homburg, Germany
    t JOU RN AL O F RESEAR CH of th e National Bureau of Sta ndards -A. Ph ysics and Chemistry j Vol. 74 A, No.2, March- April 1970 7 Optical Properties and Electronic Density of States* 1 ( Manuel Cardona2 > Brown University, Providence, Rhode Island and DESY, Homburg, Germany (October 10, 1969) T he fundame nta l absorption spectrum of a so lid yie lds information about critical points in the opti· cal density of states. This informati on can be used to adjust parameters of the band structure. Once the adju sted band structure is known , the optical prope rties and the de nsity of states can be generated by nume ri cal integration. We revi ew in this paper the para metrization techniques used for obtaining band structures suitable for de nsity of s tates calculations. The calculated optical constants are compared with experim enta l results. The e ne rgy derivative of these opti cal constants is di scussed in connection with results of modulated re fl ecta nce measure ments. It is also shown that information about de ns ity of e mpty s tates can be obtained fro m optical experime nt s in vo lving excit ati on from dee p core le ve ls to the conduction band. A deta il ed comparison of the calc ul ate d one·e lectron opti cal line s hapes with experime nt reveals deviations whi ch can be interpre ted as exciton effects. The acc umulating ex pe rime nt al evide nce poin t· in g in this direction is reviewed togethe r with the ex isting theo ry of these effects.
    [Show full text]