A Generalization of Fermats Last Theorem: the Beal Conjecture And
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Scalar Curvature and Geometrization Conjectures for 3-Manifolds
Comparison Geometry MSRI Publications Volume 30, 1997 Scalar Curvature and Geometrization Conjectures for 3-Manifolds MICHAEL T. ANDERSON Abstract. We first summarize very briefly the topology of 3-manifolds and the approach of Thurston towards their geometrization. After dis- cussing some general properties of curvature functionals on the space of metrics, we formulate and discuss three conjectures that imply Thurston’s Geometrization Conjecture for closed oriented 3-manifolds. The final two sections present evidence for the validity of these conjectures and outline an approach toward their proof. Introduction In the late seventies and early eighties Thurston proved a number of very re- markable results on the existence of geometric structures on 3-manifolds. These results provide strong support for the profound conjecture, formulated by Thur- ston, that every compact 3-manifold admits a canonical decomposition into do- mains, each of which has a canonical geometric structure. For simplicity, we state the conjecture only for closed, oriented 3-manifolds. Geometrization Conjecture [Thurston 1982]. Let M be a closed , oriented, 2 prime 3-manifold. Then there is a finite collection of disjoint, embedded tori Ti 2 in M, such that each component of the complement M r Ti admits a geometric structure, i.e., a complete, locally homogeneous RiemannianS metric. A more detailed description of the conjecture and the terminology will be given in Section 1. A complete Riemannian manifold N is locally homogeneous if the universal cover N˜ is a complete homogenous manifold, that is, if the isometry group Isom N˜ acts transitively on N˜. It follows that N is isometric to N=˜ Γ, where Γ is a discrete subgroup of Isom N˜, which acts freely and properly discontinuously on N˜. -

Generalized Riemann Hypothesis Léo Agélas
Generalized Riemann Hypothesis Léo Agélas To cite this version: Léo Agélas. Generalized Riemann Hypothesis. 2019. hal-00747680v3 HAL Id: hal-00747680 https://hal.archives-ouvertes.fr/hal-00747680v3 Preprint submitted on 29 May 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Generalized Riemann Hypothesis L´eoAg´elas Department of Mathematics, IFP Energies nouvelles, 1-4, avenue de Bois-Pr´eau,F-92852 Rueil-Malmaison, France Abstract (Generalized) Riemann Hypothesis (that all non-trivial zeros of the (Dirichlet L-function) zeta function have real part one-half) is arguably the most impor- tant unsolved problem in contemporary mathematics due to its deep relation to the fundamental building blocks of the integers, the primes. The proof of the Riemann hypothesis will immediately verify a slew of dependent theorems (Borwien et al.(2008), Sabbagh(2002)). In this paper, we give a proof of Gen- eralized Riemann Hypothesis which implies the proof of Riemann Hypothesis and Goldbach's weak conjecture (also known as the odd Goldbach conjecture) one of the oldest and best-known unsolved problems in number theory. 1. Introduction The Riemann hypothesis is one of the most important conjectures in math- ematics. -

Towards the Poincaré Conjecture and the Classification of 3-Manifolds John Milnor
Towards the Poincaré Conjecture and the Classification of 3-Manifolds John Milnor he Poincaré Conjecture was posed ninety- space SO(3)/I60 . Here SO(3) is the group of rota- nine years ago and may possibly have tions of Euclidean 3-space, and I60 is the subgroup been proved in the last few months. This consisting of those rotations which carry a regu- note will be an account of some of the lar icosahedron or dodecahedron onto itself (the Tmajor results over the past hundred unique simple group of order 60). This manifold years which have paved the way towards a proof has the homology of the 3-sphere, but its funda- and towards the even more ambitious project of mental group π1(SO(3)/I60) is a perfect group of classifying all compact 3-dimensional manifolds. order 120. He concluded the discussion by asking, The final paragraph provides a brief description of again translated into modern language: the latest developments, due to Grigory Perelman. A more serious discussion of Perelman’s work If a closed 3-dimensional manifold has will be provided in a subsequent note by Michael trivial fundamental group, must it be Anderson. homeomorphic to the 3-sphere? The conjecture that this is indeed the case has Poincaré’s Question come to be known as the Poincaré Conjecture. It At the very beginning of the twentieth century, has turned out to be an extraordinarily difficult Henri Poincaré (1854–1912) made an unwise claim, question, much harder than the corresponding which can be stated in modern language as follows: question in dimension five or more,2 and is a If a closed 3-dimensional manifold has key stumbling block in the effort to classify the homology of the sphere S3 , then it 3-dimensional manifolds. -

The Process of Student Cognition in Constructing Mathematical Conjecture
ISSN 2087-8885 E-ISSN 2407-0610 Journal on Mathematics Education Volume 9, No. 1, January 2018, pp. 15-26 THE PROCESS OF STUDENT COGNITION IN CONSTRUCTING MATHEMATICAL CONJECTURE I Wayan Puja Astawa1, I Ketut Budayasa2, Dwi Juniati2 1Ganesha University of Education, Jalan Udayana 11, Singaraja, Indonesia 2State University of Surabaya, Ketintang, Surabaya, Indonesia Email: [email protected] Abstract This research aims to describe the process of student cognition in constructing mathematical conjecture. Many researchers have studied this process but without giving a detailed explanation of how students understand the information to construct a mathematical conjecture. The researchers focus their analysis on how to construct and prove the conjecture. This article discusses the process of student cognition in constructing mathematical conjecture from the very beginning of the process. The process is studied through qualitative research involving six students from the Mathematics Education Department in the Ganesha University of Education. The process of student cognition in constructing mathematical conjecture is grouped into five different stages. The stages consist of understanding the problem, exploring the problem, formulating conjecture, justifying conjecture, and proving conjecture. In addition, details of the process of the students’ cognition in each stage are also discussed. Keywords: Process of Student Cognition, Mathematical Conjecture, qualitative research Abstrak Penelitian ini bertujuan untuk mendeskripsikan proses kognisi mahasiswa dalam mengonstruksi konjektur matematika. Beberapa peneliti mengkaji proses-proses ini tanpa menjelaskan bagaimana siswa memahami informasi untuk mengonstruksi konjektur. Para peneliti dalam analisisnya menekankan bagaimana mengonstruksi dan membuktikan konjektur. Artikel ini membahas proses kognisi mahasiswa dalam mengonstruksi konjektur matematika dari tahap paling awal. -

History of Mathematics
History of Mathematics James Tattersall, Providence College (Chair) Janet Beery, University of Redlands Robert E. Bradley, Adelphi University V. Frederick Rickey, United States Military Academy Lawrence Shirley, Towson University Introduction. There are many excellent reasons to study the history of mathematics. It helps students develop a deeper understanding of the mathematics they have already studied by seeing how it was developed over time and in various places. It encourages creative and flexible thinking by allowing students to see historical evidence that there are different and perfectly valid ways to view concepts and to carry out computations. Ideally, a History of Mathematics course should be a part of every mathematics major program. A course taught at the sophomore-level allows mathematics students to see the great wealth of mathematics that lies before them and encourages them to continue studying the subject. A one- or two-semester course taught at the senior level can dig deeper into the history of mathematics, incorporating many ideas from the 19th and 20th centuries that could only be approached with difficulty by less prepared students. Such a senior-level course might be a capstone experience taught in a seminar format. It would be wonderful for students, especially those planning to become middle school or high school mathematics teachers, to have the opportunity to take advantage of both options. We also encourage History of Mathematics courses taught to entering students interested in mathematics, perhaps as First Year or Honors Seminars; to general education students at any level; and to junior and senior mathematics majors and minors. Ideally, mathematics history would be incorporated seamlessly into all courses in the undergraduate mathematics curriculum in addition to being addressed in a few courses of the type we have listed. -
![Arxiv:2102.04549V2 [Math.GT] 26 Jun 2021 Ieade Nih Notesrcueo -Aiod.Alteeconj Polyto These and Norm All Thurston to the 3-Manifolds](https://docslib.b-cdn.net/cover/5884/arxiv-2102-04549v2-math-gt-26-jun-2021-ieade-nih-notesrcueo-aiod-alteeconj-polyto-these-and-norm-all-thurston-to-the-3-manifolds-635884.webp)
Arxiv:2102.04549V2 [Math.GT] 26 Jun 2021 Ieade Nih Notesrcueo -Aiod.Alteeconj Polyto These and Norm All Thurston to the 3-Manifolds
SURVEY ON L2-INVARIANTS AND 3-MANIFOLDS LUCK,¨ W. Abstract. In this paper give a survey about L2-invariants focusing on 3- manifolds. 0. Introduction The theory of L2-invariants was triggered by Atiyah in his paper on the L2-index theorem [4]. He followed the general principle to consider a classical invariant of a compact manifold and to define its analog for the universal covering taking the action of the fundamental group into account. Its application to (co)homology, Betti numbers and Reidemeister torsion led to the notions of L2-(cohomology), L2-Betti numbers and L2-torsion. Since then L2-invariants were developed much further. They already had and will continue to have striking, surprizing, and deep impact on questions and problems of fields, for some of which one would not expect any relation, e.g., to algebra, differential geometry, global analysis, group theory, topology, transformation groups, and von Neumann algebras. The theory of 3-manifolds has also a quite impressive history culminating in the work of Waldhausen and in particular of Thurston and much later in the proof of the Geometrization Conjecture by Perelman and of the Virtual Fibration Conjecture by Agol. It is amazing how many beautiful, easy to comprehend, and deep theorems, which often represent the best result one can hope for, have been proved for 3- manifolds. The motivating question of this survey paper is: What happens if these two prominent and successful areas meet one another? The answer will be: Something very interesting. In Section 1 we give a brief overview over basics about 3-manifolds, which of course can be skipped by someone who has already some background. -

THE MILLENIUM PROBLEMS the Seven Greatest Unsolved Mathematifcal Puzzles of Our Time Freshman Seminar University of California, Irvine
THE MILLENIUM PROBLEMS The Seven Greatest Unsolved Mathematifcal Puzzles of our Time Freshman Seminar University of California, Irvine Bernard Russo University of California, Irvine Fall 2014 Bernard Russo (UCI) THE MILLENIUM PROBLEMS The Seven Greatest Unsolved Mathematifcal Puzzles of our Time 1 / 11 Preface In May 2000, at a highly publicized meeting in Paris, the Clay Mathematics Institute announced that seven $1 million prizes were being offered for the solutions to each of seven unsolved problems of mathematics |problems that an international committee of mathematicians had judged to be the seven most difficult and most important in the field today. For some of these problems, it takes considerable effort simply to understand the individual terms that appear in the statement of the problem. It is not possible to describe most of them accurately in lay terms|or even in terms familiar to someone with a university degree in mathematics. The goal of this seminar is to provide the background to each problem, to describe how it arose, explain what makes it particularly difficult, and give some sense of why mathematicians regard it as important. This seminar is not for those who want to tackle one of the problems, but rather for mathematicians and non-mathematicians alike who are curious about the current state at the frontiers of humankind's oldest body of scientific knowledge. Bernard Russo (UCI) THE MILLENIUM PROBLEMS The Seven Greatest Unsolved Mathematifcal Puzzles of our Time 2 / 11 After three thousand years of intellectual development, what are the limits of our mathematical knowledge? To benefit from this seminar, all you need by way of background is a good high school knowledge of mathematics. -
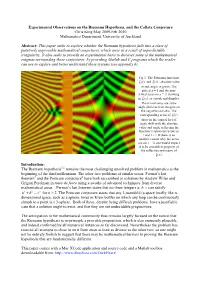
Experimental Observations on the Riemann Hypothesis, and the Collatz Conjecture Chris King May 2009-Feb 2010 Mathematics Department, University of Auckland
Experimental Observations on the Riemann Hypothesis, and the Collatz Conjecture Chris King May 2009-Feb 2010 Mathematics Department, University of Auckland Abstract: This paper seeks to explore whether the Riemann hypothesis falls into a class of putatively unprovable mathematical conjectures, which arise as a result of unpredictable irregularity. It also seeks to provide an experimental basis to discover some of the mathematical enigmas surrounding these conjectures, by providing Matlab and C programs which the reader can use to explore and better understand these systems (see appendix 6). Fig 1: The Riemann functions (z) and (z) : absolute value in red, angle in green. The pole at z = 1 and the non- trivial zeros on x = showing in (z) as a peak and dimples. The trivial zeros are at the angle shifts at even integers on the negative real axis. The corresponding zeros of (z) show in the central foci of angle shift with the absolute value and angle reflecting the function’s symmetry between z and 1 - z. If there is an analytic reason why the zeros are on x = one would expect it to be a manifest property of the reflective symmetry of (z) . Introduction: The Riemann hypothesis1,2 remains the most challenging unsolved problem in mathematics at the beginning of the third millennium. The other two problems of similar status, Fermat’s last theorem3 and the Poincare conjecture4 have both succumbed to solutions by Andrew Wiles and Grigori Perelman in tours de force using a swathe of advanced techniques from diverse mathematical areas. Fermat’s last theorem states that no three integers a, b, c can satisfy an + bn = cn for n > 2. -

The Role of the Ramanujan Conjecture in Analytic Number Theory
BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY Volume 50, Number 2, April 2013, Pages 267–320 S 0273-0979(2013)01404-6 Article electronically published on January 14, 2013 THE ROLE OF THE RAMANUJAN CONJECTURE IN ANALYTIC NUMBER THEORY VALENTIN BLOMER AND FARRELL BRUMLEY Dedicated to the 125th birthday of Srinivasa Ramanujan Abstract. We discuss progress towards the Ramanujan conjecture for the group GLn and its relation to various other topics in analytic number theory. Contents 1. Introduction 267 2. Background on Maaß forms 270 3. The Ramanujan conjecture for Maaß forms 276 4. The Ramanujan conjecture for GLn 283 5. Numerical improvements towards the Ramanujan conjecture and applications 290 6. L-functions 294 7. Techniques over Q 298 8. Techniques over number fields 302 9. Perspectives 305 J.-P. Serre’s 1981 letter to J.-M. Deshouillers 307 Acknowledgments 313 About the authors 313 References 313 1. Introduction In a remarkable article [111], published in 1916, Ramanujan considered the func- tion ∞ ∞ Δ(z)=(2π)12e2πiz (1 − e2πinz)24 =(2π)12 τ(n)e2πinz, n=1 n=1 where z ∈ H = {z ∈ C |z>0} is in the upper half-plane. The right hand side is understood as a definition for the arithmetic function τ(n) that nowadays bears Received by the editors June 8, 2012. 2010 Mathematics Subject Classification. Primary 11F70. Key words and phrases. Ramanujan conjecture, L-functions, number fields, non-vanishing, functoriality. The first author was supported by the Volkswagen Foundation and a Starting Grant of the European Research Council. The second author is partially supported by the ANR grant ArShiFo ANR-BLANC-114-2010 and by the Advanced Research Grant 228304 from the European Research Council. -

The Poincaré Conjecture and Poincaré's Prize
Book Review The Poincaré Conjecture and Poincaré’s Prize Reviewed by W. B. Raymond Lickorish can be shrunk to a point. Armed with a gradu- The Poincaré Conjecture: In Search of the Shape ate course in topology, and perhaps also aware of the Universe that any three-manifold can both be triangulated Donal O’Shea Walker, March 2007 and given a differential structure, an adventurer 304 pages, US$15.95, ISBN 978-0802706545 could set out to find fame and fortune by con- quering the Poincaré Conjecture. Gradually the Poincaré’s Prize: The Hundred-Year Quest to conjecture acquired a draconian reputation: many Solve One of Math’s Greatest Puzzles were its victims. Early attempts at the conjec- George G. Szpiro ture produced some interesting incidental results: Dutton, June 2007 Poincaré himself, when grappling with the proper 320 pages, US$24.95, ISBN 978-0525950240 statement of the problem, discovered his dodec- ahedral homology three-sphere that is not S3; J. H. C. Whitehead, some thirty years later, dis- Here are two books that, placing their narratives carded his own erroneous solution on discovering in abundant historical context and avoiding all a contractible (all homotopy groups trivial) three- symbols and formulae, tell of the triumph of Grig- manifold not homeomorphic to R3. However, for ory Perelman. He, by developing ideas of Richard the last half-century, the conjecture has too often Hamilton concerning curvature, has given an affir- enticed devotees into a fruitless addiction with mative solution to the famous problem known as regrettable consequences. the Poincaré Conjecture. This conjecture, posed The allure of the Poincaré Conjecture has cer- as a question by Henri Poincaré in 1904, was tainly provided an underlying motivation for much a fundamental question about three-dimensional research in three-manifolds. -

Marden's Tameness Conjecture
MARDEN'S TAMENESS CONJECTURE: HISTORY AND APPLICATIONS RICHARD D. CANARY Abstract. Marden's Tameness Conjecture predicts that every hyperbolic 3-manifold with finitely generated fundamental group is homeomorphic to the interior of a compact 3-manifold. It was recently established by Agol and Calegari-Gabai. We will survey the history of work on this conjecture and discuss its many appli- cations. 1. Introduction In a seminal paper, published in the Annals of Mathematics in 1974, Al Marden [65] conjectured that every hyperbolic 3-manifold with finitely generated fundamental group is homeomorphic to the interior of a compact 3-manifold. This conjecture evolved into one of the central conjectures in the theory of hyperbolic 3-manifolds. For example, Mar- den's Tameness Conjecture implies Ahlfors' Measure Conjecture (which we will discuss later). It is a crucial piece in the recently completed classification of hyperbolic 3-manifolds with finitely generated funda- mental group. It also has important applications to geometry and dy- namics of hyperbolic 3-manifolds and gives important group-theoretic information about fundamental groups of hyperbolic 3-manifolds. There is a long history of partial results in the direction of Marden's Tameness Conjecture and it was recently completely established by Agol [1] and Calegari-Gabai [27]. In this brief expository paper, we will survey the history of these results and discuss some of the most important applications. Outline of paper: In section 2, we recall basic definitions from the theory of hyperbolic 3-manifolds. In section 3, we construct a 3- manifold with finitely generated fundamental group which is not home- omorphic to the interior of a compact 3-manifold. -

Die Hauptvermutung Der Kombinatorischen Topologie
Abel Prize Laureate 2011 John Willard Milnor Die Hauptvermutung der kombinatorischen Topolo- gie (Steiniz, Tietze; 1908) Die Hauptvermutung (The main Conjecture) of combinatorial topology (now: algebraic topology) was published in 1908 by the German mathematician Ernst Steiniz and the Austrian mathematician Heinrich Tietze. The conjecture states that given two trian- gulations of the same space, there is always possible to find a common refinement. The conjecture was proved in dimension 2 by Tibor Radó in the 1920s and in dimension 3 by Edwin E. Moise in the 1950s. The conjecture was disproved in dimension greater or equal to 6 by John Milnor in 1961. Triangulation by points. Next you chose a bunch of connecting “Norges Geografiske Oppmåling” (NGO) was lines, edges, between the reference points in order established in 1773 by the military officer Hein- to obtain a tiangular web. The choices of refer- rich Wilhelm von Huth with the purpose of meas- ence points and edges are done in order to ob- uring Norway in order to draw precise and use- tain triangles where the curvature of the interior ful maps. Six years later they started the rather landscape is neglectable. Thus, if the landscape is elaborate triangulation task. When triangulating hilly, the reference points have to be chosen rath- a piece of land you have to pick reference points er dense, while flat farmland doesn´t need many and compute their coordinates relative to near- points. In this way it is possible to give a rather accurate description of the whole landscape. The recipe of triangulation can be used for arbitrary surfaces.