DOCSLIB.ORG

Bremsstrahlung –”Braking Radiation”

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bremsstrahlung –”Braking Radiation” Bremsstrahlung –”braking radiation” Consider essentially the reverse process of the photoelectric effect, the impact of high- energy electrons (KE~10 keV) on a surface (or another particle) Since the electrons rapidly decelerate, one expects the production of EM radiation Classically, the radiation frequency should cover the entire spectrum, i.e. all frequencies Experimentally, a maximum frequency fmax (or minimum wavelength lmin ) is observed For very short wavelengths (l~0.01-10 Å), we need to treat EM radiation like a particle, i.e. photons So, consider the same conservation of energy relation as used for the photoelectric effect However, KE=10 keV>> f (the work function), so we can neglect f ®®®® KEbefore = hf + KEafter Maximum photon frequency occurs for KE =0 ®®® KEbefore after fmax = All electron KE is converted h to photon energy (x-ray) hc l = Further evidence of particle min KE behavior of EM radiation before Compton Scattering Scattering of EM radiation (x-rays) off of a “free” electron Classically, if the radiation is treated as a wave one expects the following: - radiative “pressure” should slowly cause the electron to accelerate in the direction of the wave propagation - the electrons would aBsorb the radiation of frequency f and reradiate (scattering), But in all directions. However, a Doppler shift would slowly develop as the electron accelerated. The emitted frequency f’ would Be shifted. ØSince the electron should absorb different amounts of energy (since it is accelerating, and the electron sees the EM wave slowly being redshifted), a broad distribution of Doppler-shifted frequencies was expected ØThis was not observed! ØIn 1932, Compton found that for a given detector angle q, only one frequency f’ (l’) was observed ®® ØAgain, the classical wave picture fails when considering EM radiation of very short wavelength ØThe quantum particle picture is then adopted to explain this effect as an elastic collision. Apply - conservation of energy - conservation of momentum! ØThe change in wavelength is found to be h l'-l = Dl = (1- cosq ) mec ØDl depends only on the scattered photon angle ØIndependent of time; contrary to classical expectations Øl’>l, since photon loses energy, electron gains KE ØWhen q=180°, Dl is maximum; called back scattering 2h Dlmax = mec ØCompton’s experiment was the first proof of the photon’s momentum ØAgain, the particle interpretation of radiation is required As mentioned, Compton scattering on an electron is an elastic process since the electron’s mass cannot change However, inelastic Compton scattering can occur on composite particles, i.e. a nucleus, whose mass (internal energy) can change. Conservation of total energy still holds. Inelastic Compton scattering is not relevant to atoms. It would involve the removal of an electron, but the electron binding energy (~10 eV, also called the ionization potential) is much less than the energy of an x-ray Finally, the predictions of classical wave theory are valid if the wavelength is large, or f small Pair Production For photon collisions we have seen that it is possible for the photon to give up all of its energy (photoelectric effect; visible or ultraviolet) or some of its energy (Compton effect; x-ray) If the photon is a gamma ray (g-ray; l <0.01 Å or E> 1 MeV), it can spontaneously give up all of its energy to produce a particle – antiparticle pair The process, however, cannot occur in a vacuum, but results from an electromagnetic interaction when the g-ray passes near an atomic nucleus Without the atomic nucleus, momentum conservation is violated. The extra particle is needed to remove extra momentum Bubble chamber with magnetic field pointing out of the figure A general rule: all reactions require at least two reactants and two products so that momentum is conserved The heavier of the two particles will always have a smaller change in KE For pair production, the photon again must be treated as a particle!.
Load more

Recommended publications
  • Compton Scattering from the Deuteron at Low Energies
    SE0200264 LUNFD6-NFFR-1018 Compton Scattering from the Deuteron at Low Energies Magnus Lundin Department of Physics Lund University 2002 W' •sii" Compton spridning från deuteronen vid låga energier (populärvetenskaplig sammanfattning på svenska) Vid Compton spridning sprids fotonen elastiskt, dvs. utan att förlora energi, mot en annan partikel eller kärna. Kärnorna som användes i detta försök består av en proton och en neutron (sk. deuterium, eller tungt väte). Kärnorna bestrålades med fotoner av kända energier och de spridda fo- tonerna detekterades mha. stora Nal-detektorer som var placerade i olika vinklar runt strålmålet. Försöket utfördes under 8 veckor och genom att räkna antalet fotoner som kärnorna bestålades med och antalet spridda fo- toner i de olika detektorerna, kan sannolikheten för att en foton skall spridas bestämmas. Denna sannolikhet jämfördes med en teoretisk modell som beskriver sannolikheten för att en foton skall spridas elastiskt mot en deuterium- kärna. Eftersom protonen och neutronen består av kvarkar, vilka har en elektrisk laddning, kommer dessa att sträckas ut då de utsätts för ett elek- triskt fält (fotonen), dvs. de polariseras. Värdet (sannolikheten) som den teoretiska modellen ger, beror på polariserbarheten hos protonen och neu- tronen i deuterium. Genom att beräkna sannolikheten för fotonspridning för olika värden av polariserbarheterna, kan man se vilket värde som ger bäst överensstämmelse mellan modellen och experimentella data. Det är speciellt neutronens polariserbarhet som är av intresse, och denna kunde bestämmas i detta arbete. Organization Document name LUND UNIVERSITY DOCTORAL DISSERTATION Department of Physics Date of issue 2002.04.29 Division of Nuclear Physics Box 118 Sponsoring organization SE-22100 Lund Sweden Author (s) Magnus Lundin Title and subtitle Compton Scattering from the Deuteron at Low Energies Abstract A series of three Compton scattering experiments on deuterium have been performed at the high-resolution tagged-photon facility MAX-lab located in Lund, Sweden.
    [Show full text]
  • 7. Gamma and X-Ray Interactions in Matter
    Photon interactions in matter Gamma- and X-Ray • Compton effect • Photoelectric effect Interactions in Matter • Pair production • Rayleigh (coherent) scattering Chapter 7 • Photonuclear interactions F.A. Attix, Introduction to Radiological Kinematics Physics and Radiation Dosimetry Interaction cross sections Energy-transfer cross sections Mass attenuation coefficients 1 2 Compton interaction A.H. Compton • Inelastic photon scattering by an electron • Arthur Holly Compton (September 10, 1892 – March 15, 1962) • Main assumption: the electron struck by the • Received Nobel prize in physics 1927 for incoming photon is unbound and stationary his discovery of the Compton effect – The largest contribution from binding is under • Was a key figure in the Manhattan Project, condition of high Z, low energy and creation of first nuclear reactor, which went critical in December 1942 – Under these conditions photoelectric effect is dominant Born and buried in • Consider two aspects: kinematics and cross Wooster, OH http://en.wikipedia.org/wiki/Arthur_Compton sections http://www.findagrave.com/cgi-bin/fg.cgi?page=gr&GRid=22551 3 4 Compton interaction: Kinematics Compton interaction: Kinematics • An earlier theory of -ray scattering by Thomson, based on observations only at low energies, predicted that the scattered photon should always have the same energy as the incident one, regardless of h or • The failure of the Thomson theory to describe high-energy photon scattering necessitated the • Inelastic collision • After the collision the electron departs
    [Show full text]
  • Arxiv:2104.05705V3 [Gr-Qc] 11 May 2021
    Bremsstrahlung of Light through Spontaneous Emission of Gravitational Waves Charles H.-T. Wang and Melania Mieczkowska Department of Physics, University of Aberdeen, King's College, Aberdeen AB24 3UE, United Kingdom 11 May 2021 Published in the Special Issue of Symmetry: New Frontiers in Quantum Gravity Abstract Zero-point fluctuations are a universal consequence of quantum theory. Vacuum fluctuations of electro- magnetic field have provided crucial evidence and guidance for QED as a successful quantum field theory with a defining gauge symmetry through the Lamb shift, Casimir effect, and spontaneous emission. In an accelerated frame, the thermalisation of the zero-point electromagnetic field gives rise to the Unruh effect linked to the Hawking effect of a black hole via the equivalence principle. This principle is the basis of general covariance, the symmetry of general relativity as the classical theory of gravity. If quantum gravity exists, the quantum vacuum fluctuations of the gravitational field should also lead to the quantum deco- herence and dissertation of general forms of energy and matter. Here we present a novel theoretical effect involving the spontaneous emission of soft gravitons by photons as they bend around a heavy mass and dis- cuss its observational prospects. Our analytic and numerical investigations suggest that the gravitational bending of starlight predicted by classical general relativity should also be accompanied by the emission of gravitational waves. This in turn redshifts the light causing a loss of its energy somewhat analogous to the bremsstrahlung of electrons by a heavier charged particle. It is suggested that this new effect may be important for a combined astronomical source of intense gravity and high-frequency radiation such as X-ray binaries and that the proposed LISA mission may be potentially sensitive to the resulting sub-Hz stochastic gravitational waves.
    [Show full text]
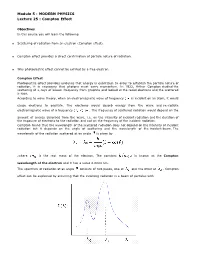
  • Compton Effect
    Module 5 : MODERN PHYSICS Lecture 25 : Compton Effect Objectives In this course you will learn the following Scattering of radiation from an electron (Compton effect). Compton effect provides a direct confirmation of particle nature of radiation. Why photoelectric effect cannot be exhited by a free electron. Compton Effect Photoelectric effect provides evidence that energy is quantized. In order to establish the particle nature of radiation, it is necessary that photons must carry momentum. In 1922, Arthur Compton studied the scattering of x-rays of known frequency from graphite and looked at the recoil electrons and the scattered x-rays. According to wave theory, when an electromagnetic wave of frequency is incident on an atom, it would cause electrons to oscillate. The electrons would absorb energy from the wave and re-radiate electromagnetic wave of a frequency . The frequency of scattered radiation would depend on the amount of energy absorbed from the wave, i.e. on the intensity of incident radiation and the duration of the exposure of electrons to the radiation and not on the frequency of the incident radiation. Compton found that the wavelength of the scattered radiation does not depend on the intensity of incident radiation but it depends on the angle of scattering and the wavelength of the incident beam. The wavelength of the radiation scattered at an angle is given by .where is the rest mass of the electron. The constant is known as the Compton wavelength of the electron and it has a value 0.0024 nm. The spectrum of radiation at an angle consists of two peaks, one at and the other at .
    [Show full text]
  • Dose Measurements of Bremsstrahlung-Produced Neutrons at the Advanced Photon Source
    ANL/APS/LS-269 Dose Measurements of Bremsstrahlung-Produced Neutrons at the Advanced Photon Source by M. Pisharody, E. Semones, and P. K. Job August 1998 Advanced Photon Source Argonne National Laboratory operated by The University of Chicago for the US Department of Energy under Contract W-31-I09-Eng-38 Argonne National Laboratory, with facilities in the states of Illinois and Idaho, is owned by the United States government, and operated by The University of Chicago under the provisions of a contract with the Department of Energy. DISCLAIMER- This report was prepared as an account of work sponsored by an agency of the United States Government Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or pro- cess disclosed, or represents that its use would not infringe privately owned rights Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not necessanly constitute or imply its endorsement, recommendation or favoring by the United States Government or any agency thereof The views and opinions of authors expressed herein do not necessanly state or reflect those of the United States Government or any agency thereof. Reproduced from the best available copy Available to DOE and DOE contractors from the Office of Scientific and Technical Information P.O. Box 62 Oak Ridge, TN 37831 Prices available from (4231 576-8401 Available to the public from the National Technical Information Service U.S.
    [Show full text]
  • Compton Scattering from Low to High Energies
    Compton Scattering from Low to High Energies Marc Vanderhaeghen College of William & Mary / JLab HUGS 2004 @ JLab, June 1-18 2004 Outline Lecture 1 : Real Compton scattering on the nucleon and sum rules Lecture 2 : Forward virtual Compton scattering & nucleon structure functions Lecture 3 : Deeply virtual Compton scattering & generalized parton distributions Lecture 4 : Two-photon exchange physics in elastic electron-nucleon scattering …if you want to read more details in preparing these lectures, I have primarily used some review papers : Lecture 1, 2 : Drechsel, Pasquini, Vdh : Physics Reports 378 (2003) 99 - 205 Lecture 3 : Guichon, Vdh : Prog. Part. Nucl. Phys. 41 (1998) 125 – 190 Goeke, Polyakov, Vdh : Prog. Part. Nucl. Phys. 47 (2001) 401 - 515 Lecture 4 : research papers , field in rapid development since 2002 1st lecture : Real Compton scattering on the nucleon & sum rules IntroductionIntroduction :: thethe realreal ComptonCompton scatteringscattering (RCS)(RCS) processprocess ε, ε’ : photon polarization vectors σ, σ’ : nucleon spin projections Kinematics in LAB system : shift in wavelength of scattered photon Compton (1923) ComptonCompton scatteringscattering onon pointpoint particlesparticles Compton scattering on spin 1/2 point particle (Dirac) e.g. e- Klein-Nishina (1929) : Thomson term ΘL = 0 Compton scattering on spin 1/2 particle with anomalous magnetic moment Stern (1933) Powell (1949) LowLow energyenergy expansionexpansion ofof RCSRCS processprocess Spin-independent RCS amplitude note : transverse photons : Low
    [Show full text]
  • The Basic Interactions Between Photons and Charged Particles With
    Outline Chapter 6 The Basic Interactions between • Photon interactions Photons and Charged Particles – Photoelectric effect – Compton scattering with Matter – Pair productions Radiation Dosimetry I – Coherent scattering • Charged particle interactions – Stopping power and range Text: H.E Johns and J.R. Cunningham, The – Bremsstrahlung interaction th physics of radiology, 4 ed. – Bragg peak http://www.utoledo.edu/med/depts/radther Photon interactions Photoelectric effect • Collision between a photon and an • With energy deposition atom results in ejection of a bound – Photoelectric effect electron – Compton scattering • The photon disappears and is replaced by an electron ejected from the atom • No energy deposition in classical Thomson treatment with kinetic energy KE = hν − Eb – Pair production (above the threshold of 1.02 MeV) • Highest probability if the photon – Photo-nuclear interactions for higher energies energy is just above the binding energy (above 10 MeV) of the electron (absorption edge) • Additional energy may be deposited • Without energy deposition locally by Auger electrons and/or – Coherent scattering Photoelectric mass attenuation coefficients fluorescence photons of lead and soft tissue as a function of photon energy. K and L-absorption edges are shown for lead Thomson scattering Photoelectric effect (classical treatment) • Electron tends to be ejected • Elastic scattering of photon (EM wave) on free electron o at 90 for low energy • Electron is accelerated by EM wave and radiates a wave photons, and approaching • No
    [Show full text]
  • Quantum Electric Field Fluctuations and Potential Scattering
    Quantum Electric Field Fluctuations and Potential Scattering Haiyun Huang1, ∗ and L. H. Ford1, y 1Institute of Cosmology, Department of Physics and Astronomy Tufts University, Medford, Massachusetts 02155, USA Abstract Some physical effects of time averaged quantum electric field fluctuations are discussed. The one loop radiative correction to potential scattering are approximately derived from simple arguments which invoke vacuum electric field fluctuations. For both above barrier scattering and quantum tunneling, this effect increases the transmission probability. It is argued that the shape of the potential determines a sampling function for the time averaging of the quantum electric field oper- ator. We also suggest that there is a nonperturbative enhancement of the transmission probability which can be inferred from the probability distribution for time averaged electric field fluctuations. PACS numbers: 03.70.+k, 12.20.Ds, 05.40.-a arXiv:1503.02962v1 [hep-th] 10 Mar 2015 ∗Electronic address: [email protected] yElectronic address: [email protected] 1 I. INTRODUCTION The vacuum fluctuations of the quantized electromagnetic field give rise a number of physical effects, including the Casimir effect, the Lamb shift, and the anomalous magnetic moment of the electron. Many of these effects are calculated in perturbative quantum electrodynamics, often by a procedure which does not easily lend itself to an interpretation in terms of field fluctuations. An exception is Welton's [1] calculation of the dominant contribution to the Lamb shift, which leads to a simple physical picture in which electric field fluctuations cause an electron in the 2s state of hydrogen to be shifted upwards in energy.
    [Show full text]
  • Interactions of Photons with Matter
    22.55 “Principles of Radiation Interactions” Interactions of Photons with Matter • Photons are electromagnetic radiation with zero mass, zero charge, and a velocity that is always c, the speed of light. • Because they are electrically neutral, they do not steadily lose energy via coulombic interactions with atomic electrons, as do charged particles. • Photons travel some considerable distance before undergoing a more “catastrophic” interaction leading to partial or total transfer of the photon energy to electron energy. • These electrons will ultimately deposit their energy in the medium. • Photons are far more penetrating than charged particles of similar energy. Energy Loss Mechanisms • photoelectric effect • Compton scattering • pair production Interaction probability • linear attenuation coefficient, µ, The probability of an interaction per unit distance traveled Dimensions of inverse length (eg. cm-1). −µ x N = N0 e • The coefficient µ depends on photon energy and on the material being traversed. µ • mass attenuation coefficient, ρ The probability of an interaction per g cm-2 of material traversed. Units of cm2 g-1 ⎛ µ ⎞ −⎜ ⎟()ρ x ⎝ ρ ⎠ N = N0 e Radiation Interactions: photons Page 1 of 13 22.55 “Principles of Radiation Interactions” Mechanisms of Energy Loss: Photoelectric Effect • In the photoelectric absorption process, a photon undergoes an interaction with an absorber atom in which the photon completely disappears. • In its place, an energetic photoelectron is ejected from one of the bound shells of the atom. • For gamma rays of sufficient energy, the most probable origin of the photoelectron is the most tightly bound or K shell of the atom. • The photoelectron appears with an energy given by Ee- = hv – Eb (Eb represents the binding energy of the photoelectron in its original shell) Thus for gamma-ray energies of more than a few hundred keV, the photoelectron carries off the majority of the original photon energy.
    [Show full text]
  • Bremsstrahlung in Α Decay Reexamined
    Missouri University of Science and Technology Scholars' Mine Physics Faculty Research & Creative Works Physics 01 Jul 2007 Bremsstrahlung in α decay reexamined H. Boie Heiko Scheit Ulrich D. Jentschura Missouri University of Science and Technology, [email protected] F. Kock et. al. For a complete list of authors, see https://scholarsmine.mst.edu/phys_facwork/838 Follow this and additional works at: https://scholarsmine.mst.edu/phys_facwork Part of the Physics Commons Recommended Citation H. Boie et al., "Bremsstrahlung in α decay reexamined," Physical Review Letters, vol. 99, no. 2, pp. 022505-1-022505-4, American Physical Society (APS), Jul 2007. The definitive version is available at https://doi.org/10.1103/PhysRevLett.99.022505 This Article - Journal is brought to you for free and open access by Scholars' Mine. It has been accepted for inclusion in Physics Faculty Research & Creative Works by an authorized administrator of Scholars' Mine. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. PHYSICAL REVIEW LETTERS week ending PRL 99, 022505 (2007) 13 JULY 2007 Bremsstrahlung in Decay Reexamined H. Boie,1 H. Scheit,1 U. D. Jentschura,1 F. Ko¨ck,1 M. Lauer,1 A. I. Milstein,2 I. S. Terekhov,2 and D. Schwalm1,* 1Max-Planck-Institut fu¨r Kernphysik, D-69117 Heidelberg, Germany 2Budker Institute of Nuclear Physics, 630090 Novosibirsk, Russia (Received 29 March 2007; published 13 July 2007) A high-statistics measurement of bremsstrahlung emitted in the decay of 210Po has been performed, which allows us to follow the photon spectra up to energies of 500 keV.
    [Show full text]
  • Fundamental Study of Compton Scattering Tomography
    FUNDAMENTAL STUDY OF COMPTON SCATTERING TOMOGRAPHY R. XIAO, S. SATO, C. UYAMAf, and T. NAKAMURAJ Department of Biophysical Engineering, Faculty of Engineering Science, Osaka University \ Department of Investigative Radiology, National Cardiovascular Center Research Institute \Cyclotron and Radioisotope Center, Tohoku University 1. Introduction Compton scattering tomography is an imaging technique that forms tomographic im­ ages corresponding to distribution of electron densities in an X-rays or 7-rays1 irradiating object by measuring Compton scattered photons emitted out of it. Because of its advan­ tage of free choice of measurement geometry, Compton scattering tomography is useful for inspection of defects inside huge objects in industry where X-rays or 7-rays can hardly pen­ etrate the objects[l]. For medical usage, Compton scattered rays are used for densitometry of bone or other tissues. Compton scattering tomographic images, in which densities of body other than attenuation coefficients of body can be shown, are meaningful for medical diagnoses. Before building a real Compton scattering tomography system for medical applica­ tions, we made some fundamental observations upon Compton scattering imaging process through Monte Carlo simulation in order to testify feasibility of the imaging and to seek for an available scheme of system design. EGS4 code system[2] is used for simulation of transport processes of photons in an imaged object. Multiple scattering, one of factors that influence quantity of Compton scattering images, is evaluated here. Some methods to overcome multiple scattering are proposed and their effects are discussed below. 2. Principle of Compton scattering tomography A beam of X-rays or 7-rays attenuates in its intensity by interactions of photoelectric absorption, Compton scattering, Rayleigh scattering and electron-positron pair production while it is passing through an object.
    [Show full text]
  • Lecture 18 Quantum Electrodynamics
    Lecture 18 Quantum Electrodynamics Quantum Electrodynamics (QED) describes a U(1) gauge theory coupled to a fermion, e.g. the electron, muon or any other charged particle. As we saw previously the lagrangian for such theory is 1 L = ¯(iD6 − m) − F F µν ; (18.1) 4 µν where the covariant derivative is defined as Dµ (x) = (@µ + ieAµ(x)) (x) ; (18.2) resulting in 1 L = ¯(i6@ − m) − F F µν − eA ¯γµ ; (18.3) 4 µν µ where the last term is the interaction lagrangian and thus e is the photon-fermion cou- pling. We would like to derive the Feynman rules for this theory, and then compute the amplitudes and cross sections for some interesting processes. 18.1 Feynman Rules for QED In addition to the rules for the photon and fermion propagator, we now need to derive the Feynman rule for the photon-fermion vertex. One way of doing this is to use the generating functional in presence of linearly coupled external sources Z ¯ R 4 µ ¯ ¯ iS[ ; ;Aµ]+i d xfJµA +¯η + ηg Z[η; η;¯ Jµ] = N D D DAµ e : (18.4) 1 2 LECTURE 18. QUANTUM ELECTRODYNAMICS From it we can derive a three-point function with an external photon, a fermion and an antifermion. This is given by 3 3 (3) (−i) δ Z[η; η;¯ Jµ] G (x1; x2; x3) = ; (18.5) Z[0; 0; 0] δJ (x )δη(x )δη¯(x ) µ 1 2 3 Jµ,η;η¯=0 which, when we expand in the interaction term, results in 1 Z ¯ G(3)(x ; x ; x ) = D ¯ D DA eiS0[ ; ;Aµ]A (x ) ¯(x ) (x ) 1 2 3 Z[0; 0; 0] µ µ 1 2 3 Z 4 ¯ ν × 1 − ie d yAν(y) (y)γ (y) + ::: Z 4 ν = (+ie) d yDF µν(x1 − y)Tr [SF(x3 − y)γ SF(x2 − y)] ; (18.6) where S0 is the free action, obtained from the first two terms in (18.3).
    [Show full text]