DOCSLIB.ORG

Option Strategies. Probability Distributions. Performance 1.1 Market Scenario Undecided

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Option Strategies. Probability Distributions. Performance 1.1 Market Scenario Undecided Option Strategies. Probability distributions. Performance 1.1 Market scenario undecided. Volatility undecided 1.1.1 Complete hedge using options The payoff of the underlying asset (long share) can be completely hedged by selling a call, buying a put option and selling a riskless bond. This combination would behave like selling the underlying security. 1.1.2 Box Spread Table 1. Box Spread. The Value Matrix S<E1 E1<S<E2 S>E2 Call -C1 -C1 + S - E1 -C1 + S - E1 - Call +C2 +C2 +C2 -( S - E2) Put -P2 + E2 - S -P2 + E2 - S - P2 - Put +P1 - (E1 - S) + P1 + P1 Total payoff -C + E2 - E1 -C + E2 - E1 -C + E2 - E1 Profit /Loss E2-E1 E2-E1-C1+C2+P1-P2 E1 E2 Spot Price (S) Figure 1. Box Spread Derivatives Market 231231-0345 1.2 Market scenario undecided. Volatility rising 1.2.1 Long Straddle Table 2. Long Straddle. The Value Matrix S<E S>E Call -C0 -C0 + S - E Put -P0 + E - S - P0 Total payoff + E - S - C0 - P0 + S - E -C0 - P0 Profit Break-even Point S=E-(P0+C0) /Loss -(P0+C0) Break-even Point S=E+P0+C0 E Spot Price (S) CF=-(P0+C0) Premiums Figure 2. Long Straddle 2 Derivatives Market 231231-0345 1.2.2 Long Strangle Table 3. Long Strangle. The Value Matrix S<E1 E1<S<E2 S>E2 Put (E1) -P1 + E1 - S -P1 - P1 Call (E2) -C2 - C2 - C2 + S - E2 Total payoff -P1 -C2 + E1 - S - P1 - C2 - P1- C2+ S - E2 Profit Break-even Point S=E1- (P1+C2) /Loss E1 E1-(P1+C2) Break-even Point S=E2+P1+C3 -(P1+C2) E1 E2 Spot Price (S) Figure 3. Long Strangle 3 Derivatives Market 231231-0345 1.2.3 Short Butterfly Spread Table 4. Short Butterfly Spread. The Value Matrix S<E1 E1<S<E2 E2<S<E3 S>E3 - Call (E1) C1 C1 - S + E1 C1 - S + E1 C1 - S + E1 - Call (E3) C3 C3 C3 C3 - S + E3 Call (E2) -2C2 -2C2 -2C2 + 2(S - E2) -2C2 + 2(S - E2) Total payoff -S + E1 S - 2E2 + E1 -2E2 + E1 + E3 -2C2 + C1 + C3 - 2C2 + C1 + C3 - 2C2 + C1 + C3 - 2C2 + C1 + C3 Profit Break-even Point S=E1+(C1+C3-2C2) /Loss Break-even Point S=E3-(C1+C3-2C2) -2C2+C1+C3 E1 E2 E3 Spot Price (S) E1-E2+C1+C3-2C2 Figure 4. Short Butterfly Spread 4 Derivatives Market 231231-0345 1.2.4 Short Condor Table 5. Short Condor. The Value Matrix S<E1 E1<S<E2 E2<S<E3 E3<S<E4 S>E4 - Call (E1) +C1 C1 - (S - E1) C1 - (S - E1) C1 - (S - E1) C1 - (S - E1) Call (E2) -C2 -C2 -C2 + S - E2 -C2 + S - E2 -C2 + S - E2 Call (E3) -C3 -C3 -C3 -C3 + S - E3 -C3 + S - E3 - Call (E4) C4 C4 C4 C4 C4 - (S - E4) Total payoff C -S + E1 + C -E2 + E1 + C -E3 -E2 +E1 +S -E3 -E2 +E1 +E4 +C +C Profit Break-even Point S=E2-C1-C4+C2+C3 /Loss Break-even Point S=E3+C1+C4-C2-C3 E2-E1 E2-E1+C1+C4-C2-C3 E1 E2 E3 E4 Spot Price (S) +C1+C4-C2-C3 Figure 5. Short Condor 5 Derivatives Market 231231-0345 1.3 Market scenario undecided. Volatility falling 1.3.1 Short Straddle Table 6. Short Straddle. The Value Matrix S<E S>E - Call +C0 +C0 - (S - E) - Put +P0 - (E - S) + P0 Total payoff S -E +C0 + P0 E - S +C0 + P0 Profit Break-even Point S=E-(P0+C0) /Loss Break-even Point S=E+P0+C0 (P0+C0) E Spot Price (S) (P0+C0) -E Figure 6. Short Straddle 6 Derivatives Market 231231-0345 1.3.2 Short Strangle Table 7. Short Strangle. The Value Matrix S<E1 E1<S<E2 S>E2 - Put (E1) P1 - E1 + S P1 P1 - Call (E2) C2 C2 C2 - S + E2 Total payoff P1 + C2 - E1 +S P1 + C2 P1 + C2 - S + E2 Profit Break-even Point S=E1- (P1+C2) /Loss Break-even Point P1+C2 S=E2+P1+C3 E1 E2 Spot Price (S) Figure 7. Short Strangle 7 Derivatives Market 231231-0345 1.3.3 Long Butterfly Spread Table 8. Long Butterfly Spread. The Value Matrix S<E1 E1<S<E2 E2<S<E3 S>E3 Call (E1) -C1 -C1 + S - E1 -C1 + S - E1 -C1 + S - E1 Call (E3) -C3 -C3 -C3 -C3 + S - E3 - Call (E2) +2C2 +2C2 +2C2 - 2(S - E2) +2C2 - 2(S - E2) Total payoff 2C2 -C1-C3 S - E1 -S + 2E2 - E1 2E2 - E1 - E3 +2C2 -C1-C3 +2C2 -C1-C3 +2C2 -C1-C3 Profit Break-even Point S=E1+(C1+C3-2C2) /Loss Break-even Point S=E3-(C1+C3-2C2) E2-E1-C1-C3+2C2 E1 E2 E3 Spot Price (S) 2C2-C1-C3 Figure 8. Long Butterfly Spread 8 Derivatives Market 231231-0345 1.3.4 Long Condor Table 9. Long Condor. The Value Matrix S<E1 E1<S<E2 E2<S<E3 E3<S<E4 S>E4 Call (E1) -C1 -C1 + S - E1 -C1 + S - E1 -C1 + S - E1 -C1 + S - E1 - Call (E2) +C2 +C2 +C2 - S + E2 +C2 - S + E2 +C2 - S + E2 - Call (E3) +C3 +C3 +C3 +C3 - S + E3 +C3 - S + E3 Call (E4) -C4 -C4 -C4 -C4 -C4 + S - E4 Total payoff -C S - E1 - C E2 - E1 - C E3 + E2 - E1 - S E3 + E2 - E1 - - C E4 - C Profit Break-even Point S=E1+C1+C4-C2-C3 /Loss E2-E1 Break-even Point S=E4-(C1+C4-C2-C3) E2-E1-C1-C4+C2+C3 E1 E2 E3 E4 Spot Price (S) -C1-C4+C2+C3 Figure 9. Long Condor 9 Derivatives Market 231231-0345 1.4 Market scenario bulish. Volatility undecided 1.4.1 Long Call + Short Put Long call and short put replicates long share. 1.4.2 Bull Spread Table 10. Bull Call Spread. The Value Matrix S<E1 E1<S<E2 S>E2 Call (E1) -C1 -C1 + S - E1 -C1 + S - E1 - Call (E2) +C2 +C2 +C2 - S + E2 Total payoff C2 -C1 + S - E1+C2 -C1 E2 - E1 +C2 -C1 Profit /Loss Break-even Point S=E1+C1-C2 E2-E1 C2-C1 E1 E2 Spot Price (S) Figure 10. Bull Call Spread 10 Derivatives Market 231231-0345 1.4.3 Rotated Vertical Bull Spread Table 11. Rotated Vertical Bull Spread. The Value Matrix S<E S>E Call -C0 -C0 + S - E - Put +P0 - (E - S) + P0 Total payoff S - E - C0 + P0 + S - E - C0 + P0 Profit /Loss Break-even Point S=E-P0+C0 CF=P0-C0 E Spot Price (S) Premium Figure 11. Rotated Vertical Bull Spread 11 Derivatives Market 231231-0345 1.5 Market scenario bulish. Volatility rising 1.5.1 Long Call Long call is the simplest strategy for an investor expecting rise in prices and rise in volatility. 1.5.2 Protective Put Table 12. Protective Put. The Value Matrix S<E S>E Long share S S Put -P0 + E - S - P0 Total payoff E -P0 S - P0 Long share Profit /Loss E CF=P0 Break-even Point Premium S=E-P0 E Spot Price (S) Figure 12. Protective Put 12 Derivatives Market 231231-0345 1.5.3 Call Ratio Back Spread Table 13. Call Ratio Back Spread. The Value Matrix S<E1 E1<S<E2 S>E2 - Call (E1) +C1 +C1 - S + E1 +C1 - S + E1 Two calls (E2) -2C2 -2C2 -2C2 + 2 (S - E2) Total payoff +C1 - 2C2 - S + E1 + C1 - 2C2 S + E1 - 2E2 +C1 - 2C2 Profit /Loss Break-even Point S=2E2-E1+2C2-C1 C1-2C2 E1 E2 Spot Price (S) E1-E2+C1-2C2 E1-E2 Figure 13. Call Ratio Back Spread 13 Derivatives Market 231231-0345 1.6 Market scenario bulish. Volatility falling 1.6.1 Short Put Short put is the simplest strategy for an investor expecting fall in prices and fall in volatility. 1.6.2 Covered Call Table 14. Covered Call. The Value Matrix S<E S>E Long share S S - Call +C0 +C0 - (S - E) Total payoff S + C0 E + C0 Long share Profit /Loss E Break-even Point S=E+C0 CF=C0 Premium E Spot Price (S) Figure 14. Covered Call 14 Derivatives Market 231231-0345 1.6.3 Ratio Call Spread Table 15. Ratio Call Spread. The Value Matrix S<E1 E1<S<E2 S>E2 Call (E1) -C1 -C1 + S - E1 -C1 + S - E1 Two short Puts (E2) +2C2 +2C2 +2C2 - 2( S - E2) Total payoff -C1 + 2C2 + S - E1 - C1 + 2C2 -S - E1 + 2E2 -C1 + 2C2 Profit /Loss E2-E1+2C2-C1 Break-even Point S=2E2-E1+2C2-C1 E2-E1 2C2-C1 E1 E2 Spot Price (S) (2C2<C1) Figure 15. Ratio Call Spread 15 Derivatives Market 231231-0345 1.7 Market scenario bearish. Volatility undecided 1.7.1 Short Call + Long Put Short call and long put replicates short share or short futures. 1.7.2 Bear Spread Table 16. Bear Put Spread. The Value Matrix S<E1 E1<S<E2 S>E2 Put (E2) -P2 + E2 - S -P2 + E2 - S - P2 - Put (E1) +P1 - (E1 - S) + P1 + P1 Total payoff +P1 - P2 + E2 - E1 + P1 - P2 + E2 - S + P1- P2 Profit /Loss Break-even Point S=E2+P1-P2 E2-E1 E2-E1+P1-P2 P1-P2 E1 E2 Spot Price (S) Figure 16. Bear Put Spread 16 Derivatives Market 231231-0345 1.7.3 Rotated Vertical Bear Spread Table 17. Rotated Vertical Bear Spread.
Load more

Recommended publications
  • Here We Go Again
    2015, 2016 MDDC News Organization of the Year! Celebrating 161 years of service! Vol. 163, No. 3 • 50¢ SINCE 1855 July 13 - July 19, 2017 TODAY’S GAS Here we go again . PRICE Rockville political differences rise to the surface in routine commission appointment $2.28 per gallon Last Week pointee to the City’s Historic District the three members of “Team him from serving on the HDC. $2.26 per gallon By Neal Earley @neal_earley Commission turned into a heated de- Rockville,” a Rockville political- The HDC is responsible for re- bate highlighting the City’s main po- block made up of Council members viewing applications for modification A month ago ROCKVILLE – In most jurisdic- litical division. Julie Palakovich Carr, Mark Pierzcha- to the exteriors of historic buildings, $2.36 per gallon tions, board and commission appoint- Mayor Bridget Donnell Newton la and Virginia Onley who ran on the as well as recommending boundaries A year ago ments are usually toward the bottom called the City Council’s rejection of same platform with mayoral candi- for the City’s historic districts. If ap- $2.28 per gallon of the list in terms of public interest her pick for Historic District Commis- date Sima Osdoby and city council proved Giammo, would have re- and controversy -- but not in sion – former three-term Rockville candidate Clark Reed. placed Matthew Goguen, whose term AVERAGE PRICE PER GALLON OF Rockville. UNLEADED REGULAR GAS IN Mayor Larry Giammo – political. While Onley and Palakovich expired in May. MARYLAND/D.C. METRO AREA For many municipalities, may- “I find it absolutely disappoint- Carr said they opposed Giammo’s ap- Giammo previously endorsed ACCORDING TO AAA oral appointments are a formality of- ing that politics has entered into the pointment based on his lack of qualifi- Newton in her campaign against ten given rubberstamped approval by boards and commission nomination cations, Giammo said it was his polit- INSIDE the city council, but in Rockville what process once again,” Newton said.
    [Show full text]
  • Up to EUR 3,500,000.00 7% Fixed Rate Bonds Due 6 April 2026 ISIN
    Up to EUR 3,500,000.00 7% Fixed Rate Bonds due 6 April 2026 ISIN IT0005440976 Terms and Conditions Executed by EPizza S.p.A. 4126-6190-7500.7 This Terms and Conditions are dated 6 April 2021. EPizza S.p.A., a company limited by shares incorporated in Italy as a società per azioni, whose registered office is at Piazza Castello n. 19, 20123 Milan, Italy, enrolled with the companies’ register of Milan-Monza-Brianza- Lodi under No. and fiscal code No. 08950850969, VAT No. 08950850969 (the “Issuer”). *** The issue of up to EUR 3,500,000.00 (three million and five hundred thousand /00) 7% (seven per cent.) fixed rate bonds due 6 April 2026 (the “Bonds”) was authorised by the Board of Directors of the Issuer, by exercising the powers conferred to it by the Articles (as defined below), through a resolution passed on 26 March 2021. The Bonds shall be issued and held subject to and with the benefit of the provisions of this Terms and Conditions. All such provisions shall be binding on the Issuer, the Bondholders (and their successors in title) and all Persons claiming through or under them and shall endure for the benefit of the Bondholders (and their successors in title). The Bondholders (and their successors in title) are deemed to have notice of all the provisions of this Terms and Conditions and the Articles. Copies of each of the Articles and this Terms and Conditions are available for inspection during normal business hours at the registered office for the time being of the Issuer being, as at the date of this Terms and Conditions, at Piazza Castello n.
    [Show full text]
  • Introduction to Options
    FIN-40008 FINANCIAL INSTRUMENTS SPRING 2008 Options These notes describe the payoffs to European and American put and call options|the so-called plain vanilla options. We consider the payoffs to these options for holders and writers and describe both the time vale and intrinsic value of an option. We explain why options are traded and examine some of the properties of put and call option prices. We shall show that longer dated options typically have higher prices and that call prices are higher when the strike price is lower and that put prices are higher when the strike price is higher. Keywords: Put, call, strike price, maturity date, in-the-money, time value, intrinsic value, parity value, American option, European option, early exer- cise, bull spread, bear spread, butterfly spread. 1 Options Options are derivative assets. That is their payoffs are derived from the pay- off on some other underlying asset. The underlying asset may be an equity, an index, a bond or indeed any other type of asset. Options themselves are classified by their type, class and their series. The most important distinc- tion of types is between put options and call options. A put option gives the owner the right to sell the underlying asset at specified dates at a specified price. A call option gives the owner the right to buy at specified dates at a specified price. Options are different from forward/futures contracts as a put (call) option gives the owner right to sell (buy) the underlying asset but not an obligation. The right to buy or sell need not be exercised.
    [Show full text]
  • (NSE), India, Using Box Spread Arbitrage Strategy
    Gadjah Mada International Journal of Business - September-December, Vol. 15, No. 3, 2013 Gadjah Mada International Journal of Business Vol. 15, No. 3 (September - December 2013): 269 - 285 Efficiency of S&P CNX Nifty Index Option of the National Stock Exchange (NSE), India, using Box Spread Arbitrage Strategy G. P. Girish,a and Nikhil Rastogib a IBS Hyderabad, ICFAI Foundation For Higher Education (IFHE) University, Andhra Pradesh, India b Institute of Management Technology (IMT) Hyderabad, India Abstract: Box spread is a trading strategy in which one simultaneously buys and sells options having the same underlying asset and time to expiration, but different exercise prices. This study examined the effi- ciency of European style S&P CNX Nifty Index options of National Stock Exchange, (NSE) India by making use of high-frequency data on put and call options written on Nifty (Time-stamped transactions data) for the time period between 1st January 2002 and 31st December 2005 using box-spread arbitrage strategy. The advantages of box-spreads include reduced joint hypothesis problem since there is no consideration of pricing model or market equilibrium, no consideration of inter-market non-synchronicity since trading box spreads involve only one market, computational simplicity with less chances of mis- specification error, estimation error and the fact that buying and selling box spreads more or less repli- cates risk-free lending and borrowing. One thousand three hundreds and fifty eight exercisable box- spreads were found for the time period considered of which 78 Box spreads were found to be profit- able after incorporating transaction costs (32 profitable box spreads were identified for the year 2002, 19 in 2003, 14 in 2004 and 13 in 2005) The results of our study suggest that internal option market efficiency has improved over the years for S&P CNX Nifty Index options of NSE India.
    [Show full text]
  • How Options Implied Probabilities Are Calculated
    No content left No content right of this line of this line How Options Implied Probabilities Are Calculated The implied probability distribution is an approximate risk-neutral distribution derived from traded option prices using an interpolated volatility surface. In a risk-neutral world (i.e., where we are not more adverse to losing money than eager to gain it), the fair price for exposure to a given event is the payoff if that event occurs, times the probability of it occurring. Worked in reverse, the probability of an outcome is the cost of exposure Place content to the outcome divided by its payoff. Place content below this line below this line In the options market, we can buy exposure to a specific range of stock price outcomes with a strategy know as a butterfly spread (long 1 low strike call, short 2 higher strikes calls, and long 1 call at an even higher strike). The probability of the stock ending in that range is then the cost of the butterfly, divided by the payout if the stock is in the range. Building a Butterfly: Max payoff = …add 2 …then Buy $5 at $55 Buy 1 50 short 55 call 1 60 call calls Min payoff = $0 outside of $50 - $60 50 55 60 To find a smooth distribution, we price a series of theoretical call options expiring on a single date at various strikes using an implied volatility surface interpolated from traded option prices, and with these calls price a series of very tight overlapping butterfly spreads. Dividing the costs of these trades by their payoffs, and adjusting for the time value of money, yields the future probability distribution of the stock as priced by the options market.
    [Show full text]
  • Chapter 2 Roche Holding: the Company, Its
    Risk Takers Uses and Abuses of Financial Derivatives John E. Marthinsen Babson College PEARSON Addison Wesley Boston San Francisco New York London Toronto Sydney Tokyo Singapore Madrid Mexico City Munich Paris Cape Town Hong Kong Montreal Preface xiii Parti 1 Chapter 1 Employee Stock Options: What Every MBA Should Know 3 Introduction 3 Employee Stock Options: A Major Pillar of Executive Compensation 6 Why Do Companies Use Employee Stock Options 6 Aligning Incentives 7 Hiring and Retention 7 Postponing the Timing of Expenses 8 Adjusting Compensation to Employee Risk Tolerance Levels 8 Tax Advantages for Employees 9 Tax Advantages for Companies 9 Cash Flow Advantages for Companies 10 Option Valuation Differences and Human Resource Management 12 Problems with Employee Stock Options 26 Employee Motivation 26 The Share Price of "Good" Companies 27 Motivation of Undesired Behavior 28 vi Contents Performance Improvement 28 Absolute Versus Relative Performance 29 Some Innovative Solutions to Employee Stock Option Problems 29 Premium-Priced Stock Options 30 Index Options 30 Restricted Shares 34 Omnibus Plans 34 Conclusion 35 Review Questions 36 Bibliography 38 Chapter 2 Roche Holding: The Company, Its Financial Strategy, and Bull Spread Warrants 41 Introduction 41 Roche Holding AG: Transition from a Lender to a Borrower 43 Loss of the Valium Patent in the United States 43 Rapid Increase in R&D Costs, Market Growth, and Industry Consolidation 43 Roche's Unique Capital Structure 44 Roche Brings in a New Leader and Replaces Its Management Committee
    [Show full text]
  • Module 6 Option Strategies.Pdf
    zerodha.com/varsity TABLE OF CONTENTS 1 Orientation 1 1.1 Setting the context 1 1.2 What should you know? 3 2 Bull Call Spread 6 2.1 Background 6 2.2 Strategy notes 8 2.3 Strike selection 14 3 Bull Put spread 22 3.1 Why Bull Put Spread? 22 3.2 Strategy notes 23 3.3 Other strike combinations 28 4 Call ratio back spread 32 4.1 Background 32 4.2 Strategy notes 33 4.3 Strategy generalization 38 4.4 Welcome back the Greeks 39 5 Bear call ladder 46 5.1 Background 46 5.2 Strategy notes 46 5.3 Strategy generalization 52 5.4 Effect of Greeks 54 6 Synthetic long & arbitrage 57 6.1 Background 57 zerodha.com/varsity 6.2 Strategy notes 58 6.3 The Fish market Arbitrage 62 6.4 The options arbitrage 65 7 Bear put spread 70 7.1 Spreads versus naked positions 70 7.2 Strategy notes 71 7.3 Strategy critical levels 75 7.4 Quick notes on Delta 76 7.5 Strike selection and effect of volatility 78 8 Bear call spread 83 8.1 Choosing Calls over Puts 83 8.2 Strategy notes 84 8.3 Strategy generalization 88 8.4 Strike selection and impact of volatility 88 9 Put ratio back spread 94 9.1 Background 94 9.2 Strategy notes 95 9.3 Strategy generalization 99 9.4 Delta, strike selection, and effect of volatility 100 10 The long straddle 104 10.1 The directional dilemma 104 10.2 Long straddle 105 10.3 Volatility matters 109 10.4 What can go wrong with the straddle? 111 zerodha.com/varsity 11 The short straddle 113 11.1 Context 113 11.2 The short straddle 114 11.3 Case study 116 11.4 The Greeks 119 12 The long & short straddle 121 12.1 Background 121 12.2 Strategy notes 122 12..3 Delta and Vega 128 12.4 Short strangle 129 13 Max pain & PCR ratio 130 13.1 My experience with option theory 130 13.2 Max pain theory 130 13.3 Max pain calculation 132 13.4 A few modifications 137 13.5 The put call ratio 138 13.6 Final thoughts 140 zerodha.com/varsity CHAPTER 1 Orientation 1.1 – Setting the context Before we start this module on Option Strategy, I would like to share with you a Behavioral Finance article I read couple of years ago.
    [Show full text]
  • Tax Treatment of Derivatives
    United States Viva Hammer* Tax Treatment of Derivatives 1. Introduction instruments, as well as principles of general applicability. Often, the nature of the derivative instrument will dictate The US federal income taxation of derivative instruments whether it is taxed as a capital asset or an ordinary asset is determined under numerous tax rules set forth in the US (see discussion of section 1256 contracts, below). In other tax code, the regulations thereunder (and supplemented instances, the nature of the taxpayer will dictate whether it by various forms of published and unpublished guidance is taxed as a capital asset or an ordinary asset (see discus- from the US tax authorities and by the case law).1 These tax sion of dealers versus traders, below). rules dictate the US federal income taxation of derivative instruments without regard to applicable accounting rules. Generally, the starting point will be to determine whether the instrument is a “capital asset” or an “ordinary asset” The tax rules applicable to derivative instruments have in the hands of the taxpayer. Section 1221 defines “capital developed over time in piecemeal fashion. There are no assets” by exclusion – unless an asset falls within one of general principles governing the taxation of derivatives eight enumerated exceptions, it is viewed as a capital asset. in the United States. Every transaction must be examined Exceptions to capital asset treatment relevant to taxpayers in light of these piecemeal rules. Key considerations for transacting in derivative instruments include the excep- issuers and holders of derivative instruments under US tions for (1) hedging transactions3 and (2) “commodities tax principles will include the character of income, gain, derivative financial instruments” held by a “commodities loss and deduction related to the instrument (ordinary derivatives dealer”.4 vs.
    [Show full text]
  • Bond Futures Calendar Spread Trading
    Black Algo Technologies Bond Futures Calendar Spread Trading Part 2 – Understanding the Fundamentals Strategy Overview Asset to be traded: Three-month Canadian Bankers' Acceptance Futures (BAX) Price chart of BAXH20 Strategy idea: Create a duration neutral (i.e. market neutral) synthetic asset and trade the mean reversion The general idea is straightforward to most professional futures traders. This is not some market secret. The success of this strategy lies in the execution. Understanding Our Asset and Synthetic Asset These are the prices and volume data of BAX as seen in the Interactive Brokers platform. blackalgotechnologies.com Black Algo Technologies Notice that the volume decreases as we move to the far month contracts What is BAX BAX is a future whose underlying asset is a group of short-term (30, 60, 90 days, 6 months or 1 year) loans that major Canadian banks make to each other. BAX futures reflect the Canadian Dollar Offered Rate (CDOR) (the overnight interest rate that Canadian banks charge each other) for a three-month loan period. Settlement: It is cash-settled. This means that no physical products are transferred at the futures’ expiry. Minimum price fluctuation: 0.005, which equates to C$12.50 per contract. This means that for every 0.005 move in price, you make or lose $12.50 Canadian dollar. Link to full specification details: • https://m-x.ca/produits_taux_int_bax_en.php (Note that the minimum price fluctuation is 0.01 for contracts further out from the first 10 expiries. Not too important as we won’t trade contracts that are that far out.) • https://www.m-x.ca/f_publications_en/bax_en.pdf Other STIR Futures BAX are just one type of short-term interest rate (STIR) future.
    [Show full text]
  • Options Slide Deck Updated Version
    www.levelupbootcamps.com 4/4/21 Derivatives Option Strategies 4/4/21 LevelUp, LLC©2021 All rights reserved 1 1 Derivatives & Currency Management Option Strategies 4/4/21 LevelUp, LLC©2021 All rights reserved 2 2 Level Up, LLC©2021 All rights reserved 1 www.levelupbootcamps.com 4/4/21 Risk Management with Options Synthetic Positions • Synthetic Long & Short Forward Option Strategies • Synthetic Puts & Calls Multiple Option Strategies Single Option + Underlying Single Option Directionless Volatility Long U/L Risk Reduction Writing Puts • Long Straddle = LC + LP Covered Call = U/L + SC • Lower purchase cost • Short Straddle = SC + SP • Income enhancement • Fiduciary put = SP + Money Spreads • Reduce at favorable price cash to cover (ftn 13) “Small Moves Up or Down” • Target price realization The Greeks • Bull & Bear Call Spreads • Manza Case 1. Delta + & - • Bear & Bull Put Spreads Protective Put = U/L + LP 2. Gamma + • Insurance Calendar Spreads 3. Theta (time) - Collar = U/L + LP + SC Short “Its all about Theta” 4. Vega (Implied Vol) + • Risk Reversal • Long Calendar Spread Portfolio Mgt • Short Calendar Spread Short U/L Risk Reduction 1. Strategies using • Short U/L + Long Call volatility & market view • Short U/L + Short Put 2. Adjusting risk exposure 4/4/21 LevelUp, LLC©2021 All rights reserved 3 3 Single Option Strategies Refresher . just in case + + X S Long Call – LC S Short Call – SC - - X “writing” Want U/L up – bullish Want U/L down – bearish Right to buy at strike price X Obligated to sell at strike price X Max gain = ∞ when S
    [Show full text]
  • 11 Option Payoffs and Option Strategies
    11 Option Payoffs and Option Strategies Answers to Questions and Problems 1. Consider a call option with an exercise price of $80 and a cost of $5. Graph the profits and losses at expira- tion for various stock prices. 73 74 CHAPTER 11 OPTION PAYOFFS AND OPTION STRATEGIES 2. Consider a put option with an exercise price of $80 and a cost of $4. Graph the profits and losses at expiration for various stock prices. ANSWERS TO QUESTIONS AND PROBLEMS 75 3. For the call and put in questions 1 and 2, graph the profits and losses at expiration for a straddle comprising these two options. If the stock price is $80 at expiration, what will be the profit or loss? At what stock price (or prices) will the straddle have a zero profit? With a stock price at $80 at expiration, neither the call nor the put can be exercised. Both expire worthless, giving a total loss of $9. The straddle breaks even (has a zero profit) if the stock price is either $71 or $89. 4. A call option has an exercise price of $70 and is at expiration. The option costs $4, and the underlying stock trades for $75. Assuming a perfect market, how would you respond if the call is an American option? State exactly how you might transact. How does your answer differ if the option is European? With these prices, an arbitrage opportunity exists because the call price does not equal the maximum of zero or the stock price minus the exercise price. To exploit this mispricing, a trader should buy the call and exercise it for a total out-of-pocket cost of $74.
    [Show full text]
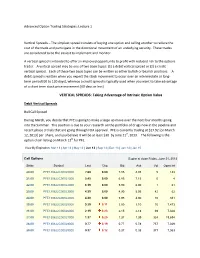
  • VERTICAL SPREADS: Taking Advantage of Intrinsic Option Value
    Advanced Option Trading Strategies: Lecture 1 Vertical Spreads – The simplest spread consists of buying one option and selling another to reduce the cost of the trade and participate in the directional movement of an underlying security. These trades are considered to be the easiest to implement and monitor. A vertical spread is intended to offer an improved opportunity to profit with reduced risk to the options trader. A vertical spread may be one of two basic types: (1) a debit vertical spread or (2) a credit vertical spread. Each of these two basic types can be written as either bullish or bearish positions. A debit spread is written when you expect the stock movement to occur over an intermediate or long- term period [60 to 120 days], whereas a credit spread is typically used when you want to take advantage of a short term stock price movement [60 days or less]. VERTICAL SPREADS: Taking Advantage of Intrinsic Option Value Debit Vertical Spreads Bull Call Spread During March, you decide that PFE is going to make a large up move over the next four months going into the Summer. This position is due to your research on the portfolio of drugs now in the pipeline and recent phase 3 trials that are going through FDA approval. PFE is currently trading at $27.92 [on March 12, 2013] per share, and you believe it will be at least $30 by June 21st, 2013. The following is the option chain listing on March 12th for PFE. View By Expiration: Mar 13 | Apr 13 | May 13 | Jun 13 | Sep 13 | Dec 13 | Jan 14 | Jan 15 Call Options Expire at close Friday,
    [Show full text]