DOCSLIB.ORG

Mental Maths Strategies for Multiplication and Division

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Mental Maths Strategies for Multiplication and Division Practical Approaches to Developing Mental Maths Strategies for Multiplication and Division × ÷ This manual has been designed by members of the Professional Development Service for Teachers. Its sole purpose is to enhance teaching and learning in Irish primary schools and it will be mediated to practising teachers in the professional development setting. Thereafter it will be available as a free downloadable resource on www.pdst.ie for use in the classroom. This resource is strictly the intellectual property of PDST and it is not intended that it be made commercially available through publishers. All ideas, suggestions and activities remain the intellectual property of PDST (all ideas and activities that were sourced elsewhere and are not those of the authors are acknowledged throughout the manual). It is not permitted to use this manual for any purpose other than as a resource to enhance teaching and learning. Any queries related to its usage should be sent in writing to: Professional Development Service for Teachers, 14, Joyce Way, Park West Business Park, Nangor Road, Dublin 12. Contents Introduction ............................................................................................................................................ 4 Background Knowledge for Teachers ..................................................................................................... 5 Stages of Progression .......................................................................................................................... 5 Multiplication Symbol ........................................................................................................................ 5 Known Facts ....................................................................................................................................... 6 Teaching Multiplication and Division .................................................................................................. 6 Dealing with Remainders .................................................................................................................... 6 Division using Arrays ........................................................................................................................... 7 Linear, Area and Set Model for Multiplication and Division ............................................................... 8 Possible Pupil Misconceptions ................................................................................................................ 9 Uses of Mental Calculation ............................................................................................................... 11 Fundamental Facts for Multiplication and Division .............................................................................. 12 The Commutative Property .............................................................................................................. 12 The Associative Property .................................................................................................................. 12 The Distributive Property .................................................................................................................. 12 Inverse Relationship .......................................................................................................................... 12 Teaching and Learning .......................................................................................................................... 13 Suggested Multiplication & Division Strategies ................................................................................ 13 Instructional Framework ................................................................................................................... 14 Classroom Culture ............................................................................................................................. 16 Problems and Solutions in Supporting and Developing Mathematical Thinking ............................. 17 Possible Resources ............................................................................................................................ 18 Key Teaching Principles for Mental Maths ....................................................................................... 18 Assessment ....................................................................................................................................... 19 Teacher Manuals for Supporting and Developing Mathematical Thinking ...................................... 20 Practical Strategies to Develop Multiplication and Division Properties ............................................... 21 Commutative Property ..................................................................................................................... 21 Distributive property of multiplication ............................................................................................. 22 1 Practical Activities for developing Multiplication & Division Strategies ............................................... 24 Skip counting ..................................................................................................................................... 24 Skip Counting for Division ................................................................................................................. 25 Multiplication Strategy: Repeated Addition ..................................................................................... 25 Repeated Subtraction for Division .................................................................................................... 27 Division as inverse multiplication with Cuisenaire Rods ................................................................... 30 Division as inverse multiplication- Area ............................................................................................ 31 Multiplication & Division Fact Families ............................................................................................. 32 Multiplication Strategy: Doubles ...................................................................................................... 33 Double and one more set ................................................................................................................. 33 Double and Double Again ................................................................................................................. 34 Multiplication Strategy: Known Facts ............................................................................................... 35 Multiples of 10 (links to facts for doubles, known facts and counting stick activities) .................... 35 Rounding and Compensating Strategy ............................................................................................. 35 Making Friendly Numbers Strategy .................................................................................................. 37 Partitioning Strategies ...................................................................................................................... 38 Partial Products ................................................................................................................................. 39 Division Strategy: Partial Quotients .................................................................................................. 42 Doubling/Halving .............................................................................................................................. 43 Pose the following problem to the children: .................................................................................... 47 Proportional Reasoning/Adjustment for division ............................................................................. 48 Breaking Factors into Smaller Factors and Factorisation.................................................................. 49 Think Multiplication for Division ....................................................................................................... 51 Towards Fluency and Consolidation in Applying Strategies ................................................................. 53 Counting Activities using Multiplication and Division........................................................................... 58 Possible Sequence for Developing Multiplication Facts ....................................................................... 61 Further Examples for Exploring and Embedding Strategies ................................................................. 64 References ............................................................................................................................................ 67 2 3 Introduction This booklet is intended to support teachers in developing multiplication and division mental maths strategies in their classrooms. It has been designed to accompany the PDST Mental Maths workshops. The booklet explores the key properties of number and number relationships relating to multiplication and division and outlines practical approaches to developing an understanding of these. It also explores background knowledge for teachers and fundamental facts in relation to mental maths. A range of concrete, practical activities that will support pupils in their development of multiplication and division mental maths strategies are also outlined. Also included is a suggested alternative strategic sequence through which pupils may acquire their multiplication facts. Finally,
Load more

Recommended publications
  • Division by Zero Calculus and Singular Integrals
    Proceedings of International Conference on Mechanical, Electrical and Medical Intelligent System 2017 Division by Zero Calculus and Singular Integrals Tsutomu Matsuura1, a and Saburou Saitoh2,b 1Faculty of Science and Technology, Gunma University, 1-5-1 Tenjin-cho, Kiryu 376-8515, Japan 2Institute of Reproducing Kernels, Kawauchi-cho, 5-1648-16, Kiryu 376-0041, Japan [email protected], [email protected] Keywords: division by zero, point at infinity, singularity, Laurent expansion, Hadamard finite part Abstract. In this paper, we will introduce the formulas log 0= log ∞= 0 (not as limiting values) in the meaning of the one point compactification of Aleksandrov and their fundamental applications, and we will also examine the relationship between Laurent expansion and the division by zero. Based on those examinations we give the interpretation for the Hadamard finite part of singular integrals by means of the division by zero calculus. In particular, we will know that the division by zero is our elementary and fundamental mathematics. 1. Introduction By a natural extension of the fractions b (1) a for any complex numbers a and b , we found the simple and beautiful result, for any complex number b b = 0, (2) 0 incidentally in [1] by the Tikhonov regularization for the Hadamard product inversions for matrices and we discussed their properties and gave several physical interpretations on the general fractions in [2] for the case of real numbers. The result is very special case for general fractional functions in [3]. The division by zero has a long and mysterious story over the world (see, for example, H.
    [Show full text]
  • The Role of the Interval Domain in Modern Exact Real Airthmetic
    The Role of the Interval Domain in Modern Exact Real Airthmetic Andrej Bauer Iztok Kavkler Faculty of Mathematics and Physics University of Ljubljana, Slovenia Domains VIII & Computability over Continuous Data Types Novosibirsk, September 2007 Teaching theoreticians a lesson Recently I have been told by an anonymous referee that “Theoreticians do not like to be taught lessons.” and by a friend that “You should stop competing with programmers.” In defiance of this advice, I shall talk about the lessons I learned, as a theoretician, in programming exact real arithmetic. The spectrum of real number computation slow fast Formally verified, Cauchy sequences iRRAM extracted from streams of signed digits RealLib proofs floating point Moebius transformtions continued fractions Mathematica "theoretical" "practical" I Common features: I Reals are represented by successive approximations. I Approximations may be computed to any desired accuracy. I State of the art, as far as speed is concerned: I iRRAM by Norbert Muller,¨ I RealLib by Branimir Lambov. What makes iRRAM and ReaLib fast? I Reals are represented by sequences of dyadic intervals (endpoints are rationals of the form m/2k). I The approximating sequences need not be nested chains of intervals. I No guarantee on speed of converge, but arbitrarily fast convergence is possible. I Previous approximations are not stored and not reused when the next approximation is computed. I Each next approximation roughly doubles the amount of work done. The theory behind iRRAM and RealLib I Theoretical models used to design iRRAM and RealLib: I Type Two Effectivity I a version of Real RAM machines I Type I representations I The authors explicitly reject domain theory as a suitable computational model.
    [Show full text]
  • Division by Fractions 6.1.1 - 6.1.4
    DIVISION BY FRACTIONS 6.1.1 - 6.1.4 Division by fractions introduces three methods to help students understand how dividing by fractions works. In general, think of division for a problem like 8..,.. 2 as, "In 8, how many groups of 2 are there?" Similarly, ½ + ¼ means, "In ½ , how many fourths are there?" For more information, see the Math Notes boxes in Lessons 7.2 .2 and 7 .2 .4 of the Core Connections, Course 1 text. For additional examples and practice, see the Core Connections, Course 1 Checkpoint 8B materials. The first two examples show how to divide fractions using a diagram. Example 1 Use the rectangular model to divide: ½ + ¼ . Step 1: Using the rectangle, we first divide it into 2 equal pieces. Each piece represents ½. Shade ½ of it. - Step 2: Then divide the original rectangle into four equal pieces. Each section represents ¼ . In the shaded section, ½ , there are 2 fourths. 2 Step 3: Write the equation. Example 2 In ¾ , how many ½ s are there? In ¾ there is one full ½ 2 2 I shaded and half of another Thatis,¾+½=? one (that is half of one half). ]_ ..,_ .l 1 .l So. 4 . 2 = 2 Start with ¾ . 3 4 (one and one-half halves) Parent Guide with Extra Practice © 2011, 2013 CPM Educational Program. All rights reserved. 49 Problems Use the rectangular model to divide. .l ...:... J_ 1 ...:... .l 1. ..,_ l 1 . 1 3 . 6 2. 3. 4. 1 4 . 2 5. 2 3 . 9 Answers l. 8 2. 2 3. 4 one thirds rm I I halves - ~I sixths fourths fourths ~I 11 ~'.¿;¡~:;¿~ ffk] 8 sixths 2 three fourths 4.
    [Show full text]
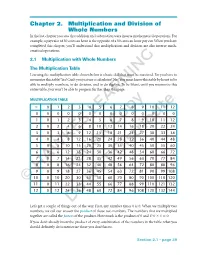
  • Chapter 2. Multiplication and Division of Whole Numbers in the Last Chapter You Saw That Addition and Subtraction Were Inverse Mathematical Operations
    Chapter 2. Multiplication and Division of Whole Numbers In the last chapter you saw that addition and subtraction were inverse mathematical operations. For example, a pay raise of 50 cents an hour is the opposite of a 50 cents an hour pay cut. When you have completed this chapter, you’ll understand that multiplication and division are also inverse math- ematical operations. 2.1 Multiplication with Whole Numbers The Multiplication Table Learning the multiplication table shown below is a basic skill that must be mastered. Do you have to memorize this table? Yes! Can’t you just use a calculator? No! You must know this table by heart to be able to multiply numbers, to do division, and to do algebra. To be blunt, until you memorize this entire table, you won’t be able to progress further than this page. MULTIPLICATION TABLE ϫ 012 345 67 89101112 0 000 000LEARNING 00 000 00 1 012 345 67 89101112 2 024 681012Copy14 16 18 20 22 24 3 036 9121518212427303336 4 0481216 20 24 28 32 36 40 44 48 5051015202530354045505560 6061218243036424854606672Distribute 7071421283542495663707784 8081624324048566472808896 90918273HAWKESReview645546372819099108 10 0 10 20 30 40 50 60 70 80 90 100 110 120 ©11 0 11 22 33 44NOT 55 66 77 88 99 110 121 132 12 0 12 24 36 48 60 72 84 96 108 120 132 144 Do Let’s get a couple of things out of the way. First, any number times 0 is 0. When we multiply two numbers, we call our answer the product of those two numbers.
    [Show full text]
  • Division by Zero in Logic and Computing Jan Bergstra
    Division by Zero in Logic and Computing Jan Bergstra To cite this version: Jan Bergstra. Division by Zero in Logic and Computing. 2021. hal-03184956v2 HAL Id: hal-03184956 https://hal.archives-ouvertes.fr/hal-03184956v2 Preprint submitted on 19 Apr 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. DIVISION BY ZERO IN LOGIC AND COMPUTING JAN A. BERGSTRA Abstract. The phenomenon of division by zero is considered from the per- spectives of logic and informatics respectively. Division rather than multi- plicative inverse is taken as the point of departure. A classification of views on division by zero is proposed: principled, physics based principled, quasi- principled, curiosity driven, pragmatic, and ad hoc. A survey is provided of different perspectives on the value of 1=0 with for each view an assessment view from the perspectives of logic and computing. No attempt is made to survey the long and diverse history of the subject. 1. Introduction In the context of rational numbers the constants 0 and 1 and the operations of addition ( + ) and subtraction ( − ) as well as multiplication ( · ) and division ( = ) play a key role. When starting with a binary primitive for subtraction unary opposite is an abbreviation as follows: −x = 0 − x, and given a two-place division function unary inverse is an abbreviation as follows: x−1 = 1=x.
    [Show full text]
  • IEEE Standard 754 for Binary Floating-Point Arithmetic
    Work in Progress: Lecture Notes on the Status of IEEE 754 October 1, 1997 3:36 am Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic Prof. W. Kahan Elect. Eng. & Computer Science University of California Berkeley CA 94720-1776 Introduction: Twenty years ago anarchy threatened floating-point arithmetic. Over a dozen commercially significant arithmetics boasted diverse wordsizes, precisions, rounding procedures and over/underflow behaviors, and more were in the works. “Portable” software intended to reconcile that numerical diversity had become unbearably costly to develop. Thirteen years ago, when IEEE 754 became official, major microprocessor manufacturers had already adopted it despite the challenge it posed to implementors. With unprecedented altruism, hardware designers had risen to its challenge in the belief that they would ease and encourage a vast burgeoning of numerical software. They did succeed to a considerable extent. Anyway, rounding anomalies that preoccupied all of us in the 1970s afflict only CRAY X-MPs — J90s now. Now atrophy threatens features of IEEE 754 caught in a vicious circle: Those features lack support in programming languages and compilers, so those features are mishandled and/or practically unusable, so those features are little known and less in demand, and so those features lack support in programming languages and compilers. To help break that circle, those features are discussed in these notes under the following headings: Representable Numbers, Normal and Subnormal, Infinite
    [Show full text]
  • Classical Logic and the Division by Zero Ilija Barukčić#1 #Internist Horandstrasse, DE-26441 Jever, Germany
    International Journal of Mathematics Trends and Technology (IJMTT) – Volume 65 Issue 8 – August 2019 Classical logic and the division by zero Ilija Barukčić#1 #Internist Horandstrasse, DE-26441 Jever, Germany Abstract — The division by zero turned out to be a long lasting and not ending puzzle in mathematics and physics. An end of this long discussion appears not to be in sight. In particular zero divided by zero is treated as indeterminate thus that a result cannot be found out. It is the purpose of this publication to solve the problem of the division of zero by zero while relying on the general validity of classical logic. A systematic re-analysis of classical logic and the division of zero by zero has been undertaken. The theorems of this publication are grounded on classical logic and Boolean algebra. There is some evidence that the problem of zero divided by zero can be solved by today’s mathematical tools. According to classical logic, zero divided by zero is equal to one. Keywords — Indeterminate forms, Classical logic, Zero divided by zero, Infinity I. INTRODUCTION Aristotle‘s unparalleled influence on the development of scientific knowledge in western world is documented especially by his contributions to classical logic too. Besides of some serious limitations of Aristotle‘s logic, Aristotle‘s logic became dominant and is still an adequate basis of our understanding of science to some extent, since centuries. In point of fact, some authors are of the opinion that Aristotle himself has discovered everything there was to know about classical logic. After all, classical logic as such is at least closely related to the study of objective reality and deals with absolutely certain inferences and truths.
    [Show full text]
  • Complete Interval Arithmetic and Its Implementation on the Computer
    Complete Interval Arithmetic and its Implementation on the Computer Ulrich W. Kulisch Institut f¨ur Angewandte und Numerische Mathematik Universit¨at Karlsruhe Abstract: Let IIR be the set of closed and bounded intervals of real numbers. Arithmetic in IIR can be defined via the power set IPIR (the set of all subsets) of real numbers. If divisors containing zero are excluded, arithmetic in IIR is an algebraically closed subset of the arithmetic in IPIR, i.e., an operation in IIR performed in IPIR gives a result that is in IIR. Arithmetic in IPIR also allows division by an interval that contains zero. Such division results in closed intervals of real numbers which, however, are no longer bounded. The union of the set IIR with these new intervals is denoted by (IIR). The paper shows that arithmetic operations can be extended to all elements of the set (IIR). On the computer, arithmetic in (IIR) is approximated by arithmetic in the subset (IF ) of closed intervals over the floating-point numbers F ⊂ IR. The usual exceptions of floating-point arithmetic like underflow, overflow, division by zero, or invalid operation do not occur in (IF ). Keywords: computer arithmetic, floating-point arithmetic, interval arithmetic, arith- metic standards. 1 Introduction or a Vision of Future Computing Computers are getting ever faster. The time can already be foreseen when the P C will be a teraflops computer. With this tremendous computing power scientific computing will experience a significant shift from floating-point arithmetic toward increased use of interval arithmetic. With very little extra hardware, interval arith- metic can be made as fast as simple floating-point arithmetic [3].
    [Show full text]
  • Fast Integer Division – a Differentiated Offering from C2000 Product Family
    Application Report SPRACN6–July 2019 Fast Integer Division – A Differentiated Offering From C2000™ Product Family Prasanth Viswanathan Pillai, Himanshu Chaudhary, Aravindhan Karuppiah, Alex Tessarolo ABSTRACT This application report provides an overview of the different division and modulo (remainder) functions and its associated properties. Later, the document describes how the different division functions can be implemented using the C28x ISA and intrinsics supported by the compiler. Contents 1 Introduction ................................................................................................................... 2 2 Different Division Functions ................................................................................................ 2 3 Intrinsic Support Through TI C2000 Compiler ........................................................................... 4 4 Cycle Count................................................................................................................... 6 5 Summary...................................................................................................................... 6 6 References ................................................................................................................... 6 List of Figures 1 Truncated Division Function................................................................................................ 2 2 Floored Division Function................................................................................................... 3 3 Euclidean
    [Show full text]
  • Multiplication and Divisions
    Third Grade Math nd 2 Grading Period Power Objectives: Academic Vocabulary: multiplication array Represent and solve problems involving multiplication and divisor commutative division. (P.O. #1) property Understand properties of multiplication and the distributive property relationship between multiplication and divisions. estimation division factor column (P.O. #2) Multiply and divide with 100. (P.O. #3) repeated addition multiple Solve problems involving the four operations, and identify associative property quotient and explain the patterns in arithmetic. (P.O. #4) rounding row product equation Multiplication and Division Enduring Understandings: Essential Questions: Mathematical operations are used in solving problems In what ways can operations affect numbers? in which a new value is produced from one or more How can different strategies be helpful when solving a values. problem? Algebraic thinking involves choosing, combining, and How does knowing and using algorithms help us to be applying effective strategies for answering questions. Numbers enable us to use the four operations to efficient problem solvers? combine and separate quantities. How are multiplication and addition alike? See below for additional enduring understandings. How are subtraction and division related? See below for additional essential questions. Enduring Understandings: Multiplication is repeated addition, related to division, and can be used to solve story problems. For a given set of numbers, there are relationships that
    [Show full text]
  • AUTHOR Multiplication and Division. Mathematics-Methods
    DOCUMENT RESUME ED 221 338 SE 035 008, AUTHOR ,LeBlanc, John F.; And Others TITLE Multiplication and Division. Mathematics-Methods 12rogram Unipt. INSTITUTION Indiana ,Univ., Bloomington. Mathematics Education !Development Center. , SPONS AGENCY ,National Science Foundation, Washington, D.C. REPORT NO :ISBN-0-201-14610-x PUB DATE 76 . GRANT. NSF-GY-9293 i 153p.; For related documents, see SE 035 006-018. NOTE . ,. EDRS PRICE 'MF01 Plus Postage. PC Not Available from EDRS. DESCRIPTORS iAlgorithms; College Mathematics; *Division; Elementary Education; *Elementary School Mathematics; 'Elementary School Teachers; Higher Education; 'Instructional1 Materials; Learning Activities; :*Mathematics Instruction; *Multiplication; *Preservice Teacher Education; Problem Solving; :Supplementary Reading Materials; Textbooks; ;Undergraduate Study; Workbooks IDENTIFIERS i*Mathematics Methods Program ABSTRACT This unit is 1 of 12 developed for the university classroom portign_of the Mathematics-Methods Program(MMP), created by the Indiana pniversity Mathematics EducationDevelopment Center (MEDC) as an innovative program for the mathematics training of prospective elenientary school teachers (PSTs). Each unit iswritten in an activity format that involves the PST in doing mathematicswith an eye towardaiplication of that mathematics in the elementary school. This do ument is one of four units that are devoted tothe basic number wo k in the elementary school. In addition to an introduction to the unit, the text has sections on the conceptual development of nultiplication
    [Show full text]
  • Algebraic Division by Zero Implemented As Quasigeometric Multiplication by Infinity in Real and Complex Multispatial Hyperspaces
    Available online at www.worldscientificnews.com WSN 92(2) (2018) 171-197 EISSN 2392-2192 Algebraic division by zero implemented as quasigeometric multiplication by infinity in real and complex multispatial hyperspaces Jakub Czajko Science/Mathematics Education Department, Southern University and A&M College, Baton Rouge, LA 70813, USA E-mail address: [email protected] ABSTRACT An unrestricted division by zero implemented as an algebraic multiplication by infinity is feasible within a multispatial hyperspace comprising several quasigeometric spaces. Keywords: Division by zero, infinity, multispatiality, multispatial uncertainty principle 1. INTRODUCTION Numbers used to be identified with their values. Yet complex numbers have two distinct single-number values: modulus/length and angle/phase, which can vary independently of each other. Since values are attributes of the algebraic entities called numbers, we need yet another way to define these entities and establish a basis that specifies their attributes. In an operational sense a number can be defined as the outcome of an algebraic operation. We must know the space where the numbers reside and the basis in which they are represented. Since division is inverse of multiplication, then reciprocal/contragradient basis can be used to represent inverse numbers for division [1]. Note that dual space, as conjugate space [2] is a space of functionals defined on elements of the primary space [3-5]. Although dual geometries are identical as sets, their geometrical structures are different [6] for duality can ( Received 18 December 2017; Accepted 03 January 2018; Date of Publication 04 January 2018 ) World Scientific News 92(2) (2018) 171-197 form anti-isomorphism or inverse isomorphism [7].
    [Show full text]