Lecture 7: Joint Distributions and the Law of Large Numbers E(X ) = P Var(X ) = P(1 − P)
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Reliable Reasoning”
Abstracta SPECIAL ISSUE III, pp. 10 – 17, 2009 COMMENTS ON HARMAN AND KULKARNI’S “RELIABLE REASONING” Glenn Shafer Gil Harman and Sanjeev Kulkarni have written an enjoyable and informative book that makes Vladimir Vapnik’s ideas accessible to a wide audience and explores their relevance to the philosophy of induction and reliable reasoning. The undertaking is important, and the execution is laudable. Vapnik’s work with Alexey Chervonenkis on statistical classification, carried out in the Soviet Union in the 1960s and 1970s, became popular in computer science in the 1990s, partly as the result of Vapnik’s books in English. Vapnik’s statistical learning theory and the statistical methods he calls support vector machines now dominate machine learning, the branch of computer science concerned with statistical prediction, and recently (largely after Harman and Kulkarni completed their book) these ideas have also become well known among mathematical statisticians. A century ago, when the academic world was smaller and less specialized, philosophers, mathematicians, and scientists interested in probability, induction, and scientific methodology talked with each other more than they do now. Keynes studied Bortkiewicz, Kolmogorov studied von Mises, Le Dantec debated Borel, and Fisher debated Jeffreys. Today, debate about probability and induction is mostly conducted within more homogeneous circles, intellectual communities that sometimes cross the boundaries of academic disciplines but overlap less in their discourse than in their membership. Philosophy of science, cognitive science, and machine learning are three of these communities. The greatest virtue of this book is that it makes ideas from these three communities confront each other. In particular, it looks at how Vapnik’s ideas in machine learning can answer or dissolve questions and puzzles that have been posed by philosophers. -

18.600: Lecture 31 .1In Strong Law of Large Numbers and Jensen's
18.600: Lecture 31 Strong law of large numbers and Jensen's inequality Scott Sheffield MIT Outline A story about Pedro Strong law of large numbers Jensen's inequality Outline A story about Pedro Strong law of large numbers Jensen's inequality I One possibility: put the entire sum in government insured interest-bearing savings account. He considers this completely risk free. The (post-tax) interest rate equals the inflation rate, so the real value of his savings is guaranteed not to change. I Riskier possibility: put sum in investment where every month real value goes up 15 percent with probability :53 and down 15 percent with probability :47 (independently of everything else). I How much does Pedro make in expectation over 10 years with risky approach? 100 years? Pedro's hopes and dreams I Pedro is considering two ways to invest his life savings. I Riskier possibility: put sum in investment where every month real value goes up 15 percent with probability :53 and down 15 percent with probability :47 (independently of everything else). I How much does Pedro make in expectation over 10 years with risky approach? 100 years? Pedro's hopes and dreams I Pedro is considering two ways to invest his life savings. I One possibility: put the entire sum in government insured interest-bearing savings account. He considers this completely risk free. The (post-tax) interest rate equals the inflation rate, so the real value of his savings is guaranteed not to change. I How much does Pedro make in expectation over 10 years with risky approach? 100 years? Pedro's hopes and dreams I Pedro is considering two ways to invest his life savings. -

Stochastic Models Laws of Large Numbers and Functional Central
This article was downloaded by: [Stanford University] On: 20 July 2010 Access details: Access Details: [subscription number 731837804] Publisher Taylor & Francis Informa Ltd Registered in England and Wales Registered Number: 1072954 Registered office: Mortimer House, 37- 41 Mortimer Street, London W1T 3JH, UK Stochastic Models Publication details, including instructions for authors and subscription information: http://www.informaworld.com/smpp/title~content=t713597301 Laws of Large Numbers and Functional Central Limit Theorems for Generalized Semi-Markov Processes Peter W. Glynna; Peter J. Haasb a Department of Management Science and Engineering, Stanford University, Stanford, California, USA b IBM Almaden Research Center, San Jose, California, USA To cite this Article Glynn, Peter W. and Haas, Peter J.(2006) 'Laws of Large Numbers and Functional Central Limit Theorems for Generalized Semi-Markov Processes', Stochastic Models, 22: 2, 201 — 231 To link to this Article: DOI: 10.1080/15326340600648997 URL: http://dx.doi.org/10.1080/15326340600648997 PLEASE SCROLL DOWN FOR ARTICLE Full terms and conditions of use: http://www.informaworld.com/terms-and-conditions-of-access.pdf This article may be used for research, teaching and private study purposes. Any substantial or systematic reproduction, re-distribution, re-selling, loan or sub-licensing, systematic supply or distribution in any form to anyone is expressly forbidden. The publisher does not give any warranty express or implied or make any representation that the contents will be complete or accurate or up to date. The accuracy of any instructions, formulae and drug doses should be independently verified with primary sources. The publisher shall not be liable for any loss, actions, claims, proceedings, demand or costs or damages whatsoever or howsoever caused arising directly or indirectly in connection with or arising out of the use of this material. -

On the Law of the Iterated Logarithm for L-Statistics Without Variance
Bulletin of the Institute of Mathematics Academia Sinica (New Series) Vol. 3 (2008), No. 3, pp. 417-432 ON THE LAW OF THE ITERATED LOGARITHM FOR L-STATISTICS WITHOUT VARIANCE BY DELI LI, DONG LIU AND ANDREW ROSALSKY Abstract Let {X, Xn; n ≥ 1} be a sequence of i.i.d. random vari- ables with distribution function F (x). For each positive inte- ger n, let X1:n ≤ X2:n ≤ ··· ≤ Xn:n be the order statistics of X1, X2, · · · , Xn. Let H(·) be a real Borel-measurable function de- fined on R such that E|H(X)| < ∞ and let J(·) be a Lipschitz function of order one defined on [0, 1]. Write µ = µ(F,J,H) = ← 1 n i E L : (J(U)H(F (U))) and n(F,J,H) = n Pi=1 J n H(Xi n), n ≥ 1, where U is a random variable with the uniform (0, 1) dis- ← tribution and F (t) = inf{x; F (x) ≥ t}, 0 <t< 1. In this note, the Chung-Smirnov LIL for empirical processes and the Einmahl- Li LIL for partial sums of i.i.d. random variables without variance are used to establish necessary and sufficient conditions for having L with probability 1: 0 < lim supn→∞ pn/ϕ(n) | n(F,J,H) − µ| < ∞, where ϕ(·) is from a suitable subclass of the positive, non- decreasing, and slowly varying functions defined on [0, ∞). The almost sure value of the limsup is identified under suitable con- ditions. Specializing our result to ϕ(x) = 2(log log x)p,p > 1 and to ϕ(x) = 2(log x)r,r > 0, we obtain an analog of the Hartman- Wintner-Strassen LIL for L-statistics in the infinite variance case. -

The Law of Large Numbers and the Monte-Carlo Method
Lecture 17: The Law of Large Numbers and the Monte-Carlo method The Law of Large numbers Suppose we perform an experiment and a measurement encoded in the random variable X and that we repeat this experiment n times each time in the same conditions and each time independently of each other. We thus obtain n independent copies of the random variable X which we denote X1;X2; ··· ;Xn Such a collection of random variable is called a IID sequence of random variables where IID stands for independent and identically distributed. This means that the random variables Xi have the same probability distribution. In particular they have all the same means and variance 2 E[Xi] = µ ; var(Xi) = σ ; i = 1; 2; ··· ; n Each time we perform the experiment n tiimes, the Xi provides a (random) measurement and if the average value X1 + ··· + Xn n is called the empirical average. The Law of Large Numbers states for large n the empirical average is very close to the expected value µ with very high probability Theorem 1. Let X1; ··· ;Xn IID random variables with E[Xi] = µ and var(Xi) for all i. Then we have 2 X1 + ··· Xn σ P − µ ≥ ≤ n n2 In particular the right hand side goes to 0 has n ! 1. Proof. The proof of the law of large numbers is a simple application from Chebyshev X1+···Xn inequality to the random variable n . Indeed by the properties of expectations we have X + ··· X 1 1 1 E 1 n = E [X + ··· X ] = (E [X ] + ··· E [X ]) = nµ = µ n n 1 n n 1 n n For the variance we use that the Xi are independent and so we have X + ··· X 1 1 σ2 var 1 n = var (X + ··· X ]) = (var(X ) + ··· + var(X )) = n n2 1 n n2 1 n n 1 By Chebyshev inequality we obtain then 2 X1 + ··· Xn σ P − µ ≥ ≤ n n2 Coin flip I: Suppose we flip a fair coin 100 times. -

Laws of Large Numbers in Stochastic Geometry with Statistical Applications
Bernoulli 13(4), 2007, 1124–1150 DOI: 10.3150/07-BEJ5167 Laws of large numbers in stochastic geometry with statistical applications MATHEW D. PENROSE Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, United Kingdom. E-mail: [email protected] Given n independent random marked d-vectors (points) Xi distributed with a common density, define the measure νn = i ξi, where ξi is a measure (not necessarily a point measure) which stabilizes; this means that ξi is determined by the (suitably rescaled) set of points near Xi. For d bounded test functions fPon R , we give weak and strong laws of large numbers for νn(f). The general results are applied to demonstrate that an unknown set A in d-space can be consistently estimated, given data on which of the points Xi lie in A, by the corresponding union of Voronoi cells, answering a question raised by Khmaladze and Toronjadze. Further applications are given concerning the Gamma statistic for estimating the variance in nonparametric regression. Keywords: law of large numbers; nearest neighbours; nonparametric regression; point process; random measure; stabilization; Voronoi coverage 1. Introduction Many interesting random variables in stochastic geometry arise as sums of contributions from each point of a point process Xn comprising n independent random d-vectors Xi, 1 ≤ i ≤ n, distributed with common density function. General limit theorems, including laws of large numbers (LLNs), central limit theorems and large deviation principles, have been obtained for such variables, based on a notion of stabilization (local dependence) of the contributions; see [16, 17, 18, 20]. -
STA111 - Lecture 8 Law of Large Numbers, Central Limit Theorem
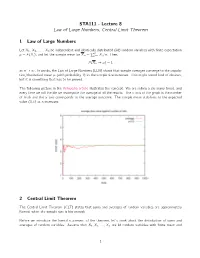
STA111 - Lecture 8 Law of Large Numbers, Central Limit Theorem 1 Law of Large Numbers Let X1, X2, ... , Xn be independent and identically distributed (iid) random variables with finite expectation Pn µ = E(Xi ), and let the sample mean be Xn = i=1 Xi =n. Then, P (Xn ! µ) = 1 as n ! 1. In words, the Law of Large Numbers (LLN) shows that sample averages converge to the popula- tion/theoretical mean µ (with probability 1) as the sample size increases. This might sound kind of obvious, but it is something that has to be proved. The following picture in the Wikipedia article illustrates the concept. We are rolling a die many times, and every time we roll the die we recompute the average of all the results. The x-axis of the graph is the number of trials and the y-axis corresponds to the average outcome. The sample mean stabilizes to the expected value (3.5) as n increases: 2 Central Limit Theorem The Central Limit Theorem (CLT) states that sums and averages of random variables are approximately Normal when the sample size is big enough. Before we introduce the formal statement of the theorem, let’s think about the distribution of sums and averages of random variables. Assume that X1;X2; ::: ; Xn are iid random variables with finite mean and 1 2 variance µ = E(Xi ) and σ = V (X), and let Sn = X1 + X2 + ··· + Xn and Xn = Sn=n. Using properties of expectations and variances, E(Sn) = E(X1) + E(X2) + ··· + E(Xn) = nµ 2 V (Sn) = V (X1) + V (X2) + ··· + V (Xn) = nσ : and similarly for Xn: 1 1 E(X ) = (E(X ) + E(X ) + ··· + E(X )) = (µ + µ + ··· + µ) = µ n n 1 2 n n 1 1 V (X ) = (V (X ) + V (X ) + ··· + V (X )) = (σ2 + σ2 + ··· + σ2) = σ2=n; n n2 1 2 n n2 2 The variance of the sample mean V (Xn) = σ =n shrinks to zero as n ! 1, which makes intuitive sense: as we get more and more data, the sample mean will become more and more precise. -

Law of Large Numbers
CS 70 Discrete Mathematics and Probability Theory Fall 2009 Satish Rao, David Tse Lecture 17 I.I.D. Random Variables Estimating the bias of a coin Question: We want to estimate the proportion p of Democrats in the US population, by taking a small random sample. How large does our sample have to be to guarantee that our estimate will be within (say) 10% (in relative terms) of the true value with probability at least 0.95? This is perhaps the most basic statistical estimation problem, and shows up everywhere. We will develop a simple solution that uses only Chebyshev’s inequality. More refined methods can be used to get sharper results. Let’s denote the size of our sample by n (to be determined), and the number of Democrats in it by the random variable Sn. (The subscript n just reminds us that the r.v. depends on the size of the sample.) Then 1 our estimate will be the value An = n Sn. (Now as has often been the case, we will find it helpful to write Sn = X1 + X2 + ¢¢¢ + Xn, where Xi = 1 if person i in sample is a Democrat; 0 otherwise. Note that each Xi can be viewed as a coin toss, with Heads probability p (though of course we do not know the value of p!). And the coin tosses are independent.1 What is the expectation of our estimate? 1 1 1 E(An) = E( n Sn) = n E(X1 + X2 + ¢¢¢ + Xn) = n £ (np) = p: So for any value of n, our estimate will always have the correct expectation p. -

The Exact Law of Large Numbers for Independent Random Matching
NBER WORKING PAPER SERIES THE EXACT LAW OF LARGE NUMBERS FOR INDEPENDENT RANDOM MATCHING Darrell Duffie Yeneng Sun Working Paper 17280 http://www.nber.org/papers/w17280 NATIONAL BUREAU OF ECONOMIC RESEARCH 1050 Massachusetts Avenue Cambridge, MA 02138 August 2011 This work was presented as "Independent Random Matching" at the International Congress of Nonstandard Methods in Mathematics, Pisa, Italy, May 25-31, 2006, the conference on Random Matching and Network Formation, University of Kentucky in Lexington, USA, October 20-22, 2006, and the 1st PRIMA Congress, Sydney, Australia, July 6-10, 2009. We are grateful for helpful comments from an anonymous associate editor of this journal, two anonymous referees, and from Haifeng Fu, Xiang Sun, Pierre-Olivier Weill, Yongchao Zhang and Zhixiang Zhang. The views expressed herein are those of the authors and do not necessarily reflect the views of the National Bureau of Economic Research. NBER working papers are circulated for discussion and comment purposes. They have not been peer- reviewed or been subject to the review by the NBER Board of Directors that accompanies official NBER publications. © 2011 by Darrell Duffie and Yeneng Sun. All rights reserved. Short sections of text, not to exceed two paragraphs, may be quoted without explicit permission provided that full credit, including © notice, is given to the source. The Exact Law of Large Numbers for Independent Random Matching Darrell Duffie and Yeneng Sun NBER Working Paper No. 17280 August 2011 JEL No. C02,D83 ABSTRACT This paper provides a mathematical foundation for independent random matching of a large population, as widely used in the economics literature. -

Lecture 7 the Law of Large Numbers, the Central Limit Theorem, the Elements of Mathematical Statistics the Law of Large Numbers
Lecture 7 The Law of Large Numbers, The Central Limit Theorem, The Elements of Mathematical Statistics The Law of Large Numbers For many experiments and observations concerning natural phenomena one finds that performing the procedure twice under (what seem) identical conditions results in two different outcomes. Uncontrollable factors cause “random” variation. In practice one tries to overcome this as follows: the experiment is repeated a number of times and the results are averaged in some way. The Law of Large Numbers In the following, we will see why this works so well, using a model for repeated measurements. We view them as a sequence of independent random variables, each with the same unknown distribution. It is a probabilistic fact that from such a sequence—in principle—any feature of the distribution can be recovered. This is a consequence of the law of large numbers . The Law of Large Numbers Scientists and engineers involved in experimental work have known for centuries that more accurate answers are obtained when measurements or experiments are repeated a number of times and one averages the individual outcomes. The Law of Large Numbers We consider a sequence of random variables , , ,… . You should think of as the result of the ith repetition of a particular measurement or experiment. We confine ourselves to the situation where experimental conditions of subsequent experiments are identical, and the outcome of any one experiment does not influence the outcomes of others. The Law of Large Numbers Under those circumstances, the random variables of the sequence are independent, and all have the same distribution, and we therefore call , , ,… an independent and identically distributed sequence . -

Laws of Large Numbers
Laws of Large Numbers + Chebyshev’s Inequality: Let X be a random variable and a ∈ R . We assume X has density function fX . Then Z 2 2 E(X ) = x fX (x) dx ZR 2 ≥ x fX (x) dx |x|≥a Z 2 2 ≥ a fX (x) dx = a P(|X| ≥ a) . |x|≥a That is, we have proved 1 P(|X| ≥ a) ≤ E(X2). (1) a2 We can generalize this to any moment p > 0: Z p p E(|X| ) = |x| fX (x) dx ZR p ≥ |x| fX (x) dx |x|≥a Z p p ≥ a fX (x) dx = a P(|X| ≥ a) . |x|≥a That is, we have proved 1 P(|X| ≥ a) ≤ E(|X|p) (2) ap for any p = 1, 2,.... (Of course, this assumes that E(|X|p) < ∞ for otherwise the inequality would not be saying much!) Remark: We have proved (1) and (2) assuming X has a density func- tion fX . However, (almost) identical proofs show the same inequalities for X having a discrete distribution. Weak Law of Large Numbers: Let X1, X2,X3, ... be a sequence of independent random variables with common distribution function. Set 2 µ = E(Xj) and σ = Var(Xj). As usual we define Sn = X1 + X2 + ··· + Xn 1 and let S S∗ = n − µ. n n ∗ We apply Chebyshev’s inequality to the random variable Sn. A by now routine calculation gives σ2 E(S∗) = 0 and Var(S∗) = . n n n Then Chebyshev (1) says that for every ε > 0 1 P(|S∗| ≥ ε) ≤ Var(S∗). n ε2 n Writing this out explicitly: 2 X1 + X2 + ··· + Xn 1 σ P − µ ≥ ε ≤ . -

Randomness? What Randomness? Email
Randomness? What randomness? Klaas Landsmana Dedicated to Gerard ’t Hooft, on the 20th anniversary of his Nobel Prizeb Abstract This is a review of the issue of randomness in quantum mechanics, with special empha- sis on its ambiguity; for example, randomness has different antipodal relationships to determinism, computability, and compressibility. Following a (Wittgensteinian) philo- sophical discussion of randomness in general, I argue that deterministic interpretations of quantum mechanics (like Bohmian mechanics or ’t Hooft’s Cellular Automaton in- terpretation) are strictly speaking incompatible with the Born rule. I also stress the role of outliers, i.e. measurement outcomes that are not 1-random. Although these occur with low (or even zero) probability, their very existence implies that the no- signaling principle used in proofs of randomness of outcomes of quantum-mechanical measurements (and of the safety of quantum cryptography) should be reinterpreted statistically, like the second law of thermodynamics. In three appendices I discuss the Born rule and its status in both single and repeated experiments, review the notion of 1-randomness (or algorithmic randomness) that in various guises was investigated by Solomonoff, Kolmogorov, Chaitin, Martin-L¨of, Schnorr, and others, and treat Bell’s (1964) Theorem and the Free Will Theorem with their implications for randomness. Contents 1 Introduction 2 2 Randomness as a family resemblance 3 3 Randomness in quantum mechanics 8 4 Probabilistic preliminaries 11 5 Critical analysis and claims 13 A The Born rule revisited 18 B 1-Randomness 23 C Bell’s Theorem and Free Will Theorem 29 arXiv:1908.07068v2 [physics.hist-ph] 30 Nov 2019 References 32 aDepartment of Mathematics, Institute for Mathematics, Astrophysics, and Particle Physics (IMAPP), Faculty of Science, Radboud University, Nijmegen, The Netherlands, and Dutch Institute for Emergent Phenomena (DIEP), www.d-iep.org.