The Asymptotic Giant Branch and Eventually Be- Come Planetary Nebulae and White Dwarfs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2.5 Dimensional Radiative Transfer Modeling of Proto-Planetary Nebula Dust Shells with 2-DUST
PLANETARY NEBULAE: THEIR EVOLUTION AND ROLE IN THE UNIVERSE fA U Symposium, Vol. 209, 2003 S. Kwok, M. Dopita, and R. Sutherland, eds. 2.5 Dimensional Radiative Transfer Modeling of Proto-Planetary Nebula Dust Shells with 2-DUST Toshiya Ueta & Margaret Meixner Department of Astronomy, MC-221 , University of fllinois at Urbana-Champaign, Urbana, IL 61801, USA ueta@astro. uiuc.edu, [email protected]. edu Abstract. Our observing campaign of proto-planetary nebula (PPN) dust shells has shown that the structure formation in planetary nebu- lae (PNs) begins as early as the late asymptotic. giant branch (AGB) phase due to intrinsically axisymmetric superwind. We describe our latest numerical efforts with a multi-dimensional dust radiative transfer code, 2-DUST, in order to explain the apparent dichotomy of the PPN mor- phology at the mid-IR and optical, which originates most likely from the optical depth of the shell combined with the effect of inclination angle. 1. Axisymmetric PPN Shells and Single Density Distribution Model Since the PPN phase predates the period of final PN shaping due to interactions of the stellar winds, we can investigate the origin of the PN structure formation by observationally establishing the material distribution in the PPN shells, in which pristine fossil records of AGB mass loss histories are preserved in their benign circumstellar environment. Our mid-IR and optical imaging surveys of PPN candidates in the past several years (Meixner at al. 1999; Ueta et al. 2000) have revealed that (1) PPN shells are intrinsically axisymmetric most likely due to equatorially-enhanced superwind mass loss at the end of the AGB phase and (2) varying degrees of equatorial enhancement in superwind would result in different optical depths of the PPN shell, thereby heavily influencing the mid-IR and optical morphologies. -

Spectroscopic Analysis of Accretion/Ejection Signatures in the Herbig Ae/Be Stars HD 261941 and V590 Mon T Moura, S
Spectroscopic analysis of accretion/ejection signatures in the Herbig Ae/Be stars HD 261941 and V590 Mon T Moura, S. Alencar, A. Sousa, E. Alecian, Y. Lebreton To cite this version: T Moura, S. Alencar, A. Sousa, E. Alecian, Y. Lebreton. Spectroscopic analysis of accretion/ejection signatures in the Herbig Ae/Be stars HD 261941 and V590 Mon. Monthly Notices of the Royal Astronomical Society, Oxford University Press (OUP): Policy P - Oxford Open Option A, 2020, 494 (3), pp.3512-3535. 10.1093/mnras/staa695. hal-02523038 HAL Id: hal-02523038 https://hal.archives-ouvertes.fr/hal-02523038 Submitted on 16 May 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. MNRAS 000,1–24 (2019) Preprint 27 February 2020 Compiled using MNRAS LATEX style file v3.0 Spectroscopic analysis of accretion/ejection signatures in the Herbig Ae/Be stars HD 261941 and V590 Mon T. Moura1?, S. H. P. Alencar1, A. P. Sousa1;2, E. Alecian2, Y. Lebreton3;4 1Universidade Federal de Minas Gerais, Departamento de Física, Av. Antônio Carlos 6627, 31270-901, Brazil 2Univ. Grenoble Alpes, IPAG, F-38000 Grenoble, France 3LESIA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ. -

Planetary Nebulae Jacob Arnold AY230, Fall 2008
Jacob Arnold Planetary Nebulae Jacob Arnold AY230, Fall 2008 1 PNe Formation Low mass stars (less than 8 M) will travel through the asymptotic giant branch (AGB) of the familiar HR-diagram. During this stage of evolution, energy generation is primarily relegated to a shell of helium just outside of the carbon-oxygen core. This thin shell of fusing He cannot expand against the outer layer of the star, and rapidly heats up while also quickly exhausting its reserves and transferring its head outwards. When the He is depleted, Hydrogen burning begins in a shell just a little farther out. Over time, helium builds up again, and very abruptly begins burning, leading to a shell-helium-flash (thermal pulse). During the thermal-pulse AGB phase, this process repeats itself, leading to mass loss at the extended outer envelope of the star. The pulsations extend the outer layers of the star, causing the temperature to drop below the condensation temperature for grain formation (Zijlstra 2006). Grains are driven off the star by radiation pressure, bringing gas with them through collisions. The mass loss from pulsating AGB stars is oftentimes referred to as a wind. For AGB stars, the surface gravity of the star is quite low, and wind speeds of ~10 km/s are more than sufficient to drive off mass. At some point, a super wind develops that removes the envelope entirely, a phenomenon not yet fully understood (Bernard-Salas 2003). The central, primarily carbon-oxygen core is thus exposed. These cores can have temperatures in the hundreds of thousands of Kelvin, leading to a very strong ionizing source. -

X-Ray Sun SDO 4500 Angstroms: Photosphere
ASTR 8030/3600 Stellar Astrophysics X-ray Sun SDO 4500 Angstroms: photosphere T~5000K SDO 1600 Angstroms: upper photosphere T~5x104K SDO 304 Angstroms: chromosphere T~105K SDO 171 Angstroms: quiet corona T~6x105K SDO 211 Angstroms: active corona T~2x106K SDO 94 Angstroms: flaring regions T~6x106K SDO: dark plasma (3/27/2012) SDO: solar flare (4/16/2012) SDO: coronal mass ejection (7/2/2012) Aims of the course • Introduce the equations needed to model the internal structure of stars. • Overview of how basic stellar properties are observationally measured. • Study the microphysics relevant for stars: the equation of state, the opacity, nuclear reactions. • Examine the properties of simple models for stars and consider how real models are computed. • Survey (mostly qualitatively) how stars evolve, and the endpoints of stellar evolution. Stars are relatively simple physical systems Sound speed in the sun Problem of Stellar Structure We want to determine the structure (density, temperature, energy output, pressure as a function of radius) of an isolated mass M of gas with a given composition (e.g., H, He, etc.) Known: r Unknown: Mass Density + Temperature Composition Energy Pressure Simplifying assumptions 1. No rotation à spherical symmetry ✔ For sun: rotation period at surface ~ 1 month orbital period at surface ~ few hours 2. No magnetic fields ✔ For sun: magnetic field ~ 5G, ~ 1KG in sunspots equipartition field ~ 100 MG Some neutron stars have a large fraction of their energy in B fields 3. Static ✔ For sun: convection, but no large scale variability Not valid for forming stars, pulsating stars and dying stars. 4. -
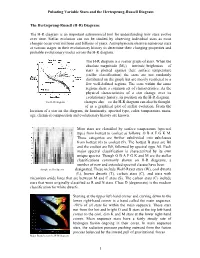
Plotting Variable Stars on the H-R Diagram Activity
Pulsating Variable Stars and the Hertzsprung-Russell Diagram The Hertzsprung-Russell (H-R) Diagram: The H-R diagram is an important astronomical tool for understanding how stars evolve over time. Stellar evolution can not be studied by observing individual stars as most changes occur over millions and billions of years. Astrophysicists observe numerous stars at various stages in their evolutionary history to determine their changing properties and probable evolutionary tracks across the H-R diagram. The H-R diagram is a scatter graph of stars. When the absolute magnitude (MV) – intrinsic brightness – of stars is plotted against their surface temperature (stellar classification) the stars are not randomly distributed on the graph but are mostly restricted to a few well-defined regions. The stars within the same regions share a common set of characteristics. As the physical characteristics of a star change over its evolutionary history, its position on the H-R diagram The H-R Diagram changes also – so the H-R diagram can also be thought of as a graphical plot of stellar evolution. From the location of a star on the diagram, its luminosity, spectral type, color, temperature, mass, age, chemical composition and evolutionary history are known. Most stars are classified by surface temperature (spectral type) from hottest to coolest as follows: O B A F G K M. These categories are further subdivided into subclasses from hottest (0) to coolest (9). The hottest B stars are B0 and the coolest are B9, followed by spectral type A0. Each major spectral classification is characterized by its own unique spectra. -

The Evolution of Helium White Dwarfs: Applications to Millisecond
Pulsar Astronomy — 2000 and Beyond ASP Conference Series, Vol. 3 × 108, 1999 M. Kramer, N. Wex, and R. Wielebinski, eds. The evolution of helium white dwarfs: Applications for millisecond pulsars T. Driebe and T. Bl¨ocker Max-Planck-Institut f¨ur Radioastronomie, Bonn, Germany D. Sch¨onberner Astrophysikalisches Institut Potsdam, Potsdam, Germany 1. White Dwarf Evolution Low-mass white dwarfs with helium cores (He-WDs) are known to result from mass loss and/or exchange events in binary systems where the donor is a low mass star evolving along the red giant branch (RGB). Therefore, He-WDs are common components in binary systems with either two white dwarfs or with a white dwarf and a millisecond pulsar (MSP). If the cooling behaviour of He- WDs is known from theoretical studies (see Driebe et al. 1998, and references therein) the ages of MSP systems can be calculated independently of the pulsar properties provided the He-WD mass is known from spectroscopy. Driebe et al. (1998, 1999) investigated the evolution of He-WDs in the mass range 0.18 < MWD/M⊙ < 0.45 using the code of Bl¨ocker (1995). The evolution of a 1 M⊙-model was calculated up to the tip of the RGB. High mass loss termi- nated the RGB evolution at appropriate positions depending on the desired final white dwarf mass. When the model started to leave the RGB, mass loss was virtually switched off and the models evolved towards the white dwarf cooling branch. The applied procedure mimicks the mass transfer in binary systems. Contrary to the more massive C/O-WDs (MWD ∼> 0.5 M⊙, carbon/oxygen core), whose progenitors have also evolved through the asymptotic giant branch phase, He-WDs can continue to burn hydrogen via the pp cycle along the cooling branch arXiv:astro-ph/9910230v1 13 Oct 1999 down to very low effective temperatures, resulting in cooling ages of the order of Gyr, i. -

• Classifying Stars: HR Diagram • Luminosity, Radius, and Temperature • “Vogt-Russell” Theorem • Main Sequence • Evolution on the HR Diagram
Stars • Classifying stars: HR diagram • Luminosity, radius, and temperature • “Vogt-Russell” theorem • Main sequence • Evolution on the HR diagram Classifying stars • We now have two properties of stars that we can measure: – Luminosity – Color/surface temperature • Using these two characteristics has proved extraordinarily effective in understanding the properties of stars – the Hertzsprung- Russell (HR) diagram If we plot lots of stars on the HR diagram, they fall into groups These groups indicate types of stars, or stages in the evolution of stars Luminosity classes • Class Ia,b : Supergiant • Class II: Bright giant • Class III: Giant • Class IV: Sub-giant • Class V: Dwarf The Sun is a G2 V star Luminosity versus radius and temperature A B R = R R = 2 RSun Sun T = T T = TSun Sun Which star is more luminous? Luminosity versus radius and temperature A B R = R R = 2 RSun Sun T = T T = TSun Sun • Each cm2 of each surface emits the same amount of radiation. • The larger stars emits more radiation because it has a larger surface. It emits 4 times as much radiation. Luminosity versus radius and temperature A1 B R = RSun R = RSun T = TSun T = 2TSun Which star is more luminous? The hotter star is more luminous. Luminosity varies as T4 (Stefan-Boltzmann Law) Luminosity Law 2 4 LA = RATA 2 4 LB RBTB 1 2 If star A is 2 times as hot as star B, and the same radius, then it will be 24 = 16 times as luminous. From a star's luminosity and temperature, we can calculate the radius. -

Stars IV Stellar Evolution Attendance Quiz
Stars IV Stellar Evolution Attendance Quiz Are you here today? Here! (a) yes (b) no (c) my views are evolving on the subject Today’s Topics Stellar Evolution • An alien visits Earth for a day • A star’s mass controls its fate • Low-mass stellar evolution (M < 2 M) • Intermediate and high-mass stellar evolution (2 M < M < 8 M; M > 8 M) • Novae, Type I Supernovae, Type II Supernovae An Alien Visits for a Day • Suppose an alien visited the Earth for a day • What would it make of humans? • It might think that there were 4 separate species • A small creature that makes a lot of noise and leaks liquids • A somewhat larger, very energetic creature • A large, slow-witted creature • A smaller, wrinkled creature • Or, it might decide that there is one species and that these different creatures form an evolutionary sequence (baby, child, adult, old person) Stellar Evolution • Astronomers study stars in much the same way • Stars come in many varieties, and change over times much longer than a human lifetime (with some spectacular exceptions!) • How do we know they evolve? • We study stellar properties, and use our knowledge of physics to construct models and draw conclusions about stars that lead to an evolutionary sequence • As with stellar structure, the mass of a star determines its evolution and eventual fate A Star’s Mass Determines its Fate • How does mass control a star’s evolution and fate? • A main sequence star with higher mass has • Higher central pressure • Higher fusion rate • Higher luminosity • Shorter main sequence lifetime • Larger -

Stellar Structure and Evolution
Lecture Notes on Stellar Structure and Evolution Jørgen Christensen-Dalsgaard Institut for Fysik og Astronomi, Aarhus Universitet Sixth Edition Fourth Printing March 2008 ii Preface The present notes grew out of an introductory course in stellar evolution which I have given for several years to third-year undergraduate students in physics at the University of Aarhus. The goal of the course and the notes is to show how many aspects of stellar evolution can be understood relatively simply in terms of basic physics. Apart from the intrinsic interest of the topic, the value of such a course is that it provides an illustration (within the syllabus in Aarhus, almost the first illustration) of the application of physics to “the real world” outside the laboratory. I am grateful to the students who have followed the course over the years, and to my colleague J. Madsen who has taken part in giving it, for their comments and advice; indeed, their insistent urging that I replace by a more coherent set of notes the textbook, supplemented by extensive commentary and additional notes, which was originally used in the course, is directly responsible for the existence of these notes. Additional input was provided by the students who suffered through the first edition of the notes in the Autumn of 1990. I hope that this will be a continuing process; further comments, corrections and suggestions for improvements are most welcome. I thank N. Grevesse for providing the data in Figure 14.1, and P. E. Nissen for helpful suggestions for other figures, as well as for reading and commenting on an early version of the manuscript. -

Spring Semester 2010 Exam 3 – Answers a Planetary Nebula Is A
ASTR 1120H – Spring Semester 2010 Exam 3 – Answers PART I (70 points total) – 14 short answer questions (5 points each): 1. What is a planetary nebula? How long can a planetary nebula be observed? A planetary nebula is a luminous shell of gas ejected from an old, low- mass star. It can be observed for approximately 50,000 years; after that it its gases will have ceased to glow and it will simply fade from view. 2. What is a white dwarf star? How does a white dwarf change over time? A white dwarf star is a low-mass star that has exhausted all its nuclear fuel and contracted to a size roughly equal to the size of the Earth. It is supported against further contraction by electron degeneracy pressure. As a white dwarf ages, though, it will radiate, thereby cooling and getting less luminous. 3. Name at least three differences between Type Ia supernovae and Type II supernovae. Type Ia SN are intrinsically brighter than Type II SN. Type II SN show hydrogen emission lines; Type Ia SN don't. Type II SN are thought to arise from core collapse of a single, massive star. Type Ia SN are thought to arise from accretion from a binary companion onto a white dwarf star, pushing the white dwarf beyond the Chandrasekhar limit and causing a nuclear detonation that destroys the white dwarf. 4. Why was SN 1987A so important? SN 1987A was the first naked-eye SN in almost 400 years. It was the first SN for which a precursor star could be identified. -

Part V Stellar Spectroscopy
Part V Stellar spectroscopy 53 Chapter 10 Classification of stellar spectra Goal-of-the-Day To classify a sample of stars using a number of temperature-sensitive spectral lines. 10.1 The concept of spectral classification Early in the 19th century, the German physicist Joseph von Fraunhofer observed the solar spectrum and realised that there was a clear pattern of absorption lines superimposed on the continuum. By the end of that century, astronomers were able to examine the spectra of stars in large numbers and realised that stars could be divided into groups according to the general appearance of their spectra. Classification schemes were developed that grouped together stars depending on the prominence of particular spectral lines: hydrogen lines, helium lines and lines of some metallic ions. Astronomers at Harvard Observatory further developed and refined these early classification schemes and spectral types were defined to reflect a smooth change in the strength of representative spectral lines. The order of the spectral classes became O, B, A, F, G, K, and M; even though these letter designations no longer have specific meaning the names are still in use today. Each spectral class is divided into ten sub-classes, so that for instance a B0 star follows an O9 star. This classification scheme was based simply on the appearance of the spectra and the physical reason underlying these properties was not understood until the 1930s. Even though there are some genuine differences in chemical composition between stars, the main property that determines the observed spectrum of a star is its effective temperature. -

The Deaths of Stars
The Deaths of Stars 1 Guiding Questions 1. What kinds of nuclear reactions occur within a star like the Sun as it ages? 2. Where did the carbon atoms in our bodies come from? 3. What is a planetary nebula, and what does it have to do with planets? 4. What is a white dwarf star? 5. Why do high-mass stars go through more evolutionary stages than low-mass stars? 6. What happens within a high-mass star to turn it into a supernova? 7. Why was SN 1987A an unusual supernova? 8. What was learned by detecting neutrinos from SN 1987A? 9. How can a white dwarf star give rise to a type of supernova? 10.What remains after a supernova explosion? 2 Pathways of Stellar Evolution GOOD TO KNOW 3 Low-mass stars go through two distinct red-giant stages • A low-mass star becomes – a red giant when shell hydrogen fusion begins – a horizontal-branch star when core helium fusion begins – an asymptotic giant branch (AGB) star when the helium in the core is exhausted and shell helium fusion begins 4 5 6 7 Bringing the products of nuclear fusion to a giant star’s surface • As a low-mass star ages, convection occurs over a larger portion of its volume • This takes heavy elements formed in the star’s interior and distributes them throughout the star 8 9 Low-mass stars die by gently ejecting their outer layers, creating planetary nebulae • Helium shell flashes in an old, low-mass star produce thermal pulses during which more than half the star’s mass may be ejected into space • This exposes the hot carbon-oxygen core of the star • Ultraviolet radiation from the exposed