Getting It Right

Total Page：16

File Type：pdf, Size：1020Kb

by B S Beevers The results so far may be put into a table as follows: Number of Sides 3 4 5 6 7 8 9 10 11 12 Number of rt. angles 1 4 3 5 5 6 7 7 8 9 etting it right Now polygons with 3, 4 and 5 sides are special cases, after which there appears to be a clear pattern for the maximum A familiar investigation is to find the maximum numbers of number of right angles. interior angles of a polygon which can be right angles. This may be investigated by an able pupil as follows: Analytical Approach A triangle can have one right angle. A quadrilateral can have four right angles. For a polygon with n sides, sum of interior angles = 180n - 360 degrees. Pentagon Suppose it has p right angles. Number of degrees remaining for other angles = 180n - 360 Sum of Interior Angles = 540'. - 90p. Four right angles would leave 180', which is impossible. Average size of remaining angles must be less than 360'. So a pentagon has a maximum of three right angles, as shown. Hence: 180n - 360 - 90p < 360 n-p Hence 180n - 360 - 90p < 360n - 360p - 270p < 180n + 360 1 3 Hexagon -p< - (2n + 4) n = 3, 4 and 5 are special cases. Sum of Angles = 720'. For n > 5, the maximum number of right-angles is the 5 right angles = 450', leaving 270'. largest integer less than (2n + 4) So a hexagon can have 5 right-angles, as shown. Note that p cannot equal (2n + 4) or the average remaining angle would equal 360. Here is a table of values ofp for n > 5. n 6 7 8 9 10 11 12 13 1 2 10 (2n 3 + 4)3 51 3 6 623 71 38 8 93 10 p5 5 6 7 7 8 9 9 We can obtain a formula for three cases as follows: 1 Let q = (2n + 4) 3 Heptagon 1 1 Sum of Angles = 900'. If n = 3m then q (6m + 4) = 2m+ 1 +- So p = 2m + 1 6 right angles = 540', leaving 360', which is impossible. Sop= 2m + 1 So maximum number is 5. Octagon 1 Sum of angles = 1080'. If n = 3m+ 1then q=- 3 (6m + 6) = 2m + 2 7 right angles = 630', leaving 450'. So p = 2m + 1 6 right angles = 540', leaving 540'. So an octagon can have 6 right angles. 1 2 Nonagon If n = So3m +p 2 =then 2m q--3 +(6m 2 + 8) = 2m + 2 + - Sum of angles = 1260'. Sop= 2m + 2 8 right angles = 720', leaving 540'. 7 right angles = 630', leaving 630'. Conclusions: If n = 3m then p = 2m + 1 Since 630/2 = 315 < 360, this is alright. If n = 3m + 1then p = 2m + 1 So maximum number of right angles is 7, as shown. If n = 3m + 2 then p = 2m + 2 Example: Let n = 20 Then 20= 3 x 6 + 2, so m = 6 Hencep 2 x 6 + 2 = 14. So the maximum number of right angles for a 20 sided polygon is 14. - Address 18 Welburn Avenue, Leeds LS16 5HJ. Mathematics in School, March 1996 37.

Copy Link

Recommended publications

PERFORMED IDENTITIES: HEAVY METAL MUSICIANS BETWEEN 1984 and 1991 Bradley C. Klypchak a Dissertation Submitted to the Graduate
PERFORMED IDENTITIES: HEAVY METAL MUSICIANS BETWEEN 1984 AND 1991 Bradley C. Klypchak A Dissertation Submitted to the Graduate College of Bowling Green State University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY May 2007 Committee: Dr. Jeffrey A. Brown, Advisor Dr. John Makay Graduate Faculty Representative Dr. Ron E. Shields Dr. Don McQuarie © 2007 Bradley C. Klypchak All Rights Reserved iii ABSTRACT Dr. Jeffrey A. Brown, Advisor Between 1984 and 1991, heavy metal became one of the most publicly popular and commercially successful rock music subgenres. The focus of this dissertation is to explore the following research questions: How did the subculture of heavy metal music between 1984 and 1991 evolve and what meanings can be derived from this ongoing process? How did the contextual circumstances surrounding heavy metal music during this period impact the performative choices exhibited by artists, and from a position of retrospection, what lasting significance does this particular era of heavy metal merit today? A textual analysis of metal- related materials fostered the development of themes relating to the selective choices made and performances enacted by metal artists. These themes were then considered in terms of gender, sexuality, race, and age constructions as well as the ongoing negotiations of the metal artist within multiple performative realms. Occurring at the juncture of art and commerce, heavy metal music is a purposeful construction. Metal musicians made performative choices for serving particular aims, be it fame, wealth, or art. These same individuals worked within a greater system of influence. Metal bands were the contracted employees of record labels whose own corporate aims needed to be recognized.
[Show full text]
And Twelve-Pointed Star Polygon Design of the Tashkent Scrolls
Bridges 2011: Mathematics, Music, Art, Architecture, Culture A Nine- and Twelve-Pointed Star Polygon Design of the Tashkent Scrolls B. Lynn Bodner Mathematics Department Cedar Avenue Monmouth University West Long Branch, New Jersey, 07764, USA E-mail: [email protected] Abstract In this paper we will explore one of the Tashkent Scrolls’ repeat units, that, when replicated using symmetry operations, creates an overall pattern consisting of “nearly regular” nine-pointed, regular twelve-pointed and irregularly-shaped pentagonal star polygons. We seek to determine how the original designer of this pattern may have determined, without mensuration, the proportion and placement of the star polygons comprising the design. We will do this by proposing a plausible Euclidean “point-joining” compass-and-straightedge reconstruction. Introduction The Tashkent Scrolls (so named because they are housed in Tashkent at the Institute of Oriental Studies at the Academy of Sciences) consist of fragments of architectural sketches attributed to an Uzbek master builder or a guild of architects practicing in 16 th century Bukhara [1, p. 7]. The sketch from the Tashkent Scrolls that we will explore shows only a small portion, or the repeat unit , of a nine- and twelve-pointed star polygon design. It is contained within a rectangle and must be reflected across the boundaries of this rectangle to achieve the entire pattern. This drawing, which for the remainder of this paper we will refer to as “T9N12,” is similar to many of the 114 Islamic architectural and ornamental design sketches found in the much larger, older and better preserved Topkapı Scroll, a 96-foot-long architectural scroll housed at the Topkapı Palace Museum Library in Istanbul.
[Show full text]
Islamic Geometric Ornaments in Istanbul
►SKETCH 2 CONSTRUCTIONS OF REGULAR POLYGONS Regular polygons are the base elements for constructing the majority of Islamic geometric ornaments. Of course, in Islamic art there are geometric ornaments that may have different genesis, but those that can be created from regular polygons are the most frequently seen in Istanbul. We can also notice that many of the Islamic geometric ornaments can be recreated using rectangular grids like the ornament in our first example. Sometimes methods using rectangular grids are much simpler than those based or regular polygons. Therefore, we should not omit these methods. However, because methods for constructing geometric ornaments based on regular polygons are the most popular, we will spend relatively more time explor- ing them. Before, we start developing some concrete constructions it would be worthwhile to look into a few issues of a general nature. As we have no- ticed while developing construction of the ornament from the floor in the Sultan Ahmed Mosque, these constructions are not always simple, and in order to create them we need some knowledge of elementary geometry. On the other hand, computer programs for geometry or for computer graphics can give us a number of simpler ways to develop geometric fig- ures. Some of them may not require any knowledge of geometry. For ex- ample, we can create a regular polygon with any number of sides by rotat- ing a point around another point by using rotations 360/n degrees. This is a very simple task if we use a computer program and the only knowledge of geometry we need here is that the full angle is 360 degrees.
[Show full text]
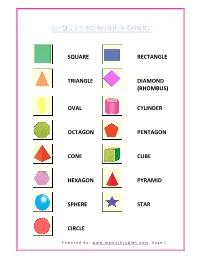
Square Rectangle Triangle Diamond (Rhombus) Oval Cylinder Octagon Pentagon Cone Cube Hexagon Pyramid Sphere Star Circle
SQUARE RECTANGLE TRIANGLE DIAMOND (RHOMBUS) OVAL CYLINDER OCTAGON PENTAGON CONE CUBE HEXAGON PYRAMID SPHERE STAR CIRCLE Powered by: www.mymathtables.com Page 1 what is Rectangle? • A rectangle is a four-sided flat shape where every angle is a right angle (90°). means "right angle" and show equal sides. what is Triangle? • A triangle is a polygon with three edges and three vertices. what is Octagon? • An octagon (eight angles) is an eight-sided polygon or eight-gon. what is Hexagon? • a hexagon is a six-sided polygon or six-gon. The total of the internal angles of any hexagon is 720°. what is Pentagon? • a plane figure with five straight sides and five angles. what is Square? • a plane figure with four equal straight sides and four right angles. • every angle is a right angle (90°) means "right ang le" show equal sides. what is Rhombus? • is a flat shape with four equal straight sides. A rhombus looks like a diamond. All sides have equal length. Opposite sides are parallel, and opposite angles are equal what is Oval? • Many distinct curves are commonly called ovals or are said to have an "oval shape". • Generally, to be called an oval, a plane curve should resemble the outline of an egg or an ellipse. Powered by: www.mymathtables.com Page 2 What is Cube? • Six equal square faces.tweleve edges and eight vertices • the angle between two adjacent faces is ninety. what is Sphere? • no faces,sides,vertices • All points are located at the same distance from the center. what is Cylinder? • two circular faces that are congruent and parallel • faces connected by a curved surface.
[Show full text]
Framing Cyclic Revolutionary Emergence of Opposing Symbols of Identity Eppur Si Muove: Biomimetic Embedding of N-Tuple Helices in Spherical Polyhedra - /
Alternative view of segmented documents via Kairos 23 October 2017 | Draft Framing Cyclic Revolutionary Emergence of Opposing Symbols of Identity Eppur si muove: Biomimetic embedding of N-tuple helices in spherical polyhedra - / - Introduction Symbolic stars vs Strategic pillars; Polyhedra vs Helices; Logic vs Comprehension? Dynamic bonding patterns in n-tuple helices engendering n-fold rotating symbols Embedding the triple helix in a spherical octahedron Embedding the quadruple helix in a spherical cube Embedding the quintuple helix in a spherical dodecahedron and a Pentagramma Mirificum Embedding six-fold, eight-fold and ten-fold helices in appropriately encircled polyhedra Embedding twelve-fold, eleven-fold, nine-fold and seven-fold helices in appropriately encircled polyhedra Neglected recognition of logical patterns -- especially of opposition Dynamic relationship between polyhedra engendered by circles -- variously implying forms of unity Symbol rotation as dynamic essential to engaging with value-inversion References Introduction The contrast to the geocentric model of the solar system was framed by the Italian mathematician, physicist and philosopher Galileo Galilei (1564-1642). His much-cited phrase, " And yet it moves" (E pur si muove or Eppur si muove) was allegedly pronounced in 1633 when he was forced to recant his claims that the Earth moves around the immovable Sun rather than the converse -- known as the Galileo affair. Such a shift in perspective might usefully inspire the recognition that the stasis attributed so widely to logos and other much-valued cultural and heraldic symbols obscures the manner in which they imply a fundamental cognitive dynamic. Cultural symbols fundamental to the identity of a group might then be understood as variously moving and transforming in ways which currently elude comprehension.
[Show full text]
Applying the Polygon Angle
POLYGONS 8.1.1 – 8.1.5 After studying triangles and quadrilaterals, students now extend their study to all polygons. A polygon is a closed, two-dimensional figure made of three or more non- intersecting straight line segments connected end-to-end. Using the fact that the sum of the measures of the angles in a triangle is 180°, students learn a method to determine the sum of the measures of the interior angles of any polygon. Next they explore the sum of the measures of the exterior angles of a polygon. Finally they use the information about the angles of polygons along with their Triangle Toolkits to find the areas of regular polygons. See the Math Notes boxes in Lessons 8.1.1, 8.1.5, and 8.3.1. Example 1 4x + 7 3x + 1 x + 1 The figure at right is a hexagon. What is the sum of the measures of the interior angles of a hexagon? Explain how you know. Then write an equation and solve for x. 2x 3x – 5 5x – 4 One way to find the sum of the interior angles of the 9 hexagon is to divide the figure into triangles. There are 11 several different ways to do this, but keep in mind that we 8 are trying to add the interior angles at the vertices. One 6 12 way to divide the hexagon into triangles is to draw in all of 10 the diagonals from a single vertex, as shown at right. 7 Doing this forms four triangles, each with angle measures 5 4 3 1 summing to 180°.
[Show full text]
Polygon Review and Puzzlers in the Above, Those Are Names to the Polygons: Fill in the Blank Parts. Names: Number of Sides
Polygon review and puzzlers ÆReview to the classification of polygons: Is it a Polygon? Polygons are 2-dimensional shapes. They are made of straight lines, and the shape is "closed" (all the lines connect up). Polygon Not a Polygon Not a Polygon (straight sides) (has a curve) (open, not closed) Regular polygons have equal length sides and equal interior angles. Polygons are named according to their number of sides. Name of Degree of Degree of triangle total angles regular angles Triangle 180 60 In the above, those are names to the polygons: Quadrilateral 360 90 fill in the blank parts. Pentagon Hexagon Heptagon 900 129 Names: number of sides: Octagon Nonagon hendecagon, 11 dodecagon, _____________ Decagon 1440 144 tetradecagon, 13 hexadecagon, 15 Do you see a pattern in the calculation of the heptadecagon, _____________ total degree of angles of the polygon? octadecagon, _____________ --- (n -2) x 180° enneadecagon, _____________ icosagon 20 pentadecagon, _____________ These summation of angles rules, also apply to the irregular polygons, try it out yourself !!! A point where two or more straight lines meet. Corner. Example: a corner of a polygon (2D) or of a polyhedron (3D) as shown. The plural of vertex is "vertices” Test them out yourself, by drawing diagonals on the polygons. Here are some fun polygon riddles; could you come up with the answer? Geometry polygon riddles I: My first is in shape and also in space; My second is in line and also in place; My third is in point and also in line; My fourth in operation but not in sign; My fifth is in angle but not in degree; My sixth is in glide but not symmetry; Geometry polygon riddles II: I am a polygon all my angles have the same measure all my five sides have the same measure, what general shape am I? Geometry polygon riddles III: I am a polygon.
[Show full text]
Interior and Exterior Angles of Polygons 2A
Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org G.CO.C.11: Interior and Exterior Angles of Polygons 2a 1 Which type of figure is shown in the accompanying 5 In the diagram below of regular pentagon ABCDE, diagram? EB is drawn. 1) hexagon 2) octagon 3) pentagon 4) quadrilateral What is the measure of ∠AEB? 2 What is the measure of each interior angle of a 1) 36º regular hexagon? 2) 54º 1) 60° 3) 72º 2) 120° 4) 108º 3) 135° 4) 270° 6 What is the measure, in degrees, of each exterior angle of a regular hexagon? 3 Determine, in degrees, the measure of each interior 1) 45 angle of a regular octagon. 2) 60 3) 120 4) 135 4 Determine and state the measure, in degrees, of an interior angle of a regular decagon. 7 A stop sign in the shape of a regular octagon is resting on a brick wall, as shown in the accompanying diagram. What is the measure of angle x? 1) 45° 2) 60° 3) 120° 4) 135° 1 Regents Exam Questions Name: ________________________ G.CO.C.11: Interior and Exterior Angles of Polygons 2a www.jmap.org 8 One piece of the birdhouse that Natalie is building 12 The measure of an interior angle of a regular is shaped like a regular pentagon, as shown in the polygon is 120°. How many sides does the polygon accompanying diagram. have? 1) 5 2) 6 3) 3 4) 4 13 Melissa is walking around the outside of a building that is in the shape of a regular polygon.
[Show full text]
The First Treatments of Regular Star Polygons Seem to Date Back to The
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Archivio istituzionale della ricerca - Università di Palermo FROM THE FOURTEENTH CENTURY TO CABRÌ: CONVOLUTED CONSTRUCTIONS OF STAR POLYGONS INTRODUCTION The first treatments of regular star polygons seem to date back to the fourteenth century, but a comprehensive theory on the subject was presented only in the nineteenth century by the mathematician Louis Poinsot. After showing how star polygons are closely linked to the concept of prime numbers, I introduce here some constructions, easily reproducible with geometry software that allow us to investigate and see some nice and hidden property obtained by the scholars of the fourteenth century onwards. Regular star polygons and prime numbers Divide a circumference into n equal parts through n points; if we connect all the points in succession, through chords, we get what we recognize as a regular convex polygon. If we choose to connect the points, starting from any one of them in regular steps, two by two, or three by three or, generally, h by h, we get what is called a regular star polygon. It is evident that we are able to create regular star polygons only for certain values of h. Let us divide the circumference, for example, into 15 parts and let's start by connecting the points two by two. In order to close the figure, we return to the starting point after two full turns on the circumference. The polygon that is formed is like the one in Figure 1: a polygon of “order” 15 and “species” two.
[Show full text]
Formulas Involving Polygons - Lesson 7-3
you are here > Class Notes – Chapter 7 – Lesson 7-3 Formulas Involving Polygons - Lesson 7-3 Here’s today’s warmup…don’t forget to “phone home!” B Given: BD bisects ∠PBQ PD ⊥ PB QD ⊥ QB M Prove: BD is ⊥ bis. of PQ P Q D Statements Reasons Honors Geometry Notes Today, we started by learning how polygons are classified by their number of sides...you should already know a lot of these - just make sure to memorize the ones you don't know!! Sides Name 3 Triangle 4 Quadrilateral 5 Pentagon 6 Hexagon 7 Heptagon 8 Octagon 9 Nonagon 10 Decagon 11 Undecagon 12 Dodecagon 13 Tridecagon 14 Tetradecagon 15 Pentadecagon 16 Hexadecagon 17 Heptadecagon 18 Octadecagon 19 Enneadecagon 20 Icosagon n n-gon Baroody Page 2 of 6 Honors Geometry Notes Next, let’s look at the diagonals of polygons with different numbers of sides. By drawing as many diagonals as we could from one diagonal, you should be able to see a pattern...we can make n-2 triangles in a n-sided polygon. Given this information and the fact that the sum of the interior angles of a polygon is 180°, we can come up with a theorem that helps us to figure out the sum of the measures of the interior angles of any n-sided polygon! Baroody Page 3 of 6 Honors Geometry Notes Next, let’s look at exterior angles in a polygon. First, consider the exterior angles of a pentagon as shown below: Note that the sum of the exterior angles is 360°.
[Show full text]
Teacher Notes
TImath.com Algebra 2 Determining Area Time required 45 minutes ID: 8747 Activity Overview This activity begins by presenting a formula for the area of a triangle drawn in the Cartesian plane, given the coordinates of its vertices. Given a set of vertices, students construct and calculate the area of several triangles and check their answers using the Area tool in Cabri Jr. Then they use the common topological technique of dividing a shape into triangles to find the area of a polygon with more sides. They are challenged to develop a similar formula to find the area of a quadrilateral. Topic: Matrices • Calculate the determinant of a matrix. • Applying a formula for the area of a triangle given the coordinates of the vertices. • Dividing polygons with more than three sides into triangles to find their area. • Developing a similar formula for the area of a convex quadrilateral. Teacher Preparation and Notes • This activity is designed to be used in an Algebra 2 classroom. • Prior to beginning this activity, students should have an introduction to the determinant of a matrix and some practice calculating the determinant. • Information for an optional extension is provided at the end of this activity. Should you not wish students to complete the extension, you may have students disregard that portion of the student worksheet. • To download the student worksheet and Cabri Jr. files, go to education.ti.com/exchange and enter “8747” in the quick search box. Associated Materials • Alg2Week03_DeterminingArea_worksheet_TI84.doc • TRIANGLE (Cabri Jr. file) • HEPTAGON (Cabri Jr. file) Suggested Related Activities To download any activity listed, go to education.ti.com/exchange and enter the number in the quick search box.
[Show full text]
Polygrams and Polygons
Poligrams and Polygons THE TRIANGLE The Triangle is the only Lineal Figure into which all surfaces can be reduced, for every Polygon can be divided into Triangles by drawing lines from its angles to its centre. Thus the Triangle is the first and simplest of all Lineal Figures. We refer to the Triad operating in all things, to the 3 Supernal Sephiroth, and to Binah the 3rd Sephirah. Among the Planets it is especially referred to Saturn; and among the Elements to Fire. As the colour of Saturn is black and the Triangle that of Fire, the Black Triangle will represent Saturn, and the Red Fire. The 3 Angles also symbolize the 3 Alchemical Principles of Nature, Mercury, Sulphur, and Salt. As there are 3600 in every great circle, the number of degrees cut off between its angles when inscribed within a Circle will be 120°, the number forming the astrological Trine inscribing the Trine within a circle, that is, reflected from every second point. THE SQUARE The Square is an important lineal figure which naturally represents stability and equilibrium. It includes the idea of surface and superficial measurement. It refers to the Quaternary in all things and to the Tetrad of the Letter of the Holy Name Tetragrammaton operating through the four Elements of Fire, Water, Air, and Earth. It is allotted to Chesed, the 4th Sephirah, and among the Planets it is referred to Jupiter. As representing the 4 Elements it represents their ultimation with the material form. The 4 angles also include the ideas of the 2 extremities of the Horizon, and the 2 extremities of the Median, which latter are usually called the Zenith and the Nadir: also the 4 Cardinal Points.
[Show full text]