Model Performances Evaluated for Infinite Dilution Activity Coefficients
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Aqueous Hydrocarbon Systems: Experimental Measurements and Quantitative Structure-Property Relationship Modeling
AQUEOUS HYDROCARBON SYSTEMS: EXPERIMENTAL MEASUREMENTS AND QUANTITATIVE STRUCTURE-PROPERTY RELATIONSHIP MODELING By BRIAN J. NEELY Associate of Science Ricks College Rexburg, Idaho 1985 Bachelor of Science Brigham Young University Provo, Utah 1990 Master of Science Oklahoma State University Stillwater, Oklahoma 1996 Submitted to the Faculty of the Graduate College of the Oklahoma State University in partial fulfillment of the requirements for the Degree of DOCTOR OF PHILOSOPHY May, 2007 AQUEOUS HYDROCARBON SYSTEMS: EXPERIMENTAL MEASUREMENTS AND QUANTITATIVE STRUCTURE-PROPERTY RELATIONSHIP MODELING Dissertation Approved: K. A. M. Gasem DISSERTATION ADVISOR R. L. Robinson, Jr. K. A. High M. T. Hagan A. Gordon Emslie Dean of the Graduate College ii Preface The objectives of the experimental portion of this work were to (a) evaluate and correlate existing mutual hydrocarbon-water LLE data and (b) develop an apparatus, including appropriate operating procedures and sampling and analytical techniques, capable of accurate mutual solubility (LLE) measurements at ambient and elevated temperatures of selected systems. The hydrocarbon-water systems to be studied include benzene-water, toluene-water, and 3-methylpentane-water. The objectives of the modeling portion of this work were to (a) develop a quantitative structure-property relationship (QSPR) for prediction of infinite-dilution activity coefficient values of hydrocarbon-water systems, (b) evaluate the efficacy of QSPR models using multiple linear regression analyses and back propagation neural networks, (c) develop a theory based QSPR model, and (d) evaluate the ability of the model to predict aqueous and hydrocarbon solubilities at multiple temperatures. I wish to thank Dr. K. A. M. Gasem for his support, guidance, and enthusiasm during the course of this work and Dr. -

Separation of Acetic Acid/4-Methyl-2-Pentanone, Formic
Separation of acetic acid/4-methyl-2-pentanone, formic acid/4-methyl-2-pentanone and vinyl acetate/ethyl acetate by extractive distillation by Marc Wayne Paffhausen A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Chemical Engineering Montana State University © Copyright by Marc Wayne Paffhausen (1989) Abstract: Extractive distillation of the acetic acid/4-methyl-2-pentanone, formic acid/4-methyl-2-pentanone and vinyl acetate/ethyl acetate close boiling systems was investigated. Initial screening of potential extractive agents was carried out for each system in an Othmer vapor-liquid equilibrium still. Well over one hundred extractive agents, either alone or in combination with other compounds, were investigated overall. Subsequent testing of selected agents was carried out in a perforated-plate column which has been calibrated to have the equivalent of 5.3 theoretical plates. Relative volatilities for extractive distillation trial runs made in the perforated-plate column were calculated using the Fenske equation. All three systems investigated were successfully separated using chosen extractive agents. The use of polarity diagrams as an additional initial screening device was found to be a simple and effective technique for determining potential extractive agents as well. Decomposition of acetic acid during one of the test runs in the perforated-plate column was believed to have led to the discovery of ketene gas, which is both difficult to obtain and uniquely useful industrially. SEPARATION -

Prediction of Finite Concentration Behavior from Infinite
Iraqi Journal of Chemical and Petroleum Engineering Vol.11 No.3 (September 2010) 33 - 46 University of Baghdad ISSN: 12010-4884 College of Engineering Iraqi Journal of Chemical and Petroleum Engineering PREDICTION OF FINITE CONCENTRATIONBEHAVIOR FROM INFINITE DILUTION EGUILIBRIUM DATA Prof Dr. Mahmoud O. Abdullahil; Dr. Venus M Hameed*; Basma M. Haddad Chemical Engineering Department – University of Nahrin ___________________________________________________________________________________ ABSTRACT Experimental activity coefficients at infinite dilution are particularly useful for calculating the parameters needed in an expression for the excess Gibbs energy. If reliable values of γ∞1 and γ∞2 are available, either from direct experiment or from a correlation, it is possible to predict the composition of the azeotrope and vapor-liquid equilibrium over the entire range of composition. These can be used to evaluate two adjustable constants in any desired expression for G E. In this study MOSCED model and SPACE model are two different methods were used to calculate γ∞1 and γ∞2 _______________________________________________________________________________________________ INTRODUCTION Activity coefficients at infinite dilution have equations have three parameters. For NRTL many uses, some of them: calculating the equation parameters are τ12, τ21 and α22 where Vapor Liquid Equilibrium for any mixture, α12 is related to the non randomness in the finding the azeotrope composition and pressure; mixture, the others are considered as energy and the estimation of mutual solubility. These parameters. The UNIQUAC equation contains calculations are carried out by finding the two three parameters, u12 and u21 adjustable binary adjustable parameters of any desired expression energy parameters and the third parameter is for GE (Wilson [1], NRTL [2] and UNTQUAC considered as coordination number designated [3] equations. -

Iispip THIS IS to C&Jttijrv THAT the THESIS
iispip THIS IS TO C&jttijrv THAT THE THESIS PREPARED UNDER M ¥ SUPERVISION BY ••MSlIMtMMMfMOMtlMBIM****••••••»•****♦**• »•«*>»«« to* ........ .......( * E A © OP D M A R H K N T OP.-- £bSgil9.al_£.Qg.ineering Modification of the MOSCED Equation to Xaprove Prod let ions of Vapor-I>lquid Equilibria . By Kevin M. Stephenson Thesis for the Degree of Bachelor of Science in Chemical Engineering Col lege of Liberal Arts and Sciences University of Illinois Urbana, Illinois 1988 Table of Contents Summary....................... j_2 Introduction.................. 3-4 Objective..................... 5 Strategy...................... 6 Procedure.................. t # Results.................... q Conclusions................t ^ Acknowledgements............. n References.................... 12-16 Appendix ...... ............. A 3—A 130 Ifamenelature........... m B C W parameters--- ,. A3-A5 Ramlet-Taft parameters A6-A 19 Identification list.... A20-A33 Alkane ID list......... ^34 r„ llst.......... A35-A105 T analysis.............A106-A109 Fitting Program........ A U 0 - A 1 S 0 Fitting Subroutines....A123-A124 Program Output......... A125-A130 Th« project undertaken as a Chemical Engineering 292/390 assignment was to reparameterize the MOSCED equation. This equation predicts activity coefficients at infinite dilution which can he used to predict VI,E behavior. Typically VLE behavior is predicted from the differences in two compounds of the energy required to remove a molecule from its environment due to physical and chemical interactions {its cohesive energy density). The MOSCED equation extends the applicability of such equations to polar and associating systems by assuming the cohesive energy density can be separated into independent, additive components. The goal of this project was to redefine the equations relating these components to physically measurable quantities and to see if this change would improve the predictive ability of the equation. -

A Study of the Reversing of Relative Volatilities by Extractive Distillation
A study of the reversing of relative volatilities by extractive distillation by An-I Yeh A thesis submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Chemical Engineering Montana State University © Copyright by An-I Yeh (1986) Abstract: The separation of the close-boiling mixture, m-xylene-o-xylene; three binary azeotropes: ethanol-water, methyl acetate-methanol, acetone-methanol, and four ternary azeotropes: n-propyl acetate-n-propanol-water, isopropyl acetate-isopropanol-water, n—butyl acetate-n- butanol-water, isobutyl acetate-isobutanol-water has been enhanced by extractive distillation. The azeotropes have been negated and the relative volatilities of key components have been reversed by the agents used. The plot of polar interaction versus hydrogen bonding, called polarity diagram, was used to compare the affinity of agents for key components. Thus the key component which will be the overhead product can be predicted. The three solubility parameters were used to describe the intermolecular forces occurring between agents and key components in extractive distillation. The MOSCED model was used to calculate the activity coefficients of the key components using the properties of the pure compounds. The calculated values fitted the experimental data well. The advantage of this model was to calculate the. relative volatilities of key components in the presence of the agent using the properties of pure compounds instead of using the properties of mixtures. Temperature inversion, where the overhead temperature was higher than the stillpot temperature, was observed for the acetone-methanol system when ketones were used as the agents. The data showed that the temperature inversion could be caused by the dissolving of the vapor of key components in the liquid agents. -

New Tools for Teaching Chemical Engineering Thermodynamics J
Equation Section 1 New Tools for Teaching Chemical Engineering Thermodynamics J. Richard Elliott Chemical and Biomolecular Engineering Dept. The University of Akron Akron, OH 44325-3906 [email protected] Abstract. The teaching toolbox described by Elliott and Lira (2000) has been expanded to include three new tools: molecular simulation, ConcepTesting, and a simplified version of the MOSCED model. The previous list of tools included: detailed derivations (e.g. Maxwell's relations), computational tools (calculator and xls), projects, homework, analogies, examples, tours, tests (including samples from past years), quizzes, and help sessions. Students were surveyed to rank these tools from “most instructive” to “least.” The new tools are described briefly and the survey assessments are presented. The molecular simulation tool focuses on applets posted at: http://rheneas.eng.buffalo.edu/wiki/DMD. These applets provide visualization of molecular dynamics for ideal gases, hard spheres, and square-well spheres. The students are guided through several homework assignments in which they learn about temperature, energy, pressure, and system size. Further details are available online, so the remainder of this abstract focuses on the Simplified Separation of Cohesive Energy Density (SSCED). In the current work, the acidity and basicity parameters are adopted directly from the latest literature, but the polarity and dispersion parameters are lumped together and the total of all contributions is constrained to match the original Scatchard-Hildebrand solubility parameter. Three composition-dependent parameters of the MOSCED model are set to constants. In this way, the contrast between the physical interactions and the chemical interactions is more readily apparent and the model can be applied directly at all compositions in a self-consistent manner. -

Solvent Screening Using Unifac Method to Investigate the Deodorization of Soybean Oil Using a Liquid Solvent
SOLVENT SCREENING USING UNIFAC METHOD TO INVESTIGATE THE DEODORIZATION OF SOYBEAN OIL USING A LIQUID SOLVENT P. O. B. HOMRICH, R. CERIANI Universidade Estadual de Campinas, Faculdade de Engenharia Química, Departamento de Desenvolvimento de Processos e Produtos E-mail para contato: [email protected] ABSTRACT – Removal of secondary oxidation products from edible oils, currently achieved by steam stripping in the deodorization process, may be conducted under mild conditions with a liquid solvent. Solvent screening can be used to determine more suitable solvents for removing undesirable compounds. In order to investigate the removal of n- hexanal, 2,4-decadienal and hexanoic acid, odor compounds of soybean oil, 16 solvents with low toxicity were preselected by using the qualitative method of Cusack et al. (1991). Solubility data of pseudoternary (diluent + solute + solvent) and binary (solvent + solvent) systems were predicted using UNIFAC at 298.15 K and under 1 atm in Aspen Plus. Two versions of UNIFAC were considered, namely, Magnussen et al. (1981) and Hirata et al. (2013). This last version is specifically adjusted for lipid technology systems. In general, the results indicated that 7 solvents presented a separation region (type I or II), with different mutual solubility for the solvent/diluent pair. In addition, a partial miscibility were verified for three binary systems of solvents and water. This simulated screening was a guidance for sets of experiments involving liquid-liquid equilibria under investigation currently in our lab. 1. INTRODUCTION The deodorization of vegetable oils causes various deleterious consequences, such as the removal of nutraceutical compounds, the degradation of triacylglycerol, the undesirable reactions of oxidation and cis-trans isomerization, and the 3-MCPD (3-monochloropropane-1,2-diol) contaminant formation (Suliman and Jiang, 2013; Szydłowska-Czerniak et al., 2011; Ermacora and Hrncirik, 2014). -

Searching for an Experimental Procedure for the Measurement of Alkane-Water Partition Coefficient
Searching for an Experimental Procedure for the Measurement of Alkane-Water Partition Coefficient Hind Gharbi Dissertation presented to Escola Superior de Tecnologia e Gestão Instituto Politécnico de Bragança In order to obtain Master’s Degree in Chemical Engineering This work was supervised by Maria Olga Amorim e Sá Ferreira Simão Pedro Almeida Pinho Radhia El Aissi July, 2019 Acknowledgements I would to thank my IPB supervisors for making this work possible. Professor Simao Pinho for being such a good guidance, for all the discussions pushing me to always look at things differently. Professor Maria Olga Amorim Ferreira for showing me how work must be done in her one kind gentle way. I would like to think all the research team for always being disposed to help and for the good vibes. Most important of all I dedicate this achievement to my mom and thank here for being my rock, for believing and supporting me, for the friendship, for the dictature, for the tenderness, love…for every(good :p) thing I am and everything I am not. For my dad, you’ll not see this but I miss you every day more, doing this work I thought of you during every step of the way. The brilliant and unique mind that you are is letting a huge hollow in this world...still feel your love and kindness. To the sweetest and craziest human being ever, I love these big beautiful eyes that always look at me as the most powerful super hero (will always be yours)! I thank God every day for giving me such a wonderful big little sister. -
UC Office of the President Recent Work
UC Office of the President Recent Work Title Infinite Dilution Activity Coefficients as Constraints for Force Field Parametrization and Method Development. Permalink https://escholarship.org/uc/item/3z62h3j0 Journal Journal of chemical theory and computation, 15(5) ISSN 1549-9618 Authors Duarte Ramos Matos, Guilherme Calabrò, Gaetano Mobley, David L Publication Date 2019-05-01 DOI 10.1021/acs.jctc.8b01029 License https://creativecommons.org/licenses/by/4.0/ 4.0 Peer reviewed eScholarship.org Powered by the California Digital Library University of California Infinite dilution activity coefficients as constraints for force field parameterization and method development , , Guilherme Duarte Ramos Matos,y Gaetano Calabr`o,z and David L. Mobley∗ { y Department of Chemistry, University of California, Irvine, CA y OpenEye Scientific Software, Santa Fe, NM z Department of Pharmaceutical Sciences, University of California, Irvine, CA { E-mail: [email protected] Abstract Molecular simulations begin with an underlying energy model or force field, and from this, can predict diverse physical properties. However, force fields were often developed with relatively limited datasets, yet accuracy for diverse properties across a broad chemical space is desirable, so tests of such accuracy are particularly impor- tant. Here, to this end, we calculate 237 infinite dilution activity coefficients (IDACs), comparing with experimental values from NIST's ThermoML database. We found that calculated IDAC values correlate strongly with experiment (Pearson R of 0:92 0:01), ± and allow us to identify specific functional groups which appear to present challenges to the force field employed. One potentially valuable aspect of IDACs, as compared to solvation free energies which have been frequently employed as force field tests, is that the same molecules serve both as solutes and solvents in different cases, allowing us to ensure force fields are not overly tuned to one particular environment or solvent. -

Solubility Science: Principles and Practice Prof Steven Abbott
Solubility Science: Principles and Practice Prof Steven Abbott Steven Abbott TCNF Ltd, Ipswich, UK and Visiting Professor, University of Leeds, UK [email protected] www.stevenabbott.co.uk Version history: First words written 15 Sep 2015 Version 1.0.0 15 Sep 2017 Version 1.0.1.1 05 Oct 2017 (Some additions on HSP) Version 1.0.1.2 05 Jan 2018 (An update on RDF calculations for large, complex solute molecules such as proteins) Version 1.0.1.3 05 April 2020 (A number of typos fixed thanks to the kind checking by Lee McManus) Version 1.0.2.0 March 2021 (Crystallization chapter added) Version 1.0.2.1 March 2021 (Minor crystallization updates) Version 1.0.2.1a March 2021 (Correction on NOESY) Copyright © 2017-21 Steven Abbott This book is distributed under the Creative Commons BY-ND, Attribution and No-Derivatives license. Contents Preface 6 Abbreviations and Symbols 10 1 Solubility Basics 12 1.1 The core concepts 15 1.1.1 Concentration 15 1.1.2 MVol 16 1.1.3 µ 17 1.1.4 G 17 1.1.5 a and γ 18 1.1.6 And a few other things 19 1.2 KB theory 19 1.2.1 Getting a feeling for Gij and Nij values 25 1.2.2 Measuring Gij values 27 1.2.3 Information from density 30 1.2.4 Pressure 31 1.2.5 A toy KB world 32 1.2.6 Excluded volume 33 1.2.7 Fluctuation theory 34 1.2.8 Scattering 36 1.2.9 What have we achieved with all this effort spent on KB? 36 1.3 Other solubility theories are available 37 1.3.1 Abraham parameters 37 1.3.2 MOSCED and PSP 38 1.3.3 UNIFAC 38 1.3.4 NRTL-SAC 39 1.3.5 The criteria for a successful solubility theory 39 2 Transforming solubility -
MKS 06160.Pdf
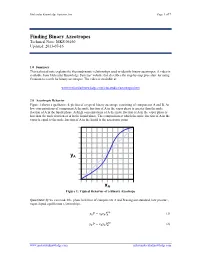
Molecular Knowledge Systems, Inc. Page 1 of 7 Finding Binary Azeotropes Technical Note: MKS 06160 Updated: 2013-07-16 1.0 Summary This technical note explains the thermodynamic relationships used to identify binary azeotropes. A video is available from Molecular Knowledge Systems’ website that describes the step-by-step procedure for using Cranium to search for binary azeotropes. The video is available at: www.molecularknowledge.com/casestudies/azeotropes.htm 2.0 Azeotropic Behavior Figure 1 shows a qualitative depiction of a typical binary azeotrope consisting of components A and B. At low concentrations of component A the mole fraction of A in the vapor phase is greater than the mole fraction of A in the liquid phase. At high concentrations of A the mole fraction of A in the vapor phase is less than the mole fraction of A in the liquid phase. The composition at which the mole fraction of A in the vapor is equal to the mole fraction of A in the liquid is the azeotropic point. yA xA Figure 1: Typical Behavior of a Binary Azeotrope Quantitatively we can model the phase behavior of components A and B using our standard, low pressure, vapor-liquid equilibrium relationships: = (1) 푣푝 푦퐴푃 푥퐴훾퐴푃퐴 = (2) 푣푝 푦퐵푃 푥퐵훾퐵푃퐵 www.molecularknowledge.com [email protected] Molecular Knowledge Systems, Inc. Page 2 of 7 The slope of the curve in Figure 1 is given by: = 푣푝 + 푣푝 (3) 휕푦퐴 훾퐴푃퐴 푥퐴푃퐴 휕훾퐴 휕푥퐴 푃 푃 휕푥퐴 As the concentration xA approaches 0 the slope approaches: = ∞ 푣푝 (4) 휕푦퐴 훾퐴 푃퐴 � 휕푥퐴 푥퐴=0 푃 Using the relationships: = 1 (5) 푦퐴 − 푦퐵 = 1 푣푝 (6) 푥퐵훾퐵푃퐵 푦퐴 − 푃 = 푣푝 푣푝 (7) 휕푦퐴 훾퐵푃퐵 휕푥퐵 푥퐵푃퐵 휕훾퐵 − − 휕푥퐴 푃 휕푥퐴 푃 휕푥퐴 + = 0 (8) 푑푥퐴 푑푥퐵 We obtain: = 푣푝 + 푣푝 (9) 휕푦퐴 훾퐵푃퐵 푥퐵푃퐵 휕훾퐵 휕푥퐴 푃 푃 휕푥퐵 As the concentration xA approaches 1 the slope approaches: = ∞ 푣푝 (10) 휕푦퐴 훾퐵 푃퐵 � 휕푥퐴 푥퐴=1 푃 Figure 1 shows that when an azeotrope is present the slopes at each concentration limit must both be either greater than 1 or less than 1. -

Abstract Efficient Early Stage Chemical Process
ABSTRACT EFFICIENT EARLY STAGE CHEMICAL PROCESS DESIGN by Pratik Dhakal Design of any chemical processes on a large scale such as distillation, extraction requires tremendous amount of data. Such data can be obtained either through literature review (if available), experiments, molecular, property prediction tools. Conducting experiments on a large scale for multicomponent mixtures at different variables can be quite expensive and time consuming, while molecular simulation is still computationally demanding even though it can provide accurate molecular level details. Property prediction tools are simple analytical model based on empirical relations or thermodynamics relations that can provide accurate estimates, which is why they are used throughout the industry. However, most commons property predictions tools provide no qualitative insight on a molecular level that could be extremely useful for process intensifications. Thus, this research is focused on a analytical model called MOSCED that has shown tremendous capability in providing accurate property predictions and qualitative molecular insights that could guide chemical process design during early stage. EFFICIENT EARLY STAGE CHEMICAL PROCESS DESIGN Thesis Submitted to the Faculty of Miami University in partial fulfillment of the requirements for the degree of Master of Science by Pratik Dhakal Miami University Oxford, Ohio 2018 Advisor: Dr.Andrew Paluch Reader: Catherine Almquist Reader: Dr Shashi Lalvani ©2018 Pratik Dhakal This thesis titled EFFICIENT EARLY STAGE CHEMICAL PROCESS