DOCSLIB.ORG

The Mathematics Values in Classroom Inventory: Development and Initial

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Mathematics Values in Classroom Inventory: Development and Initial Malaysian Online Journal of Educational Sciences 2017 (Volume5 - Issue 2 ) The Mathematics Values In Classroom [1] INTEC Education College, Inventory: Development And Initial Shah Alam, Selangor, Malaysia [2] Faculty of Education, University Validation of Malaya Ruzela Tapsir [1], Nik Azis Nik Pa [2] ABSTRACT Value has been identified as an essential aspect towards the quality in mathematics education at various levels of the system, institutional, curriculum, education management, and classroom interactions. However, few studies were focused on values, its development, measurement, and impact in education as compared to other affective aspects such as beliefs, motivation, perceptions, and attitude. In addition, most studies dealt with values developed in Western education setting where the spiritual domain was not considered. This paper detailed the instrument development processes including analysis, design, development, and evaluation phases. Content validity of the 36-item instrument was enhanced by a focus group and panels of experts’ reviews. Construct validity was investigated using reliability measures, item analysis, principal analysis of residuals, rating scale functioning, confirmatory factor analysis, and first order factor analysis. The inventory, three sub-constructs, nine dimensions, and the 36 items have high Cronbach alpha values. Confirmatory factor analysis did not fully support the hypothesised conceptual framework with three sub-constructs and nine dimensions. Suggestions on how to further improve the instrument validity were proposed. The instrument which was theoretically based on faith and belief in God, was the pioneer and significant to the future investigations on values development in mathematics education. Keywords: Instrument development; universal integrated approach; values development, validity. INTRODUCTION Integrating values in the teaching and learning mathematics has not been an easy task for teachers, since it would require for the teachers to know important values to be integrated and how to develop them in classrooms. Currently, the quality of values development and ethics in mathematics education in Malaysia remained at low level and the activities conducted were not exhaustive and not integrated. We were still far from fulfilling the pinnacle of values development which is to produce civilized individuals who would act and behave appropriately according to specific guidelines and able to make righteous decisions in critical situations (Nik Azis, 2014). Literature Review Literature showed that there was little agreement on the conceptions of values as well as its categorization. Conceptualizations of values were normally based on the context of usage, suggesting that a single definition may not suit the many arising situations concerning values. Adding to the complication was the situation where conceptions and constructs were sometimes borrowed from other fields like psychology and sociology while ignoring the basic assumptions of the constructs. Among the popular definitions were: 82 www.moj-es.net Malaysian Online Journal of Educational Sciences 2017 (Volume5 - Issue 2 ) values as ideal culture with the focus on evaluation Rokeach (1973), values from the context of relativism epistemology where man was the authority in evaluating and determining values (Raths, Harmin & Simon, 1966), and values as sociological factors especially on principles and standards used to guide human behaviour (Halsted & Taylor, 2000). Values in mathematics classrooms were often attributed to the earlier socio-cultural definitions constructed by Bishop (1988) where values were considered as deep affective values. The conceptions were mainly developed in the context of the western education culture unlike the definitions proposed by Nik Azis (2009) which took into consideration the metaphysical aspect. There were limited studies in the area of values in mathematics education and its development since value was relatively a new area of research interest as compared to other affective constructs such as beliefs, attitude, motivation, and perceptions (Seah & Bishop, 2000). In addition, teaching mathematics was usually aimed at acquisition of knowledge while providing minimal emphasis on values in mathematics education (Bishop, 1988). Furthermore mathematics had been taught as a subject which was value free by teachers, employers and parents (Bishop, FitzSimons, Seah, 1999). There was also issue on availability of instruments measuring values in mathematics classrooms. Several prominent researchers had attempted to develop tools which could measure values in mathematics education and mathematics as a subject such as: Mathematics Values Instrument (Bishop, 1988), Mathematics Values Scale (Durmus & Bicak, 2006), and Mathematics Education Values Questionnaire (Dede, 2011). Bishop, Clarke, Corrigan and Gunstone (2005) designed an instrument to learn more on teachers’ preferences and practices regarding values in teaching mathematics and sciences. On the other hand, the Teachers’ Beliefs Survey (Beswick, 2005) touched on measure teachers’ consistency with a problem-solving view of mathematics and corresponding views of mathematics teaching and learning. The Mathematics Values Inventory (MVI) focused on mathematics values in terms of the achievement-related choices which focus on students’ beliefs in the area of interest, general utility, need for high achievement, and personal cost (Luttrell, Callen, Allen, Wood, Deeds, & Richard, 2010). Other instruments included instruments developed by Durmus and Bicak (2006) and Dede (2006 & 2009) from Turkey which categorized the values of mathematics and mathematics education into teachers and students centred values. Although instruments had been developed to measure values in mathematics classrooms, they were unsuitable for the Malaysian education purpose as they were designed based on psychological theories which were secular in nature. This was due to the fact that these instruments were developed in western culture which served the western needs where faith and belief in God were separated from daily activities. Furthermore, these instruments were mainly focusing on perceptual studies where the scope were limited in breadth and depth. Conceptual Framework of the Values in Mathematics Classrooms In the context of classroom settings, values in mathematics education were categorized into the universal values, mathematical education values and mathematics values where each one was further represented by several dimensions of values (Nik Azis, 2009). Bishop (1988) suggested that assessment of values was to detect the leading values between two complementary values leading towards balancing of the two complementary values for the sub-constructs. Nik Azis detailed out the work done by Bishop (1988) from the perspective of universal integrated approach by representing the dimensions of the sub-construct in a hierarchal manner. The universal integrated perspective which was based on believing in God referred values as conceptions and beliefs of individuals concerning the importance of something which act as general guides to their behaviours (Nik Azis, 2008, 2014). The conceptions of construct were based on the basic definitions on values and ethics development according to the teaching of Islam which were systematically structured by Syed Muhammad Naquib (1995). The conception follows definition provided by Al-Ghazali (1990) where value was conceptualized as an intellectual discipline, known as adab. It was referred as the appreciation and acknowledgement of the reality that knowledge and human hierarchically were ordered according to certain grades and degree of rank, and of one’s proper place in relation to reality and to one’s physical, intellectual, and spiritual capacities and potentials. 83 www.moj-es.net Malaysian Online Journal of Educational Sciences 2017 (Volume5 - Issue 2 ) In terms of the sub-constructs, values in mathematics classrooms were categorized into universal values, mathematical values, and mathematics values. Universal values which were values contributed towards the formation of a good human with good characteristics while mathematics education values were values related to effective learning and teaching. Mathematics values on the other hand were related to the sources, limitations, and reliability, on the truth of mathematics as one of the discipline in knowledge within a particular culture. Bishop’s work did not include conceptual definition for the universal values. The universal values proposed by Bishop was associated with the norms of an educational institution within a particular society which had a particular culture. Nik Azis (2016) expanded the definition of universal values following the Hierarchy Categories of Values Model in which faith was proposed to be the fundamental values (values as guidance in life), followed by the core (values as necessity in life), main (values portraying oneself) and development (self-development values). The mathematics education values were divided into the values in teaching and learning. Teaching was categorized into teach for higher mathematics, teach for functionality, teach to generate knowledge, and teach to internalize knowledge. Values for learning included learning for mastering skills, learning for processing information, learning for construction of knowledge, and learning for obtaining knowledge. The mathematics values were being categorized as ideological, sentimental, and sociological aspects.
Load more

Recommended publications
  • Mengenai FWD Takaful Berhad
    Program Biasiswa 1 Program Biasiswa FWD Takaful Mengenai FWD Takaful Berhad FWD Takaful Berhad (“FWD Takaful”) adalah pengendali Takaful di Malaysia yang menawarkan perkhidmatan Takaful keluarga. FWD Takaful dilesenkan di bawah Akta Perkhidmatan Kewangan Islam 2013 dan dikawal selia oleh Bank Negara Malaysia. Ia adalah unit perniagaan Takaful Kumpulan FWD (“FWD”) - yang merentasi Hong Kong & Macau, Thailand, Indonesia, Filipina, Singapura, Vietnam, Jepun dan Malaysia; menawarkan insurans hayat dan perubatan, insurans am, pelan perlindungan pekerja, pelan perlindungan Shariah dan Takaful keluarga merentasi beberapa pasarannya. FWD menumpukan usaha untuk mencipta pengalaman pelanggan yang baru dan menjadikan insurans lebih mudah, cepat dan lancar, dengan pembaharuan yang inovatif dan pelan perlindungan yang mudah difahami, disokong oleh teknologi digital. Melalui pendekatan yang didorong oleh pelanggan ini, FWD mensasarkan untuk menjadi peneraju insurans Asian yang mengubah pandangan terhadap insurans. Ditubuhkan di Asia pada tahun 2013 dengan matlamat sebagai perintis, FWD adalah perniagaan insurans utama kumpulan pelaburan, Pacific Century Group. Untuk maklumat lanjut, sila layari fwd.com.my. 1 Program Biasiswa FWD Takaful Program Biasiswa FWD Takaful FWD Takaful menawarkan program biasiswa kepada pelajar-pelajar Malaysia daripada keluarga berpendapatan kurang daripada RM5000 atau dalam golongan B40 yang memerlukan bantuan kewangan untuk meneruskan pelajaran ke institusi pengajian tinggi. Program biasiswa ini akan membiayai sepenuhnya pengajian untuk tempoh 4 tahun (termasuk pra-universiti bagi pelajar lepasan SPM ) di universiti yang tersenarai. Tujuan biasiswa ini bertujuan untuk membolehkan pelajar yang cemerlang dalam pengajian mereka mendapatkan kemahiran dan pengetahuan yang lebih mendalam. Kami menggalakkan dan mendorong pelajar-pelajar ini untuk melanjutkan pengajian dalam bidang Takaful/Insurans, Syariah, Kewangan/ Kewangan Islam, Teknologi Maklumat dan Sains Aktuari.
    [Show full text]
  • 7Th MELTA International Research Conference in English Language Education 2017
    7th MELTA International Research Conference in English Language Education 2017 TESL BLOCK Institut Pendidikan Kampus Ilmu Khas, Kuala Lumpur, Malaysia Saturday, 25 November 2017 In Collaboration with Institut Pendidikan Kampus Ilmu Khas Acknowledgement MELTA gratefully acknowledges the following for their support and contribution for the 7th MELTA International Research Conference in English Language Education 2017 • YBhg. Dato’ Sulaiman bin Wak, Timbalan Ketua Pengarah Pelajaran Malaysia (Dasar dan Pembangunan Pendidikan), Kementerian Pendidikan Malaysia • YBrs. Dr. Sariah binti Abdul Jalil, Rector, Institute Pendidikan Guru Malaysia • Director, IPG Kampus Ilmu Khas • Director, Institut Latihan DBKL • Director, IPG Kampus Bahasa Antarabangsa • Head of Department, English Studies Department, IPG Kampus Ilmu Khas • All participants, institutions and volunteers for their participation. ___________________________________________ ©2017 Malaysian English Language Teaching Association G-11-2, Putra Walk Jalan PP25, Taman Pinggiran Putra, Bandar Putra Permai, 43300 Seri Kembangan, Selangor All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, 2 Disclaimerwithout the prior permission of the copyright owner. Neither the publisher nor the editors accept responsibility for the views of authors expressed in their contributions. Contents 4 Message by Timbalan Ketua Pengarah Pelajaran Malaysia, Kementerian
    [Show full text]
  • Burnout, Personality, and Social Support: a Case of Malaysian Academics
    International Conference on Trade, Tourism and Management (ICTTM'2012) December 21-22, 2012 Bangkok (Thailand) Burnout, Personality, and Social Support: A Case of Malaysian Academics Fauziah Noordin1, Rohana Othman2, Ismie Roha Mohd Jais3, Janudin Sardi4 Abstract— The objectives of this study is to assess the level of II. BURNOUT, PERSONALITY, AND SOCIAL SUPPORT burnout among the academic staff; to examine the correlations of Maslach and Jackson [5] defined burnout as a syndrome personality and social support to the three components of burnout that is composed of three dimensions: emotional exhaustion, of the academic staff; and to determine the influence of selected demographic variables on the three components of burnout, depersonalisation, and reduced personal accomplishment. personality, and social support of the academics. The results show Emotional exhaustion refers to demands and stressors that that depersonalization and negative temperament indicate low mean cause people to feel overwhelmed and unable to give of scores; emotional exhaustion, positive temperament, and social themselves at a psychological level. Depersonalization is the support (friends), moderate mean scores; and personal development of negative and cynical attitudes that can create accomplishment, social support (significant other), and social a callous view of others, perceiving them as deserving of support (family) show high mean scores. The results of correlation their troubles. Reduced sense of personal accomplishment is analyses indicated several significant correlations between the the tendency to view oneself negatively and to be dissatisfied studied variables. The results of the independent group t-tests and with accomplishments. one-way between group ANOVA with post-hoc comparison indicate significant findings between the studied variables and Findings of previous research reported that burnout is selected demographic variables.
    [Show full text]
  • Senarai Singkatan Perpustakaan Di Malaysia
    F EDISI KETIGA SENARAI SINGKATAN PERPUSTAKAAN DI MALAYSIA Edisi Ketiga Perpustakaan Negara Malaysia Kuala Lumpur 2018 SENARAI SINGKATAN PERPUSTAKAAN DI MALAYSIA Edisi Ketiga Perpustakaan Negara Malaysia Kuala Lumpur 2018 © Perpustakaan Negara Malaysia 2018 Hak cipta terpelihara. Tiada bahagian terbitan ini boleh diterbitkan semula atau ditukar dalam apa jua bentuk dengan apa cara jua sama ada elektronik, mekanikal, fotokopi, rakaman dan sebagainya sebelum mendapat kebenaran bertulis daripada Ketua Pengarah Perpustakaan Negara Malaysia. Diterbitkan oleh: Perpustakaan Negara Malaysia 232, Jalan Tun Razak 50572 Kuala Lumpur 03-2687 1700 03-2694 2490 03-2687 1700 03-2694 2490 www.pnm.gov.my www.facebook.com/PerpustakaanNegaraMalaysia blogpnm.pnm.gov.my twitter.com/PNM_sosial Perpustakaan Negara Malaysia Data Pengkatalogan-dalam-Penerbitan SENARAI SINGKATAN PERPUSTAKAAN DI MALAYSIA – Edisi Ketiga eISBN 978-983-931-275-1 1. Libraries-- Abbreviations --Malaysia. 2. Libraries-- Directories --Malaysia. 3. Government publications--Malaysia. I. Perpustakaan Negara Malaysia. Jawatankuasa Kecil Senarai Singkatan Perpustakaan di Malaysia. 027.002559 KANDUNGAN Sekapur Sirih .................................................................................................................. i Penghargaan .................................................................................................................. ii Prakata ........................................................................................................................... iii
    [Show full text]
  • (Jpa) Bagi Mengikuti Pengajian Peringkat Persediaan Dan Ijazah Pertama Di Bawah Program Khas Jepun, Korea, Perancis Dan Jerman (Jkpj) Tahun 2020
    TAWARAN PENAJAAN JABATAN PERKHIDMATAN AWAM (JPA) BAGI MENGIKUTI PENGAJIAN PERINGKAT PERSEDIAAN DAN IJAZAH PERTAMA DI BAWAH PROGRAM KHAS JEPUN, KOREA, PERANCIS DAN JERMAN (JKPJ) TAHUN 2020 PENGENALAN Permohonan adalah dipelawa kepada calon-calon yang menduduki Sijil Pelajaran Malaysia (SPM) pada tahun 2019 bagi kali pertama untuk mendapatkan penajaan Jabatan Perkhidmatan Awam (JPA) dalam bentuk Pinjaman Boleh Ubah (PBU) di bawah Program Khas Jepun, Korea, Perancis, dan Jerman (JKPJ). Mulai tahun 2020, Kerajaan telah menambah baik program ini dengan memberikan peluang kepada pelajar untuk menyambung pengajian ke negara China. Program penajaan ini dibuka kepada semua pelajar lepasan SPM tahun 2019 yang berminat dalam bidang kejuruteraan, sains dan teknologi (S&T) dan sains sosial di negara Jepun, Korea, Perancis, Jerman dan China. Pelajar akan ditaja untuk mengikuti program persediaan sebelum melanjutkan pengajian ke peringkat diploma atau ijazah pertama di negara-negara berkenaan. 1. STRUKTUR PENGAJIAN PROGRAM KHAS JKPJ Struktur pengajian bagi Program Khas JKPJ adalah seperti berikut: PERSEDIAAN PROGRAM / IJAZAH TEMPAT KOLEJ KURSUS TEMPOH Kejuruteraan INTEC Persediaan Dip. : 3 tahun Teknikal Education Teknikal 24 bulan I.P. : 2 tahun Jepun College Jepun 1) INTEC CGPA 3.75 Ke Education Atas – College Persediaan 1) 9 bulan I.P. : 4 tahun Khas Korea dan 2) Pusat Sijil Bahasa 2) 12 bulan CGPA 3.74 Ke Pengajian Bawah – Bahasa di Dip. : 2 tahun Korea I.P. : 2 tahun 1 bulan INTEC + Diplome Education Persediaan d’Ingenieur : College di Perancis 5 tahun Khas (12 bulan) Persediaan Perancis 13 bulan Malaysia + DUT : 2 tahun France 2 bulan I.P. : 3 tahun Institute (MFI) (Bridging Program) INTEC Bch.
    [Show full text]
  • Ytp) Lepasan Spm 2020
    PROGRAM PEMBANGUNAN BAKAT MUDA YOUNG TALENT DEVELOPMENT PROGRAMME (YTP) LEPASAN SPM 2020 BIL. PROGRAM KOD PROGRAM SYARAT KELAYAKAN MAKLUMAT PENGAJIAN LALUAN LUAR NEGARA 1. KOLEJ MARA BANTING (KMB) Mendapat sekurang-kurangnya Gred A- Pelajar akan mengikuti Program International Baccalaureate (IB) dalam LAPAN (8) subjek berikut: selama dua (2) tahun di Kolej MARA Banting (KMB) dan pelajar berpeluang menyambung pengajian ke peringkat Ijazah Sarjana Muda 1) Bahasa Melayu; di universiti terpilih dalam bidang / kursus pengajian seperti berikut: 2) Bahasa Inggeris; IB SAINS HAYAT MARA0101_2021 3) Matematik; 1) Pharmacy 4) Matematik Tambahan; 5) Biologi; 6) Fizik; 7) Kimia; 8) Satu (1) subjek lain Mendapat sekurang-kurangnya Gred A- Pelajar akan mengikuti Program International Baccalaureate (IB) dalam TUJUH (7) subjek berikut: selama dua (2) tahun di Kolej MARA Banting (KMB) dan pelajar berpeluang menyambung pengajian ke peringkat Ijazah Sarjana Muda 1) Bahasa Inggeris; di universiti terpilih dalam bidang / kursus pengajian seperti berikut : 2) Matematik Tambahan; 3) Biologi/ Sains Komputer/ Lukisan a) Bidang Sains Kesihatan & Sains Tulen: Kejuruteraan/ Kej. Awam/ Kej. Elektrik/ Kej. 1) Biomedical Science 9) Audiology/ Speech Pathology Mekanikal/ Reka Cipta; 2) Biochemistry 10) Medical Imaging/ Radiology 4) Fizik; 3) Biotechnology 11) Geology/ Geophysics/Geoscience IB SAINS 5) Kimia; 4) Biological Science 12) Sports Medicine Rehabilitation (SAINS KESIHATAN & MARA0102_2021 6) Dua (2) subjek lain 5) Physiology 13) Veterinary Science SAINS KOMPUTER)
    [Show full text]
  • PS Halal Studies
    i Programme Standards: Halal Studies First Edition 2020 Malaysian Qualifications Agency Mercu MQA No. 3539, Jalan Teknokrat 7 Cyber 5 63000 Cyberjaya Selangor Tel +603-8688 1900 Fax +603-8688 1911 Email [email protected] Website www.mqa.gov.my © Malaysian Qualifications Agency 2020 All the Agency’s publications are available on our portal: www.mqa.gov.my ii CONTENTS Page FOREWORD i ABBREVIATIONS iii 1. INTRODUCTION 1 2. PROGRAMME DEVELOPMENT AND DELIVERY 4 2.1 PROGRAMME EDUCATIONAL OBJECTIVES 4 2.2 LEARNING OUTCOMES 8 2.3 CURRICULUM DESIGN AND DELIVERY 21 3. ASSESSMENT OF STUDENT LEARNING 33 4. STUDENT SELECTION 36 5. ACADEMIC STAFF 40 6. EDUCATIONAL RESOURCES 46 7. PROGRAMME MANAGEMENT 47 8. PROGRAMME MONITORING, REVIEW AND CONTINUAL QUALITY 49 IMPROVEMENT REFERENCES 51 APPENDICES APPENDIX 1: LIST OF PANEL MEMBERS 53 APPENDIX 2: LIST OF ORGANISATIONS INVOLVED IN THE 54 STAKEHOLDERS WORKSHOPS APPENDIX 3 BODY OF KNOWLEDGE 56 APPENDIX 4: EXAMPLES OF NOMENCLATURES 63 APPENDIX 5: AREAS OF EMPLOYMENT 65 APPENDIX 6: HALAL WORK ACTIVITIES CHECKLIST FOR 66 INDUSTRIAL TRAINING GLOSSARY 68 iii FOREWORD In its effort to ensure that the programmes offered by Higher Education Providers (HEPs) in Malaysia meet the acceptable level of quality, the Malaysian Qualifications Agency (MQA) has published numerous quality assurance documents such as the Malaysian Qualifications Framework (MQF), Code of Practice for Programme Accreditation (COPPA), Code of Practice for Institutional Audit (COPIA), Code of Practice for TVET Programme Accreditation (COPTPA), Code of Practice for Programme Accreditation Open Distance Learning (COPPA- ODL), Standards, Programme Standards (PS) and Guidelines to Good Practices (GGP).
    [Show full text]
  • Curriculum Vitae
    CURRICULUM VITAE ASSOC. PROF. DR. NOOR SYAMILAH ZAKARIA, K.B., P.A. Department of Counselor Education and Counseling Psychology Faculty of Educational Studies Universiti Putra Malaysia 43400 UPM Serdang Selangor Darul Ehsan, Malaysia T: 603-9769 8190 E: [email protected] 1 PERSONAL DETAILS Full Name Dr. Noor Syamilah Zakaria Staff Number A04219 Position Profesor Madya Nationality Malaysian Areas of Counselor education and supervision; Guidance and counseling; Specialization Counseling ethics education; Teacher education [email protected] E-mail [email protected] Telephone 603-8946 8190 Fax 603-8946 8142 Handphone 6012-784 9776 BIODATA Dr. Noor Syamilah Zakaria was born on 13 May 1980 in Kota Bharu, Kelantan. She is a Registered Counselor (00546) and Certified Counseling Practitioner (00604) with the Board of Counselors (Malaysia). She received her early primary education at Sekolah Kebangsaan Ketereh, Kota Bharu, Kelantan; and secondary level education at Sekolah Seri Puteri, Jalan Kolam Ayer, Kuala Lumpur. She graduated with a Bachelor of Education (Guidance and Counseling) in 2002 and a Master of Education (Guidance and Counseling) in 2007, both at the Universiti Putra Malaysia. From 2002 through 2008, she was employed by the Ministry of Education Malaysia as a School Counselor at two public secondary schools in the district of Petaling, Selangor. In September 2008, she became a Tutor with the Universiti Putra Malaysia and pursued her doctoral degree with the scholarship awarded by the Ministry of Higher Education Malaysia and the Universiti Putra Malaysia from August 2009 through August 2013 at the University of Wyoming, USA. On 11 May 2013, she graduated with a Ph.D.
    [Show full text]
  • Scholarship Programme
    Scholarship Programme 1 FWD Takaful Scholarship Programme About FWD Takaful FWD Takaful Berhad (“FWD Takaful”) is a Takaful provider in Malaysia that offers family Takaful services. FWD Takaful is licensed under the Islamic Financial Services Act 2013 and is regulated by Bank Negara Malaysia. It is a Takaful business unit of FWD Group (“FWD”) – which spans Hong Kong & Macau, Thailand, Indonesia, the Philippines, Singapore, Vietnam, Japan and Malaysia; offering life and medical insurance, general insurance, employee benefits, Shariah and family Takaful products across a number of its markets. FWD is focused on creating fresh customer experiences and making the insurance journey simpler, faster and smoother, with innovative propositions and easy-to-understand products, supported by digital technology. Through this customer-led approach, FWD aims to become a leading pan-Asian insurer that changes the way people feel about insurance. Established in Asia in 2013 with a trailblazer mentality, FWD is the primary insurance business of investment group, Pacific Century Group. For more information, please visitfwd.com.my. 1 FWD Takaful Scholarship Programme FWD Takaful Scholarship Programme FWD Takaful is offering scholarship opportunities to deserving Malaysian students, from B40 family or those whose household income is below RM5000 who need financial aid to pursue their education at institutions of higher learning. This is a full scholarship programme that will fully fund a 4-year study programme (including pre-university for SPM holders) at stipulated universities. The scholarship aims to develop the students who are excel in their studies to have further skills and knowledge. We're promoting and encouraging these students to take up study in the fields of Takaful/Insurance, Shariah, Islamic Finance/Finance, Information Technology and Actuarial Science.
    [Show full text]
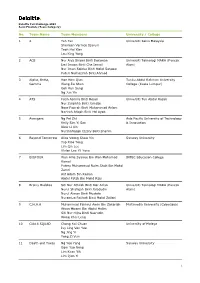
  • No. Team Name Team Members University / College
    Deloitte Tax Challenge 2019 Semi-Finalists (Team Category) No. Team Name Team Members University / College 1 4 Teh Yen Universiti Sains Malaysia Sherleen Vernice Djarum Teoh Hui Xian Lau King Yong 2 ACE Nur Alya Ilhami Binti Deraman Universiti Teknologi MARA (Puncak Izni Imaan Binti Che Ismail Alam) Nur Iman Soleha Binti Mohd Safawai Puteri Nurhazirah Binti Ahmad 3 Alpha, Betta, Hoe Wen Qian Tunku Abdul Rahman University Gamma Wang Jia Shun College (Kuala Lumpur) Goh Ken Seng Ng Jun Yin 4 ATS Fatin Asmira Binti Roseli Universiti Tun Abdul Razak Nur Zulaikha Binti Jamdan Noor Fazirah Binti Muhammad Aslam Nazirah Atiqah Binti Md Ayob 5 Avengers Ng Pei Zhi Asia Pacific University of Technology Kelly Sim Yi San & Innovation Kiew Li Xin Nurshafiqqah Izzaty Binti Sharim 6 Beyond Tomorrow Alice Voong Shew Yin Sunway University Yap Xiao Tong Lim Qin Lee Vivien Lee Yii Yune 7 BIGFOUR Wan Alfie Syairee Bin Wan Mohamad INTEC Education College Kamal Putera Muhammad Naim Shah Bin Mohd Zamri Alif Adam Bin Roslan Abdul Fatah Bin Mohd Rais 8 Brainy Buddies Siti Nur Athilah Binti Nor Azlan Universiti Teknologi MARA (Puncak Nurul Shafiqah Binti Jaladudin Alam) Nurul Aiman Binti Mustafa Nuramiza Fatihah Binti Mohd Zailani 9 C.H.A.A Muhammad Fakhrul Amin Bin Zakariah Multimedia University (Cyberjaya) Afnan Hizami Bin Abdul Halim Siti Nur Hijra Binti Nasrudin Wong Chei Leng 10 CIA16 SQUAD Chong Kai Chuan University of Malaya Ivy Ling Ven Yee Ng Jing Yi Yong Zi Vun 11 Death and Taxes Ng Yee Yang Sunway University Gam Yao Neng Lim Kean Yik Lim Qian Yi 1 Deloitte Tax Challenge 2019 Semi-Finalists (Team Category) No.
    [Show full text]
  • Annual Report
    ANNUAL REPORT 31 December 2014 © SACE Board of South Australia ABN 87 604 513 459 ISBN 978 1 74102 789 1 (online version) ISBN 978 1 74102 790 7 (printed version) ISSN 0815–2004 Prepared by the Communications Group SACE Board of South Australia 60 Greenhill Road Wayville South Australia 5034 Telephone: +61 8 8372 7400 Facsimile: +61 8 8372 7590 Email: [email protected] Website Address: www.sace.sa.edu.au South Australian Certificate of Education 60 Greenhill Road Wayville SA 5034 Phone +61 8 8372 7400 Fax +61 8 8372 7590 [email protected] www.sace.sa.edu.au ABN 87 604 513 459 Monday 30 March 2015 To the Honourable Susan Close MP Minister for Education and Child Development Dear Minister I am pleased to submit the 2014 Annual Report of the SACE Board of South Australia, in accordance with the SACE Board of South Australia Act 1983 and the Department of the Premier and Cabinet Circular, PC013 — Annual Reporting Requirements (2014). This report documents the activities and achievements of the SACE Board of South Australia for the period 1 January 2014 to 31 December 2014. Yours sincerely Jane Danvers Presiding Member of the Board SACE Board of South Australia CONTENTS Presiding Member’s Statement 1 Chief Executive’s Statement 4 The SACE Board of South Australia 6 Strategic Plan 2012–16 10 Curriculum, Assessment, and Standards 12 SACE Curriculum 12 Board-recognised Courses 15 Assessment and Standards 16 SACE as a Best Practice Qualification 19 SACE Directions and Actions 19 Providing the SACE to International Communities 20 Continuous
    [Show full text]
  • FSI Education Roadshow March 2018 Overall Statistics
    FSI Education Roadshow March 2018 Overall Statistics North City Alor Setar Ipoh Perai Penang Venue Star City Syeun Hotel Ixora Hotel Jen Hotel Date 16-Mar 19-Mar 20-Mar 21-Mar Number of Visitor 800 1000 1000 600 Number of Exhibitor 34 48 45 42 Southern City Seremban Kluang Johor Johor Melaka Venue Klana Resort Prime City Hotel Holiday Villa Holiday Villa Equatorial Date 23-Mar 24-Mar 25-Mar 26-Mar 27-Mar Number of Visitor 350 300 1000 400 400 Number of Exhibitor 24 30 64 56 40 Grand Total: Number of Visitor 5050 Number of Exhibitor 81 FSI Education Roadshow Mar 2018 - Exhibitors' Feedback Jen Hotel Klana Resort Prime City Holiday Villa Holiday Villa Hotel Venue ALOR SETAR IPOH SEBERANG PENANG SEREMBAN KLUANG JOHOR JOHOR MELAKA Day 1 Day 2 Total Exhibitor 34 51 47 42 24 30 61 56 42 Total Feedback 30 33 44 34 24 29 52 44 31 No. (%) No. (%) No. (%) No. (%) No. (%) No. (%) No. (%) No. (%) No. (%) 1. Flow of visitors Excellent 6 17.65 3 5.88 8 17.02 3 7.14 0 0.00 0 0.00 19 31.15 1 1.79 2 4.76 Good 14 41.18 12 23.53 27 57.45 8 19.05 12 50.00 6 20.00 30 49.18 16 28.57 5 11.90 Fair 10 29.41 17 33.33 7 14.89 16 38.10 11 45.83 12 40.00 2 3.28 19 33.93 17 40.48 Poor 0 0.00 1 1.96 0 0.00 4 9.52 1 4.17 11 36.67 1 1.64 8 14.29 7 16.67 No Respond 4 11.76 18 35.29 5 10.64 11 26.19 0 0.00 1 3.33 9 14.75 12 21.43 11 26.19 2.
    [Show full text]