DOCSLIB.ORG

Triangle Centres and Homogeneous Coordinates

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Triangle Centres and Homogeneous Coordinates A A E E F I Triangle Centres F H and Homogeneous B D C B D C Figure 1. Incentre of a triangle; Coordinates I is equidistant from the sides Figure 3. Orthocentre of an acute-angled triangle ClassRoom Incentre. Since the incentre is equidistant from them. So the reciprocals of the sides bear the same Part I - Trilinear Coordinates the sides, its trilinear coordinates are simply ratios to each other as the cosecant values. 1 : 1 : 1 (see Figure 1). Orthocentre. Now we turn our attention to the Centroid. Let G be the centroid of ABC (see orthocentre. We first consider the case ofan △ Figure 2). It is a well-known result of Euclidean acute-angled triangle ABC (see Figure 3). Here, geometry that triangles GAB, GBC and GCA are AD, BE, CF are perpendiculars from the vertices equal in area. If GD, GE and GF are A, B, C to the sides BC, CA, AB, respectively; H is perpendiculars to the sides, then GD a/2 = the orthocentre. · A Ramachandran GE b/2 = GF c/2 = k, say. Since HCD = 90◦ B, we get DHC = B, uring a course in Euclidean geometry at high school level, · · − GD = k/a GE = k/b GF = and sec B = HC/HD. Similarly, HCE = 90◦ a student encounters four classical triangle centres—the This yields: 2 , 2 , − / : : = / : / : / A, so EHC = A, and sec A = HC/HE. circumcentre, the incentre, the orthocentre and the 2k c, hence GD GE GF 1 a 1 b 1 c; Hence: Dcentroid (introduced as the points of concurrence of the these ratios form the trilinear coordinates of the centroid. HD HC HC sec A perpendicular bisectors of the sides, the bisectors of the angles of the = / = . triangle, the altitudes and the medians, respectively). We shall study Alternatively, the coordinates could be given as bc : HE HE HD sec C two alternative ways of describing and characterising these four ca : ab (multiplying through by abc), or as csc A : Similarly, HE/HF = sec B/sec C. Therefore the significant points. They are both known as homogeneous coordinate csc B : csc C. The last relation arises from the fact trilinear coordinates of the orthocentre are sec A : systems, but we explain the significance of this term later. In part Iof that the sides of a triangle bear the same ratios to sec B : sec C. the article, we consider the first of these: trilinear coordinates. each other as the sines of the angles opposite Let us see what happens as one of the angles (say A) approaches 90◦. The other two angles also Trilinear coordinates A approach limiting values which we assume are This approach was suggested by the German physicist-mathematician distinct from 0◦ and 90◦. Note that HE/HD = Julius Plücker in 1835 [1]. Here a triangle centre is characterised in cos A/cos B and HF/HD = cos A/cos C. As terms of its perpendicular distances from the three sides of the A 90◦, cos A 0; so HE 0 and HF 0 E → → → → triangle; or rather, the ratios of these distances. These ratios form the (in the limit, A, H, E, F coincide; see Figure 4). “trilinear coordinates” of the triangle centre. If ABC is the triangle F Two of the three quantities HD, HE, HF are now △ G and P the point in question, then the perpendicular distances zero, and it is customary to write the ratios as PD, PE, PF to the sides BC, CA, AB respectively are expressed as HD : HE : HF = 1 : 0 : 0. ratios involving the side lengths and/or trigonometric functions of the angles of the triangle. B D C It follows that for a right-angled triangle ABC with A = 90◦, the trilinear coordinates of the Figure 2. Centroid of an arbitrary triangle orthocentre are 1 : 0 : 0. Keywords: Triangle centre, incentre, centroid, orthocentre, circumcentre, trilinear coordinates, homogeneous coordinates, trigonometric ratio 4140 At Right Angles | Vol. 5, No. 1, March 2016 Vol. 5, No. 1, March 2016 | At Right Angles 4140 1 A A E E F I Triangle Centres F H and Homogeneous B D C B D C Figure 1. Incentre of a triangle; Coordinates I is equidistant from the sides Figure 3. Orthocentre of an acute-angled triangle ClassRoom Incentre. Since the incentre is equidistant from them. So the reciprocals of the sides bear the same Part I - Trilinear Coordinates the sides, its trilinear coordinates are simply ratios to each other as the cosecant values. 1 : 1 : 1 (see Figure 1). Orthocentre. Now we turn our attention to the Centroid. Let G be the centroid of ABC (see orthocentre. We first consider the case ofan △ Figure 2). It is a well-known result of Euclidean acute-angled triangle ABC (see Figure 3). Here, geometry that triangles GAB, GBC and GCA are AD, BE, CF are perpendiculars from the vertices equal in area. If GD, GE and GF are A, B, C to the sides BC, CA, AB, respectively; H is perpendiculars to the sides, then GD a/2 = the orthocentre. · A Ramachandran GE b/2 = GF c/2 = k, say. Since HCD = 90◦ B, we get DHC = B, uring a course in Euclidean geometry at high school level, · · − GD = k/a GE = k/b GF = and sec B = HC/HD. Similarly, HCE = 90◦ a student encounters four classical triangle centres—the This yields: 2 , 2 , − / : : = / : / : / A, so EHC = A, and sec A = HC/HE. circumcentre, the incentre, the orthocentre and the 2k c, hence GD GE GF 1 a 1 b 1 c; Hence: Dcentroid (introduced as the points of concurrence of the these ratios form the trilinear coordinates of the centroid. HD HC HC sec A perpendicular bisectors of the sides, the bisectors of the angles of the = / = . triangle, the altitudes and the medians, respectively). We shall study Alternatively, the coordinates could be given as bc : HE HE HD sec C two alternative ways of describing and characterising these four ca : ab (multiplying through by abc), or as csc A : Similarly, HE/HF = sec B/sec C. Therefore the significant points. They are both known as homogeneous coordinate csc B : csc C. The last relation arises from the fact trilinear coordinates of the orthocentre are sec A : systems, but we explain the significance of this term later. In part Iof that the sides of a triangle bear the same ratios to sec B : sec C. the article, we consider the first of these: trilinear coordinates. each other as the sines of the angles opposite Let us see what happens as one of the angles (say A) approaches 90◦. The other two angles also Trilinear coordinates A approach limiting values which we assume are This approach was suggested by the German physicist-mathematician distinct from 0◦ and 90◦. Note that HE/HD = Julius Plücker in 1835 [1]. Here a triangle centre is characterised in cos A/cos B and HF/HD = cos A/cos C. As terms of its perpendicular distances from the three sides of the A 90◦, cos A 0; so HE 0 and HF 0 E → → → → triangle; or rather, the ratios of these distances. These ratios form the (in the limit, A, H, E, F coincide; see Figure 4). “trilinear coordinates” of the triangle centre. If ABC is the triangle F Two of the three quantities HD, HE, HF are now △ G and P the point in question, then the perpendicular distances zero, and it is customary to write the ratios as PD, PE, PF to the sides BC, CA, AB respectively are expressed as HD : HE : HF = 1 : 0 : 0. ratios involving the side lengths and/or trigonometric functions of the angles of the triangle. B D C It follows that for a right-angled triangle ABC with A = 90◦, the trilinear coordinates of the Figure 2. Centroid of an arbitrary triangle orthocentre are 1 : 0 : 0. Keywords: Triangle centre, incentre, centroid, orthocentre, circumcentre, trilinear coordinates, homogeneous coordinates, trigonometric ratio 4140 At Right Angles | Vol. 5, No. 1, March 2016 Vol. 5, No. 1, March 2016 | At Right Angles 4140 1 A, H, E, F A A A F E F E E F B D C O B D C B D, O C O Figure 4. Orthocentre of a right-angled triangle Figure 7. Circumcentre of a right-angled triangle Figure 8. Circumcentre of an obtuse-angled triangle H B D C F obtained earlier; only, cos A has now assumed a Note from the editor: What is homogeneous zero value. about this system? The significance of the term In the case of an obtuse-angled triangle, the homogeneous may not be immediately apparent. In Figure 6. Circumcentre of an acute-angled triangle circumcentre O lies outside the triangle (see ‘ordinary’ coordinate geometry, the equation of a E + + = , , Figure 8, where A is obtuse). line has the form ax by c 0, where a b c A are constants. Note that this equation is not and we find that the inherent symmetry ofthe Here we have BOD = 180◦ A, so OD = − homogeneous: two terms have degree 1, while one formula has been restored. R cos A. The relations OE = R cos B and OF = − term has degree 0. Similarly, the question of a B D C R cos C remain unchanged. So we get OD : OE : circle has the form x2 + y2 + 2gx + 2fy + c = 0; Circumcentre. Next, we consider the OF = cos A : cos B : cos C. If we adopt the this too is not homogeneous. In some settings, it Figure 5. Orthocentre of an obtuse-angled triangle − circumcentre.
Load more

Recommended publications
  • Angle Chasing
    Angle Chasing Ray Li June 12, 2017 1 Facts you should know 1. Let ABC be a triangle and extend BC past C to D: Show that \ACD = \BAC + \ABC: 2. Let ABC be a triangle with \C = 90: Show that the circumcenter is the midpoint of AB: 3. Let ABC be a triangle with orthocenter H and feet of the altitudes D; E; F . Prove that H is the incenter of 4DEF . 4. Let ABC be a triangle with orthocenter H and feet of the altitudes D; E; F . Prove (i) that A; E; F; H lie on a circle diameter AH and (ii) that B; E; F; C lie on a circle with diameter BC. 5. Let ABC be a triangle with circumcenter O and orthocenter H: Show that \BAH = \CAO: 6. Let ABC be a triangle with circumcenter O and orthocenter H and let AH and AO meet the circumcircle at D and E, respectively. Show (i) that H and D are symmetric with respect to BC; and (ii) that H and E are symmetric with respect to the midpoint BC: 7. Let ABC be a triangle with altitudes AD; BE; and CF: Let M be the midpoint of side BC. Show that ME and MF are tangent to the circumcircle of AEF: 8. Let ABC be a triangle with incenter I, A-excenter Ia, and D the midpoint of arc BC not containing A on the circumcircle. Show that DI = DIa = DB = DC: 9. Let ABC be a triangle with incenter I and D the midpoint of arc BC not containing A on the circumcircle.
    [Show full text]
  • Control Point Based Representation of Inellipses of Triangles∗
    Annales Mathematicae et Informaticae 40 (2012) pp. 37–46 http://ami.ektf.hu Control point based representation of inellipses of triangles∗ Imre Juhász Department of Descriptive Geometry, University of Miskolc, Hungary [email protected] Submitted April 12, 2012 — Accepted May 20, 2012 Abstract We provide a control point based parametric description of inellipses of triangles, where the control points are the vertices of the triangle themselves. We also show, how to convert remarkable inellipses defined by their Brianchon point to control point based description. Keywords: inellipse, cyclic basis, rational trigonometric curve, Brianchon point MSC: 65D17, 68U07 1. Introduction It is well known from elementary projective geometry that there is a two-parameter family of ellipses that are within a given non-degenerate triangle and touch its three sides. Such ellipses can easily be constructed in the traditional way (by means of ruler and compasses), or their implicit equation can be determined. We provide a method using which one can determine the parametric form of these ellipses in a fairly simple way. Nowadays, in Computer Aided Geometric Design (CAGD) curves are repre- sented mainly in the form n g (u) = j=0 Fj (u) dj δ Fj :[a, b] R, u [a, b] R, dj R , δ 2 P→ ∈ ⊂ ∈ ≥ ∗This research was carried out as a part of the TAMOP-4.2.1.B-10/2/KONV-2010-0001 project with support by the European Union, co-financed by the European Social Fund. 37 38 I. Juhász where dj are called control points and Fj (u) are blending functions. (The most well-known blending functions are Bernstein polynomials and normalized B-spline basis functions, cf.
    [Show full text]
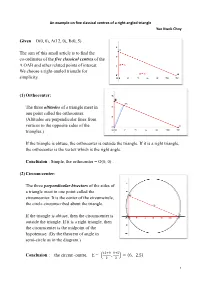
  • An Example on Five Classical Centres of a Right Angled Triangle
    An example on five classical centres of a right angled triangle Yue Kwok Choy Given O(0, 0), A(12, 0), B(0, 5) . The aim of this small article is to find the co-ordinates of the five classical centres of the ∆ OAB and other related points of interest. We choose a right-angled triangle for simplicity. (1) Orthocenter: The three altitudes of a triangle meet in one point called the orthocenter. (Altitudes are perpendicular lines from vertices to the opposite sides of the triangles.) If the triangle is obtuse, the orthocenter is outside the triangle. If it is a right triangle, the orthocenter is the vertex which is the right angle. Conclusion : Simple, the orthocenter = O(0, 0) . (2) Circum-center: The three perpendicular bisectors of the sides of a triangle meet in one point called the circumcenter. It is the center of the circumcircle, the circle circumscribed about the triangle. If the triangle is obtuse, then the circumcenter is outside the triangle. If it is a right triangle, then the circumcenter is the midpoint of the hypotenuse. (By the theorem of angle in semi-circle as in the diagram.) Conclusion : the circum -centre, E = ͥͦͮͤ ͤͮͩ ʠ ͦ , ͦ ʡ Ɣ ʚ6, 2.5ʛ 1 Exercise 1: (a) Check that the circum -circle above is given by: ͦ ͦ ͦ. ʚx Ǝ 6ʛ ƍ ʚy Ǝ 2.5ʛ Ɣ 6.5 (b) Show that t he area of the triangle with sides a, b, c and angles A, B, C is ΏΐΑ ͦ , where R is the radius of the circum -circle .
    [Show full text]
  • Chapter 1. the Medial Triangle 2
    Chapter 1. The Medial Triangle 2 The triangle formed by joining the midpoints of the sides of a given triangle is called the me- dial triangle. Let A1B1C1 be the medial trian- gle of the triangle ABC in Figure 1. The sides of A1B1C1 are parallel to the sides of ABC and 1 half the lengths. So A B C is the area of 1 1 1 4 ABC. Figure 1: In fact area(AC1B1) = area(A1B1C1) = area(C1BA1) 1 = area(B A C) = area(ABC): 1 1 4 Figure 2: The quadrilaterals AC1A1B1 and C1BA1B1 are parallelograms. Thus the line segments AA1 and C1B1 bisect one another, and the line segments BB1 and CA1 bisect one another. (Figure 2) Figure 3: Thus the medians of A1B1C1 lie along the medians of ABC, so both tri- angles A1B1C1 and ABC have the same centroid G. 3 Now draw the altitudes of A1B1C1 from vertices A1 and C1. (Figure 3) These altitudes are perpendicular bisectors of the sides BC and AB of the triangle ABC so they intersect at O, the circumcentre of ABC. Thus the orthocentre of A1B1C1 coincides with the circumcentre of ABC. Let H be the orthocentre of the triangle ABC, that is the point of intersection of the altitudes of ABC. Two of these altitudes AA2 and BB2 are shown. (Figure 4) Since O is the orthocen- tre of A1B1C1 and H is the orthocentre of ABC then jAHj = 2jA1Oj Figure 4: . The centroid G of ABC lies on AA1 and jAGj = 2jGA1j . We also have AA2kOA1, since O is the orthocentre of A1B1C1.
    [Show full text]
  • The Vertex-Midpoint-Centroid Triangles
    Forum Geometricorum b Volume 4 (2004) 97–109. bbb FORUM GEOM ISSN 1534-1178 The Vertex-Midpoint-Centroid Triangles Zvonko Cerinˇ Abstract. This paper explores six triangles that have a vertex, a midpoint of a side, and the centroid of the base triangle ABC as vertices. They have many in- teresting properties and here we study how they monitor the shape of ABC. Our results show that certain geometric properties of these six triangles are equivalent to ABC being either equilateral or isosceles. Let A, B, C be midpoints of the sides BC, CA, AB of the triangle ABC and − let G be its centroid (i.e., the intersection of medians AA, BB , CC ). Let Ga , + − + − + Ga , Gb , Gb , Gc , Gc be triangles BGA , CGA , CGB , AGB , AGC , BGC (see Figure 1). C − + Gb Ga B A G + − Gb Ga − + Gc Gc ABC Figure 1. Six vertex–midpoint–centroid triangles of ABC. This set of six triangles associated to the triangle ABC is a special case of the cevasix configuration (see [5] and [7]) when the chosen point is the centroid G.It has the following peculiar property (see [1]). Theorem 1. The triangle ABC is equilateral if and only if any three of the trian- = { − + − + − +} gles from the set σG Ga ,Ga ,Gb ,Gb ,Gc ,Gc have the same either perime- ter or inradius. In this paper we wish to show several similar results. The idea is to replace perimeter and inradius with other geometric notions (like k-perimeter and Brocard angle) and to use various central points (like the circumcenter and the orthocenter – see [4]) of these six triangles.
    [Show full text]
  • Arxiv:2101.02592V1 [Math.HO] 6 Jan 2021 in His Seminal Paper [10]
    International Journal of Computer Discovered Mathematics (IJCDM) ISSN 2367-7775 ©IJCDM Volume 5, 2020, pp. 13{41 Received 6 August 2020. Published on-line 30 September 2020 web: http://www.journal-1.eu/ ©The Author(s) This article is published with open access1. Arrangement of Central Points on the Faces of a Tetrahedron Stanley Rabinowitz 545 Elm St Unit 1, Milford, New Hampshire 03055, USA e-mail: [email protected] web: http://www.StanleyRabinowitz.com/ Abstract. We systematically investigate properties of various triangle centers (such as orthocenter or incenter) located on the four faces of a tetrahedron. For each of six types of tetrahedra, we examine over 100 centers located on the four faces of the tetrahedron. Using a computer, we determine when any of 16 con- ditions occur (such as the four centers being coplanar). A typical result is: The lines from each vertex of a circumscriptible tetrahedron to the Gergonne points of the opposite face are concurrent. Keywords. triangle centers, tetrahedra, computer-discovered mathematics, Eu- clidean geometry. Mathematics Subject Classification (2020). 51M04, 51-08. 1. Introduction Over the centuries, many notable points have been found that are associated with an arbitrary triangle. Familiar examples include: the centroid, the circumcenter, the incenter, and the orthocenter. Of particular interest are those points that Clark Kimberling classifies as \triangle centers". He notes over 100 such points arXiv:2101.02592v1 [math.HO] 6 Jan 2021 in his seminal paper [10]. Given an arbitrary tetrahedron and a choice of triangle center (for example, the circumcenter), we may locate this triangle center in each face of the tetrahedron.
    [Show full text]
  • The Uses of Homogeneous Barycentric Coordinates in Plane Euclidean Geometry by PAUL
    The uses of homogeneous barycentric coordinates in plane euclidean geometry by PAUL YIU Department of Mathematical Sciences, Florida Atlantic University, Boca Raton, FL 33431, USA The notion of homogeneous barycentric coordinates provides a pow- erful tool of analysing problems in plane geometry. In this paper, we explain the advantages over the traditional use of trilinear coordinates, and illustrate its powerfulness in leading to discoveries of new and in- teresting collinearity relations of points associated with a triangle. 1. Introduction In studying geometric properties of the triangle by algebraic methods, it has been customary to make use of trilinear coordinates. See, for examples, [3, 6, 7, 8, 9]. With respect to a ¯xed triangle ABC (of side lengths a, b, c, and opposite angles ®, ¯, °), the trilinear coordinates of a point is a triple of numbers proportional to the signed distances of the point to the sides of the triangle. The late Jesuit mathematician Maurice Wong has given [9] a synthetic construction of the point with trilinear coordinates cot ® : cot ¯ : cot °, and more generally, in [8] points with trilinear coordinates a2nx : b2ny : c2nz from one with trilinear coordinates x : y : z with respect to a triangle with sides a, b, c. On a much grandiose scale, Kimberling [6, 7] has given extensive lists of centres associated with a triangle, in terms of trilinear coordinates, along with some collinearity relations. The present paper advocates the use of homogeneous barycentric coor- dinates instead. The notion of barycentric coordinates goes back to MÄobius. See, for example, [4]. With respect to a ¯xed triangle ABC, we write, for every point P on the plane containing the triangle, 1 P = (( P BC)A + ( P CA)B + ( P AB)C); ABC 4 4 4 4 and refer to this as the barycentric coordinate of P .
    [Show full text]
  • Applications of Trilinear Coordinates to Some
    APPLICATIONS OF TRILINEAR COORDINATES TO SOME PROBLEMS IN PLANE ELASTICITY Ramanath Williams Thesis submitted to the Graduate Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE in Engineering Mechanics l\l'PROVED: H. F. Brinson, Chairman --------------- tl.-~:.J C. W. Smith R. P. McNit ... D. Frederick, Department Head October, 1972 Blacksburg, Virginia ACKNOWLEDGMENTS The author wishes to express his sincere thanks to Professor H. F. Brinson of the Department of Engineering Science and Mechanics, Virginia Polytechni.c Institute and State University, for his helpful criticisms and encouragement during the course of this investigation. The author is also grateful to the Department of Defense who sponsored this work under Project Themis, Contract Number DAA-F07-69-C-0444 with Watervliet Arsenal, Watervliet, New York. Finally, thanks are due to Mrs. Peggy Epperly for typing this manuscript. TABLE OF CONTENTS Section LIST OF ILLUSTRATIONS v LIST OF SYMBOLS vi INTRODUCTION • . 1 l. DEFINITION OF TRILINEAR COORDINATES • 6 2. RELATIONSHIP BETWEEN CARTESIAN Ai.~D TRILINEAR COORDINATES 9 3, TRIAXIAL STRESS SYSTEM 16 ,~, STRESS-STFAIN RELATIONS IN TERMS OF TRIAXIAL STRESS AND STRAIN COMPONENTS . 22 5. RELATIONSHIP BETWEEN THE STATE OF STRESS AND STRAIN IN THE CARTESIAN AND TRIAXIAL COORDINATES . 27 6. :PRINCIPAL STRESSES AND STRAIN ENE.RGY OF DEFORMATION . 34 7. SOME EQUATIONS OF PLANE ELASTICITY 38 7 .1 Equilibrium equations 38 7.2 Kinematics and compatibility equation 46 7.3 Governing equations of thin plate 54 7 ,lf Boundary conditions for a triangular plate 59 8. INTEGRATION OF A FUNCTION COMPOSED OF TRILINEAR VARIABLES 63 9.
    [Show full text]
  • Lemmas in Euclidean Geometry1 Yufei Zhao [email protected]
    IMO Training 2007 Lemmas in Euclidean Geometry Yufei Zhao Lemmas in Euclidean Geometry1 Yufei Zhao [email protected] 1. Construction of the symmedian. Let ABC be a triangle and Γ its circumcircle. Let the tangent to Γ at B and C meet at D. Then AD coincides with a symmedian of △ABC. (The symmedian is the reflection of the median across the angle bisector, all through the same vertex.) A A A O B C M B B F C E M' C P D D Q D We give three proofs. The first proof is a straightforward computation using Sine Law. The second proof uses similar triangles. The third proof uses projective geometry. First proof. Let the reflection of AD across the angle bisector of ∠BAC meet BC at M ′. Then ′ ′ sin ∠BAM ′ ′ BM AM sin ∠ABC sin ∠BAM sin ∠ABD sin ∠CAD sin ∠ABD CD AD ′ = ′ sin ∠CAM ′ = ∠ ∠ ′ = ∠ ∠ = = 1 M C AM sin ∠ACB sin ACD sin CAM sin ACD sin BAD AD BD Therefore, AM ′ is the median, and thus AD is the symmedian. Second proof. Let O be the circumcenter of ABC and let ω be the circle centered at D with radius DB. Let lines AB and AC meet ω at P and Q, respectively. Since ∠PBQ = ∠BQC + ∠BAC = 1 ∠ ∠ ◦ 2 ( BDC + DOC) = 90 , we see that PQ is a diameter of ω and hence passes through D. Since ∠ABC = ∠AQP and ∠ACB = ∠AP Q, we see that triangles ABC and AQP are similar. If M is the midpoint of BC, noting that D is the midpoint of QP , the similarity implies that ∠BAM = ∠QAD, from which the result follows.
    [Show full text]
  • Triangle-Centers.Pdf
    Triangle Centers Maria Nogin (based on joint work with Larry Cusick) Undergraduate Mathematics Seminar California State University, Fresno September 1, 2017 Outline • Triangle Centers I Well-known centers F Center of mass F Incenter F Circumcenter F Orthocenter I Not so well-known centers (and Morley's theorem) I New centers • Better coordinate systems I Trilinear coordinates I Barycentric coordinates I So what qualifies as a triangle center? • Open problems (= possible projects) mass m mass m mass m Centroid (center of mass) C Mb Ma Centroid A Mc B Three medians in every triangle are concurrent. Centroid is the point of intersection of the three medians. mass m mass m mass m Centroid (center of mass) C Mb Ma Centroid A Mc B Three medians in every triangle are concurrent. Centroid is the point of intersection of the three medians. Centroid (center of mass) C mass m Mb Ma Centroid mass m mass m A Mc B Three medians in every triangle are concurrent. Centroid is the point of intersection of the three medians. Incenter C Incenter A B Three angle bisectors in every triangle are concurrent. Incenter is the point of intersection of the three angle bisectors. Circumcenter C Mb Ma Circumcenter A Mc B Three side perpendicular bisectors in every triangle are concurrent. Circumcenter is the point of intersection of the three side perpendicular bisectors. Orthocenter C Ha Hb Orthocenter A Hc B Three altitudes in every triangle are concurrent. Orthocenter is the point of intersection of the three altitudes. Euler Line C Ha Hb Orthocenter Mb Ma Centroid Circumcenter A Hc Mc B Euler line Theorem (Euler, 1765).
    [Show full text]
  • 1. EUCLIDEAN GEOMETRY 1.3. Triangle Centres
    1. EUCLIDEAN GEOMETRY 1.3. Triangle Centres Triangle Centres The humble triangle, with its three vertices and three sides, is actually a very remarkable object. For evidence of this fact, just look at the Encyclopedia of Triangle Centers1 on the internet, which catalogues literally thousands of special points that every triangle has. We’ll only be looking at the big four — namely, the circumcentre, the incentre, the orthocentre, and the centroid. While exploring these constructions, we’ll need all of our newfound geometric knowledge from the previous lecture, so let’s have a quick recap. Triangles – Congruence : There are four simple rules to determine whether or not two triangles are congruent. They are SSS, SAS, ASA and RHS. – Similarity : There are also three simple rules to determine whether or not two triangles are similar. They are AAA, PPP and PAP. – Midpoint Theorem : Let ABC be a triangle where the midpoints of the sides BC, CA, AB are X, Y, Z, respectively. Then the four triangles AZY, ZBX, YXC and XYZ are all congruent to each other and similar to triangle ABC. Circles – The diameter of a circle subtends an angle of 90◦. In other words, if AB is the diameter of a circle and C is a point on the circle, then \ACB = 90◦. – The angle subtended by a chord at the centre is twice the angle subtended at the circumference, on the same side. In other words, if AB is a chord of a circle with centre O and C is a point on the circle on the same side of AB as O, then \AOB = 2\ACB.
    [Show full text]
  • Singularities of Centre Symmetry Sets 1 Introduction
    Singularities of centre symmetry sets P.J.Giblin, V.M.Zakalyukin 1 1 Introduction We study the singularities of envelopes of families of chords (special straight lines) intrin- sically related to a hypersurface M ⊂ Rn embedded into an affine space. The origin of this investigation is the paper [10] of Janeczko. He described a general- ization of central symmetry in which a single point—the centre of symmetry—is replaced by the bifurcation set of a certain family of ratios. In [6] Giblin and Holtom gave an alternative description, as follows. For a hypersurface M ⊂ Rn we consider pairs of points at which the tangent hy- perplanes are parallel, and in particular take the family of chords (regarded as infinite lines) joining these pairs. For n = 2 these chords will always have an envelope, and this envelope is called the centre symmetry set (CSS) of the curve M. When M is convex (the case considered in [10]) the envelope is quite simple to describe, and has cusps as its only generic singularities. In [6] the case when M is not convex is considered, and there the envelope acquires extra components, and singularities resembling boundary singularities of Arnold. This is because, arbitrarily close to an ordinary inflexion, there are pairs of points on the curve with parallel tangents. The corresponding chords have an envelope with a limit point at the inflexion itself. When n = 3 we obtain a 2-parameter family of lines in R3, which may or may not have a (real) envelope. The real part of the envelope is again called the CSS of M.
    [Show full text]