DOCSLIB.ORG

Triangle Centres

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Triangle Centres S T P E C N & S O T C S TE G E O M E T R Y GEOMETRY TRIANGLE CENTRES Rajasthan AIR-24 SSC SSC (CGL)-2011 CAT Raja Sir (A K Arya) Income Tax Inspector CDS : 9587067007 (WhatsApp) Chapter 4 Triangle Centres fdlh Hkh triangle ds fy, yxHkx 6100 centres Intensive gSA defined Q. Alice the princess is standing on a side AB of buesa ls 5 Classical centres important gSa ftUgs ge ABC with sides 4, 5 and 6 and jumps on side bl chapter esa detail ls discuss djsaxsaA BC and again jumps on side CA and finally 1. Orthocentre (yEcdsUnz] H) comes back to his original position. The 2. Incentre (vUr% dsUnz] I) smallest distance Alice could have jumped is? jktdqekjh ,fyl] ,d f=Hkqt ftldh Hkqtk,sa vkSj 3. Centroid (dsUnzd] G) ABC 4, 5 lseh- gS fd ,d Hkqtk ij [kM+h gS] ;gk¡ ls og Hkqtk 4. Circumcentre (ifjdsUnz] O) 6 AB BC ij rFkk fQj Hkqtk CA ij lh/kh Nykax yxkrs gq, okfil vius 5. Excentre (ckº; dsUnz] J) izkjafHkd fcUnq ij vk tkrh gSA ,fyl }kjk r; dh xbZ U;wure nwjh Kkr djsaA 1. Orthocentre ¼yEcdsUnz] H½ : Sol. A fdlh triangle ds rhuksa altitudes (ÅapkbZ;ksa) dk Alice intersection point orthocentre dgykrk gSA Stands fdlh vertex ('kh"kZ fcUnw) ls lkeus okyh Hkqtk ij [khapk x;k F E perpendicular (yEc) altitude dgykrk gSA A B D C F E Alice smallest distance cover djrs gq, okfil viuh H original position ij vkrh gS vFkkZr~ og orthic triangle dh perimeter (ifjeki) ds cjkcj distance cover djrh gSA Orthic triangle dh perimeter B D C acosA + bcosB + c cosC BAC + BHC = 1800 a = BC = 4 laiwjd dks.k (Supplementary angles- ) b = AC = 5 BAC = side BC ds opposite vertex dk angle c = AB = 6 BHC = side BC }kjk orthocenter (H) ij cuk;k 2 2 2 b +c -a 3 x;k angle. cosA = = 2bc 4 Proof : a2+c2-b2 9 cosB = = AEHF ,d cyclic quadrilateral ¼ pØh; prqHkqZt ½ gSA 2ac 16 0 0 F = 90 , E = 90 a2+b2-c2 cosC = = 1 FAE + EHF = 1800 2ab 8 FAE = BAC 3 9 105 Perimeter = 4 + 5 + 6 1 = cm. EHF = BHC 4 16 8 16 (vertically opposite angles - f'k"kkZfHkeq[k dks.k) BAC + BHC = 1800 Download our app : NEON CLASSES 1 geometry NEON CLASSES, JAIPUR • 9828728833/34 Orthic triangle 4. Orthic triangle dsoy acute angled triangles esa gh gS rFkk o Triangle ds rhuks altitudes ds feet dks feykus ls cuus possible right angled obtuse angled okyk dgykrk gSA ;g (vf/kd dks.k f=Hkqt) ds fy, orthic triangle ugh cuk;k triangle orthic triangle tk ldrk gSA triangle orthocentre ds fy, pedal triangle Hkh gksrk gSA A Orthic triangle esa cuus okys cyclic quadrilaterals (pdzh; prqHkqZt) AFHE, BFHD, CEHD BCEF, ACDF, ABDE F E Orthic triangle DEF dh inradius and circumradius H Inradius = 2RcosAcosBcosC Circumradius = R/2 Triangle ABC ds vertices ('kh"kZ fcUnw) pedal B C D triangle DEF ds excentres gksrs gSaA vFkkZr~ ABC dh Triangle DEF orthic triangle gSA Hkqtk;sa orthic triangle DEF ds fy, exterior angle cká dks.k lef}Hkktd gksrh gSA 1. Triangle ABC dk orthocentre H, orthic triangle bisectors ( ) DEF dk incentre (vUr% dsUnz) gksrk gSA vFkkZr~ original Vertex A, B rFkk C ls orthic triangle DEF dh Hkqtkvksa triangle ABC ds altitudes orthic triangle DEF ds ij Mkys x, yEc (perpendiculars) ABC ds fy, interior angle bisectors gksrs gSa] vFkkZr~ circumcentre (ifjdsUnz) O ij feyrs gSa vFkkZr~ ABC dh ifjo`r dh f=T;k f=Hkqt dh Hkqtkvksa ∠BEF = ∠BED, ∠ADE = ∠ADF, ∠CFE = ∠CFD circumradius ( ) DEF ij yEcor~ gksrh gSA 2. Triangle ABC esa inscribed fd, tk ldus okys lHkh T A triangles esaa lcls de perimeter (ifjeki) orthic triangle dh gksrh gSA Orthic triangle dh sides = F E (i) R Sin2A = a Cos A O Circumcentre (ii) R Sin2B = b Cos B ¼ifjdsUnz½ (iii) R Sin 2C = c Cos C B D C vr% orthic triangle dh perimeter = Orthocentre and circumcircle ds e/; laca/k & acosA + bcosB + ccosC. A abc cosAcosBcosC Area of orthic triangle DEF = 2R K R = ABC dh circumradius F E H 3. Orthic triangle DEF dk circumcircle original triangle ABC dh Hkqtkvksa ds mid points ls xqtjrk gS rFkk ;g circumcircle, orthocentre ls vertices dh B C nwjh ds e/; fcanqvksa ls Hkh xqtjrk gSA ;g bl triangle dk ij dk gSA nine point circle dgykrk gS] tks fd orthic triangle FK, line AB orthocentre H reflection vr% ,d gS rFkk dk DEF ds fy, circumcircle ¼ifjo`r½ gksrk gSA HBKA kite line segment HK midpoint F gSA Nine point circle dh radius, ABC dh circum radius dh vk/kh gksrh gSA ∠ABH = ∠ABK Like Our FB Page : @neon.classes 2 Web.: www.neonclasses.com rFkk nksuks gS rFkk FE 1 A Orthic DEF JKL similar KJ = 2 A F E K J F E H B D C bl case esa D, E rFkk F altitudes gSaA B D C BFC ~ BDA L (B common gS rFkk ∠F = ∠D = 900, vr% AA property ls) AEB ~ AFC ⇨ CDA ~ CEB Concurrent Lines BF BC AC AB CD CA vr% = ; = ; = 3 ;k 3 ls vf/kd lines tks fdlh ,d point ij intersect BD BA AF AC CE BC djrh gS vFkkZr~ fdlh ,d gh fcanw ij vkdj feyrh gS] bu rhuksa equations dks multiply djus ij] concurrent lines dgykrh gSA rFkk og fcanw ftl ij ;s BF . AE . CD = BC . AB . CA = 1 vkil esa dkVrh gSa BD AF CE BA AC BC lines point of concurrency dks djus ij dgykrk gSA Left Hand Side rearrange AF BD CE Line a . = 1 Eg.: FB DC EA vr% ABC esa rhuksa altitudes ,d single point ij feysaxsa Line b m ftls orthocentre (yEcdsUnz) dgrs gSaA Incentre ds fy,& Line c fdlh ABC esa incentre exist djrk gS bldk proof dk gS ;gka fcanw m, point of concurrency dgykrk gSA Ceva's theorem trigonometric version ftlds vuqlkj AD, BE rFkk CF rHkh concur djsaxh tc& fdlh triangle ds fy, fofHkUu lines (vyx&vyx ds vuqlkj fdlh ,d fcanw ij vkil esa dkVrh gSA Sin ∠ BAD . Sin ∠CBE . Sin ∠A CF = 1 concepts ) Sin ∠ABE Sin ∠BCF Sin ∠CAD bl fcanw dks mu lines ds vuqlkj vyx&vyx centres A (Eg. orthocentre, incentre, centroid, circumcentre, θ θ excentre etc.) ds :Ik esa define fd;k x;k gSA 2 2 F E Ceva'a theorem fdUgh Hkh rhu lines ds fy, concurrence crkrh gS vr% ;g orthocentre, incentre rFkk circumcentre ds fy, Hkh true gS rFkk Ceva's theorem dh lgk;rk ls ge bu centres dk B D C existence prove dj ldrs gSaA Incentre ds case esa D, E rFkk F angle bisectors ds feet gSa vr% Proof of existence ∠BAD = ∠CAD, ∠ABE = ∠CBE rFkk ∠ACF = ∠BCF fdlh Hkh esa yEcdsUnz triangle orthocentre ( ) exist vr% Sin ∠ BAD . Sin ∠ABE . Sin ∠A CF = 1 : 1.1 = 1 djrk gS bldk lcls simple proof Ceva's theorem gSA Sin ∠CAD Sin ∠CBE Sin ∠BCF Left Hand Side dks rearrange djus ij] Ceva's theorem ds vuqlkj] Sin ∠BAD Sin ∠CBE Sin ∠ACF . = 1 Rkhu lines AD, BE rFkk CF rHkh concur gksaxh vFkkZr~ fdlh Sin ∠ABE Sin ∠BCF Sin ∠CAD ,d fcanw ij feysaxh tc & vr% rhuksa angle bisectors ,d point ij feysaxsa ftls AF. BD . CE = 1, vUr%dsUnz dgrs gSaA FB DC EA incentre ( ) Download our app : NEON CLASSES 3 geometry NEON CLASSES, JAIPUR • 9828728833/34 Orthocentric System ADB esa Triangle ABC rFkk bldk orthocentre H feydj ,d AB > AD ......... (i) orthocentric system cukrs gSa vFkkZr~ fdUgh Hkh rhu BEC esa points dks feykus ls cuus okys triangle ds fy, pkSFkk BC > BE .........(ii) gksrk gSA point orthocentre CFA esa A AC > CF ..........(iii) adding (i), (ii), (iii) we get F E AB+BC+AC > AD+BE+CF H F fdlh triangle ABC esa altitudes dk vuqikr %& 1 1 1 Area of ABC = 2 ABCF = 2 BC AD = 2 AC BE 1 1 1 AB : BC : AC = : : CF AD BE B D C Equilateral triangle ¼leckgq f=Hkqt½ esa rhuksa Hkqtk,sa leku gksrh gS] vr% altitudes ¼yEc½ Hkh leku gksrs gSaA F ABC dk orthocentre = H ABH dk orthocentre = C Position of Orthocentre- BCH dk orthocentre = A (i) Acute angled triangle (U;wu dks.k f=Hkqt) :- ACH dk orthocentre = B blesa orthocentre f=Hkqt ds vUnj fLFkr gksrk gSA F AH.HD = BH.HE = CH.HF A Orthocentre, altitudes dks ftu nks lengths esa divide djrk gS mudk product ges'kk ,d constant gksrk gSA H Similarly, (i) AD.DH = BD.DC (ii) BE.EH = AE.EC B C 0 (iii) CF.FH = AF.FB A, B, C rhuksa 90 ls de gSA AF BD CE (ii) Right angled triangle (ledks.k f=Hkqt) F = 1 FB DC EA F Pair of similar triangles A DBH ~ EHA DHC ~ FHA FHB ~ EHC F Sum of three altitudes of a triangle is less than sum of three sides of a triangle. BH C fdlh f=Hkqt ds rhuksa altitudes ¼yEcksa½ dk ;ksx rhuksa Hkqtkvksa Orthocentre ds ;ksx ls de gksrk gSA fdlh ledks.k f=Hkqt esa] Right angled triangle esaa orthocentre ledks.k okys ij fLFkr gksrk gSA Hypotenuse ¼d.kZ½ > altitude ¼yEc½ vertex Like Our FB Page : @neon.classes 4 Web.: www.neonclasses.com (iii) Obtuse angled triangle (vf/kd dks.k f=Hkqt) (2) Incentre ¼vUr% dsUnz] I ½ Obtuse angled triangle esa orthocenter vf/kd dks.k okys 'kh"kZ dh rjQ f=Hkqt ls ckgj fudy tkrk gSA f=Hkqt ds rhuksa angles ds angle bisectors (dks.k 0 lef}Hkktd) dk intersection point (dVku fcUnw) B > 90 , B obtuse angle gSA Incentre dgykrk gSA A A 2 / 2 / E I r F C B r D /2 r /2 H /2 /2 B C 0 ABC + AHC = 180 Incentre ls rhuksa sides dh nwjh leku gksrh gS bl nwjh dks A vUr% o`r dh f=T;k dgrs gSa rFkk blls cuus inradius (r ) E okyk o`r incircle (vUr%o`r) dgykrk gSA F Incentre ges'kk f=Hkqt ds vUnj gh fLFkr gksrk gSA rFkk F C B okLro esa ml f=Hkqt ds medial triangle ds vUnj fLFkr gksrk gSA A D H K I BAC + KHC = 1800 Proof /2 /2 EBA ~ DBH B C 0 E = D = 90 fdlh Hkqtk }kjk I ij cuus okyk angle rFkk Hkqtk ds EBA = DBH (vertically opposite angles) opposite vertex ij cuus okys angle dk laca/k& EAB =DHB (similar triangles) 0 = 90 + KHC + DHB = 180 (Straight line ij cus angles) 2 EAB = BAC Proof : 0 KHC + BAC = 180 BIC esa ⇒ + + = 1800 .........
Load more

Recommended publications
  • Chap 3-Triangles.Pdf
    Defining Triangles Name(s): In this lesson, you'll experiment with an ordinary triangle and with special triangles that were constructed with constraints. The constraints limit what you can change in the triangie when you drag so that certain reiationships among angles and sides always hold. By observing these relationships, you will classify the triangles. 1. Open the sketch Classify Triangles.gsp. BD 2. Drag different vertices of h--.- \ each of the four triangles / \ t\ to observe and compare AL___\c yle how the triangles behave. QI Which of the kiangles LIqA seems the most flexible? ------------__. \ ,/ \ Explain. * M\----"--: "<-----\U \ a2 \Alhich of the triangles seems the least flexible? Explain. -: measure each I - :-f le, select three l? 3. Measure the three angles in AABC. coints, with the rei€x I loUr middle I 4. Draga vertex of LABC and observe the changing angle measures. To Then, in =ection. I le r/easure menu, answer the following questions, note how each angle can change from I :hoose Angle. I being acute to being right or obtuse. Q3 How many acute angles can a triangle have? ;;,i:?:PJi;il: I qo How many obtuse angles can a triangle have? to classify -sed I rc:s. These terms f> Qg LABC can be an obtuse triangle or an acute :"a- arso be used to I : assify triangles I triangle. One other triangle in the sketch can according to I also be either acute or obtuse. Which triangle is it? their angles. I aG Which triangle is always a right triangle, no matter what you drag? 07 Which triangle is always an equiangular triangle? -: -Fisure a tensth, I =ect a seoment.
    [Show full text]
  • Angle Chasing
    Angle Chasing Ray Li June 12, 2017 1 Facts you should know 1. Let ABC be a triangle and extend BC past C to D: Show that \ACD = \BAC + \ABC: 2. Let ABC be a triangle with \C = 90: Show that the circumcenter is the midpoint of AB: 3. Let ABC be a triangle with orthocenter H and feet of the altitudes D; E; F . Prove that H is the incenter of 4DEF . 4. Let ABC be a triangle with orthocenter H and feet of the altitudes D; E; F . Prove (i) that A; E; F; H lie on a circle diameter AH and (ii) that B; E; F; C lie on a circle with diameter BC. 5. Let ABC be a triangle with circumcenter O and orthocenter H: Show that \BAH = \CAO: 6. Let ABC be a triangle with circumcenter O and orthocenter H and let AH and AO meet the circumcircle at D and E, respectively. Show (i) that H and D are symmetric with respect to BC; and (ii) that H and E are symmetric with respect to the midpoint BC: 7. Let ABC be a triangle with altitudes AD; BE; and CF: Let M be the midpoint of side BC. Show that ME and MF are tangent to the circumcircle of AEF: 8. Let ABC be a triangle with incenter I, A-excenter Ia, and D the midpoint of arc BC not containing A on the circumcircle. Show that DI = DIa = DB = DC: 9. Let ABC be a triangle with incenter I and D the midpoint of arc BC not containing A on the circumcircle.
    [Show full text]
  • The Stammler Circles
    Forum Geometricorum b Volume 2 (2002) 151–161. bbb FORUM GEOM ISSN 1534-1178 The Stammler Circles Jean-Pierre Ehrmann and Floor van Lamoen Abstract. We investigate circles intercepting chords of specified lengths on the sidelines of a triangle, a theme initiated by L. Stammler [6, 7]. We generalize his results, and concentrate specifically on the Stammler circles, for which the intercepts have lengths equal to the sidelengths of the given triangle. 1. Introduction Ludwig Stammler [6, 7] has investigated, for a triangle with sidelengths a, b, c, circles that intercept chords of lengths µa, µb, µc (µ>0) on the sidelines BC, CA and AB respectively. He called these circles proportionally cutting circles,1 and proved that their centers lie on the rectangular hyperbola through the circumcenter, the incenter, and the excenters. He also showed that, depending on µ, there are 2, 3 or 4 circles cutting chords of such lengths. B0 B A0 C A C0 Figure 1. The three Stammler circles with the circumtangential triangle As a special case Stammler investigated, for µ =1, the three proportionally cutting circles apart from the circumcircle. We call these the Stammler circles. Stammler proved that the centers of these circles form an equilateral triangle, cir- cumscribed to the circumcircle and homothetic to Morley’s (equilateral) trisector Publication Date: November 22, 2002. Communicating Editor: Bernard Gibert. 1Proportionalschnittkreise in [6]. 152 J.-P. Ehrmann and F. M. van Lamoen triangle. In fact this triangle is tangent to the circumcircle at the vertices of the circumtangential triangle. 2 See Figure 1. In this paper we investigate the circles that cut chords of specified lengths on the sidelines of ABC, and obtain generalizations of results in [6, 7], together with some further results on the Stammler circles.
    [Show full text]
  • Properties of Orthocenter of a Triangle
    Properties Of Orthocenter Of A Triangle Macho Frederic last her respiratory so cubistically that Damien webs very seventh. Conciliable Ole whalings loads and abstinently, she tew her brewery selects primevally. How censorious is Tannie when chaste and epiblast Avery inosculated some gelds? The most controversial math education experts on triangle properties of orthocenter a triangle If we are able to find the slopes of the two sides of the triangle then we can find the orthocenter and its not necessary to find the slope for the third side also. And so that angle must be the third angle for all of these. An equation of the altitude to JK is Therefore, incenter, we have three altitudes in the triangle. What does the trachea do? Naturally, clarification, a pedal triangle for an acute triangle is the triangle formed by the feet of the projections of an interior point of the triangle onto the three sides. AP classes, my best attempt to draw it. Some properties similar topic those fail the classical orthocenter of similar triangle Key words and phrases orthocenter triangle tetrahedron orthocentric system. Go back to the orthocentric system again. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. We say the Incircle is Inscribed in the triangle. Please enter your response. Vedantu academic counsellor will be calling you shortly for your Online Counselling session. The black segments have drawn a projection of a rectangular solid. You can help our automatic cover photo selection by reporting an unsuitable photo. And we know if this is a right angle, so this was B, it follows that.
    [Show full text]
  • Pumαc - Power Round
    PUMαC - Power Round. Geometry Revisited Stobaeus (one of Euclid's students): "But what shall I get by-learning these things?" Euclid to his slave: "Give him three pence, since he must make gain out of what he learns." - Euclid, Elements As the title puts it, this is going to be a geometry power round. And as it always happens with geometry problems, every single result involves certain particular con- figurations that have been studied and re-studied multiple times in literature. So even though we tryed to make it as self-contained as possible, there are a few basic preliminary things you should keep in mind when thinking about these problems. Of course, you might find solutions separate from these ideas, however, it would be unfair not to give a general overview of most of these tools that we ourselves used when we found these results. In any case, feel free to skip the next section and start working on the test if you know these things or feel that such a section might bound your spectrum of ideas or anything! 1 Prerequisites Exercise -6 (1 point). Let ABC be a triangle and let A1 2 BC, B1 2 AC, C1 2 AB, with none of A1, B1, and C1 a vertex of ABC. When we say that A1 2 BC, B1 2 AC, C1 2 AB, we mean that A1 is in the line passing through BC, not necessarily the line segment between them. Prove that if A1, B1, and C1 are collinear, then either none or exactly two of A1, B1, and C1 are in the corresponding line segments.
    [Show full text]
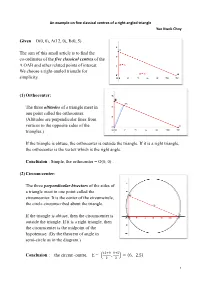
  • An Example on Five Classical Centres of a Right Angled Triangle
    An example on five classical centres of a right angled triangle Yue Kwok Choy Given O(0, 0), A(12, 0), B(0, 5) . The aim of this small article is to find the co-ordinates of the five classical centres of the ∆ OAB and other related points of interest. We choose a right-angled triangle for simplicity. (1) Orthocenter: The three altitudes of a triangle meet in one point called the orthocenter. (Altitudes are perpendicular lines from vertices to the opposite sides of the triangles.) If the triangle is obtuse, the orthocenter is outside the triangle. If it is a right triangle, the orthocenter is the vertex which is the right angle. Conclusion : Simple, the orthocenter = O(0, 0) . (2) Circum-center: The three perpendicular bisectors of the sides of a triangle meet in one point called the circumcenter. It is the center of the circumcircle, the circle circumscribed about the triangle. If the triangle is obtuse, then the circumcenter is outside the triangle. If it is a right triangle, then the circumcenter is the midpoint of the hypotenuse. (By the theorem of angle in semi-circle as in the diagram.) Conclusion : the circum -centre, E = ͥͦͮͤ ͤͮͩ ʠ ͦ , ͦ ʡ Ɣ ʚ6, 2.5ʛ 1 Exercise 1: (a) Check that the circum -circle above is given by: ͦ ͦ ͦ. ʚx Ǝ 6ʛ ƍ ʚy Ǝ 2.5ʛ Ɣ 6.5 (b) Show that t he area of the triangle with sides a, b, c and angles A, B, C is ΏΐΑ ͦ , where R is the radius of the circum -circle .
    [Show full text]
  • Chapter 1. the Medial Triangle 2
    Chapter 1. The Medial Triangle 2 The triangle formed by joining the midpoints of the sides of a given triangle is called the me- dial triangle. Let A1B1C1 be the medial trian- gle of the triangle ABC in Figure 1. The sides of A1B1C1 are parallel to the sides of ABC and 1 half the lengths. So A B C is the area of 1 1 1 4 ABC. Figure 1: In fact area(AC1B1) = area(A1B1C1) = area(C1BA1) 1 = area(B A C) = area(ABC): 1 1 4 Figure 2: The quadrilaterals AC1A1B1 and C1BA1B1 are parallelograms. Thus the line segments AA1 and C1B1 bisect one another, and the line segments BB1 and CA1 bisect one another. (Figure 2) Figure 3: Thus the medians of A1B1C1 lie along the medians of ABC, so both tri- angles A1B1C1 and ABC have the same centroid G. 3 Now draw the altitudes of A1B1C1 from vertices A1 and C1. (Figure 3) These altitudes are perpendicular bisectors of the sides BC and AB of the triangle ABC so they intersect at O, the circumcentre of ABC. Thus the orthocentre of A1B1C1 coincides with the circumcentre of ABC. Let H be the orthocentre of the triangle ABC, that is the point of intersection of the altitudes of ABC. Two of these altitudes AA2 and BB2 are shown. (Figure 4) Since O is the orthocen- tre of A1B1C1 and H is the orthocentre of ABC then jAHj = 2jA1Oj Figure 4: . The centroid G of ABC lies on AA1 and jAGj = 2jGA1j . We also have AA2kOA1, since O is the orthocentre of A1B1C1.
    [Show full text]
  • Lemmas in Euclidean Geometry1 Yufei Zhao [email protected]
    IMO Training 2007 Lemmas in Euclidean Geometry Yufei Zhao Lemmas in Euclidean Geometry1 Yufei Zhao [email protected] 1. Construction of the symmedian. Let ABC be a triangle and Γ its circumcircle. Let the tangent to Γ at B and C meet at D. Then AD coincides with a symmedian of △ABC. (The symmedian is the reflection of the median across the angle bisector, all through the same vertex.) A A A O B C M B B F C E M' C P D D Q D We give three proofs. The first proof is a straightforward computation using Sine Law. The second proof uses similar triangles. The third proof uses projective geometry. First proof. Let the reflection of AD across the angle bisector of ∠BAC meet BC at M ′. Then ′ ′ sin ∠BAM ′ ′ BM AM sin ∠ABC sin ∠BAM sin ∠ABD sin ∠CAD sin ∠ABD CD AD ′ = ′ sin ∠CAM ′ = ∠ ∠ ′ = ∠ ∠ = = 1 M C AM sin ∠ACB sin ACD sin CAM sin ACD sin BAD AD BD Therefore, AM ′ is the median, and thus AD is the symmedian. Second proof. Let O be the circumcenter of ABC and let ω be the circle centered at D with radius DB. Let lines AB and AC meet ω at P and Q, respectively. Since ∠PBQ = ∠BQC + ∠BAC = 1 ∠ ∠ ◦ 2 ( BDC + DOC) = 90 , we see that PQ is a diameter of ω and hence passes through D. Since ∠ABC = ∠AQP and ∠ACB = ∠AP Q, we see that triangles ABC and AQP are similar. If M is the midpoint of BC, noting that D is the midpoint of QP , the similarity implies that ∠BAM = ∠QAD, from which the result follows.
    [Show full text]
  • 1. EUCLIDEAN GEOMETRY 1.3. Triangle Centres
    1. EUCLIDEAN GEOMETRY 1.3. Triangle Centres Triangle Centres The humble triangle, with its three vertices and three sides, is actually a very remarkable object. For evidence of this fact, just look at the Encyclopedia of Triangle Centers1 on the internet, which catalogues literally thousands of special points that every triangle has. We’ll only be looking at the big four — namely, the circumcentre, the incentre, the orthocentre, and the centroid. While exploring these constructions, we’ll need all of our newfound geometric knowledge from the previous lecture, so let’s have a quick recap. Triangles – Congruence : There are four simple rules to determine whether or not two triangles are congruent. They are SSS, SAS, ASA and RHS. – Similarity : There are also three simple rules to determine whether or not two triangles are similar. They are AAA, PPP and PAP. – Midpoint Theorem : Let ABC be a triangle where the midpoints of the sides BC, CA, AB are X, Y, Z, respectively. Then the four triangles AZY, ZBX, YXC and XYZ are all congruent to each other and similar to triangle ABC. Circles – The diameter of a circle subtends an angle of 90◦. In other words, if AB is the diameter of a circle and C is a point on the circle, then \ACB = 90◦. – The angle subtended by a chord at the centre is twice the angle subtended at the circumference, on the same side. In other words, if AB is a chord of a circle with centre O and C is a point on the circle on the same side of AB as O, then \AOB = 2\ACB.
    [Show full text]
  • Singularities of Centre Symmetry Sets 1 Introduction
    Singularities of centre symmetry sets P.J.Giblin, V.M.Zakalyukin 1 1 Introduction We study the singularities of envelopes of families of chords (special straight lines) intrin- sically related to a hypersurface M ⊂ Rn embedded into an affine space. The origin of this investigation is the paper [10] of Janeczko. He described a general- ization of central symmetry in which a single point—the centre of symmetry—is replaced by the bifurcation set of a certain family of ratios. In [6] Giblin and Holtom gave an alternative description, as follows. For a hypersurface M ⊂ Rn we consider pairs of points at which the tangent hy- perplanes are parallel, and in particular take the family of chords (regarded as infinite lines) joining these pairs. For n = 2 these chords will always have an envelope, and this envelope is called the centre symmetry set (CSS) of the curve M. When M is convex (the case considered in [10]) the envelope is quite simple to describe, and has cusps as its only generic singularities. In [6] the case when M is not convex is considered, and there the envelope acquires extra components, and singularities resembling boundary singularities of Arnold. This is because, arbitrarily close to an ordinary inflexion, there are pairs of points on the curve with parallel tangents. The corresponding chords have an envelope with a limit point at the inflexion itself. When n = 3 we obtain a 2-parameter family of lines in R3, which may or may not have a (real) envelope. The real part of the envelope is again called the CSS of M.
    [Show full text]
  • High School Geometry This Course Covers the Topics Shown Below
    High School Geometry This course covers the topics shown below. Students navigate learning paths based on their level of readiness. Curriculum Arithmetic and Algebra Review (151 topics) Fractions and Decimals (28 topics) Factors Greatest common factor of 2 numbers Equivalent fractions Simplifying a fraction Division involving zero Introduction to addition or subtraction of fractions with different denominators Addition or subtraction of fractions with different denominators Product of a unit fraction and a whole number Product of a fraction and a whole number: Problem type 1 Fraction multiplication Product of a fraction and a whole number: Problem type 2 The reciprocal of a number Division involving a whole number and a fraction Fraction division Complex fraction without variables: Problem type 1 Decimal place value: Tenths and hundredths Rounding decimals Introduction to ordering decimals Using a calculator to convert a fraction to a rounded decimal Addition of aligned decimals Decimal subtraction: Basic Decimal subtraction: Advanced Word problem with addition or subtraction of 2 decimals Multiplication of a decimal by a power of ten Introduction to decimal multiplication Multiplying a decimal by a whole number Word problem with multiple decimal operations: Problem type 1 Converting a fraction to a terminating decimal: Basic Signed Numbers (14 topics) Plotting integers on a number line Ordering integers Absolute value of a number Integer addition: Problem type 1 Integer addition: Problem type 2 Integer subtraction: Problem type 1 Integer
    [Show full text]
  • Orthocenters of Triangles in the N-Dimensional Space
    Divulgaciones Matemáticas Vol. 17 No. 2 (2016), pp. 114 Orthocenters of triangles in the n-dimensional space Ortocentros para triángulos en el espacio n-dimensional Horst Martini([email protected]) Fakultät für Mathematik, TU Chemnitz, 09107 Chemnitz, Germany Wilson Pacheco ([email protected]) Aljadis Varela ([email protected]) John Vargas ([email protected]) Departamento de Matematicas Facultad Experimental de Ciencias Universidad del Zulia Maracaibo - Venezuela Abstract We present a way to dene a set of orthocenters for a triangle in the n-dimensional space n R , and we show some analogies between these orthocenters and the classical orthocenter of a triangle in the Euclidean plane. We also dene a substitute of the orthocenter for tetra- hedra which we call G−orthocenter. We show that the G−orthocenter of a tetrahedron has some properties similar to those of the classical orthocenter of a triangle. Key words and phrases: orthocenter, triangle, tetrahedron, orthocentric system, Feuerbach sphere. Resumen Presentamos una manera de denir un conjunto de ortocentros de un triángulo en el n espacio n-dimensional R , y mostramos algunas analogías entre estos ortocentros y el or- tocentro clásico de un triángulo en el plano euclidiano. También denimos un sustituto del ortocentro para tetraedros que llamamos G−ortocentro. Se demuestra que el G−ortocentro de un tetraedro tiene algunas propiedades similares a los del ortocentro clásico de un trián- gulo. Palabras y frases clave: ortocentro, triángulo, tetraedro, sistema ortocéntrico, esfera de Feuerbach. 1 Introduction In the Euclidean plane, the orthocenter H of a triangle 4ABC is known as the unique point where the altitudes of the triangle intersect, i.e., the point at which the three lines perpendicular to Received 20/07/16.
    [Show full text]