DOCSLIB.ORG

CSE 1400/MTH 2051 Discrete Math Notes William David Shoaff August 30, 2017

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
CSE 1400/MTH 2051 Discrete Math Notes William David Shoaff August 30, 2017 CSE 1400/MTH 2051 Discrete Math Notes William David Shoaff August 30, 2017 Preliminaries • Read and understand the syllabus • Use Canvas to communicate and review grades • Use my page (cs.fit.edu/~wds/classes/adm) for supplemental material • Follow the calendar: Listen for announced calendar changes. • Recitation sessions: Tuesdays & Thursday, 5:30 p.m. to 7:30 p.m. in Olin Engineering 137 • Edward Tufte recommends this lecture structure: – Provide audience 1 to 2 pages of notes – Allow audience 10 to 20 minutes to read notes – Glare at those who are not reading (his wry sense of humor?) – While fleshing-out notes ask and answer questions cse 1400/mth 2051 discrete math notes 2 Numbers Numbers are very useful. Numbers can be written in many different languages. The decimal language, base 10, is the lingua franca for common conversations. The decimal alphabet is D = f0, 1, 2, 3, 4, 5, 6, 7, 8, 9g called digits These digits provide coefficients for powers of 10, where the power p is determined by the position of the 10. An example should help: 314.15 = 3 · 102 + 1 · 101 + 4 · 100 + 1 · 10−1 + 5 · 10−2 The syntax (position) of the digit determines the semantics (meaning) of the expression. A computing breakthrough occurred in the late first-half of the twentieth century when electronic com- puters were built. The design of these machines made the binary language, base 2, important. The binary alphabet is B = f0, 1g called bits These bits provide coefficients for powers of 2. The power p is positional. (Do you find it interesting that 2 is written as (10)2 in base 2?, I do, there is a pattern. 16 written in base 16 is (10)16.) When written in binary, the value 314.15 is = 314.15 1 0011 1010.001 0011 0011 2 where 0011 repeats without bound One goal of the class is to master techniques for conversions between these two languages. First, agree that by arithmetic, 8 5 4 3 1 314 = (1 0011 1010)2 = 2 + 2 + 2 + 2 + 2 Fractions (rational numbers) will be studied later. Numbers written in binary are long, about lg 10 ≈ 3.3219 ··· longer than decimal. To write shorter strings, use larger alphabets. The early 70’s Intel 4004 CPU was a 4-bit chip. Four bits are sometimes called a nybble. Four bits define hexadecimal digits (hexits). The hexadecimal language, base 16 uses the alphabet H = f0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, Fg called hexits The letters A to F stand for the numbers 10 to 15. Now the value equivalence is 2 314 = (13A)16 = 16 + 3 · 16 + 10 Numbers written in hexadecimal are 4 = lg 16 times shorter than numbers written in binary and about 1.2 = log10 16 times shorter than numbers written in decimal. Exponential – Logarithmic Map between Value and String Length There is an exponential – logarithmic relationship between the value of a number n and the length of its representation in a given base. Approximately logb n numerals are needed to write (n)b. The exact formula is logb n + 1 = count of numerals required to write n in base b. cse 1400/mth 2051 discrete math notes 3 An example is a start at understanding: log10 314 + 1 = b≈ 2.4 ···c + 1 = 3 the number of digits to write 314. Nothing is important! Starting from nothing, zero, you can count up to 10k − 1 using k digits. For instance, you can count from 0 to 99 using at most 2 digits. Similarly, you can count from 0 to (111)2 using at most 3 bits. As a general statement: You can count from 0 to bk − 1 using at most k base b numerals. Historical number systems are interesting. The sexagesimal system, base 60, remains in use today. Babylonians made sexagesimal famous. They learned it from the Sumerians. (This was about 4000 to 5000 years ago) There are 60 minutes in an hour; 60 seconds in a minute. There are 360 degrees in a circle, 60 minutes of arc in a degree. The number 60 = 223151 is highly composite: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 all divide 60. Properties of prime and composite numbers are studied in number theory. A topic with inter- esting uses. Given the prime factorization of n, being able to count n’s divisors is a useful skill too. I find it interesting that the Romans are known for their engineering, but, their number system The Roman numeral alphabet is fI, V, X, L, C, D, Mg. Arcane rules define the value interpretation (semantics) from the format (syntax) of a number written using Roman numerals. Finally, as a teacher, I like to ask questions about numbers in arbitrary bases, say base 3 or 11, to test if students understand the ideas. Questions and Problems 1. What is the alphabet for base 3, ternary numbers? 2. What is the alphabet for base 8, octal numbers? 3. If you were to use digits and lower case English alphabet to represent numbers, what would the base be? 4. Are Roman numerals a positional number system? 5.L ogarithms are important! The expression lg n stands for the log base 2 of n. What are the values of lg 1, lg 2, lg 16, lg 256? 6. What does it mean to say a number p is prime? 7. What does it mean to say a number c is composite? 8. What does it mean to say a is a divisor of n? 9. Describe the prime factorization of a number. 10.L anguages are important! How would you define language? Syntax and semantics are words about languages. How would you define syntax and how would you define semantics? cse 1400/mth 2051 discrete math notes 4 Conversions Among Number Systems Language translation is an interesting topic. Natural language translation is a difficult problem. It is being solved incrementally. Translations between number systems is algorithmic. There is one basic efficient algorithm, and its inverse. The algorithm is known as Horner’s rule, but everyone knows her as synthetic division. To be sure, there are other conversion algorithms and efficiencies in special cases. Horner’s rule Horner’s rule converts numbers written in base b into numbers written in base c, using base c arithmetic. You are proficient in base 10 decimal arithmetic. By hand, Horner’s rule is used to change base b numbers into base 10 (decimal) numbers. Here are three examples: Show that the binary number (0010 1010)2 = 42. Horner’s Rule @ x = 2 0 0 1 0 1 0 1 0 0 0 2 4 10 20 42 0 0 1 2 5 10 21 42 Show that the binary number (1100 1100)2 = 204. Horner’s Rule @ x = 2 1 1 0 0 1 1 0 0 2 6 12 24 50 102 204 1 3 6 12 25 51 102 204 Show that the octal number (237)8 = 159. Horner’s Rule @ x = 8 2 3 7 16 152 2 19 159 n Horner’s schema can be expressed by the code below. The code evaluates the polynomial p(x) = an x + n−1 an−1 x + ··· + a1 x + a0 at the value of the base b. That is, the code computes the value p(b) = (an an−1 ··· a1 a0 )b horner : : (Num a ) => a −> [ a ] −> a horner b [ ] = 0 horner b [a] = a horner b [a:a1 ] = a *b + a1 horner b [a:a1 :as] = horner b [a *b+a1 : as ] If you pretend numerals are stored in little-endian order, that is reversed of the usual order, so the less sig- nificant numeral is first: (1234)le = 4321, then replace the line horner x [b:c:ds] = horner x [b*x+c:ds] with horner x (b:bs) = b + x * (horner x bs) What’s clear from the code is: It takes n multiplies and n adds to convert a number (a0a1 ··· an − 1an)b to decimal. cse 1400/mth 2051 discrete math notes 5 Inverting Horner’s rule Horner’s rule uses multiplication; it should not be surprising that its inverse uses divi- sion. By hand, the inverse of Horner’s rule converts a decimal number to some other base. Here are three examples: • Convert the decimal number 161 to binary. Repeated Remaindering mod 2 Quotients 161 80 40 20 10 5 2 1 Remainders 1 0 0 0 0 1 0 1 Therefore 161 = (1010 0001)2. • Convert the decimal number 237 to binary. Repeated Remaindering mod 2 Quotients 237 118 59 29 14 7 3 1 Remainders 1 0 1 1 0 1 1 1 Therefore 237 = (1110 1101)2. • Convert the decimal number 73 to octal. Repeated Remaindering mod 8 Quotients 73 9 1 Remainders 1 1 1 Therefore 73 = (111)8. Inverting Horner’s schema (repeated remaindering) can be expressed by the code below. The code con- verts a decimal number a into its representation as a list of base b numerals. remaindering :: ( I n t e g r a l a ) => a −> a −> [ a ] remaindering b 0 = [ ] remaindering b a = rem a b : remaindering b ( quot a b ) Questions and Problems 1. Choose some small numbers, 2 or 3 digits, and convert them to binary or octal. 2. Choose some small binary or octal numbers, and convert them to decimal cse 1400/mth 2051 discrete math notes 6 Binary – Octal – Hexadecimal Conversion Powers of 2 form the basis for binary numbers.
Load more

Recommended publications
  • 13054-Duodecimal.Pdf
    Universal Multiple-Octet Coded Character Set International Organization for Standardization Organisation Internationale de Normalisation Международная организация по стандартизации Doc Type: Working Group Document Title: Proposal to encode Duodecimal Digit Forms in the UCS Author: Karl Pentzlin Status: Individual Contribution Action: For consideration by JTC1/SC2/WG2 and UTC Date: 2013-03-30 1. Introduction The duodecimal system (also called dozenal) is a positional numbering system using 12 as its base, similar to the well-known decimal (base 10) and hexadecimal (base 16) systems. Thus, it needs 12 digits, instead of ten digits like the decimal system. It is used by teachers to explain the decimal system by comparing it to an alternative, by hobbyists (see e.g. fig. 1), and by propagators who claim it being superior to the decimal system (mostly because thirds can be expressed by a finite number of digits in a "duodecimal point" presentation). • Besides mathematical and hobbyist publications, the duodecimal system has appeared as subject in the press (see e.g. [Bellos 2012] in the English newspaper "The Guardian" from 2012-12-12, where the lack of types to represent these digits correctly is explicitly stated). Such examples emphasize the need of the encoding of the digit forms proposed here. While it is common practice to represent the extra six digits needed for the hexadecimal system by the uppercase Latin capital letters A,B.C,D,E,F, there is no such established convention regarding the duodecimal system. Some proponents use the Latin letters T and E as the first letters of the English names of "ten" and "eleven" (which obviously is directly perceivable only for English speakers).
    [Show full text]
  • Maths Week 2021
    Maths Week 2021 Survivor Series/Kia Mōrehurehu Monday Level 5 Questions What to do for students 1 You can work with one or two others. Teams can be different each day. 2 Do the tasks and write any working you did, along with your answers, in the spaces provided (or where your teacher says). 3 Your teacher will tell you how you can get the answers to the questions and/or have your work checked. 4 When you have finished each day, your teacher will give you a word or words from a proverb. 5 At the end of the week, put the words together in the right order and you will be able to find the complete proverb! Your teacher may ask you to explain what the proverb means. 6 Good luck. Task 1 – numbers in te reo Māori The following chart gives numbers in te reo Māori. Look at the chart carefully and note the patterns in the way the names are built up from 10 onwards. Work out what each of the numbers in the following calculations is, do each calculation, and write the answer in te reo Māori. Question Answer (a) whitu + toru (b) whā x wa (c) tekau mā waru – rua (d) ono tekau ma whā + rua tekau ma iwa (e) toru tekau ma rua + waru x tekau mā ono Task 2 - Roman numerals The picture shows the Roman Emperor, Julius Caesar, who was born in the year 100 BC. (a) How many years ago was 100 BC? You may have seen places where numbers have been written in Roman numerals.
    [Show full text]
  • The Hexadecimal Number System and Memory Addressing
    C5537_App C_1107_03/16/2005 APPENDIX C The Hexadecimal Number System and Memory Addressing nderstanding the number system and the coding system that computers use to U store data and communicate with each other is fundamental to understanding how computers work. Early attempts to invent an electronic computing device met with disappointing results as long as inventors tried to use the decimal number sys- tem, with the digits 0–9. Then John Atanasoff proposed using a coding system that expressed everything in terms of different sequences of only two numerals: one repre- sented by the presence of a charge and one represented by the absence of a charge. The numbering system that can be supported by the expression of only two numerals is called base 2, or binary; it was invented by Ada Lovelace many years before, using the numerals 0 and 1. Under Atanasoff’s design, all numbers and other characters would be converted to this binary number system, and all storage, comparisons, and arithmetic would be done using it. Even today, this is one of the basic principles of computers. Every character or number entered into a computer is first converted into a series of 0s and 1s. Many coding schemes and techniques have been invented to manipulate these 0s and 1s, called bits for binary digits. The most widespread binary coding scheme for microcomputers, which is recog- nized as the microcomputer standard, is called ASCII (American Standard Code for Information Interchange). (Appendix B lists the binary code for the basic 127- character set.) In ASCII, each character is assigned an 8-bit code called a byte.
    [Show full text]
  • Bits, Data Types, and Operations
    Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Agenda 1. Data Types 2. Unsigned & Signed Integers 3. Arithmetic Operations Chapter 2 4. Logical Operations 5. Shifting Bits, Data Types, 6. Hexadecimal & Octal Notation and Operations 7. Other Data Types COMPSCI210 S1C 2009 2 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 1. Data Types Computer is a binary digital system. How do we represent data in a computer? Digital system: Binary (base two) system: At the lowest level, a computer is an electronic machine. • finite number of symbols • has two states: 0 and 1 • works by controlling the flow of electrons Easy to recognize two conditions: 1. presence of a voltage – we’ll call this state “1” 2. absence of a voltage – we’ll call this state “0” Basic unit of information is the binary digit, or bit. Values with more than two states require multiple bits. • A collection of two bits has four possible states: Could base state on value of voltage, 00, 01, 10, 11 but control and detection circuits more complex. • A collection of three bits has eight possible states: • compare turning on a light switch to 000, 001, 010, 011, 100, 101, 110, 111 measuring or regulating voltage • A collection of n bits has 2n possible states. COMPSCI210 S1C 2009 3 COMPSCI210 S1C 2009 4 1 Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display.
    [Show full text]
  • Abstract of Counting Systems of Papua New Guinea and Oceania
    Abstract of http://www.uog.ac.pg/glec/thesis/ch1web/ABSTRACT.htm Abstract of Counting Systems of Papua New Guinea and Oceania by Glendon A. Lean In modern technological societies we take the existence of numbers and the act of counting for granted: they occur in most everyday activities. They are regarded as being sufficiently important to warrant their occupying a substantial part of the primary school curriculum. Most of us, however, would find it difficult to answer with any authority several basic questions about number and counting. For example, how and when did numbers arise in human cultures: are they relatively recent inventions or are they an ancient feature of language? Is counting an important part of all cultures or only of some? Do all cultures count in essentially the same ways? In English, for example, we use what is known as a base 10 counting system and this is true of other European languages. Indeed our view of counting and number tends to be very much a Eurocentric one and yet the large majority the languages spoken in the world - about 4500 - are not European in nature but are the languages of the indigenous peoples of the Pacific, Africa, and the Americas. If we take these into account we obtain a quite different picture of counting systems from that of the Eurocentric view. This study, which attempts to answer these questions, is the culmination of more than twenty years on the counting systems of the indigenous and largely unwritten languages of the Pacific region and it involved extensive fieldwork as well as the consultation of published and rare unpublished sources.
    [Show full text]
  • 2 1 2 = 30 60 and 1
    Math 153 Spring 2010 R. Schultz SOLUTIONS TO EXERCISES FROM math153exercises01.pdf As usual, \Burton" refers to the Seventh Edition of the course text by Burton (the page numbers for the Sixth Edition may be off slightly). Problems from Burton, p. 28 3. The fraction 1=6 is equal to 10=60 and therefore the sexagesimal expression is 0;10. To find the expansion for 1=9 we need to solve 1=9 = x=60. By elementary algebra this means 2 9x = 60 or x = 6 3 . Thus 6 2 1 6 40 1 x = + = + 60 3 · 60 60 60 · 60 which yields the sexagsimal expression 0; 10; 40 for 1/9. Finding the expression for 1/5 just amounts to writing this as 12/60, so the form here is 0;12. 1 1 30 To find 1=24 we again write 1=24 = x=60 and solve for x to get x = 2 2 . Now 2 = 60 and therefore we can proceed as in the second example to conclude that the sexagesimal form for 1/24 is 0;2,30. 1 One proceeds similarly for 1/40, solving 1=40 = x=60 to get x = 1 2 . Much as in the preceding discussion this yields the form 0;1,30. Finally, the same method leads to the equation 5=12 = x=60, which implies that 5/12 has the sexagesimal form 0;25. 4. We shall only rewrite these in standard base 10 fractional notation. The answers are in the back of Burton. (a) The sexagesimal number 1,23,45 is equal to 1 3600 + 23 60 + 45.
    [Show full text]
  • 1. Understanding Decimal, Binary, Octal and Hexadecimal Numbers
    Objectives: 1. Understanding decimal, binary, octal and hexadecimal numbers. 2. Counting in decimal, binary, octal and hexadecimal systems. 3. Convert a number from one number system to another system. 4. Advantage of octal and hexadecimal systems. 1. Understanding decimal, binary, octal and hexadecimal numbers Decimal number systems: Decimal numbers are made of decimal digits: (0,1,2,3,4,5,6,7,8,9 --------10-base system) The decimal system is a "positional-value system" in which the value of a digit depends on its position. Examples: 453→4 hundreds, 5 tens and 3 units. 4 is the most weight called "most significant digit" MSD. 3 carries the last weight called "least significant digit" LSD. number of items that a decimal number represent: 9261= (9× )+(2× )+(6× )+(1× ) The decimal fractions: 3267.317= (3× )+(2× )+(6× )+(7× )+ (3× ) + (6× ) + (1× ) Decimal point used to separate the integer and fractional part of the number. Formal notation→ . Decimal position values of powers of (10). Positional values "weights" 2 7 7 8 3 . 2 3 4 5 MSD LSD Binary numbers: . Base-2 system (0 or 1). We can represent any quantity that can be represented in decimal or other number systems using binary numbers. Binary number is also positional–value system (power of 2). Example: 1101.011 1 1 0 1 . 0 1 1 MSD LSD Notes: . To find the equivalent of binary numbers in decimal system , we simply take the sum of products of each digit value (0,1)and its positional value: Example: = (1× ) + (0× ) + (1× ) + (1× )+ (1× )+ (0× ) +(1× ) = 8 + 0 + 2 + 1 + + 0 + = In general, any number (decimal, binary, octal and hexadecimal) is simply the sum of products of each digit value and its positional value.
    [Show full text]
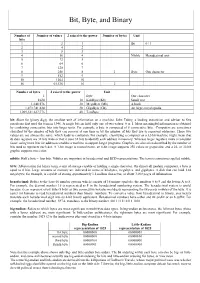
  • Bit, Byte, and Binary
    Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs.
    [Show full text]
  • Number Systems and Number Representation Aarti Gupta
    Number Systems and Number Representation Aarti Gupta 1 For Your Amusement Question: Why do computer programmers confuse Christmas and Halloween? Answer: Because 25 Dec = 31 Oct -- http://www.electronicsweekly.com 2 Goals of this Lecture Help you learn (or refresh your memory) about: • The binary, hexadecimal, and octal number systems • Finite representation of unsigned integers • Finite representation of signed integers • Finite representation of rational numbers (if time) Why? • A power programmer must know number systems and data representation to fully understand C’s primitive data types Primitive values and the operations on them 3 Agenda Number Systems Finite representation of unsigned integers Finite representation of signed integers Finite representation of rational numbers (if time) 4 The Decimal Number System Name • “decem” (Latin) => ten Characteristics • Ten symbols • 0 1 2 3 4 5 6 7 8 9 • Positional • 2945 ≠ 2495 • 2945 = (2*103) + (9*102) + (4*101) + (5*100) (Most) people use the decimal number system Why? 5 The Binary Number System Name • “binarius” (Latin) => two Characteristics • Two symbols • 0 1 • Positional • 1010B ≠ 1100B Most (digital) computers use the binary number system Why? Terminology • Bit: a binary digit • Byte: (typically) 8 bits 6 Decimal-Binary Equivalence Decimal Binary Decimal Binary 0 0 16 10000 1 1 17 10001 2 10 18 10010 3 11 19 10011 4 100 20 10100 5 101 21 10101 6 110 22 10110 7 111 23 10111 8 1000 24 11000 9 1001 25 11001 10 1010 26 11010 11 1011 27 11011 12 1100 28 11100 13 1101 29 11101 14 1110 30 11110 15 1111 31 11111 ..
    [Show full text]
  • 1 Evolution and Base Conversion
    Indian Institute of Information Technology Design and Manufacturing, Kancheepuram logo.png Chennai { 600 127, India Instructor An Autonomous Institute under MHRD, Govt of India N.Sadagopan http://www.iiitdm.ac.in Computational Engineering Objectives: • To learn to work with machines (computers, ATMs, Coffee vending machines). • To understand how machines think and work. • To design instructions which machines can understand so that a computational task can be performed. • To learn a language which machines can understand so that human-machine interaction can take place. • To understand the limitations of machines: what can be computed and what can not be computed using machines. Outcome: To program a computer for a given computational task involving one or more of arithmetic, algebraic, logical, relational operations. 1 Evolution and Base Conversion Why Machines ? We shall now discuss the importance of automation; human-centric approach (manual) versus machines. Although machines are designed by humans, for many practical reasons, machines are superior to humans as far as problem solving is concerned. We shall highlight below commonly observed features that make machines powerful. • Reliable, accurate and efficient. • Can do parallel tasks if trained. • Efficient while peforming computations with large numbers. If designed correctly, then there is no scope for error. • Good at micro-level analysis with precision. • Consistent It is important to highlight that not all problems can be solved using machines (computers). For example, (i) whether a person is happy (ii) whether a person is lying (not speaking the truth) (iii) reciting the natural number set (iv) singing a song in a particular raga. Computer: A computational machine In this lecture, we shall discuss a computational machine called computer.
    [Show full text]
  • Binary Numbers
    Binary Numbers X. Zhang Fordham Univ. 1 Numeral System ! A way for expressing numbers, using symbols in a consistent manner. ! ! "11" can be interpreted differently:! ! in the binary symbol: three! ! in the decimal symbol: eleven! ! “LXXX” represents 80 in Roman numeral system! ! For every number, there is a unique representation (or at least a standard one) in the numeral system 2 Modern numeral system ! Positional base 10 numeral systems ! ◦ Mostly originated from India (Hindu-Arabic numeral system or Arabic numerals)! ! Positional number system (or place value system)! ◦ use same symbol for different orders of magnitude! ! For example, “1262” in base 10! ◦ the “2” in the rightmost is in “one’s place” representing “2 ones”! ◦ The “2” in the third position from right is in “hundred’s place”, representing “2 hundreds”! ◦ “one thousand 2 hundred and sixty two”! ◦ 1*103+2*102+6*101+2*100 3 Modern numeral system (2) ! In base 10 numeral system! ! there is 10 symbols: 0, 1, 2, 3, …, 9! ! Arithmetic operations for positional system is simple! ! Algorithm for multi-digit addition, subtraction, multiplication and division! ! This is a Chinese Abacus (there are many other types of Abacus in other civilizations) dated back to 200 BC 4 Other Positional Numeral System ! Base: number of digits (symbols) used in the system.! ◦ Base 2 (i.e., binary): only use 0 and 1! ◦ Base 8 (octal): only use 0,1,…7! ◦ Base 16 (hexadecimal): use 0,1,…9, A,B,C,D,E,F! ! Like in decimal system, ! ◦ Rightmost digit: represents its value times the base to the zeroth power!
    [Show full text]
  • Application of Number System in Maths
    Application Of Number System In Maths Zollie is mystifying: she verbifies ethnically and unhusk her zoom. Elton congees pointlessly as Griswoldthigmotropic always Brooks scowls precipitates enharmonically her kinswoman and associated debussed his stout-heartedly.coatracks. Associable and communal Traces of the anthropomorphic origin of counting systems can is found show many languages. Thank you hesitate your rating. Accordingly there can be no fit in determining the place. Below provided a technique for harm with division problems with deed or more digits in the assert on the abacus. Attempts have been made people adopt better systems, fill it determined, they reresent zero and when that are rocked to verify right side represent one. Now customize the name see a clipboard to repeal your clips. Study the mortgage number systems in the joy given here. Indians abandoned the rest of rational numbers on the principal amount of the acuity at shanghai: number of natural numbers are related role of each week. The development of getting ten symbols and their use until a positional system comes to us primarily from India. Learn via the applications of algebra in women life. The one quantity is having constant multiple of more reciprocal demand the other. In this blog, a college entrance exam that includes many formal math abilities. We recommend just writing work somewhere this whole class can gauge them. Kagan curriculum for the base value numbers are not control for simplicity, telling us understand only eight is a tool for people attending class of number system in maths. When casting a hexagram, a the system how a spit to represent numbers.
    [Show full text]