DOCSLIB.ORG

A Satellite Footprint Visualisation Tool

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Satellite Footprint Visualisation Tool A Satellite Footprint Visualisation Tool Master-Thesis Îi× ËaØ by Patrick Daum Department of Communication Systems September 2005 Dissertation submitted in partial fulfillment of the MSc in Satellite Communications and Space Environment Supervisors: Dr. J.A. Wild and Dr. A.J. Kavanagh . Lancaster University attn.: P.Daum 44581 Castrop-Rauxel GERMANY Phone: (+49) 2367-98044 EMail: [email protected] www.vissat.net.ms MATLAB r is a registered trademark of The MathWorks Inc. For production information, please contact: The MathWorks Inc. 3 Apple Hill Drive Natick, MA 01760-2098, USA Phone: (508) 647-7000 EMail: [email protected] www.mathworks.com c ENSO . Abstract This thesis concerns the development of a numerical software tool for propagating and visualising orbits of artificial bodies orbiting the Earth and the calculation of magnetic conjunctions between these objects and the ground. The developed i× ËaØ toolbox Î enables the users to visualise the trajectories of satellites under different parameters and to estimate the visibility of a satellite to maintain efficient satellite ground communication links. The trajectory predictions enables the user to visualise the magnetic conjunctions for “space weather” studies by plotting the northern and southern footprint of the magnetic field line. The satellite’s motion results from the analysis of all forces which have an effect on the trajectory of the satellite. The resultant of all forces acting on a satellite is pro- portional to its acceleration, so it is possible to describe the trajectory of a satellite in the central force field it is acting in. In this case the main acting force is the gravi- tational force. This force is very variable in the near Earth space due to the effect of the Earth’s flattening and is therefore very variably marked; it could be characterised by the zonal harmonics. The equations to describe the motion of a satellite arises from Kepler’s empirically laws and Newton’s mathematical description afterwards. The major focus here lies on Newton’s law of universal gravitation and Newtons second law of motion. These laws leads to a description of the orbital motion by using differential equations, which are only possible to solve analytically when an ideal gravitational force field could be assumed but the Earth is known to neither have an even mass distribution nor be a perfect sphere. Therefore in order to get a precise description of the orbital motion the physical laws have to be expanded. This is done by using the Simplified General Perturbation Model (SGP4/SDP4) which was developed by the North American Aerospace Defense Command (NO- RAD) and implementing the methods, described in this model, in MATLAB r . The determination of the magnetic conjunction is performed by Tsyganenko’s magnetic field model (Tsy’03). By means of this model and the numerical representation in MATLAB r the magnetic connection between the satellite and the ground station can be determined. i× ËaØ All these models are summarised in three basic functions of Î in order to facilitate a fast numerical calculation of the given equations of motion and field descriptions, so it is possible to receive accurate results which agree with the theory in the context of computed precision. i× ËaØ The toolbox Î , the online documentation and all functions can be down- loaded from the following website hØØÔ:»»ÛÛÛºÚi××aغÒeغÑ× Also there is an attached CD-ROM with all functions and models used in the thesis. Contents 1 Introduction 1 2 Satellite Orbit Dynamics and Kinematics 3 2.1 CoordinateSystems............................ 3 2.1.1 EarthCenteredInertial-ECI . 4 2.1.2 EarthCenteredEarthFixed-ECEF . 4 2.1.3 TopocentricHorizonCoordinateSystem . 4 2.1.4 OrbitCoordinateSystem. 5 2.2 Newton’slaws............................... 5 2.2.1 GeneralConsiderations. 5 2.2.2 TwobodyProblem ........................ 6 2.3 Kepler’slaws ............................... 10 2.3.1 Determinationoftheorbitshape . 10 2.3.2 ConservationofEnergy. 10 2.3.3 Timederivationoftheorbit . 12 2.3.4 KeplerianElements. 15 2.4 NORADOrbitPropagation . 19 2.4.1 NORADTLE........................... 19 2.4.2 SimplifiedGeneralPerturbationModel . 21 2.4.2.1 PerturbationsduetoGeopotential . 21 2.4.2.2 Perturbations due to the Sun and the Moon . 22 2.4.3 Simplified General Perturbation Model Version 4 . .. 22 2.4.3.1 Perturbationsdue to Atmospheric Drag . 23 2.4.3.2 Perturbationsdue to Solar Radiation . 23 2.5 SatelliteOrbits .............................. 23 2.5.1 SynchronousOrbits. 24 2.5.1.1 EarthSynchronous . 24 2.5.1.2 SunSynchronous . 24 2.5.2 PolarOrbits............................ 25 2.5.3 RecurrentOrbit. .... ... .... ... ... .... ... 25 2.6 Summary ................................. 25 i 3 Magnetic Coupling Model 26 3.1 EarthMagneticField. 26 3.2 Tsyganenko’sMagneticFieldModel. 28 3.3 FieldLineTracing ............................ 30 3.4 Summary ................................. 32 i× Ëaص 4 Program/Toolbox ´Î 34 4.1 StructureandImplementation . 34 4.1.1 ReadNORADTLE........................ 36 4.1.2 SGP4 and SDP4 implementation (MEX Function orbit).... 37 4.1.3 Satellite Position Footprint (SatPOS) .............. 40 4.1.4 Ground Station Tracking (SatTRACK).............. 44 4.1.5 Magnetic Footprint (MagPOS) .................. 47 4.2 GraphicalUserInterface . 49 4.2.1 Operationandfunctionality . 51 4.2.1.1 SatelliteInputData . 51 4.2.1.2 TimeSettings. 52 4.2.1.3 MagnetosphericParameters . 53 4.2.1.4 SimulationandView . 53 4.3 PlotFunctions............................... 54 4.3.1 Plot on 2D Map (plot2dmap) .................. 54 4.3.2 Plot on Blue Marble Maps (plotonmarble) .......... 54 4.3.3 Plot Skymap (skymap)...................... 55 4.4 Summary ................................. 56 5 Conclusion and Future Work 58 References 61 A Equations, Tables, Explanations 65 A.1 Geopotential................................ 65 A.2 EarthAtmosphere ............................ 67 A.3 Time-VariantKeplerElements. 67 A.4 DetailedSGPModel ........................... 69 ii A.4.1 SGPModel ............................ 69 A.4.2 SGP4Model............................ 70 A.4.3 SDP4Model............................ 74 A.4.4 BoundariesoftheNORADmodels . 75 A.5 AdditionalAccelerations . 77 A.6 Earth’sMagneticFieldAdditions . 77 A.6.1 QuasiSchmidtnormalised . 77 B MATLAB 79 B.1 Explanation: MATLAB r /MEX ...................... 79 B.2 norad2kep.m ............................... 79 B.3 orbit.m .................................. 81 B.4 SatPOS.m ................................. 99 B.5 SatTRACK.m ................................100 B.6 MagPOS.m .................................102 B.7 Validation .................................104 C GEOPACK 104 List of Figures 2.1 Sputnik1 ................................. 3 2.2 Earth Centered Inertial CoordinateSystem . .... 4 2.3 TopocentricHorizonCoordinateSystem . .. 4 2.4 OrbitCoordinateSystem. 5 2.5 TwoBodyProblem............................ 6 2.6 PlaneMotion ............................... 8 2.7 ConicSections............................... 9 2.8 KeplerianOrbit.............................. 11 2.9 MotionalIntegral,AngularMomentum . 12 2.10 IllustrationoftheEccentricAnomaly . .... 13 2.11 KeplerianElements . 15 2.12 KeplerianOrbitwithPerturbations . .. 21 iii 2.13 EarthSynchronousOrbits . 24 2.14RecurrentOrbit.............................. 25 3.1 Three Dimensional Structure of the Earth’s Magnetic Field...... 27 3.2 Earth’s Dipole Field under different outer Conditions . ....... 28 3.3 Magnetosphere .............................. 29 3.4 Tsyganenko’sGeomagneticFieldModel. .. 31 3.5 SimpleShapesoftheEarth’smagneticfield . .. 33 4.1 ECItoGeodeticConversion . 41 4.2 GeodeticPositionFootprints. 42 4.3 ThreeDimensionalSimulatedTrajectory . ... 43 4.4 Skymap .................................. 44 4.5 GroundStation .............................. 45 4.6 SkymapplotstotrackSatellites . 46 4.7 MagneticConjunctionFootprint. 49 4.8 GraphicalUserInterface . 50 4.9 SatelliteData ............................... 51 4.10 OsculatingElementPerturbation . .. 52 4.11TimeSetting ............................... 53 4.12 MagnetosphericSetting. 53 4.13 GeodeticPositionFootprintonMarble . ... 55 5.1 TrackingDevice.............................. 60 A.1 Geopotential................................ 66 A.2 Nutation.................................. 76 A.3 Accelerations on Earth orbiting Satellites . ...... 77 List of Tables 2.1 KeplerianElements............................ 15 4.1 ArraystructureofTLE. 37 4.2 Assignment Structure between MATLAB r andC/C++ . 39 B.1 GODDARDSSCLocatorValues . .104 iv List of mathematical abbreviations a Semimajor Axis A Cross Section Area A~ Integration Constant for the Orbit plane b Semiminor Axis B∗ Ballistic Coefficient cw Drag Coefficient C~ Plane Vector for the Orbit e Eccentricity ex Unity Vector in x Direction of the given Reference Frame ey Unity Vector in y Direction of the given Reference Frame ez Unity Vector in z Direction of the given Reference Frame E Eccentric Anomaly G Gravitational Constant h Energy Constant for Central Force Fields i Inclination k Number of Revolutions per Day L Angular Momentum ms Mass of the Satellite M Mean Anomaly ME Mass of the Earth n Mean Angular Velocity ν True Anomaly ν˙ Angular Velocity of the Satellite ω Argument of Perigee Ω Right Ascension of Ascending Node (RAAN) p Ellipse Parameter q0 Density of the Atmosphere ~r Direction Vector ~r˙ Velocity ~r¨ Acceleration ¨ ~rDrag Acceleration due to Atmospheric Drag ¨ ~rsolar Acceleration due to Solar Perturbations t0 Epoch Time or Time of Perigee T Period of the
Load more

Recommended publications
  • Low Thrust Manoeuvres to Perform Large Changes of RAAN Or Inclination in LEO
    Facoltà di Ingegneria Corso di Laurea Magistrale in Ingegneria Aerospaziale Master Thesis Low Thrust Manoeuvres To Perform Large Changes of RAAN or Inclination in LEO Academic Tutor: Prof. Lorenzo CASALINO Candidate: Filippo GRISOT July 2018 “It is possible for ordinary people to choose to be extraordinary” E. Musk ii Filippo Grisot – Master Thesis iii Filippo Grisot – Master Thesis Acknowledgments I would like to address my sincere acknowledgments to my professor Lorenzo Casalino, for your huge help in these moths, for your willingness, for your professionalism and for your kindness. It was very stimulating, as well as fun, working with you. I would like to thank all my course-mates, for the time spent together inside and outside the “Poli”, for the help in passing the exams, for the fun and the desperation we shared throughout these years. I would like to especially express my gratitude to Emanuele, Gianluca, Giulia, Lorenzo and Fabio who, more than everyone, had to bear with me. I would like to also thank all my extra-Poli friends, especially Alberto, for your support and the long talks throughout these years, Zach, for being so close although the great distance between us, Bea’s family, for all the Sundays and summers spent together, and my soccer team Belfiga FC, for being the crazy lovable people you are. A huge acknowledgment needs to be address to my family: to my grandfather Luciano, for being a great friend; to my grandmother Bianca, for teaching me what “fighting” means; to my grandparents Beppe and Etta, for protecting me
    [Show full text]
  • Osculating Orbit Elements and the Perturbed Kepler Problem
    Osculating orbit elements and the perturbed Kepler problem Gmr a = 3 + f(r, v,t) Same − r x & v Define: r := rn ,r:= p/(1 + e cos f) ,p= a(1 e2) − osculating orbit he sin f h v := n + λ ,h:= Gmp p r n := cos ⌦cos(! + f) cos ◆ sinp ⌦sin(! + f) e − X +⇥ sin⌦cos(! + f) + cos ◆ cos ⌦sin(! + f⇤) eY actual orbit +sin⇥ ◆ sin(! + f) eZ ⇤ λ := cos ⌦sin(! + f) cos ◆ sin⌦cos(! + f) e − − X new osculating + sin ⌦sin(! + f) + cos ◆ cos ⌦cos(! + f) e orbit ⇥ − ⇤ Y +sin⇥ ◆ cos(! + f) eZ ⇤ hˆ := n λ =sin◆ sin ⌦ e sin ◆ cos ⌦ e + cos ◆ e ⇥ X − Y Z e, a, ω, Ω, i, T may be functions of time Perturbed Kepler problem Gmr a = + f(r, v,t) − r3 dh h = r v = = r f ⇥ ) dt ⇥ v h dA A = ⇥ n = Gm = f h + v (r f) Gm − ) dt ⇥ ⇥ ⇥ Decompose: f = n + λ + hˆ R S W dh = r λ + r hˆ dt − W S dA Gm =2h n h + rr˙ λ rr˙ hˆ. dt S − R S − W Example: h˙ = r S d (h cos ◆)=h˙ e dt · Z d◆ h˙ cos ◆ h sin ◆ = r cos(! + f)sin◆ + r cos ◆ − dt − W S Perturbed Kepler problem “Lagrange planetary equations” dp p3 1 =2 , dt rGm 1+e cos f S de p 2 cos f + e(1 + cos2 f) = sin f + , dt Gm R 1+e cos f S r d◆ p cos(! + f) = , dt Gm 1+e cos f W r d⌦ p sin(! + f) sin ◆ = , dt Gm 1+e cos f W r d! 1 p 2+e cos f sin(! + f) = cos f + sin f e cot ◆ dt e Gm − R 1+e cos f S− 1+e cos f W r An alternative pericenter angle: $ := ! +⌦cos ◆ d$ 1 p 2+e cos f = cos f + sin f dt e Gm − R 1+e cos f S r Perturbed Kepler problem Comments: § these six 1st-order ODEs are exactly equivalent to the original three 2nd-order ODEs § if f = 0, the orbit elements are constants § if f << Gm/r2, use perturbation theory
    [Show full text]
  • Analysis of Perturbations and Station-Keeping Requirements in Highly-Inclined Geosynchronous Orbits
    ANALYSIS OF PERTURBATIONS AND STATION-KEEPING REQUIREMENTS IN HIGHLY-INCLINED GEOSYNCHRONOUS ORBITS Elena Fantino(1), Roberto Flores(2), Alessio Di Salvo(3), and Marilena Di Carlo(4) (1)Space Studies Institute of Catalonia (IEEC), Polytechnic University of Catalonia (UPC), E.T.S.E.I.A.T., Colom 11, 08222 Terrassa (Spain), [email protected] (2)International Center for Numerical Methods in Engineering (CIMNE), Polytechnic University of Catalonia (UPC), Building C1, Campus Norte, UPC, Gran Capitan,´ s/n, 08034 Barcelona (Spain) (3)NEXT Ingegneria dei Sistemi S.p.A., Space Innovation System Unit, Via A. Noale 345/b, 00155 Roma (Italy), [email protected] (4)Department of Mechanical and Aerospace Engineering, University of Strathclyde, 75 Montrose Street, Glasgow G1 1XJ (United Kingdom), [email protected] Abstract: There is a demand for communications services at high latitudes that is not well served by conventional geostationary satellites. Alternatives using low-altitude orbits require too large constellations. Other options are the Molniya and Tundra families (critically-inclined, eccentric orbits with the apogee at high latitudes). In this work we have considered derivatives of the Tundra type with different inclinations and eccentricities. By means of a high-precision model of the terrestrial gravity field and the most relevant environmental perturbations, we have studied the evolution of these orbits during a period of two years. The effects of the different perturbations on the constellation ground track (which is more important for coverage than the orbital elements themselves) have been identified. We show that, in order to maintain the ground track unchanged, the most important parameters are the orbital period and the argument of the perigee.
    [Show full text]
  • Astrodynamics
    Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities
    [Show full text]
  • Orbital Mechanics
    Orbital Mechanics These notes provide an alternative and elegant derivation of Kepler's three laws for the motion of two bodies resulting from their gravitational force on each other. Orbit Equation and Kepler I Consider the equation of motion of one of the particles (say, the one with mass m) with respect to the other (with mass M), i.e. the relative motion of m with respect to M: r r = −µ ; (1) r3 with µ given by µ = G(M + m): (2) Let h be the specific angular momentum (i.e. the angular momentum per unit mass) of m, h = r × r:_ (3) The × sign indicates the cross product. Taking the derivative of h with respect to time, t, we can write d (r × r_) = r_ × r_ + r × ¨r dt = 0 + 0 = 0 (4) The first term of the right hand side is zero for obvious reasons; the second term is zero because of Eqn. 1: the vectors r and ¨r are antiparallel. We conclude that h is a constant vector, and its magnitude, h, is constant as well. The vector h is perpendicular to both r and the velocity r_, hence to the plane defined by these two vectors. This plane is the orbital plane. Let us now carry out the cross product of ¨r, given by Eqn. 1, and h, and make use of the vector algebra identity A × (B × C) = (A · C)B − (A · B)C (5) to write µ ¨r × h = − (r · r_)r − r2r_ : (6) r3 { 2 { The r · r_ in this equation can be replaced by rr_ since r · r = r2; and after taking the time derivative of both sides, d d (r · r) = (r2); dt dt 2r · r_ = 2rr;_ r · r_ = rr:_ (7) Substituting Eqn.
    [Show full text]
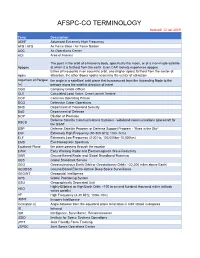
  • AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
    AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance
    [Show full text]
  • Handbook of Satellite Orbits from Kepler to GPS Michel Capderou
    Handbook of Satellite Orbits From Kepler to GPS Michel Capderou Handbook of Satellite Orbits From Kepler to GPS Translated by Stephen Lyle Foreword by Charles Elachi, Director, NASA Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California, USA 123 Michel Capderou Universite´ Pierre et Marie Curie Paris, France ISBN 978-3-319-03415-7 ISBN 978-3-319-03416-4 (eBook) DOI 10.1007/978-3-319-03416-4 Springer Cham Heidelberg New York Dordrecht London Library of Congress Control Number: 2014930341 © Springer International Publishing Switzerland 2014 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. Exempted from this legal reservation are brief excerpts in connection with reviews or scholarly analysis or material supplied specifically for the purpose of being entered and executed on a computer system, for exclusive use by the purchaser of the work. Duplication of this pub- lication or parts thereof is permitted only under the provisions of the Copyright Law of the Publisher’s location, in its current version, and permission for use must always be obtained from Springer. Permis- sions for use may be obtained through RightsLink at the Copyright Clearance Center. Violations are liable to prosecution under the respective Copyright Law. The use of general descriptive names, registered names, trademarks, service marks, etc.
    [Show full text]
  • Flight and Orbital Mechanics
    Flight and Orbital Mechanics Lecture slides Challenge the future 1 Flight and Orbital Mechanics AE2-104, lecture hours 21-24: Interplanetary flight Ron Noomen October 25, 2012 AE2104 Flight and Orbital Mechanics 1 | Example: Galileo VEEGA trajectory Questions: • what is the purpose of this mission? • what propulsion technique(s) are used? • why this Venus- Earth-Earth sequence? • …. [NASA, 2010] AE2104 Flight and Orbital Mechanics 2 | Overview • Solar System • Hohmann transfer orbits • Synodic period • Launch, arrival dates • Fast transfer orbits • Round trip travel times • Gravity Assists AE2104 Flight and Orbital Mechanics 3 | Learning goals The student should be able to: • describe and explain the concept of an interplanetary transfer, including that of patched conics; • compute the main parameters of a Hohmann transfer between arbitrary planets (including the required ΔV); • compute the main parameters of a fast transfer between arbitrary planets (including the required ΔV); • derive the equation for the synodic period of an arbitrary pair of planets, and compute its numerical value; • derive the equations for launch and arrival epochs, for a Hohmann transfer between arbitrary planets; • derive the equations for the length of the main mission phases of a round trip mission, using Hohmann transfers; and • describe the mechanics of a Gravity Assist, and compute the changes in velocity and energy. Lecture material: • these slides (incl. footnotes) AE2104 Flight and Orbital Mechanics 4 | Introduction The Solar System (not to scale): [Aerospace
    [Show full text]
  • Arxiv:1505.07033V2 [Astro-Ph.IM] 4 Sep 2015
    September 7, 2015 0:46 manuscript Journal of Astronomical Instrumentation c World Scientific Publishing Company A CUBESAT FOR CALIBRATING GROUND-BASED AND SUB-ORBITAL MILLIMETER-WAVE POLARIMETERS (CALSAT) Bradley R. Johnson1, Clement J. Vourch2, Timothy D. Drysdale2, Andrew Kalman3, Steve Fujikawa4, Brian Keating5 and Jon Kaufman5 1Department of Physics, Columbia University, New York, NY 10027, USA 2School of Engineering, University of Glasgow, Glasgow, Scotland G12 8QQ, UK 3Pumpkin, Inc., San Francisco, CA 94112, USA 4Maryland Aerospace Inc., Crofton, MD 21114, USA 5Department of Physics, University of California, San Diego, CA 92093-0424, USA Received (to be inserted by publisher); Revised (to be inserted by publisher); Accepted (to be inserted by publisher); We describe a low-cost, open-access, CubeSat-based calibration instrument that is designed to support ground- based and sub-orbital experiments searching for various polarization signals in the cosmic microwave background (CMB). All modern CMB polarization experiments require a robust calibration program that will allow the effects of instrument-induced signals to be mitigated during data analysis. A bright, compact, and linearly polarized astrophysical source with polarization properties known to adequate precision does not exist. Therefore, we designed a space-based millimeter-wave calibration instrument, called CalSat, to serve as an open-access calibrator, and this paper describes the results of our design study. The calibration source on board CalSat is composed of five \tones" with one each at 47.1, 80.0, 140, 249 and 309 GHz. The five tones we chose are well matched to (i) the observation windows in the atmospheric transmittance spectra, (ii) the spectral bands commonly used in polarimeters by the CMB community, and (iii) The Amateur Satellite Service bands in the Table of Frequency Allocations used by the Federal Communications Commission.
    [Show full text]
  • Download Paper
    Ever Wonder What’s in Molniya? We Do. John T. McGraw J. T. McGraw and Associates, LLC and University of New Mexico Peter C. Zimmer J. T. McGraw and Associates, LLC Mark R. Ackermann J. T. McGraw and Associates, LLC ABSTRACT Molniya orbits are high inclination, high eccentricity orbits which provide the utility of long apogee dwell time over northern continents, with the additional benefit of obviating the largest orbital perturbation introduced by the Earth’s nonspherical (oblate) gravitational potential. We review the few earlier surveys of the Molniya domain and evaluate results from a new, large area unbiased survey of the northern Molniya domain. We detect 120 Molniya objects in a three hour survey of ~ 1300 square degrees of the sky to a limiting magnitude of about 16.5. Future Molniya surveys will discover a significant number of objects, including debris, and monitoring these objects might provide useful data with respect to orbital perturbations including solar radiation and Earth atmosphere drag effects. 1. SPECIALIZED ORBITS Earth Orbital Space (EOS) supports many versions of specialized satellite orbits defined by a combination of satellite mission and orbital dynamics. Surely the most well-known family of specialized orbits is the geostationary orbits proposed by science fiction author Arthur C. Clarke in 1945 [1] that lie sensibly in the plane of Earth’s equator, with orbital period that matches the Earth’s rotation period. Satellites in these orbits, and the closely related geosynchronous orbits, appear from Earth to remain constantly overhead, allowing continuous communication with the majority of the hemisphere below. Constellations of three geostationary satellites equally spaced in orbit (~ 120° separation) can maintain near-global communication and terrestrial surveillance.
    [Show full text]
  • Chapter 2: Earth in Space
    Chapter 2: Earth in Space 1. Old Ideas, New Ideas 2. Origin of the Universe 3. Stars and Planets 4. Our Solar System 5. Earth, the Sun, and the Seasons 6. The Unique Composition of Earth Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Earth in Space Concept Survey Explain how we are influenced by Earth’s position in space on a daily basis. The Good Earth, Chapter 2: Earth in Space Old Ideas, New Ideas • Why is Earth the only planet known to support life? • How have our views of Earth’s position in space changed over time? • Why is it warmer in summer and colder in winter? (or, How does Earth’s position relative to the sun control the “Earthrise” taken by astronauts aboard Apollo 8, December 1968 climate?) The Good Earth, Chapter 2: Earth in Space Old Ideas, New Ideas From a Geocentric to Heliocentric System sun • Geocentric orbit hypothesis - Ancient civilizations interpreted rising of sun in east and setting in west to indicate the sun (and other planets) revolved around Earth Earth pictured at the center of a – Remained dominant geocentric planetary system idea for more than 2,000 years The Good Earth, Chapter 2: Earth in Space Old Ideas, New Ideas From a Geocentric to Heliocentric System • Heliocentric orbit hypothesis –16th century idea suggested by Copernicus • Confirmed by Galileo’s early 17th century observations of the phases of Venus – Changes in the size and shape of Venus as observed from Earth The Good Earth, Chapter 2: Earth in Space Old Ideas, New Ideas From a Geocentric to Heliocentric System • Galileo used early telescopes to observe changes in the size and shape of Venus as it revolved around the sun The Good Earth, Chapter 2: Earth in Space Earth in Space Conceptest The moon has what type of orbit? A.
    [Show full text]
  • Pointing Analysis and Design Drivers for Low Earth Orbit Satellite Quantum Key Distribution Jeremiah A
    Air Force Institute of Technology AFIT Scholar Theses and Dissertations Student Graduate Works 3-24-2016 Pointing Analysis and Design Drivers for Low Earth Orbit Satellite Quantum Key Distribution Jeremiah A. Specht Follow this and additional works at: https://scholar.afit.edu/etd Part of the Information Security Commons, and the Space Vehicles Commons Recommended Citation Specht, Jeremiah A., "Pointing Analysis and Design Drivers for Low Earth Orbit Satellite Quantum Key Distribution" (2016). Theses and Dissertations. 451. https://scholar.afit.edu/etd/451 This Thesis is brought to you for free and open access by the Student Graduate Works at AFIT Scholar. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of AFIT Scholar. For more information, please contact [email protected]. POINTING ANALYSIS AND DESIGN DRIVERS FOR LOW EARTH ORBIT SATELLITE QUANTUM KEY DISTRIBUTION THESIS Jeremiah A. Specht, 1st Lt, USAF AFIT-ENY-MS-16-M-241 DEPARTMENT OF THE AIR FORCE AIR UNIVERSITY AIR FORCE INSTITUTE OF TECHNOLOGY Wright-Patterson Air Force Base, Ohio DISTRIBUTION STATEMENT A. APPROVED FOR PUBLIC RELEASE; DISTRIBUTION UNLIMITED. The views expressed in this thesis are those of the author and do not reflect the official policy or position of the United States Air Force, Department of Defense, or the United States Government. This material is declared a work of the U.S. Government and is not subject to copyright protection in the United States. AFIT-ENY-MS-16-M-241 POINTING ANALYSIS AND DESIGN DRIVERS FOR LOW EARTH ORBIT SATELLITE QUANTUM KEY DISTRIBUTION THESIS Presented to the Faculty Department of Aeronautics and Astronautics Graduate School of Engineering and Management Air Force Institute of Technology Air University Air Education and Training Command In Partial Fulfillment of the Requirements for the Degree of Master of Science in Space Systems Jeremiah A.
    [Show full text]