Using Future Treatments to Detect and Reduce Hidden Bias
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Standardized Regression Coefficients and Newly Proposed Estimators for R2 in Multiply Imputed Data
psychometrika—vol. 85, no. 1, 185–205 March 2020 https://doi.org/10.1007/s11336-020-09696-4 STANDARDIZED REGRESSION COEFFICIENTS AND NEWLY PROPOSED ESTIMATORS FOR R2 IN MULTIPLY IMPUTED DATA Joost R. van Ginkel LEIDEN UNIVERSITY Whenever statistical analyses are applied to multiply imputed datasets, specific formulas are needed to combine the results into one overall analysis, also called combination rules. In the context of regression analysis, combination rules for the unstandardized regression coefficients, the t-tests of the regression coefficients, and the F-tests for testing R2 for significance have long been established. However, there is still no general agreement on how to combine the point estimators of R2 in multiple regression applied to multiply imputed datasets. Additionally, no combination rules for standardized regression coefficients and their confidence intervals seem to have been developed at all. In the current article, two sets of combination rules for the standardized regression coefficients and their confidence intervals are proposed, and their statistical properties are discussed. Additionally, two improved point estimators of R2 in multiply imputed data are proposed, which in their computation use the pooled standardized regression coefficients. Simulations show that the proposed pooled standardized coefficients produce only small bias and that their 95% confidence intervals produce coverage close to the theoretical 95%. Furthermore, the simulations show that the newly proposed pooled estimates for R2 are less biased than two earlier proposed pooled estimates. Key words: missing data, multiple imputation, coefficient of determination, standardized coefficient, regression analysis. 1. Introduction Multiple imputation (Rubin 1987) is a widely recommended procedure to deal with missing data. -

Prediction of Exercise Behavior Using the Exercise and Self-Esteem Model" (1995)
University of Rhode Island DigitalCommons@URI Open Access Master's Theses 1995 Prediction of Exercise Behavior Using the Exercise and Self- Esteem Model Gerard Moreau University of Rhode Island Follow this and additional works at: https://digitalcommons.uri.edu/theses Recommended Citation Moreau, Gerard, "Prediction of Exercise Behavior Using the Exercise and Self-Esteem Model" (1995). Open Access Master's Theses. Paper 1584. https://digitalcommons.uri.edu/theses/1584 This Thesis is brought to you for free and open access by DigitalCommons@URI. It has been accepted for inclusion in Open Access Master's Theses by an authorized administrator of DigitalCommons@URI. For more information, please contact [email protected]. PREDICTION OF EXERCISE BEHAVIOR USING THE EXERCISE AND SELF-ESTEEM MODEL BY GERARD MOREAU A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE IN PHYSICAL EDUCATION UNIVERSITY OF RHODE ISLAND 1995 Abstract The intent of this study was to compare the capability of self-efficacies and self-concept of physical ability to predict weight training and jogging behavior. The study consisted of 295 college students ( 123 males and 172 females), from the University of Rhode Island. The subjects received a battery of psychological tests consisting of the Physical Self-Perception Profile (PSPP), the Perceived Importance Profile (PIP), the General Self-Worth Scale (GSW), three self-efficacy scales, assessing jogging , weight training, and hard intensive studying, and a survey of recreational activities that recorded the number of sessions per week and number of minutes per session of each recreational activity the subject participated in. -

Download the Answers
ANSWERS TO EXERCISES AND REVIEW QUESTIONS PART FOUR: STATISTICAL TECHNIQUES TO EXPLORE RELATIONSHIPS AMONG VARIABLES You should review the material in the introduction to Part Four and in Chapters 11, 12, 13, 14 and 15 of the SPSS Survival Manual before attempting these exercises. Correlation 4.1 Using the data file survey.sav follow the instructions in Chapter 11 to explore the relationship between the total mastery scale (measuring control) and life satisfaction (tlifesat). Present the results in a brief report. Correlations tlifesat total tmast total life satisfaction mastery tlifesat total life satisfaction Pearson Correlation 1 .444** Sig. (2-tailed) .000 N 436 436 tmast total mastery Pearson Correlation .444** 1 Sig. (2-tailed) .000 N 436 436 **. Correlation is significant at the 0.01 level (2-tailed). The relationship between mastery and life satisfaction was explored using Pearson’s product moment correlation. There was a moderate positive correlation (r=.44, p<.0001) suggesting that people who felt they had control over their lives had higher levels of life satisfaction. 4.2 Use the instructions in Chapter 11 to generate a full correlation matrix to check the intercorrelations among the following variables. (a) age (b) perceived stress (tpstress) (c) positive affect (tposaff) (d) negative affect (tnegaff) (e) life satisfaction (tlifesat) 1 Correlations tpstress total tposaff total tnegaff total tlifesat total age perceived stress positive affect negative affect life satisfaction age Pearson Correlation 1 -.127** .069 -.171** .059 Sig. (2-tailed) .008 .150 .000 .222 N 439 433 436 435 436 tpstress total Pearson Correlation -.127** 1 -.442** .674** -.494** perceived stress Sig. -
Linear Regression and Correlation
NCSS Statistical Software NCSS.com Chapter 300 Linear Regression and Correlation Introduction Linear Regression refers to a group of techniques for fitting and studying the straight-line relationship between two variables. Linear regression estimates the regression coefficients β0 and β1 in the equation Yj = β0 + β1 X j + ε j where X is the independent variable, Y is the dependent variable, β0 is the Y intercept, β1 is the slope, and ε is the error. In order to calculate confidence intervals and hypothesis tests, it is assumed that the errors are independent and normally distributed with mean zero and variance σ 2 . Given a sample of N observations on X and Y, the method of least squares estimates β0 and β1 as well as various other quantities that describe the precision of the estimates and the goodness-of-fit of the straight line to the data. Since the estimated line will seldom fit the data exactly, a term for the discrepancy between the actual and fitted data values must be added. The equation then becomes y j = b0 + b1x j + e j = y j + e j 300-1 © NCSS, LLC. All Rights Reserved. NCSS Statistical Software NCSS.com Linear Regression and Correlation where j is the observation (row) number, b0 estimates β0 , b1 estimates β1 , and e j is the discrepancy between the actual data value y j and the fitted value given by the regression equation, which is often referred to as y j . This discrepancy is usually referred to as the residual. Note that the linear regression equation is a mathematical model describing the relationship between X and Y. -

2. Linear Models for Continuous Data
Chapter 2 Linear Models for Continuous Data The starting point in our exploration of statistical models in social research will be the classical linear model. Stops along the way include multiple linear regression, analysis of variance, and analysis of covariance. We will also discuss regression diagnostics and remedies. 2.1 Introduction to Linear Models Linear models are used to study how a quantitative variable depends on one or more predictors or explanatory variables. The predictors themselves may be quantitative or qualitative. 2.1.1 The Program Effort Data We will illustrate the use of linear models for continuous data using a small dataset extracted from Mauldin and Berelson (1978) and reproduced in Table 2.1. The data include an index of social setting, an index of family planning effort, and the percent decline in the crude birth rate (CBR)|the number of births per thousand population|between 1965 and 1975, for 20 countries in Latin America and the Caribbean. The index of social setting combines seven social indicators, namely lit- eracy, school enrollment, life expectancy, infant mortality, percent of males aged 15{64 in the non-agricultural labor force, gross national product per capita and percent of population living in urban areas. Higher scores repre- sent higher socio-economic levels. G. Rodr´ıguez. Revised September 2007 2 CHAPTER 2. LINEAR MODELS FOR CONTINUOUS DATA Table 2.1: The Program Effort Data Setting Effort CBR Decline Bolivia 46 0 1 Brazil 74 0 10 Chile 89 16 29 Colombia 77 16 25 CostaRica 84 21 29 Cuba 89 15 40 Dominican Rep 68 14 21 Ecuador 70 6 0 El Salvador 60 13 13 Guatemala 55 9 4 Haiti 35 3 0 Honduras 51 7 7 Jamaica 87 23 21 Mexico 83 4 9 Nicaragua 68 0 7 Panama 84 19 22 Paraguay 74 3 6 Peru 73 0 2 Trinidad-Tobago 84 15 29 Venezuela 91 7 11 The index of family planning effort combines 15 different program indi- cators, including such aspects as the existence of an official family planning policy, the availability of contraceptive methods, and the structure of the family planning program. -

Regression Analysis 1
SPSS PC Version 10: Regression Analysis 1 The following uses a set of variables from the “1995 National Survey of Family Growth” to demonstrate how to use some procedures available in SPSS PC Version 10. Regression analysis allows us to examine the substantive impact of one or more variables on another by using the components of the equation for the "best-fitting" regression line. Once again, while the calculations of these components can be tedious by hand, they are lightning fast with SPSS. Using SPSS for bivariate and multi-variate regression analysis: • Choose Analyze then Regression and then Linear. For a bivariate regression model you just need to specify the dependent variable and the single independent variable in the dialogue box that comes up. Hit "OK." • For example, if I wanted to look at how the educational attainment of the women in our NSFG data is affected by the educational attainment of their mothers, I would enter momed as my independent variable and educ as my dependent variable (would it make sense to switch these?). The syntax for these commands is (first setting values of 95 to missing for momed): missing values momed (95). REGRESSION /MISSING LISTWISE /STATISTICS COEFF OUTS R ANOVA /CRITERIA=PIN(.05) POUT(.10) /NOORIGIN /DEPENDENT educ /METHOD=ENTER momed . Once I hit OK, SPSS automatically kicks out a ton of output on the regression model predicted. • This output allows you to answer a wide variety of questions. • The “Model Summary” and “Anova” boxes give goodness of fit measures and measures of significance for the entire model. -

Can Statistics Do Without Artefacts?
Munich Personal RePEc Archive Can statistics do without artefacts? Chatelain, Jean-Bernard Cournot Centre December 2010 Online at https://mpra.ub.uni-muenchen.de/42867/ MPRA Paper No. 42867, posted 28 Nov 2012 13:21 UTC Can Statistics Do without Artefacts? Jean-Bernard Chatelain1 Prisme N° 19 December 2010 1 Jean-Bernard Chatelain is Professor of Economics at the Sorbonne Economic Centre (Université Paris-I) and Co- director of the CNRS European Research Group on Money, Banking and Finance. His research interests are growth, investment, banking and finance, applied econometrics and statistical methodology. © Cournot Centre, December 2010 Summary This article presents a particular case of spurious regression, when a dependent variable has a coefficient of simple correlation close to zero with two other variables, which are, on the contrary, highly correlated with each other. In these spurious regressions, the parameters measuring the size of the effect on the dependent variable are very large. They can be “statistically significant”. The tendency of scientific journals to favour the publication of statistically significant results is one reason why spurious regressions are so numerous, especially since it is easy to build them with variables that are lagged, squared or interacting with another variable. Such regressions can enhance the reputation of researchers by stimulating the appearance of strong effects between variables. These often surprising effects are not robust and often depend on a limited number of observations, fuelling scientific controversies. The resulting meta-analyses, based on statistical synthesis of the literature evaluating this effect between two variables, confirm the absence of any effect. This article provides an example of this phenomenon in the empirical literature, with the aim of evaluating the impact of development aid on economic growth. -

Sampling Distribution of the Regression Coefficient
The Sampling Distribution of Regression Coefficients. David C. Howell Last revised 11/29/2012 This whole project started with a query about the sampling distribution of the standardized regression coefficient, . I had a problem because one argument was that is a linear transformation of b, and the sampling distribution of b is normal. From that it followed that the sampling distribution of should be normal. On the other hand, with only one predictor, is equal to r, and it is well known that the sampling distribution of r is skewed whenever is unequal to zero. From that it follows that the sampling distribution of would be skewed. To make a long story short, my error was in thinking of as a linear transformation of b—it is not. The formula for is bs ii s0 th where si is the standard deviation of the i independent variable, and s0 is the standard deviation of the dependent (criterion) variable. But in creating the sampling distribution of , these two standard deviations are random variables, differing from sample to sample. If I computed using the corresponding population parameters that would be a different story. But that’s not the way you do it. So my statement about being a linear transformation of was wrong. The unstandardized coefficient (b) is normally distributed, but the standardized coefficient () is not normally distributed. It has the same distribution as r. But all is not right in the world. There is something wrong out there, and I can’t figure out what. I recently received an e-mail from Alessio Toraldo, at Università di Pavia, Italy. -

Subject Index
Subject index Symbols angle() (axis-label suboption) . 124– ∆β . 274–275 125 ∆χ2 ...............................275 ANOVA ..................see regression β ..........see regression, standardized Anscombe quartet . 199, 201, 226 coefficient anycount() (egen function) . 88 *...............see do-files, comments append. .316–319 +........................see operators arithmeticmean...........see average //..............see do-files, comments arithmeticalexpressions............see #delimit . 36–37 expressions &........................see operators ascategory (graph dot option) . 149 N . 82–83, 95 ASCII files . .292–301 all. .47–48 ATS ...............................354 b[ ]..............................185 augmented component-plus-residual plot merge (variable). .310–312 .............204 n . 81–82, 95 autocode() (function).............152 | .........................see operators autocorrelation.........see regression, || ..................................104 autocorrelation ........................see operators average .. 15–16, 153, 156 ~ ........................see operators avplots . 207–208 aweight (weighting type) . 68–69 A axis labels . 107–108, 122–125 Academic Technology Service. .see ATS scales. .117–119 added-variable plot. .206–209 titles . 107–108, 126–127 additiveindex......................79 2 transformations. .118–119 adjusted count R . .266–267 adjusted R2 . .195–196 ado-directories.....................359 B ado-files balanced panel data . .312–313 basics . 335–337 bands() (twoway mband option) . 202– programming .. 337–351 203 -

Multiple Regression
DEPARTMENT OF POLITICAL SCIENCE AND INTERNATIONAL RELATIONS Posc/Uapp 816 MULTIPLE REGRESSION I. AGENDA: A. Standardized regression coefficients B. Multiple regression model. C. Reading: Agresti and Finlay Statistical Methods in the Social Sciences, 3rd edition, Chapter 10 and Chapter 11, 383 to 394. II. STANDARDIZED VARIABLES AND COEFFICIENTS: ˆ A. We have noted several times that the magnitude of b1, or its estimator $1, reflects the units in which X, the independent variable is measured. B. Suppose, for example, we had this equation: ˆ ' % % Yi 10 1.0X1 1000X2 1. Furthermore, suppose X1 is measured in thousands of dollars and X2 is measured in just dollars. ˆ ˆ 2. Note that although $2 is considerably larger than $1 , both variables have the same impact on Y, since a "one-unit" change in X2 (when the other variable is held constant, see below) has effectively the same effect as "one-unit" change in X1. (Changing X2 one unit of course amounts to a dollar change; but because this dollar change is multiplied by 1000 the ˆ effect on Y is 1000, the same as the effect of $1 . Why? 3. In essence, the regression coefficient b1 is measured in units that are units of Y divided by the units of X. C. For this reason and because many measures in the social and policy sciences are often non-intuitive (e.g., attitude scales) coefficients are frequently difficult to compare. 1. Hence, it sometimes useful to rescale all of the variables so that they have a "dimensionless" or common or standard unit of measurement. -
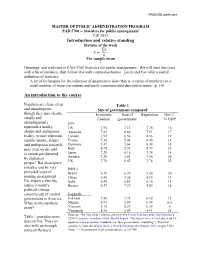
Statistics for Public Management Fall 2013 Introduction and Relative Standing Statistic of the Week
PAD5700 week one MASTER OF PUBLIC ADMINISTRATION PROGRAM PAD 5700 -- Statistics for public management Fall 2013 Introduction and relative standing Statistic of the week ̅ The sample mean * Greetings, and welcome to PAD-5700 Statistics for public management. We will start this class with a bit of statistics, then follow this with course mechanics. Levin and Fox offer a useful definition of statistics: A set of techniques for the reduction of quantitative data (that is, a series of numbers) to a small number of more convenient and easily communicated descriptive terms. (p. 14) An introduction to the course Numbers are clean, crisp Table 1 and unambiguous, Size of government compared though they may clearly, Economic Size of Regulation Gov’t1 crisply and freedom government % GDP unambiguously G7+ represent a murky, US 7.93 7.13 7.78 16 sloppy and ambiguous Australia 7.83 6.80 7.91 17 reality; or may represent Canada 7.92 6.54 8.16 19 equally murky, sloppy France 7.20 5.43 6.45 23 and ambiguous research; Germany 7.47 5.64 6.34 18 may even on the odd Italy 6.75 5.71 5.77 21 occasion get distorted Japan 7.38 6.18 7.34 18 by dishonest Sweden 7.26 3.61 7.16 26 people! But descriptive UK 7.78 6.02 7.76 22 statistics can be very BRICs powerful ways of Brazil 6.18 6.39 5.00 20 making an argument. China 6.44 3.28 5.93 11 For instance, two big India 6.48 6.84 6.16 12 issues in today's Russia 6.57 7.27 5.69 18 political climate concerns out of control Laggards government in America. -

Package 'Misty'
Package ‘misty’ February 26, 2020 Type Package Title Miscellaneous Functions 'T. Yanagida' Version 0.2.2 Date 2020-02-25 Author Takuya Yanagida [aut, cre] Maintainer Takuya Yanagida <[email protected]> Description Miscellaneous functions for data management, descriptive statistics, and statistical analy- sis e.g., reading and writing a SPSS file, frequency table, cross tabulation, multilevel and miss- ing data descriptive statistics, various effect size measures, scale and group scores, center- ing at the grand mean or within cluster, or coefficient alpha and item statistics. Depends R (>= 3.4) License MIT + file LICENSE Imports haven Suggests lme4, mnormt, nlme, plyr, R.rsp VignetteBuilder R.rsp Encoding UTF-8 RoxygenNote 7.0.2 NeedsCompilation no Repository CRAN Date/Publication 2020-02-26 17:10:02 UTC R topics documented: alpha.coef . .3 as.na . .5 center . .7 cohens.d . .9 cont.coef . 12 cor.matrix . 14 cramers.v . 16 1 2 R topics documented: crosstab . 17 descript . 19 df.merge . 21 df.rbind . 23 df.rename . 25 df.sort . 26 dummy.c . 27 eta.sq . 29 freq ............................................. 30 group.scores . 32 kurtosis . 34 multilevel.descript . 35 multilevel.icc . 36 na.as . 38 na.auxiliary . 39 na.coverage . 41 na.descript . 42 na.indicator . 43 na.pattern . 45 na.prop . 46 phi.coef . 47 poly.cor . 48 print.alpha.coef . 50 print.cohens.d . 51 print.cont.coef . 52 print.cor.matrix . 53 print.cramers.v . 54 print.crosstab . 55 print.descript . 56 print.eta.sq . 57 print.freq . 58 print.multilevel.descript . 59 print.na.auxiliary . 60 print.na.coverage .