Bellie Sivakumar Bridging Determinism and Stochasticity
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Copyright by Kristen Dawn Rudisill 2007
Copyright by Kristen Dawn Rudisill 2007 The Dissertation Committee for Kristen Dawn Rudisill certifies that this is the approved version of the following dissertation: BRAHMIN HUMOR: CHENNAI’S SABHA THEATER AND THE CREATION OF MIDDLE-CLASS INDIAN TASTE FROM THE 1950S TO THE PRESENT Committee: ______________________________ Kathryn Hansen, Co-Supervisor ______________________________ Martha Selby, Co-Supervisor ______________________________ Ward Keeler ______________________________ Kamran Ali ______________________________ Charlotte Canning BRAHMIN HUMOR: CHENNAI’S SABHA THEATER AND THE CREATION OF MIDDLE-CLASS INDIAN TASTE FROM THE 1950S TO THE PRESENT by Kristen Dawn Rudisill, B.A.; A.M. Dissertation Presented to the Faculty of the Graduate School of the University of Texas at Austin in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy The University of Texas at Austin December 2007 For Justin and Elijah who taught me the meaning of apu, pācam, kātal, and tuai ACKNOWLEDGMENTS I came to this project through one of the intellectual and personal journeys that we all take, and the number of people who have encouraged and influenced me make it too difficult to name them all. Here I will acknowledge just a few of those who helped make this dissertation what it is, though of course I take full credit for all of its failings. I first got interested in India as a religion major at Bryn Mawr College (and Haverford) and classes I took with two wonderful men who ended up advising my undergraduate thesis on the epic Ramayana: Michael Sells and Steven Hopkins. Dr. Sells introduced me to Wendy Doniger’s work, and like so many others, I went to the University of Chicago Divinity School to study with her, and her warmth compensated for the Chicago cold. -

Sync Sound and Indian Cinema | Upperstall.Com 29/02/12 2:30 PM
Sync Sound and Indian Cinema | Upperstall.Com 29/02/12 2:30 PM Open Feedback Dialog About : Wallpapers Newsletter Sign Up 8226 films, 13750 profiles, and counting FOLLOW US ON RECENT Sync Sound and Indian Cinema Tere Naal Love Ho Gaya The lead pair of the film, in their real life, went in the The recent success of the film Lagaan has brought the question of Sync Sound to the fore. Sync Sound or Synchronous opposite direction as Sound, as the name suggests, is a highly precise and skilled recording technique in which the artist's original dialogues compared to the pair of the are used and eliminates the tedious process of 'dubbing' over these dialogues at the Post-Production Stage. The very first film this f... Indian talkie Alam Ara (1931) saw the very first use of Sync Feature Jodi Breakers Sound film in India. Since then Indian films were regularly shot I'd be willing to bet Sajid Khan's modest personality and in Sync Sound till the 60's with the silent Mitchell Camera, until cinematic sense on the fact the arrival of the Arri 2C, a noisy but more practical camera that the makers of this 'new particularly for outdoor shoots. The 1960s were the age of age B... Colour, Kashmir, Bouffants, Shammi Kapoor and Sadhana Ekk Deewana Tha and most films were shot outdoors against the scenic beauty As I write this, I learn that there are TWO versions of this of Kashmir and other Hill Stations. It made sense to shoot with film releasing on Friday. -

Tla Hearing Board
TLA HEARING BOARD Location : Chennai Hearing Schedule from 01/09/2021 to 30/09/2021 Dated : 06/08/2021 10:15:28 S.No TM No Class Hearing Proprietor Name Agent Name Mode of Date Hearing 1 4345947 19 01-09-2021 M/s. ANR DESIGNER TILES LIMITED SUNEER AND ASSOCIATES video conferencing 2 4450520 14 01-09-2021 MUAAD MOHAMMED ASHRAF SUNEER AND ASSOCIATES video conferencing 3 4450522 35 01-09-2021 MUAAD MOHAMMED ASHRAF SUNEER AND ASSOCIATES video conferencing 4 4450526 29 01-09-2021 MAJEED PULLANCHERI SUNEER AND ASSOCIATES video conferencing 5 4439076 24 01-09-2021 SARAVAN TEX L.R. SWAMI CO. video conferencing 6 4430578 5 01-09-2021 DR. REDDY'S LABORATORIES LIMITED TRADING AS DR. REDDY'S LABORATORIES video conferencing MANUFACTURER AND TRADER LIMITED TRADING AS MANUFACTURER AND TRADER 7 4425495 5 01-09-2021 TABLETS (INDIA) LIMITED TABLETS (INDIA) LIMITED video conferencing 8 4457725 41 01-09-2021 THG Publishing Private Limited MOHAN ASSOCIATES. video conferencing 9 4430600 30 01-09-2021 C.MUTHUKUMARASWAMI P. C .N. RAGHUPATHY. video conferencing 10 1328727 5 01-09-2021 K. N. BIOSCIENCES (INDIA) PVT. LTD RAO & RAO. video conferencing 11 4341141 41 01-09-2021 M/S. MARIGOLD CREATIVE PVT. LTD SUNEER AND ASSOCIATES video conferencing 12 4427219 14 01-09-2021 GRT JEWELLERS (INDIA) PRIVATE LIMITED L.R. SWAMI CO. video conferencing 13 4427237 14 01-09-2021 GRT JEWELLERS (INDIA) PRIVATE LIMITED L.R. SWAMI CO. video conferencing 14 4427239 14 01-09-2021 GRT JEWELLERS (INDIA) PRIVATE LIMITED L.R. SWAMI CO. -

Moore Leaves ‘Can You Ever Forgive Me’ Ulianne Moore Has Exited Nicole Actual Letters from Library Archives and Jholofcener’S Drama “Can You Ever Sold Them
Lifestyle FRIDAY, JULY 17, 2015 Moore leaves ‘Can You Ever Forgive Me’ ulianne Moore has exited Nicole actual letters from library archives and JHolofcener’s drama “Can You Ever sold them. In 1993, Israel pleaded guilty Forgive Me” due to creative differ- to conspiracy to transport stolen proper- ences, Variety has learned exclusively. ty and served six months under house The Fox Searchlight project, also starring arrest. She died last year. Chris O’Dowd, had been set to start The film would have been Moore’s shooting in about a week and executives first since her best actress Oscar win for have begun seeking a replacement for “Still Alice.” She will be seen next in Moore. Anne Carey is producing. October in the drama “Freeheld” with Holofcener is directing from her own Ellen Page and Steve Carell and in script, based on the 2008 memoir of the November in “The Hunger Games: same name by journalist Mockingjay-Part 2.” Lee Israel. In 1992, Israel had fallen on Moore has also completed production hard times and began selling letters that on romantic comedy “Maggie’s Plan,” she had forged from deceased writers which also stars Greta Gerwig, Ethan and actors. When the forgeries started to Hawke, Bill Hader, Maya Rudolph and raise suspicion, she turned to stealing the Monte Greene. — Reuters Julianne Moore Disney developing live-action ‘Aladdin’ prequel isney is developing “Genies,” a movie for Disney. (Fun fact: Vinson’s Day” with Peter Dinklage starring. Jake Gyllenhaal and Naomi Watts Dlive-action comedy prequel to its bachelor party was true-life inspiration Disney has been mining its library 1992 animated hit for 2009’s “The Hangover.”) of animated movies for live-action “Aladdin.”Tripp Vinson is on board to Shannon and Swift’s credits inspiration, evidenced by recent Gyllenhaal, Watts drama produce “Genies” through his Vinson include 2009’s “Friday the reboots “Cinderella,” “Maleficent,” Films banner. -

VOLVIV February 2015 No. 2 HIGHLIGHTS
VOLVIV February 2015 No. 2 HIGHLIGHTS Kukunoor’s Dhanak bags Berlin honour India’s 175 Grams wins at Sundance Film Festival Bodhon wins two awards in US Film Festival Mardaani premieres in Poland D. Rama Naidu is no more NATIONAL DOCUMENTATION CENTRE ON MASS COMMUNICATION NEW MEDIA WING (FORMERLY RESEARCH, REFERENCE AND TRAINING DIVISION ) MINISTRY OF INFORMATION AND BROADCASTING Room No.437-442, Phase IV, Soochana Bhavan, CGO Complex, New Delhi-3 Compiled, Edited & Issued by National Documentation Centre on Mass Communication NEW MEDIA WING (Formerly Research, Reference & Training Division) Ministry of Information & Broadcasting Chief Editor L. R. Vishwanath Editor H.M.Sharma Asstt. Editor Alka Mathur CONTENTS FILM AWARDS International 1-2 FESTIVALS Berlin 1 North Carolina 2 Sundance 1-2 OBITUARIES 2-5 AWARDS/FESTIVALS Kukunoor’s Dhanak bags Berlin honour Filmmaker Nagesh Kukunoor’s Dhanak has been honoured with the Grand Prix of the Generation K plus International Jury for the best feature length film at the 65th Berlin International Film Festival. The movie which premiered at the festival, also received a special mention from kids jury at the festival. Dhanak is about a young girl in Rajasthan who is determined to restore the vision of her blind brother. The film stars Hetal Gada and Krrish Chhabria. Co-produced by Manish Mundra, Kukunoor and Elahe Hiptoola, the film had its world premiere at the Berlinale held from February 5 to 15, 2015. Screen (20 February 2015; 12) Dainik Jagran (16 February 2015) Asian Age (16 February 2015) Hindustan Times (19 February 2015) India’s 175 Grams wins at Sundance Film Festival Indian film 175 Grams directed by Bharat Mirle and Arvind Iyer is one of the five winners of the Short Film Challenge programme at the 2015 Sundance Film Festival at Park City in Utah. -

We Refer to Reserve Bank of India's Circular Dated June 6, 2012
We refer to Reserve Bank of India’s circular dated June 6, 2012 reference RBI/2011-12/591 DBOD.No.Leg.BC.108/09.07.005/2011-12. As per these guidelines banks are required to display the list of unclaimed deposits/inoperative accounts which are inactive / inoperative for ten years or more on their respective websites. This is with a view of enabling the public to search the list of accounts by name of: Cardholder Name Address Ahmed Siddiq NO 47 2ND CROSS,DA COSTA LAYOUT,COOKE TOWN,BANGALORE,560084 Vijay Ramchandran CITIBANK NA,1ST FLOOR,PLOT C-61, BANDRA KURLA,COMPLEX,MUMBAI IND,400050 Dilip Singh GRASIM INDUSTRIES LTD,VIKRAM ISPAT,SALAV,PO REVDANDA,RAIGAD IND,402202 Rashmi Kathpalia Bechtel India Pvt Ltd,244 245,Knowledge Park,Udyog Vihar Phase IV,Gurgaon IND,122015 Rajeev Bhandari Bechtel India Pvt Ltd,244 245,Knowledge Park,Udyog Vihar Phase IV,Gurgaon IND,122015 Aditya Tandon LUCENT TECH HINDUSTAN LTD,G-47, KIRTI NAGAR,NEW DELHI IND,110015 Rajan D Gupta PRICE WATERHOUSE & CO,3RD FLOOR GANDHARVA,MAHAVIDYALAYA 212,DEEN DAYAL UPADHYAY MARG,NEW DELHI IND,110002 Dheeraj Mohan Modawel Bechtel India Pvt Ltd,244 245,Knowledge Park,Udyog Vihar Phase IV,Gurgaon IND,122015 C R Narayan CITIBANK N A,CITIGROUP CENTER 4 TH FL,DEALING ROOM BANDRA KURLA,COMPLEX BANDRA EAST,MUMBAI IND,400051 Bhavin Mody 601 / 604, B - WING,PARK SIDE - 2, RAHEJA,ESTATE, KULUPWADI,BORIVALI - EAST,MUMBAI IND,400066 Amitava Ghosh NO-45-C/1-G,MOORE AVENUE,NEAR REGENT PARK P S,CALCUTTA,700040 Pratap P CITIBANK N A,NO 2 GRND FLR,CLUB HOUSE ROAD,CHENNAI IND,600002 Anand Krishnamurthy -
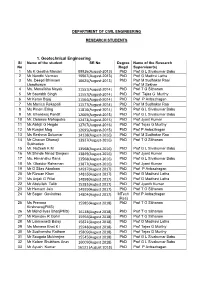
1. Geotechnical Engineering 14128
DEPARTMENT OF CIVIL ENGINEERING RESEARCH STUDENTS 1. Geotechnical Engineering Sl Name of the student SR No Degree Name of the Research No Regd Supervisor(s) 1 Ms K Geetha Manjari 08826(August-2013) PhD Prof G L Sivakumar Babu 2 Mr Nandhi Varman 10567(August-2013) PhD Prof G Madhvi Latha 3 Ms. Deepti Bhimsen 10625(August-2013) PhD Prof M Sudhakar Rao/ Upadhyaya Prof M Sekhar 4 Ms. Monalisha Nayak 11551(August-2014) PhD Prof T G Sitharam 5 Mr Saurabh Singh 11557(August-2014) PhD Prof Tejas G Murthy 6 Mr Ketan Bajaj 11564(August-2014) PhD Prof P Anbazhagan 7 Ms Monica Rekapalli 11577(August-2014) PhD Prof M Sudhakar Rao 8 Ms Pinom Ering 11816(August-2014) PhD Prof G L Sivakumar Babu 9 Mr. Bhardwaj Pandit 12669(August-2015) PhD Prof G L Sivakumar Babu 10 Mr. Debasis Mohapatra 12473(August-2015) PhD Prof Jyant Kumar 11 Mr.Abhijit G Hegde 12707(August-2015) PhD Prof Tejas G Murthy 12 Mr Kunjari Mog 12695(August-2015) PhD Prof P Anbazhagan 13 Ms Reshma Sukumar 14128(August-2016) PhD Prof M Sudhakar Rao 14 Mr Chavan Dhanaji 13927(August-2016) PhD Prof T G Sitharam Sukhadeo 15 Mr. Nazeeh K M 13568(August-2016) PhD Prof G L Sivakumar Babu 16 Mr.Shinde Ninad Sanjeev 13849(August-2016) PhD Prof Jyant Kumar 17 Ms. Himanshu Rana 13568(August-2016) PhD Prof G L Sivakumar Babu 18 Mr. Obaidur Rahaman 13877(August-2016) PhD Prof Jyant Kumar 19 Mr G Silas Abraham 14937(August 2017) PhD Prof P Anbazhagan 20 Mr Rizwan Khan 14816(August 2017) PhD Prof G Madhavi Latha 21 Ms Anjali G Pillai 14898(August 2017) PhD Prof G Madhavi Latha 22 Mr Abdullah Talib 15281(August -

Dr. NARAYANA NAGESH Educational Details. Professional Details. Research Interests and Area of Expertise. Researc
Dr. NARAYANA NAGESH Chief Scientist, CCMB, Hyderabad-500007, Telangana, India. Date of birth: 31-10-1964, Male. Address for Correspondence: Dr. N. Nagesh, Chief Scientist , Centre for Cellular and Molecular Biology, Uppal Road, Hyderabad-500 007, Telangana. India. Phone: + 91- 040 – 27195563 (Office) FAX : 040-27160591 ; 040-27160311 [email protected] or [email protected] http://e-portal.ccmb.res.in/e-space/nagesh/index.html Educational Details. Doctor of Philosophy (PhD.,) : From S.V. University, Tirupati, A.P., India. “Studies on the Structure and Interaction of G-Quadruplex DNA with Metal Ions and Drugs”. Post-Doctorate : With Prof. Edwin A Lewis, Department of Chemistry at North Arizona University, Flagstaff, Arizona, USA. “Studies on Bcl2 Quadruplex DNA interaction with Porphyrins”. Professional Details. Joined CCMB as Scientist-B in the year 1990. Serving CCMB now as Chief Scientist. Research interests and Area of expertise. Interested in the studies involving G-quadruplex DNA and its interaction with metals, macromolecules, ligands. Synthesis and identification of novel organic and inorganic complexes that will improve anti- cancer, pro-apoptotic and anti-cancer cell proliferation activity both under in vitro and in vivo conditions by topological, pharmacophores modification of synthetic molecules. Biophysics, Biochemistry, Chemistry, Medicinal Chemistry and Chemical Biology. Research Projects. I. Projects completed. Successfully completed Indo-Swiss Joint Research Project (ISJRP) 2012-15 ; A project from DST, 2012-15; NanoSHE project: (a XII FYP project) Project obtained from CSIR; One FTT and Misson Mode project from CSIR, 2017-2020. II. Projects in progress: Having one FTT (from 2020-2022), Project title -“Homocysteine Specific Novel Sensor for Diagnostic Use”. -

Spoofs and the Politics of the Film Image's Ontology in Tamil Cinema
Spoofs and the Politics of the Film Image’s Ontology in Tamil Cinema * Constantine V. Nakassis All Film Spoofs, No Spoof Films Commercial Tamil cinema has long been a travesty of itself, its textuality woven from so many citational allusions, homages, and self-parodies; and yet, until recently there was no such recognized genre of the spoof film, only “comedy tracks” trailing in the shadows of the grandiose hero and his more serious narrative, parodying his potent image here and there, most often through scenes of comically inverted or failed heroism (Nakassis 2010:209–221). In 2010, this was seen to have changed, with the release of a surfeit of spoof films—Venkat Prabhu’s Goa, Simbudevan’s Irumbu Kottai Mirattu Singam, and, most importantly for this paper, C. S. Amudhan’s aptly titled Thamizh Padam, or ‘Tamil Movie.’1 And then of course, there was that unwitting spoof hero, the self-proclaimed “Power Star,” Dr. S. Srinivasan, who entered the scene in 2011 with his unbel- ievably absurd, yet ambiguously self-serious, film (Lathika) and public persona (figure 1).2 Industry insiders and film enthusiasts often explain this seeming par- adox that Tamil cinema is all spoof with no spoofs by pointing to the self- seriousness of the industry—that is, that it can’t take a joke; or alter- natively by pointing to its cultural and historical particularity—that is, that “spoofs” are a foreign genre. But what is so notable is that the ind- ustry has long made jokes at its own expense. Think, for example, of Nagesh’s memorable comedy track from Sridhar’s classic 1964 romantic comedy Kadhalikka Neeramillai (‘No Time for Love’), which turns on Nagesh’s nascent film production: a parody of the film producer, Nagesh * Constantine V. -

Accused Persons Arrested in District from To
Accused Persons arrested in district from to Name of Name of the Name of the Place at Date & Arresting Court at Sl. Name of the Age & Cr. No & Sec Police father of Address of Accused which Time of Officer, which No. Accused Sex of Law Station Accused Arrested Arrest Rank & accused Designation produced 1 2 3 4 5 6 7 8 9 10 11 Chirayil House, 22.09.2019 1098/19 U/s 15 K N Manoj ,SI Bail from 1 Kurian Varghese 45 M Eramalloor P O, Eramalloor Aroor 13.00 Hrs (C) of KA Act of Police Station Ezhupunna P/W 11 1099/19 U/s 279 Vattathara House,Aroor 22.09.2019 K N Manoj ,SI Bail from 2 Maneesh Bhaskaran 29 M Chandiroor IPC 185 of MV Aroor P O, Aroor P/W 13 19.15 Hrs of Police Station Act Asariparambu House, 1100 /2019 U/s 22.09.2019 K N Manoj ,SI Bail from 3 Viswambharan Rajappan 59 M Kumbalam P O, Aroor 118 (a) of KP Aroor 20.45 Hrs of Police Station Kumbalam P/W 14 Act 1101/2019 U/s Pulloorikkal, Arookutty 22.09.2019 K N Manoj ,SI Bail from 4 Rahul Ullas 27 M Aroor 279 IPC 185 of Aroor P O, Aroorkutty P/W 13` 21.10 Hrs of Police Station MV Act Chembath, Ezhumangad 1102/2019 U/s 22.09.2019 K N Manoj ,SI Bail from 5 Shijith Ramachandran 38 M P O, Thiruritacode P O, Chandiroor 279 IPC & 185 Aroor 22.55 Hrs of Police Station Palakkad of MV Act Rajamallil house, 1105/2019 U/s Kadeparambikiyal, 23.09.2019 K N Manoj ,SI Bail from 6 Hemanth Haridas 24 M Eramalloor 279 IPC & 185 Aroor Pallippuram P O, 19.00 Hrs of Police Station of MV Act Cherthala Mulackal parambu 1108/2019 U/s 23.09.2019 K N Manoj ,SI Bail from 7 Purushan Madhavan 52 M House, Aroor -

Born Kamal Haasan 7 November 1954 (Age 56) Paramakudi, Madras State, India Residence Chennai, Tamil Nadu, India Occupation Film
Kamal Haasan From Wikipedia, the free encyclopedia Kamal Haasan Kamal Haasan Born 7 November 1954 (age 56) Paramakudi, Madras State, India Residence Chennai, Tamil Nadu, India Occupation Film actor, producer, director,screenwriter, songwriter,playback singer, lyricist Years active 1959–present Vani Ganapathy Spouse (1978-1988) Sarika Haasan (1988-2004) Partner Gouthami Tadimalla (2004-present) Shruti Haasan (born 1986) Children Akshara Haasan (born 1991) Kamal Haasan (Tamil: கமலஹாசன்; born 7 November 1954) is an Indian film actor,screenwriter, and director, considered to be one of the leading method actors of Indian cinema. [1] [2] He is widely acclaimed as an actor and is well known for his versatility in acting. [3] [4] [5] Kamal Haasan has won several Indian film awards, including four National Film Awards and numerous Southern Filmfare Awards, and he is known for having starred in the largest number of films submitted by India in contest for the Academy Award for Best Foreign Language Film.[6] In addition to acting and directing, he has also featured in films as ascreenwriter, songwriter, playback singer, choreographer and lyricist.[7] His film production company, Rajkamal International, has produced several of his films. In 2009, he became one of very few actors to have completed 50 years in Indian cinema.[8] After several projects as a child artist, Kamal Haasan's breakthrough into lead acting came with his role in the 1975 drama Apoorva Raagangal, in which he played a rebellious youth in love with an older woman. He secured his second Indian National Film Award for his portrayal of a guileless school teacher who tends a child-like amnesiac in 1982's Moondram Pirai. -

F.No.29101L2017-SR(S) Government of India Ministry of Personnel, PG and Pensions Departmental of Personnel of Training *****
F.No.29101l2017-SR(S) Government of India Ministry of Personnel, PG and Pensions Departmental of Personnel of Training ***** 3rd Floor, Lok Nayak Bhawan, Khan Market, New Delhi Dated: 22nd February 2017 Order No.10(4)/2017 The Government of India, drawing powers conferred under Section 77 (2) of the AP Reorganisation Act, 2014, hereby allocates all the State Cadre employees of the Director of Health, Department of Health, Medical & Family Welfare who, immediately before 02.06.2014, were working in connection with the affairs of Government of Andhra Pradesh and have been recommended for allocation to Andhra Pradesh 1 Telangana by the Advisory Committee vide Lr. No.625/SRII AI12015 dated 22.12.2016, to the respective States, with effect from 02.06.2014. The lists of employees allocated to AP & TS are at Annexure I and Annexure II respectively. 2. Provided that this order will not come into effect in respect of any person who has obtained 'stay order' from a Court of Law against his allocation to any of the Successor State, till the time such stay order is vacated. 3. Provided further that any person who has not been allocated under Section 77 (2) of the AP Reorganisation Act, 2014, shall continue to work in his present State, till allocation order is passed by the Government of India as per the recommendations of the Advisory Committee in accordance with the extant rules. Encl: List of employees allocated to Andhra Pradesh (3828)1 Telangana (2470). ~ 2-)...- 2-- \J (R. Venkatesan) Under Secretary to the Government of India To 1.