Dragonfly Optimization Based Reconfiguration for Voltage Stability Enhancement in Distribution Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Accused Persons Arrested in Eranakulam Rural District from 03.08.2014 to 09.08.2014
Accused Persons arrested in Eranakulam Rural district from 03.08.2014 to 09.08.2014 Name of Name of the Name of the Place at Date & Arresting Court at Sl. Name of the Age & Cr. No & Sec Police father of Address of Accused which Time of Officer, Rank which No. Accused Sex of Law Station Accused Arrested Arrest & accused Designation produced 1 2 3 4 5 6 7 8 9 10 11 Pazhampilly 643/14 U/s-279 JFCMC North 1 Unni Thomas 51/14 (h)Karothukunnu,Muppa Idukki Jn 4.8.2014 Binanipuram P.V.poulose,SI IPC 185 MvAct Paravoor thadom Vylokuzhi West 644/14 U/s-279 JFCMC North 2 Jinob Gopi 30/14 (H)Muppathadom,Kadun 4.8.2014 Binanipuram P.V.poulose,SI Kadungalloor IPC 185 MvAct Paravoor galloor Pappara Parambu 647/14 U/s- JFCMC North 3 Abdul Rahman Kochu Moidheen 60/14 House,Panaikulam,Alang Panaikulam 6.8.2014 118(i) KPACT & Binanipuram MM jose, GSI Paravoor adu 6 r/w 21 of Cotpa Puthuval parambu (H) Cr.No.6648/14, Kaniyamkunnu JFCMC North 4 Sivadas Maniyan 42/14 ,Kaniyamkunnu, East 6.8.2014 U/s 279,185MV Binanipuram MM jose, GSI Jn Paravoor Kadfungalloor Act Mulavarickal House, 649/14 U/s- 279 JFCMC North 5 Jose Mani Mani 50/14 Elapadom 7.8.2014 Binanipuram PV Poulose, SI Aduvassery, Kunnukara IPC 185 MvAct Paravoor Moolaparambil 650/14 U/s- 279 JFCMC North 6 Sabu Kumaran 44/14 house.Manjummal kara, Edayar 7.8.2014 Binanipuram PV Poulose, SI IPC 185 MvAct Paravoor eloor Sarangi house, 651/14 U/s- 279 JFCMC North 7 Aji Krishnapilla 49/14 Maniyelipadi, Valanjambalam 8.8.2014 Binanipuram PV Poulose, SI IPC 185 MvAct Paravoor Kadungalloor Thadakal 652/14 -

Payment Locations - Muthoot
Payment Locations - Muthoot District Region Br.Code Branch Name Branch Address Branch Town Name Postel Code Branch Contact Number Royale Arcade Building, Kochalummoodu, ALLEPPEY KOZHENCHERY 4365 Kochalummoodu Mavelikkara 690570 +91-479-2358277 Kallimel P.O, Mavelikkara, Alappuzha District S. Devi building, kizhakkenada, puliyoor p.o, ALLEPPEY THIRUVALLA 4180 PULIYOOR chenganur, alappuzha dist, pin – 689510, CHENGANUR 689510 0479-2464433 kerala Kizhakkethalekal Building, Opp.Malankkara CHENGANNUR - ALLEPPEY THIRUVALLA 3777 Catholic Church, Mc Road,Chengannur, CHENGANNUR - HOSPITAL ROAD 689121 0479-2457077 HOSPITAL ROAD Alleppey Dist, Pin Code - 689121 Muthoot Finance Ltd, Akeril Puthenparambil ALLEPPEY THIRUVALLA 2672 MELPADAM MELPADAM 689627 479-2318545 Building ;Melpadam;Pincode- 689627 Kochumadam Building,Near Ksrtc Bus Stand, ALLEPPEY THIRUVALLA 2219 MAVELIKARA KSRTC MAVELIKARA KSRTC 689101 0469-2342656 Mavelikara-6890101 Thattarethu Buldg,Karakkad P.O,Chengannur, ALLEPPEY THIRUVALLA 1837 KARAKKAD KARAKKAD 689504 0479-2422687 Pin-689504 Kalluvilayil Bulg, Ennakkad P.O Alleppy,Pin- ALLEPPEY THIRUVALLA 1481 ENNAKKAD ENNAKKAD 689624 0479-2466886 689624 Himagiri Complex,Kallumala,Thekke Junction, ALLEPPEY THIRUVALLA 1228 KALLUMALA KALLUMALA 690101 0479-2344449 Mavelikkara-690101 CHERUKOLE Anugraha Complex, Near Subhananda ALLEPPEY THIRUVALLA 846 CHERUKOLE MAVELIKARA 690104 04793295897 MAVELIKARA Ashramam, Cherukole,Mavelikara, 690104 Oondamparampil O V Chacko Memorial ALLEPPEY THIRUVALLA 668 THIRUVANVANDOOR THIRUVANVANDOOR 689109 0479-2429349 -

Form IEPF-4 SIIL 23267
Note: This sheet is applicable for uploading the particulars related to the shares transferred to Investor Education and Protection Fund. Make sure that the details are in accordance with the information already provided in e-form IEPF-4. CIN L13209MH1965PLC291394Prefill Company Name VEDANTA LIMITED Nominal value of shares 1568170.00 Validate Clear Is the shares Actual Date of Date of Birth(DD- Is the Investment Investor First Investor Middle Investor Last Father/Husband Father/Husband Father/Husband Last DP Id-Client Id- Nominal value of Joint Holder transfer from Address Country State District Pin Code Folio Number Number of shares transfer to IEPF (DD- PAN MON-YYYY) Aadhar Number Nominee Name Remarks (amount/shares) Name Name Name First Name Middle Name Name Account Number shares Name unpaid suspense MON-YYYY) under any litigation account AJIT SINGH NARULA MOHINDER SINGH NARULA 12/31 B L/S, G/F TILAK NAGAR DELHI INDIADELHI DELHI NEW DELHI 110018 C12010600-12010600-00693183 19 19.00 20-SEP-2019 AAEPN9710C 01-JAN-1960 MANJITKAUR NA No No AT-SRIRAMPURI NH-28 BHAGWANPUR INFRONT OF JHAJI C12010600-12010600- RAMA KANT SINGH NAGENDRA SINGH INDIA BIHAR MUZAFFARPUR 842001 60 60.00 20-SEP-2019 AIUPS3027K 03-JUN-1949 PAWANDEVI NA No No PETROL PUMP MUZAFFARPUR 00918954 BIHAR DIST MINORITIES WELFARE C12010600-12010600- ARUN KUMAR YADAVA RAM SUMIRAN YADAV OFFICER FAIZABAD JAUNPUR INDIA UTTAR PRADESH JAUNPUR 224501 60 60.00 20-SEP-2019 ABMPY1013A 19-DEC-1973 SAROJYADAV NA No No 01044952 UTTAR PRADESH H. NO 284/5 KILOD PANA C12010600-12010600- KARAMPAL -

Vmedulife Digital Platform
ILAHIA COLLEGE OF ENGINEERING AND TECHNOLOGY Aisha Meethian (M.Tech Applied electronic) NIJABMANZIL , KIZHAKKEKARA 686661 MUVATTUPUZHA, ERNAKULAM (DIST) +9645722210 [email protected] Qualifications Qualifications Course Institution University CompletionDate / Status Post-Graduation Applied Ilahia College Of M.G University, 10 Jun 2013 Electronics Engineering Kottayam. Graduation Electrical Sree Narayana M.G University, 20 Jun 2011 Gurukulam College of Kottayam. engineering, Kolenchery , Ernakulum, kerala Professional Experience Duration Exprience Status Organization Department Designation Keyareas 01 Aug 01 Years, Currently Ilahia Department Assistant Control 2019-14 3 Months, Associated College of of EEE Professor System Nov 2020 13 Days Engineering Advanced & Control Technology, Theory Mulavoor, Muvattupuzha. Duration Exprience Status Organization Department Designation Keyareas 27 Jan 05 Years, Previously Ilahia Department Assistant Digital 2014-31 6 Months, Working School of of EEE Professor System and Jul 2019 4 Days Science Computer And Organization, Technology Linear , Control Pezhakkappilly, System, Muvattupuzha Advanced Control Theory, Measurements and Measuring Instruments, AcademicsMatlab 2011AcademicsE CADD Research Publications: Publication Type: ResearchPublications Title: Real Time Gesture Recognition Using Gaussian Mixture Model Indexed In: Other Event Status: International Main Author: AISHA MEETHIAN Co-Author: B.M IMRAM Journal Name: IJSER Date: 2013-08-21 UGCapproval: Approved ISSN No: 2229-5518 Volume: Volume 4, Issue: -

LIST of EMPANELLED HOSPITALS Regional Centre City Name Of
LIST OF EMPANELLED HOSPITALS Regional Centre City Name of Hospital/Diag Address Phone/Mob/Email Approved Date of MOA Vaild Recognized for Status of hospital Status of hospital nostic/Dental Centre by MoD Signing up to as per MoA as per Govt letter MOA 1280 KOCHI Alappuzha Sahrudaya Hospital Thathampally Alappuzha - Sister Mini-Administrator, Contact- 04-Jan-08 24-Oct-12 23-Oct-13 General Medicine, General Surgery and Obstetrics and -- NON NABH NON NABH 688013. 04772252269, 04772412005, Email- Gynaecology [email protected] 1281 KOCHI Alappuzha HUDA Trust Hospital Kumara Puram, PO - Mr sahabudeen-Dir, Dr Basheer, 04-Jan-08 30-Nov-13 29-Nov-14 General Medicine, Orthopaedics, Microbiology, General Surgery -- NON NABH NON NABH Danapadi, Haripad, Alappey, Mr T Muhammad Kunju, Contact- and Obstetrics and Gynaecology Haripad - 690548. 04792404466, 9895112005, 9747931425, Email- [email protected] 1282 KOCHI Alappuzha KVM Hospital PB No-30, Cherthala 04-Jan-08 General Medicine, ENT, Orthopaedics, Dental, Microbiology, -- NON NABH NON NABH Alappuzha Cherthala - General Surgery, Opthalmology, Psychiatry, Blood Bank (only 688524. Blood Transfusion), Obstetrics & Gynaecology, Paediatrics, Pathology and Radio Diagnosis. 1283 KOCHI Alappuzha MSGR Joseph Kandathil Green Gardens Mathilakam, 27-Aug-13 10-Oct-13 09-Oct-14 Cancer Hospital : Plastic and Reconstructive Surgery, Surgical NON NABH NON NABH Memorial Cancer Research Cherthala – 688524, Oncology, Medical Oncology & Radiotherapy. Centre (Prathyasa), Distt-Alappuzha, Kerala Laboratory Services : Clinical Pathology and Biochemistry. NON NABH Imaging Services : X-ray, USG, USG Doppler & CT Scan. 1284 KOCHI Calicut KMCT Medical College and KMCT MCH, West Mampetta, 12-Dec-13 General Services : General Medicine, General Surgery, NON NABH NON NABH Hospital Manassery P.O, Mukkom, Obstetrics and Gynaecology, Paediatrics, Orthopaedics, ICU and Calicut – 673602 Critical Care Units, ENT, Ophthalmology, Dermatology, Psychiatry NON NABH and Blood Bank (Blood Transfusion). -

Muvattupuzha Assembly Kerala Factbook
Editor & Director Dr. R.K. Thukral Research Editor Dr. Shafeeq Rahman Compiled, Researched and Published by Datanet India Pvt. Ltd. D-100, 1st Floor, Okhla Industrial Area, Phase-I, New Delhi- 110020. Ph.: 91-11- 43580781, 26810964-65-66 Email : [email protected] Website : www.electionsinindia.com Online Book Store : www.datanetindia-ebooks.com Report No. : AFB/KR-086-0619 ISBN : 978-93-5313-581-2 First Edition : January, 2018 Third Updated Edition : June, 2019 Price : Rs. 11500/- US$ 310 © Datanet India Pvt. Ltd. All rights reserved. No part of this book may be reproduced, stored in a retrieval system or transmitted in any form or by any means, mechanical photocopying, photographing, scanning, recording or otherwise without the prior written permission of the publisher. Please refer to Disclaimer at page no. 119 for the use of this publication. Printed in India No. Particulars Page No. Introduction 1 Assembly Constituency -(Vidhan Sabha) at a Glance | Features of Assembly 1-2 as per Delimitation Commission of India (2008) Location and Political Maps Location Map | Boundaries of Assembly Constituency -(Vidhan Sabha) in 2 District | Boundaries of Assembly Constituency under Parliamentary 3-9 Constituency -(Lok Sabha) | Town & Village-wise Winner Parties- 2019, 2016, 2014, 2011 and 2009 Administrative Setup 3 District | Sub-district | Towns | Villages | Inhabited Villages | Uninhabited 10-11 Villages | Village Panchayat | Intermediate Panchayat Demographics 4 Population | Households | Rural/Urban Population | Towns and Villages -

Department of Industries & Commerce District
Industrial Potential Survey of Ernakulam District GOVERNMENT OF KERALA DEPARTMENT OF INDUSTRIES & COMMERCE DISTRICT INDUSTRIES CENTRE ERNAKULAM POTENTIAL SURVEY REPORT FOR MSME SECTOR Prepared and Published by DISTRICT INDUSTRIES CENTRE KUNNUMPURAM CIVIL STATION ROAD,KAKKANAD,ERNAKULAM PH: 0484-2421432,2421461,FAX – 0484 2421461 E mail- [email protected], [email protected] Web site: www.dic.kerala.gov.in 1 Prepared & Submitted by District Industries Centre,Ernakulam Industrial Potential Survey of Ernakulam District PREFACE An Industrial Potential Survey of Ernakulam District, the industrial capital of Kerala, definitely will be a reflection of the State as a whole. The report is prepared mostly on the basis of available information in different sectors. The survey report reveals the existing industrial scenario of the district and it mainly aims to unveil the potentially disused areas of the industry in Ernakulam. We hope this document will provide guidance for those who need to identify various potential sources/ sectors of industry and thereby can contribute industrial development of the district, and the state. I hereby acknowledge the services rendered by all Managers, Assistant District Industries Officers , Industries Extension Officers ,Statistical Wing and other officers of this office ,for their sincere effort and whole hearted co- operation to make this venture a success within the stipulated time. I am grateful to all the officers of other departments who contributed valuable suggestions and information to prepare this report. General Manager, District Industries Centre, Ernakulam. 2 Prepared & Submitted by District Industries Centre,Ernakulam Industrial Potential Survey of Ernakulam District INDEX Contents Page No Scope & Objectives Methodology Chapter I District at a glance 1.1 Introduction 1.2 Location and extent 1.3 District at a glance 2. -
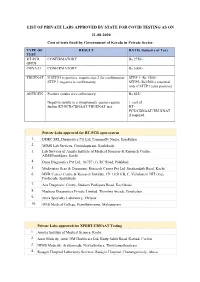
LIST of PRIVATE LABS APPROVED by STATE for COVID TESTING AS on 21-08-2020 Cost of Tests Fixed by Government of Kerala in Private Sector
LIST OF PRIVATE LABS APPROVED BY STATE FOR COVID TESTING AS ON 21-08-2020 Cost of tests fixed by Government of Kerala in Private Sector. TYPE OF RESULT RATE( Inclusive of Tax) TEST RT-PCR CONFIRMATORY Rs 2750/- OPEN CBNAAT CONFIRMATORY Rs 3000/- TRUENAT If STEP1 is positive, require step 2 for confirmation STEP 1- Rs 1500/- STEP 1 negative is confirmatory STEP2- Rs1500/-( required only if STEP1 turns positive) ANTIGEN Positive results are confirmatory. Rs 625/- Negative results in a symptomatic person require + cost of further RT-PCR/CBNAAT/TRUENAT test RT- PCR/CBNAAT/TRUENAT if required Private Labs approved for RT-PCR open system 1. DDRC SRL Diagnostics Pvt Ltd, Panampilly Nagar, Ernakulam 2. MIMS Lab Services, Govindapuram, Kozhikode 3. Lab Services of Amrita Institute of Medical Sciences & Research Centre, AIMSPonekkara, Kochi 4. Dane Diagnostics Pvt Ltd, 18/757 (1), RC Road, Palakkad 5. Medivision Scan & Diagnostic Research Centre Pvt Ltd, Sreekandath Road, Kochi 6. MVR Cancer Centre & Research Institute, CP 13/516 B, C, Vellalaserri NIT (via), Poolacode, Kozhikode 7. Aza Diagnostic Centre, Stadium Puthiyara Road, Kozhikode 8. Neuberg Diagnostics Private Limited, Thombra Arcade, Ernakulam 9. Jeeva Specialty Laboratory, Thrissur 10. MES Medical College, Perinthalmanna, Malappuram Private Labs approved for XPERT/CBNAAT Testing 1. Amrita Institute of Medical Science, Kochi 2. Aster Medcity, Aster DM Healthcare Ltd, Kutty Sahib Road, Kothad, Cochin 3. NIMS Medicity, Aralumoodu, Neyyattinkara, Thiruvananthapuram 4. Rajagiri Hospital Laboratory Services, Rajagiri Hospital, Chunangamvely, Aluva 5. Micro Health LAbs, MPS Tower, Kozhikode 6. Believers Church Medical College Laboratory, St Thomas Nagar, Kuttapuzha P.O., Thiruvalla 7. -

List of Registered Plastic Recycling Units in Kerala
LIST OF REGISTERED PLASTIC RECYCLING UNITS IN KERALA Sl. No. Name, Address & Contact No. of Unit District Capacity Consent valid upto KOLLAM 1 Aapt Bags, Karalapuram , Vellimon P.O., Recycling of carry KLM 1 Kollam Kollam Bags@50 nos/day 30/04/2019 2 Ani Plastic, Mini Industrieal Estate , Muzhungodi , Thodiyoor P.O , KLM 2 Karunagappally , Kollam Kollam Lamps @ 225 Kg/Day 28/02/2019 3 Bilal Industries, Keezhchira , Myyanad P.O Recycled plastic KLM 3 Kollam Kollam Granules @ 20 kg/day 31/03/2019 4 Lulu Plastics, Mini Industrial Estate, Muzhangodi,Thodiyoor, Plastic Sheet @ 200 Kg/Day KLM 4 Karunagappally, Kollam Kollam 30/06/2018 5 Lulu Plastics, Mini Industrial Estate, Recycling of plastic @ KLM 5 Thodiyoor, Karunagappally, Kollam Kollam 200 kg/day 30/06/2018 6 M. G. M. Industries, Vemannoor , Anakkoottoor P.O , Kottarakkara , Kollam Recycled Plastic Lumps @ 1000 KLM 6 Kollam Kg/Day 31/05/2020 7 Mahadeva Industries, Mini Industrieal Estate, Kollam Recycling Of Plastic LDPE , HDPE, 31/12/2017 KLM 7 Muzhungodi. Thodiyoor P.O , Karunagapplly , Kollam PVC Conduits @ 60kg/Day 8 Nunnu Plastics , Thodiyoor , PVC products @ 1500 26/09/2018 KLM 8 Kunnathoor , Kollam Kollam Nos/day 9 Plastic container from virgin Plastotech, Paniker Kadavu , S. V. M P.O , Kozhikode plastics @ 55 KLM 9 ,Kollam. Kollam Kg/day 30/05/2018 10 Polymers Horizon, Polymers Horizon,Shed No:8,Mini Industrail Estate,Sasthamcotta P.O,Bharanikavu,Kollam-690521 Reprocessed Plastic Granules @ KLM 10 Kollam 25 Nos/Day 11/05/2019 11 Sas Plastics, Mini Industrial Estatepirvanthoor , Kadakkamom ,Kollam Recycled Plastic Lumps @ 1000 KLM 11 Kollam Kg/Day 30/09/2018 PATHANAMTHITTA 12 PTA 1 J.A. -

Amrita Kiranam April
No. 15 | Vol. 17 | April 2019 AMRITA KIRANAM a snapshot and journal of happenings @ Amrita School of Arts and Sciences, Kochi inside............ 2 International Women’s Day Celebrations Visit by Lady Officers of Indian Navy 3 Sessions on Waste Management, Women Safety and Traffic Awareness 4 Book Fair and Quiz Contest 5 Kalamritam 2019 Student’s Portfolio 6 Anuvarthan 2019 - CSI Tech Fest 7 Workshop on Deep Learning 8 Avyukta 2019 - Commerce and Management Fest 9 National Workshop on Structural Equation Modeling using AMOS 10 Animation and VFX Workshop 11 An ‘ARTSY’ Trip - Kochi Biennale 2019 12 Workshop on Linear Algebra 13 National Science Day - 2019 (Sastramritam) 14 International Conference on Travel Narratives International Women’s Day Celebrations International Women’s Day 2019 ‘Janani’ was celebrated on 6th, 7th and 8th March. Beginning with the blessing address by Swami Purnamritananda Puri and a welcome dance by Ms. Lavanya and team, the inaugural address was delivered by a renowned scientist Dr. B. Valsa, Deputy Director- Systems Reliability, Vikram Sarabhai Space Centre (VSSC) and recipient of many awards for her excellent contribution to ISRO. There was a Kathak performance by S. Anupama of 4th Semester BBA among other cultural programmes. On 7th the Dietetics Department of Amrita Institute of Medical Sciences led by Bri. Nivedita, HOD held a session on On 8th March Smt. Patil Pranjil Lahensingh, In the same function chief guest ‘Balanced and healthy diet for women’ IAS, Asst. Collector, Ernakulam was the honoured Sri. K. Jayadevan, President, which was followed by ‘Amrita Paakam’ chief guest. Smt Patil is the first visually Pookkottukavu Grama Panchayat, cooking contest by our staff and students. -

Accused Persons Arrested in Ernakulam Rural District from 15.12.2019To21.12.2019
Accused Persons arrested in Ernakulam Rural district from 15.12.2019to21.12.2019 Name of Name of the Name of the Place at Date & Arresting Court at Sl. Name of the Age & Cr. No & Sec Police father of Address of Accused which Time of Officer, which No. Accused Sex of Law Station Accused Arrested Arrest Rank & accused Designation produced 1 2 3 4 5 6 7 8 9 10 11 V. V Rasheedh, 1 Cr. 908/19, SI of Police, U/S 279,337 Munambam NIKHIL SURESH 19 M NIKATHIL HOUSE, CHERAI,Munambam PALLIPURAM18.12.2019 atIPC 11.30 Hrs Munambam P.S Station Bail V. V Rasheedh, 2 Cr. 907/19, SI of Police, U/S 279,337 Munambam SHAJI KUMARAN 41 M VETTUVELITHARA HOUSE,Munambam NEDUNGAD, NAYARAMBALAM21.12.19 at 12.30IPC Hrs Munambam P.S Station Bail Cr: 1424/19, NAMBYATHUPARA 24/19, NORTH U/S 279 IPC NORTH 3 SAYOOJ SABIYAN MBIL HOUSE, M PARAVUR & 185 MV PARAVUR VANIYAKKAD SONY ACT 15.12.19 MATHAI,SI Station Bail RAMNIVAS, OLIPPARAMBU Cr: 1425/19, RAMACHAN 27/19, KUTTANTHU NORTH 4 SREERAJ HOUSE, U/S 118(a) DRAN M RUTH PARAVUR POOSARIPADY, KP ACT SONY KIZHAKKEPRAM 15.12.19 MATHAI,SI Station Bail VADASSERRY Cr: 1425/19, JEROM ANTONY 29/19, HOUSE,PANCHAYA KUTTANTHU NORTH 5 U/S 118(a) FRANCIS JOHN M THUPADY,EDAYAK RUTH PARAVUR SONY KP ACT UNNAM 15.12.19 MATHAI,SI Station Bail NELLIPILLIPARAM Cr: 1430/19, 58/19, BU NORTH NORTH 6 ABDULLA SAIDH U/S 151 M HOUSE,MANNAM,V PARAVUR PARAVUR SONY CrPC ANIYAKKAD 17.12.19 MATHAI,SI Station Bail MANAMMEL Cr: 1431/19, BEERANKU 33/19, NORTH NORTH 7 SAJAD HOUSE,PARAPPUR U/S 151 NJU M PARAVUR PARAVUR SONY AM, KOTTUVALLY CrPC 17.12.19 MATHAI,SI -
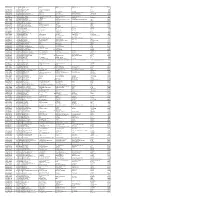
Mgl- Int 4-2015 Unpai D Shareholders List As on 30-06
FOLIO-DEMAT ID NETDIV DWNO NAME ADDRESS 1 ADDRESS 2 ADDRESS 3 City PIN 1201910100545543 45.00 15410593 DIVESH SACHDEVA T - 2638, HARDHYAN SINGH MARG FAIZ ROAD, KAROLBAGH NEW DELHI 110005 1203320007146634 270.00 15410949 MOHINDER KAUR B-162 I FLOOR FATEH NAGAR DELHI 110018 1203460000333748 516.00 15411360 SURESH BAID 91, SAINIK VIHAR PITAM PURA DELHI 110034 IN30159010007933 23.00 15411460 S.M.JAIN H.NO.895, GALI JAIN MANDIR, NAJAFGARG, NEW DELHI 110043 1204470000418754 45.00 15412114 AMIT TIWARI UPKAR COLONY HOUSE NO B-2/1 OPP BURARI GOVT SCHOOL BURARI DELHI 110084 IN30236510644395 208.00 15413996 AJAY KUMAR SHARMA H.NO.- D-10, SANJAY NAGAR, SECTOR-23, GHAZIABAD, UTTAR PRADESH 201001 1203320004195371 32.00 15412280 KANNATH SUKUMARAN NAIR 159 C BLOCK B S SHALIMAR BAGH NEW DELHI 110088 1203200000001219 225.00 15412326 SAROJ SAXENA . B-70, GALI NO.10, SASHI GARDEN NEELKANTH APARTMENT MAYUR VIHAR, PHASE - 1 DELHI 110091 IN30133017791439 1.00 15413742 NISCHAL ARORA H.NO 399 FIRST FLOOR SECTOR 20 A, CHANDIGARH 160019 IN30036021965318 45.00 15414219 KIRTI RAJ SINGH B 644 SAINIK COLONY SECTOR 49 FARIDABAD 201301 IN30177416845663 45.00 15414341 POOJA SINGHAL H NO 349 STRT MAMOORA GANV VILL MAMOORA POLICE STN SEC 58 GAUTAM BUDH NAGAR NOIDA 201307 IN30105510700089 118.00 15414529 DAYA SHANKER SHUKLA 10/175 KHALASI LINE KANPUR 208002 IN30254010005948 45.00 15413998 VINOD KUMAR SHARMA 231 MIRZAZAN DASNA GATE GHAZIABAD 201001 1206140000059951 45.00 15414540 MANOJ KUMAR SINGH 86/243 RAI PURWA KANPUR 208003 IN30001110703000 135.00 15414611 MAN MOHAN SINGH