UC San Diego UC San Diego Electronic Theses and Dissertations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lectures and Seminars, Trinity Term 2015
WEDNESDay 22 april 2015 • SUpplEMENT (2) TO NO 5092 • VOl 145 Gazette Supplement Lectures and Seminars, Trinity term 2015 Romanes Lecture 462 Experimental psychology Buddhist Studies Orthopaedics, rheumatology and COMPAS Musculoskeletal Sciences Hebrew and Jewish Studies University Administration pathology Hindu Studies and Services 462 pharmacology Museum of the History of Science Disability Lecture physiology, anatomy and Genetics islamic Studies population Health reuters institute for the Study of Humanities 462 psychiatry Journalism Foundation for law, Justice and Society TOrCH | The Oxford research Centre in Social Sciences 470 the Humanities learning institute Maison Française rothermere american institute interdisciplinary research Methods Oxford Martin School Classics Sanjaya lall Memorial Trust population ageing English language and literature anthropology and Museum Ethnography ian ramsey Centre History Saïd Business School linguistics, philology and phonetics Economics Colleges, Halls and Societies 482 Medieval and Modern languages Education Music interdisciplinary area Studies all Souls Oriental Studies international Development (Queen Balliol philosophy Elizabeth House) Green Templeton Theology and religion Oxford internet institute Keble Law lady Margaret Hall Mathematical, Physical and politics and international relations linacre Life Sciences 466 Social policy and intervention lincoln Socio-legal Studies Chemistry Magdalen Sociology Computer Science Mansfield Nuffield Earth Sciences Department for Continuing Queen’s Engineering -

Download Chapter (PDF)
The CoRoT Legacy Book c The authors, 2016 DOI: 10.1051/978-2-7598-1876-1.c031 III.1 Transit features detected by the CoRoT/Exoplanet Science Team M. Deleuil1, C. Moutou1, J. Cabrera2, S. Aigrain3, F. Bouchy1, H. Deeg4, P. Bord´e5, and the CoRoT Exoplanet team 1 Aix Marseille Universite,´ CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388, Marseille, France 2 Institute of Planetary Research, German Aerospace Center, Rutherfordstrasse 2, 12489 Berlin, Germany 3 Department of Physics, Denys Wilkinson Building Keble Road, Oxford, OX1 3RH 4 Instituto de Astrofisica de Canarias, 38205 La Laguna, Tenerife, Spain and Universidad de La Laguna, Dept. de Astrof´ısica, 38206 La Laguna, Tenerife, Spain 5 Institut d’astrophysique spatiale, Universite´ Paris-Sud 11 & CNRS (UMR 8617), Bat.ˆ 121, 91405 Orsay, France While this is reliable on a statistical point of view, individ- 1. Introduction ual targets could be misclassified (Damiani et al. this book) CoRoT has observed 26 stellar fields located in two oppo- and these numbers are mostly indicative of the overall stel- site directions for transiting planet hunting. The fields ob- lar population properties. They show however that, in a served near 6h 50m in right ascension are referred as (galac- given field, classes V and IV represent the majority of the tic) \anti-center fields”, and those near 18h 50m as \center targets. Figure III.1.2 displays how these stars classified fields”. The observing strategy consisted in staring a given as class IV and V distribute over spectral types F, G, K, star field for durations that ranged from 21 to 152 days. -

The False Positive Probability of Corot and Kepler Planetary Candidates
EPSC Abstracts Vol. 6, EPSC-DPS2011-1243, 2011 EPSC-DPS Joint Meeting 2011 c Author(s) 2011 The False Positive probability of CoRoT and Kepler planetary candidates. R.F. Díaz (1,2), J.M. Almenara (3), A. Bonomo (3), F. Bouchy (1,2), M. Deleuil (3), G. Hébrard (1,2), C. Moutou (3) and A. Santerne (3) (1) Institut d’astrophysique de Paris, FRANCE, (2) Observatoire de Haute-Provence, FRANCE, (3) Laboratoire d’Astrophysique de Marseille, FRANCE ([email protected]) Abstract tified, similarly to what is done for planet candidates detected from RV surveys, a fraction of which are in We estimate the False Positive Probability of CoRoT actuality low-mass objects in low-inclination orbits. and Kepler planetary candidates, and review critically Therefore, since the rapidly-growing number of previous results present in the literature. The ob- transiting planet candidates makes it increasingly dif- tained estimates are compared with the results from ficult to confirm each one individually by means of RV the ground-based radial velocity follow-up carried out measurements, a precise and reliable estimation of the with the HARPS and SOPHIE spectrographs for these FPP is of great importance to obtain the greatest sci- two space missions. entific return from the data acquired by CoRoT and Kepler, as well as to fully exploit the data that will be 1. Introduction obtained from future missions, like PLATO. The CoRoT and Kepler space missions are dedicated to finding transit-like events caused by extrasolar plan- 2. The False Positives ets in orbits aligned with the line of sight from Earth. -

Extracting Cosmology from High Resolution CMB Data *Focused on ACT and SO
Extracting cosmology from high resolution CMB data *focused on ACT and SO Jo Dunkley, Princeton University May 23, 2018 Jo Dunkley Cosmic Microwave Background T=2.7K ∆T/T ~0.00001 Also polarization: Rep.Two-point statistics: Prog. Phys. 81 (2018) 044901 Report on Progress TxT TxE BxB ExE Staggs, JD, Page 2018 review Figure 3. Example of recent CMB power spectra from [50–54]. Left. TT (top) and EE (bottom) data and power spectra plotted with logarithmic y axes. The TT and EE oscillations are out of phase by ∼π/2 as expected for acoustic oscillations (see section 1.4) since TT and EE trace density and velocity, respectively. The TT spectrum at low ℓ, corresponding to superhorizon scales at decoupling (see section 2.1), has post-decoupling contributions from gravitational redshifting of the photons as they pass through evolving potential wells, known as the integrated Sachs-Wolfe (ISW) effect [55, 56]. The EE spectrum peaks at higher ℓ than TT both because it lacks the ISW effect, and because the acoustic oscillation velocity gradients sourcing the polarization grow with k and thus with ℓ. The spectra are suppressed at large ℓ due to photon diffusion from smaller regions of space, also called Silk damping [57], and to geometric effects from compressing the 3d structure to 2d spectra. Right. TE with linear y axis. Since the ISW effect does not change the polarization, the negative peak at ℓ = 150 in TE confrmed that some of the largest scale features in the CMB are primordial, and not just late-time effects [58–60]. -

The Trilogy Is Complete -- Gigagalaxy Zoom Phase 3 28 September 2009
The trilogy is complete -- GigaGalaxy Zoom Phase 3 28 September 2009 "globules" and the most prominent ones have been catalogued by the astronomer Edward Emerson Barnard. The Lagoon Nebula hosts the young open stellar cluster known as NGC 6530. This is home for 50 to 100 stars and twinkles in the lower left portion of the nebula. Observations suggest that the cluster is slightly in front of the nebula itself, though still enshrouded by dust, as revealed by reddening of the starlight, an effect that occurs when small dust particles scatter light. The third image of ESO's GigaGalaxy Zoom project is an amazing vista of the Lagoon Nebula taken with the 67-million-pixel Wide Field Imager attached to the MPG/ESO 2.2-meter telescope at the La Silla Observatory in Chile. The image covers more than one and a half square degree -- an area eight times larger than that of the Full Moon -- with a total of about 370 million pixels. It is based on images acquired using three different broadband filters (B, V, R) and one narrow- band filter (H-alpha). Credit: ESO The newly released image extends across a field of view of more than one and a half square degree — an area eight times larger than that of the full Moon — and was obtained with the Wide Field Imager attached to the MPG/ESO 2.2-metre telescope at the La Silla Observatory in Chile. This 67-million-pixel camera has already created several of ESO's iconic pictures. The intriguing object depicted here — the Lagoon Nebula — is located four to five thousand light- years away towards the constellation of Sagittarius The three images of ESO’s GigaGalaxy Zoom project (the Archer). -

HATS-3B: an Inflated Hot Jupiter Transiting an F-Type Star
Draft version January 5, 2018 A Preprint typeset using LTEX style emulateapj v. 5/2/11 HATS-3b: AN INFLATED HOT JUPITER TRANSITING AN F-TYPE STAR D. Bayliss1, G. Zhou1, K. Penev2,3, G. A.´ Bakos2,3,⋆,⋆⋆, J. D. Hartman2,3, A. Jordan´ 4, L. Mancini5, M. Mohler5, V. Suc4, M. Rabus4, B. Beky´ 3, Z. Csubry2,3, L. Buchhave6, T. Henning5, N. Nikolov5, B. Csak´ 5, R. Brahm4, N. Espinoza4, R. W. Noyes3, B. Schmidt1, P. Conroy1, D. J. Wright,7,8, C. G. Tinney,7,8, B. C. Addison,7,8, P. D. Sackett,1, D. D. Sasselov3, J. Laz´ ar´ 9, I. Papp9, P. Sari´ 9 Draft version January 5, 2018 ABSTRACT We report the discovery by the HATSouth survey of HATS-3b, a transiting extrasolar planet orbiting a V=12.4 F dwarf star. HATS-3b has a period of P =3.5479d, mass of Mp =1.07 MJ, and radius of Rp =1.38 RJ. Given the radius of the planet, the brightness of the host star, and the stellar rotational 1 velocity (v sin i = 9.0kms− ), this system will make an interesting target for future observations to measure the Rossiter-McLaughlin effect and determine its spin-orbit alignment. We detail the low/medium-resolution reconnaissance spectroscopy that we are now using to deal with large numbers of transiting planet candidates produced by the HATSouth survey. We show that this important step in discovering planets produces log g and Teff parameters at a precision suitable for efficient candidate vetting, as well as efficiently identifying stellar mass eclipsing binaries with radial velocity 1 semi-amplitudes as low as 1 km s− . -

Neutrino Cosmology and Large Scale Structure
Neutrino cosmology and large scale structure Christiane Stefanie Lorenz Pembroke College and Sub-Department of Astrophysics University of Oxford A thesis submitted for the degree of Doctor of Philosophy Trinity 2019 Neutrino cosmology and large scale structure Christiane Stefanie Lorenz Pembroke College and Sub-Department of Astrophysics University of Oxford A thesis submitted for the degree of Doctor of Philosophy Trinity 2019 The topic of this thesis is neutrino cosmology and large scale structure. First, we introduce the concepts needed for the presentation in the following chapters. We describe the role that neutrinos play in particle physics and cosmology, and the current status of the field. We also explain the cosmological observations that are commonly used to measure properties of neutrino particles. Next, we present studies of the model-dependence of cosmological neutrino mass constraints. In particular, we focus on two phenomenological parameterisations of time-varying dark energy (early dark energy and barotropic dark energy) that can exhibit degeneracies with the cosmic neutrino background over extended periods of cosmic time. We show how the combination of multiple probes across cosmic time can help to distinguish between the two components. Moreover, we discuss how neutrino mass constraints can change when neutrino masses are generated late in the Universe, and how current tensions between low- and high-redshift cosmological data might be affected from this. Then we discuss whether lensing magnification and other relativistic effects that affect the galaxy distribution contain additional information about dark energy and neutrino parameters, and how much parameter constraints can be biased when these effects are neglected. -
Understanding Cosmic Acceleration: Connecting Theory and Observation
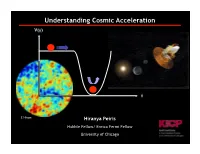
Understanding Cosmic Acceleration V(!) ! E Hivon Hiranya Peiris Hubble Fellow/ Enrico Fermi Fellow University of Chicago #OMPOSITIONOFAND+ECosmic HistoryY%VENTS$ UR/ INGTHE%CosmicVOLUTIONOFTHE5 MysteryNIVERSE presentpresent energy energy Y density "7totTOT = 1(k=0)K density DAR RADIATION KENER dark energy YDENSIT DARK G (73%) DARKMATTER Y G ENERGY dark matter DARK MA(23.6%)TTER TIONOFENER WHITEWELLUNDERSTOOD DARKNESSPROPORTIONALTOPOORUNDERSTANDING BARYONS BARbaryonsYONS AC (4.4%) FR !42 !33 !22 !16 !12 Fractional Energy Density 10 s 10 s 10 s 10 s 10 s 1 sec 380 kyr 14 Gyr ~1015 GeV SCALEFACTimeTOR ~1 MeV ~0.2 MeV 4IME TS TS TS TS TS TSEC TKYR T'YR Y Y Planck GUT Y T=100 TeV nucleosynthesis Y IES TION TS EOUT DIAL ORS TIONS G TION TION Z T Energy THESIS symmetry (ILC XA 100) MA EN EE WNOF ESTHESIS V IMOR GENERATEOBSERVABLE IT OR ELER ALTHEOR TIONS EF SIGNATURESINTHE#-" EAKSYMMETR EIONIZA INOFR Y% OMBINA R E6 EAKDO #X ONASYMMETR SIC W '54SYMMETR IMELINEOF EFFWR Y Y EC TUR O NUCLEOSYN ), * +E R 4 PLANCKENER Generation BR TR TURBA UC PH Cosmic Microwave NEUTR OUSTICOSCILLA BAR TIONOFPR ER A AC STR of primordial ELEC non-linear growth of P 44 LIMITOFACC Background Emitted perturbations perturbations: GENER ES carries signature of signature on CMB TUR GENERATIONOFGRAVITYWAVES INITIALDENSITYPERTURBATIONS acoustic#-"%MITT oscillationsED NON LINEARSTR andUCTUR EIMPARTS #!0-!0OBSERVES#-" ANDINITIALDENSITYPERTURBATIONS GROWIMPARTINGFLUCTUATIONS CARIESSIGNATUREOFACOUSTIC SIGNATUREON#-"THROUGH *throughEFFWRITESUPANDGR weakADUATES WHICHSEEDSTRUCTUREFORMATION -

Search for Wide Substellar Companions to Young Nearby Stars with the VISTA Hemisphere Survey
Highlights on Spanish Astrophysics X, Proceedings of the XIII Scientific Meeting of the Spanish Astronomical Society held on July 16 – 20, 2018, in Salamanca, Spain. B. Montesinos, A. Asensio Ramos, F. Buitrago, R. Schödel, E. Villaver, S. Pérez-Hoyos, I. Ordóñez-Etxeberria (eds.), 2019 Search for wide substellar companions to young nearby stars with the VISTA Hemisphere Survey. P. Chinchilla1;2, V.J.S. B´ejar1;2, N. Lodieu1;2, M.R. Zapatero Osorio3, B. Gauza4, R. Rebolo1;2;5, and A. P´erezGarrido6 1 Instituto de Astrof´ısicade Canarias (IAC), c/V´ıaL´acteaS/N, 38200 La Laguna, Tenerife, Spain 2 Dpto. de Astrof´ısica,Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain 3 Centro de Astrobiolog´ıa(CSIC-INTA), Ctra. de Ajalvir km 4, 28850 Torrej´onde Ardoz, Madrid, Spain 4 Dpto. de Astronom´ıa,Universidad de Chile, Camino el Observatorio 1515, Casilla 36-D, Las Condes, Santiago, Chile 5 Consejo Superior de Investigaciones Cient´ıficas(CSIC), Spain 6 Dpto. de F´ısicaAplicada, Universidad Polit´ecnicade Cartagena, 30202 Cartagena, Murcia, Spain Abstract We have performed a search for substellar objects as common proper motion companions to young nearby stars (including members of the Young Moving Groups AB Doradus, TW Hydrae, Tucana-Horologium and Beta Pictoris, and the Upper Scorpius young association) up to separations of 50,000 AU, using the VISTA Hemisphere Survey and 2MASS astro- metric and photometric data. We have found tens of candidates with spectral types from M to L, and estimated masses from low-mass stars to the deuterium-burning limit mass. -

From Dark Matter to Galaxies with Convolutional Networks
From Dark Matter to Galaxies with Convolutional Networks Xinyue Zhang*, Yanfang Wang*, Wei Zhang*, Siyu He Yueqiu Sun*∗ Department of Physics, Carnegie Mellon University Center for Data Science, New York University Center for Computational Astrophysics, Flatiron Institute xz2139,yw1007,wz1218,[email protected] [email protected] Gabriella Contardo, Francisco Shirley Ho Villaescusa-Navarro Center for Computational Astrophysics, Flatiron Institute Center for Computational Astrophysics, Flatiron Institute Department of Astrophysical Sciences, Princeton gcontardo,[email protected] University Department of Physics, Carnegie Mellon University [email protected] ABSTRACT 1 INTRODUCTION Cosmological surveys aim at answering fundamental questions Cosmology focuses on studying the origin and evolution of our about our Universe, including the nature of dark matter or the rea- Universe, from the Big Bang to today and its future. One of the holy son of unexpected accelerated expansion of the Universe. In order grails of cosmology is to understand and define the physical rules to answer these questions, two important ingredients are needed: and parameters that led to our actual Universe. Astronomers survey 1) data from observations and 2) a theoretical model that allows fast large volumes of the Universe [10, 12, 17, 32] and employ a large comparison between observation and theory. Most of the cosmolog- ensemble of computer simulations to compare with the observed ical surveys observe galaxies, which are very difficult to model theo- data in order to extract the full information of our own Universe. retically due to the complicated physics involved in their formation The constant improvement of computational power has allowed and evolution; modeling realistic galaxies over cosmological vol- cosmologists to pursue elucidating the fundamental parameters umes requires running computationally expensive hydrodynamic and laws of the Universe by relying on simulations as their theory simulations that can cost millions of CPU hours. -

Dark Matter Search with the Newsdm Experiment Using Machine Learning Techniques
UNIVERSITÀ DEGLI STUDI DI NAPOLI “FEDERICO II” Scuola Politecnica e delle Scienze di Base Area Didattica di Scienze Matematiche Fisiche e Naturali Dipartimento di Fisica “Ettore Pancini” Laurea Magistrale in Fisica Dark Matter search with the NEWSdm experiment using machine learning techniques Relatori: Candidato: Prof. Giovanni De Lellis Chiara Errico Dott.ssa Antonia Di Crescenzo Matricola N94/457 Dott. Andrey Alexandrov Anno Accademico 2018/2019 Acting with love brings huge happening · Contents Introduction1 1 Dark matter: first evidences and detection3 1.1 First evidences of dark matter.................3 1.2 WIMPs..............................8 1.3 Search for dark matter...................... 11 1.4 Direct detection.......................... 13 1.5 Detectors for direct search.................... 15 1.5.1 Bolometers........................ 16 1.5.2 Liquid noble-gas detector................. 17 1.5.3 Scintillator......................... 18 1.6 Direct detection experiment general result........... 20 1.7 Directionality........................... 21 1.7.1 Nuclear Emulsion..................... 23 2 The NEWSdm experiment 25 2.1 Nano Imaging Trackers...................... 25 2.2 Layout of the NEWSdm detector................ 28 2.2.1 Technical test....................... 29 2.3 Expected background....................... 30 2.3.1 External background................... 31 2.3.2 Intrinsic background................... 34 2.3.3 Instrumental background................. 35 2.4 Optical microscope........................ 35 2.4.1 Super-resolution microscope for dark matter search.. 38 2.5 Candidate Selection........................ 40 2.6 Candidate Validation....................... 42 iii Contents iv 3 Reconstruction of nanometric tracks 47 3.1 Scanning process......................... 47 3.2 Analysis of NIT exposed to Carbon ions............ 49 3.3 Shape analysis........................... 50 3.4 Plasmon analysis......................... 51 3.4.1 Accuracy.......................... 52 3.4.2 Npeaks.......................... -

1St Edition of Brown Physics Imagine, 2017-2018
A note from the chair... "Fellow Travelers" Ladd Observatory.......................11 Sci-Toons....................................12 Faculty News.................. 15-16, 23 At-A-Glance................................18 s the current academic year draws to an end, I’m happy to report that the Physics Department has had Newton's Apple Tree................. 23 an exciting and productive year. At this year's Commencement, the department awarded thirty five "Untagling the Fabric of the undergraduate degrees (ScB and AB), twenty two Master’s degrees, and ten Ph.D. degrees. It is always Agratifying for me to congratulate our graduates and meet their families at the graduation ceremony. This Universe," Professor Jim Gates..26 Alumni News............................. 27 year, the University also awarded my colleague, Professor J. Michael Kosterlitz, an honorary degree for his Events this year......................... 28 achievement in the research of low-dimensional phase transitions. Well deserved, Michael! Remembering Charles Elbaum, Our faculty and students continue to generate cutting-edge scholarships. Some of their exciting Professor Emeritus.................... 29 research are highlighted in this magazine and have been published in high impact journals. I encourage you to learn about these and future works by watching the department YouTube channel or reading faculty’s original publications. Because of their excellent work, many of our undergraduate and graduate students have received students prestigious awards both from Brown and externally. As Chair, I feel proud every time I hear good news from our On the cover: PhD student Shayan Lame students, ranging from receiving the NSF Graduate Fellowship to a successful defense of thier senior thesis or a Class of 2018.............................