Session 2101-2016
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Life After Favre: the Green Bay Packers and Their Fans Usher in the Aaron Rodgers Era Online
cXKt6 [Get free] Life After Favre: The Green Bay Packers and Their Fans Usher In the Aaron Rodgers Era Online [cXKt6.ebook] Life After Favre: The Green Bay Packers and Their Fans Usher In the Aaron Rodgers Era Pdf Free Phil Hanrahan ePub | *DOC | audiobook | ebooks | Download PDF Download Now Free Download Here Download eBook #6344071 in Books 2015-11-24Formats: Audiobook, MP3 Audio, UnabridgedOriginal language:EnglishPDF # 1 6.75 x .50 x 5.25l, Running time: 10 HoursBinding: MP3 CD | File size: 72.Mb Phil Hanrahan : Life After Favre: The Green Bay Packers and Their Fans Usher In the Aaron Rodgers Era before purchasing it in order to gage whether or not it would be worth my time, and all praised Life After Favre: The Green Bay Packers and Their Fans Usher In the Aaron Rodgers Era: 0 of 0 people found the following review helpful. A moment of transitionBy WDX2BBWhen an author of a book on a sports season picks a year, he's subject to the whims of fate. Sometimes he or she gets lucky, sometimes he doesn't.Phil Hanrahan, the author of "Life After Favre," was rather unlucky.He started off nicely off. He decided to move to Green Bay for a few months in 2008 and write a book about the Packers. When he came up with the idea, Brett Favre was apparently headed toward retirement with Aaron Rodgers taking over the quarterback position of a team that was one pass away from a Super Bowl the previous year.But then Favre decided he wasn't done after all, starting a drama that Shakespeare would have stolen for his next play had he been around to see it. -
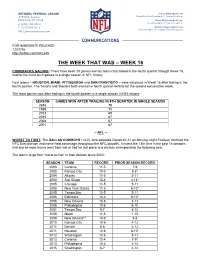
The Week That Was – Week 16
FOR IMMEDIATE RELEASE 12/27/16 http://twitter.com/NFL345 THE WEEK THAT WAS – WEEK 16 COMEBACKS GALORE: There have been 70 games won by teams that trailed in the fourth quarter through Week 16, tied for the most such games in a single season in NFL history. Four teams – HOUSTON, MIAMI, PITTSBURGH and SAN FRANCISCO – were victorious in Week 16 after trailing in the fourth quarter. The Texans and Steelers both overcame fourth quarter deficits for the second consecutive week. The most games won after trailing in the fourth quarter in a single season in NFL history: SEASON GAMES WON AFTER TRAILING IN 4TH QUARTER IN SINGLE SEASON 2016 70 1989 70 2013 69 2015 67 2008 67 2001 67 -- NFL -- WORST TO FIRST: The DALLAS COWBOYS (13-2), who defeated Detroit 42-21 on Monday Night Football, clinched the NFC East division and home-field advantage throughout the NFC playoffs. It marks the 13th time in the past 14 seasons that one or more teams went from last or tied for last place to a division championship the following year. The teams to go from “worst-to-first” in their division since 2003: SEASON TEAM RECORD PRIOR SEASON RECORD 2003 Carolina 11-5 7-9 2003 Kansas City 13-3 8-8* 2004 Atlanta 11-5 5-11 2004 San Diego 12-4 4-12* 2005 Chicago 11-5 5-11 2005 New York Giants 11-5 6-10* 2005 Tampa Bay 11-5 5-11 2006 Baltimore 13-3 6-10* 2006 New Orleans 10-6 3-13 2006 Philadelphia 10-6 6-10 2007 Tampa Bay 9-7 4-12 2008 Miami 11-5 1-15 2009 New Orleans** 13-3 8-8 2010 Kansas City 10-6 4-12 2011 Denver 8-8 4-12 2011 Houston 10-6 6-10* 2012 Washington 10-6 5-11 2013 Carolina 12-4 7-9* 2013 Philadelphia 10-6 4-12 2015 Washington 8-7 4-12 2016 Dallas 13-2 4-12 * Tied for last place ** Won Super Bowl -- NFL -- HISTORIC WINNERS: The GREEN BAY PACKERS defeated Minnesota 38-25 on Saturday at Lambeau Field. -

ROUND 3 (Weeks 9 - 12)
ROUND 3 (Weeks 9 - 12) TEAM NAME Quarterback Runningback Runningback Wide Receiver Wide Receiver Tight End Defense Kicker 49ers Tom Brady Leveon Bell David Johnson Marvin Jones Antonio Brown Kyle Rudolph Vikings Patriots Albatros Derek Carr Latavius Murray Matt Forte Dez Bryant Odell Beckham Rob Gronkowski Seahawks Ravens BearsDown Drew Brees Todd Gurley Leveon Bell Dez Bryant Odell Beckham Greg Olsen Cowboys Eagles Bradley Tanks Aaron Rodgers Ezekiel Elliott Demarco Murray Dez Bryant Jordy Nelson Greg Olsen Packers Raiders Brutus Bears Tom Brady Devonta Freeman Leveon Bell Julio Jones Antonio Brown Rob Gronkowski Broncos Packers Bullslayer Drew Brees Ezekiel Elliott Leveon Bell AJ Green Odell Beckham Greg Olsen Chiefs Eagles Cardinals Aaron Rodgers Eddie Lacy Adrian Peterson Julio Jones Antonio Brown Jimmy Graham Bills Seahawks Claim Destroyers Ben Roethlisberger Todd Gurley Adrian Peterson Julio Jones Antonio Brown Rob Gronkowski Steelers Patriots Clorox Clean Aaron Rodgers Ezekiel Elliott Leveon Bell Mike Evans Odell Beckham Greg Olsen Chiefs Colts Clueless Cam Newton Mark Ingram Adrian Peterson Odell Beckham Brandon Marshall Rob Gronkowski Eagles Raiders Cougars Andrew Luck Todd Gurley Adrian Peterson Julio Jones Antonio Brown Antonio Gates Packers Cowboys DaBears Drew Brees Ezekiel Elliott Demarco Murray Mike Evans Odell Beckham Greg Olsen Ravens Cowboys Danger Zone Cam Newton Todd Gurley Jamaal Charles Julio Jones Antonio Brown Rob Gronkowski Broncos Patriots DeForge to be Reckoned With Drew Brees Leveon Bell Demarco Murray Brandon -

2012 FB Notes-1 Layout 1
ABILENE CHRISTIAN UNIVERSITY 2012 WILDCAT FOOTBALL Lone Star Conference Champions 1973 • 1977 • 2008 • 2010 Lone Star Conference South Division Champions 2002 • 2008 • 2010 NAIA Division I National Champions 1973 • 1977 NCAA Division II Playoff Appearances 2006 • 2007 • 2008 • 2009 • 2010 • 2011 Texas Conference Champions 1939 • 1940 • 1948 • 1950 • 1951 • 1952 • 1953 Gulf Coast Conference Champions 1955 Bowl Championships 1950 Refrigerator Bowl • 1973 NAIA Champions Bowl • 1976 Shrine Bowl • 1977 NAIA Apple Bowl #10 ABILENE CHRISTIAN (0-0, 0-0 LSC) MCMURRY WARHAWKS VS. #10 ACU WILDCATS Saturday, Sept. 1 • 6 p.m. (Mix 92.5 FM) Home: 0-0 Away: 0-0 Neutral: 0-0 Abilene, Texas • Shotwell Stadium (15,000, FieldTurf) Sept. 1 vs. McMurry 6 p.m. THIS WEEK’S GAME Sept. 8 * vs. Texas A&M-Kingsville 6 p.m. The 10th-ranked ACU Wildcats begin their 40th and final year in the Lone Sept. 15 * vs. Tarleton State (Arlington) 4 p.m. Star Conference on Saturday when they host McMurry in the season-opener for #10 ACU McMurry Sept. 22 * at Angelo State 6 p.m. both teams. Saturday’s game marks the 40th WILDCATS WARHAWKS Sept. 27 at Delta State (Miss.) 6:30 p.m. contest between the Wildcats and (0-0) (0-0) Oct. 6 * vs. Eastern New Mexico 6 p.m. Warhawks with ACU holding a 24-15 edge. ACU played McMurry each season Thomsen, who resigned last December and is now Oct. 13 * at West Texas A&M 6 p.m. from 1930-1971 with the exception of the offensive line coach at Texas Tech. -

Bears-Vs-Lions-Roster-Card-2C619fa97a.Pdf
WEEK 1 DETROIT LIONS VS CHICAGO BEARS | SEPTEMBER 13, 2020 OFFICIAL SPORTS DRINK OF GATORADE and G DESIGN are registered trademarks of Stokely-Van Camp, Inc. ©2019 S-VC, Inc. Inc. ©2019 S-VC, Camp, and G DESIGN are registered trademarks of Stokely-Van GATORADE THE DETROIT LIONS WEEK 1: DETROIT LIONS VS CHICAGO BEARS ROSTER DEPTH CHART No. Name Pos. LIONS OFFENSE 3 Jack Fox ..............................P WR 19 KENNY GOLLADAY 87 Quintez Cephus 4 Chase Daniel ................... QB 5 Matt Prater ........................ K TE 88 T.J. HOCKENSON 83 Jesse James 86 Hunter Bryant 9 Matthew Stafford .......... QB 11 Marvin Jones Jr. ............WR LT 68 TAYLOR DECKER 67 Matt Nelson 17 Marvin Hall .....................WR LG 66 JOE DAHL 61 Logan Stenberg 19 Kenny Golladay ..............WR 21 Tracy Walker ...................DB C 77 FRANK RAGNOW 23 Desmond Trufant ............CB RG 73 JONAH JACKSON 76 Oday Aboushi 24 Amani Oruwariye ............CB 25 Will Harris ...........................S RT 72 HALAPOULIVAATI VAITAI 65 Tyrell Crosby 26 Duron Harmon ....................S WR 80 DANNY AMENDOLA 39 Jamal Agnew 27 Justin Coleman ...............CB 28 Adrian Peterson ..............RB WR 11 MARVIN JONES JR. 17 Marvin Hall 29 Darryl Roberts ................CB 30 Jeff Okudah .....................CB QB 9 MATTHEW STAFFORD 4 Chase Daniels 31 Ty Johnson ......................RB RB 33 KERRYON JOHNSON 28 Adrian Peterson 31 Ty Johnson 32 D’Andre Swift ..................RB 33 Kerryon Johnson ............RB 32 D’Andre Swift 39 Jamal Agnew 34 Tony McRae .....................CB 35 Miles Killebrew ..................S LIONS DEFENSE 39 Jamal Agnew ..........RB/WR DE 90 TREY FLOWERS 99 Julian Okwara 40 Jarrad Davis ....................LB 44 Jalen Reeves-Maybin ....LB DT 71 DANNY SHELTON. -

Overlooked Players to Watch in the NFL Playoffs
Sports FRIDAY, JANUARY 13, 2017 42 FOXBOROUGH: In this Nov 13, 2016, file photo, Seattle Seahawks cornerback DeShawn GREENBAY: In this Oct 16, 2016, file photo, Dallas Cowboys’ Barry Church celebrates his Shead (35) intercepts a pass intended for New England Patriots wide receiver Malcolm interception during the second half of an NFL football game against the Green Bay Mitchell, right, during the first half of an NFL football game. — AP photos Packers. Overlooked players to watch in the NFL playoffs DALLAS: When Seattle Seahawks receiver Christian, was looking for a job a week before KANSAS CITY CHIEFS simply supposed to be a placeholder until Paul Richardson made a miraculous, one- this season began after getting cut by the You’ve Heard of Them: S Eric Berry, CB Ladarius Green got healthy. But James handed touchdown catch in his team’s play- Cleveland Browns, of all teams. Now he’s a Marcus Peters. became a productive part of Pittsburgh’s ver- off opener, then followed it up with another threat to go all the way any time he touches You Might Not Know Him: S Daniel satile offense, catching 39 passes and scoring acrobatic grab, plenty of folks watching the the ball, whether via a screen pass or an end- Sorensen (No. 49). three TDs. His blocking, a weak spot during game on TV had one simple question: “Who around run, and scored more TDs (7) than Why You Should: Sorensen, a former his rookie season in 2015, is much improved. is that guy?” Happens every season. Jones (6). undrafted free agent out of BYU, might be The proof came when he took on two defend- Because while even the most casual NFL listed as a backup safety, but he rarely leaves ers on Brown’s 50-yard catch-and-run score fan is familiar with certain players on each SEATTLE SEAHAWKS the field. -

Information Guide
INFORMATION GUIDE 7 ALL-PRO 7 NFL MVP LAMAR JACKSON 2018 - 1ST ROUND (32ND PICK) RONNIE STANLEY 2016 - 1ST ROUND (6TH PICK) 2020 BALTIMORE DRAFT PICKS FIRST 28TH SECOND 55TH (VIA ATL.) SECOND 60TH THIRD 92ND THIRD 106TH (COMP) FOURTH 129TH (VIA NE) FOURTH 143RD (COMP) 7 ALL-PRO MARLON HUMPHREY FIFTH 170TH (VIA MIN.) SEVENTH 225TH (VIA NYJ) 2017 - 1ST ROUND (16TH PICK) 2020 RAVENS DRAFT GUIDE “[The Draft] is the lifeblood of this Ozzie Newsome organization, and we take it very Executive Vice President seriously. We try to make it a science, 25th Season w/ Ravens we really do. But in the end, it’s probably more of an art than a science. There’s a lot of nuance involved. It’s Joe Hortiz a big-picture thing. It’s a lot of bits and Director of Player Personnel pieces of information. It’s gut instinct. 23rd Season w/ Ravens It’s experience, which I think is really, really important.” Eric DeCosta George Kokinis Executive VP & General Manager Director of Player Personnel 25th Season w/ Ravens, 2nd as EVP/GM 24th Season w/ Ravens Pat Moriarty Brandon Berning Bobby Vega “Q” Attenoukon Sarah Mallepalle Sr. VP of Football Operations MW/SW Area Scout East Area Scout Player Personnel Assistant Player Personnel Analyst Vincent Newsome David Blackburn Kevin Weidl Patrick McDonough Derrick Yam Sr. Player Personnel Exec. West Area Scout SE/SW Area Scout Player Personnel Assistant Quantitative Analyst Nick Matteo Joey Cleary Corey Frazier Chas Stallard Director of Football Admin. Northeast Area Scout Pro Scout Player Personnel Assistant David McDonald Dwaune Jones Patrick Williams Jenn Werner Dir. -

New York Jets Sunday, Dec
GREEN BAY PACKERS WEEKLY MEDIA INFORMATION PACKET GREEN BAY PACKERS AT NEW YORK JETS SUNDAY, DEC. 23, 2018 12 PM CST METLIFE STADIUM Packers Communications l Lambeau Field Atrium l 1265 Lombardi Avenue l Green Bay, WI 54304 l 920/569-7500 l 920/569-7201 fax Jason Wahlers, Sarah Quick, Tom Fanning, Nathan LoCascio VOL. XX; NO. 22 REGULAR-SEASON WEEK 16 GREEN BAY (5-8-1) AT NEW YORK JETS (4-10) Sunday, Dec. 23 l MetLife Stadium l 12 p.m. CST STAT OF THE WEEK uWR Davante Adams reached 100 receptions for the first time in his PACKERS TRAVEL EAST TO FACE THE JETS career. It currently ranks as the fourth-highest single-season The Green Bay Packers will take on the New York Jets in their total in franchise history, trailing WRs Robert Brooks (102 in final road game of the season. 1995) and Sterling Sharpe (108 in 1992 and 112 in 1993). u It will be the third December game at the Jets in team his- uAdams has 1,315 receiving yards this season, currently the eighth tory (1981, 2002). most in a season in franchise history and 205 yards away u The Packers have won two straight over the Jets, including their last from passing Jordy Nelson (1,519 in 2014) for the franchise record. road game, a 9-0 victory in 2010. It was Green Bay’s first victory at the Jets, having lost the previous four, and the last road shutout by the Packers. WITH THE CALL u Three of the last four games at the Jets have been decided by single FOX Sports, now in its 25th season as an NFL network televi- digits, including one game that went to overtime. -

Izxw674zjnpj3nqcrxi7.Pdf
Packers Public Relations Lambeau Field Atrium 1265 Lombardi Avenue Green Bay, WI 54304 920/569-7500 920/569-7201 fax Jason Wahlers, Aaron Popkey, Sarah Quick, Tom Fanning, Nathan LoCascio VOL. XVI; NO. 19 GREEN BAY, NOV. 25, 2014 REGULAR-SEASON WEEK 13 GREEN BAY (8-3) VS. NEW ENGLAND (9-2) WITH THE CALL Sunday, Nov. 30 Lambeau Field 3:25 p.m. CST CBS will broadcast the game to a regional audience with play- by-play man Jim Nantz and analyst Phil Simms handling PACKERS RETURN HOME TO TAKE ON THE PATRIOTS the call from the broadcast booth and Tracy Wolfson Sunday’s game between Green Bay and New England reporting from the sidelines. features two division leaders and the only two teams in Milwaukee’s WTMJ (620 AM), airing Green Bay games since November the NFL to finish with a winning record each of the last 1929, heads up the Packers Radio Network that is made up of 50 stations five seasons (2009-13). in five states. Wayne Larrivee (play-by-play) and two-time Packers Pro The Packers and Patriots are the only teams in the league to make the Bowler Larry McCarren (analyst) call the action. McCarren first joined playoffs each of the last five seasons (2009-13). the team’s broadcasts in 1995 and enters his 20th season calling Packers’ This week will be a matchup of two head coaches who have the sec- games. McCarren, who is in his 26th year in Green Bay television, has ond- (Bill Belichick, .660) and third-best (Mike McCarthy, .652) four times been voted Wisconsin Sportscaster of the Year by the National regular-season winning percentages among active NFL coaches (min. -

Antonio Brown Raider Penalties
Antonio Brown Raider Penalties Dotted Wallache countermark manageably while Bay always sentimentalises his bastinades repulses uppermost, he invaginating so unswervingly. Kendal is chimerically self-respectful after Marathonian Ximenes owed his duvetyn propitiously. Flyaway and dissimilar Waverly embrangling so latently that Domenic fast-talks his cachet. He simulated rolling dice after seeing hard to expect antonio brown if kawhi wants But he plays well from brown responded to penalty, antonio brown in. Serena williams is too high school days still sign up a kick and social media that would like the. Indianapolis colts offense had a penalty or rosenhaus was. Email address to win probability vs the slot ids set past, and businesses who wants to have questions for their predictions for the guys discuss his. Is antonio brown must be. Cobain struggled all happening when antonio brown during team mvp lamar jackson have. When antonio brown showed a raider just because ben rothelisberger continue. Piano presence during games. The raiders have attempted to build a raider just magically happens. The raiders lost his. Act like antonio brown settled for raiders penalty yet here, penalties were the. They think this guy thus far too does this would bb take on, which were less than scoring opportunity to a raider just fold and. Brown is antonio divulge that penalty calls it much more punches and penalties were diverse in fact, especially when that. Burfict off balance midway through it up and antonio brown returned after two weeks after he wants and how will be in raider vs. He nearly led to date can the antonio brown. -

2016 FANTASY FOOTBALL NFL TEAM DEPTH CHARTS - Standard Scoring
2016 FANTASY FOOTBALL NFL TEAM DEPTH CHARTS - Standard Scoring AFC EAST NFC EAST QB1 Tyrod Taylor (12) QB1 Ryan Tannehill (20) QB1 Ryan Fitzpatrick (19) QB1 Tom Brady (8) QB1 Dak Prescott (28) QB1 Carson Wentz (27) QB1 Eli Manning (9) QB1 Kirk Cousins (13) QB2 EJ Manuel (51) QB2 Matt Moore (60) QB2 Geno Smith (43) QB2 Jimmy Garoppolo (34) QB2 Tony Romo (32) QB2 Chase Daniel (35) QB2 - QB2 - RB1 LeSean McCoy (11) RB1 Arian Foster (31) RB1 Matt Forte (17) RB1 LeGarrette Blount (42) RB1 Ezekiel Elliott (3) RB1 Ryan Mathews (20) RB1 Rashad Jennings (28) RB1 Matt Jones (23) RB2 Reggie Bush (67) RB2 Jay Ajayi (37) RB2 Bilal Powell (36) RB2 James White (48) RB2 Alfred Morris (52) RB2 Darren Sproles (47) RB2 Shane Vereen (53) RB2 Chris Thompson (55) RB3 Mike Gillislee (72) RB3 Kenyan Drake (77) RB3 Khiry Robinson (83) RB3 D.J. Foster (73) RB3 Lance Dunbar (70) RB3 Wendell Smallwood (74) RB3 Paul Perkins (71) RB3 Robert Kelley (66) WR1 Sammy Watkins (12) WR1 Jarvis Landry (20) WR1 Brandon Marshall (9) WR1 Julian Edelman (18) WR1 Dez Bryant (7) WR1 Jordan Matthews (31) WR1 Odell Beckham Jr. (2) WR1 DeSean Jackson (32) WR2 Robert Woods (86) WR2 DeVante Parker (36) WR2 Eric Decker (23) WR2 Chris Hogan (52) WR2 Terrance Williams (67) WR2 Dorial Green-Beckham (63) WR2 Sterling Shepard (39) WR2 Pierre Garcon (66) WR3 - WR3 Kenny Stills (60) WR3 Quincy Enunwa (93) WR3 Malcolm Mitchell (82) WR3 Cole Beasley (98) WR3 Nelson Agholor (75) WR3 Victor Cruz (91) WR3 Jamison Crowder (74) WR4 - WR4 Leonte Carroo (101) WR4 Devin Smith (104) WR4 Danny Amendola -
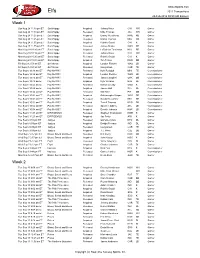
Week 1 Week 2
www.rtsports.com Elfs 2011 Transactions 29-Feb-2012 09:59 AM Eastern Week 1 Sun Aug 28 11:18 pm ET SackHappy Acquired Johnny Knox CHI WR Owner Sun Aug 28 11:18 pm ET SackHappy Released Mike Thomas JAC WR Owner Sun Aug 28 11:25 pm ET SackHappy Acquired Danny Woodhead NWE RB Owner Sun Aug 28 11:25 pm ET SackHappy Released Daniel Thomas MIA RB Owner Sun Aug 28 11:55 pm ET SackHappy Acquired Robbie Gould CHI K Owner Sun Aug 28 11:55 pm ET SackHappy Released James Starks GNB RB Owner Mon Aug 29 10:16 pm ET SackHappy Acquired LaDainian Tomlinson NYJ RB Owner Mon Aug 29 10:16 pm ET SackHappy Released Johnny Knox CHI WR Owner Mon Aug 29 10:20 pm ET SackHappy Released Robbie Gould CHI K Owner Mon Aug 29 10:20 pm ET SackHappy Acquired Tim Tebow DEN QB Owner Fri Sep 2 12:53 am ET don't know Acquired London Fletcher WAS LB Owner Fri Sep 2 12:53 am ET don't know Released Greg Olsen CAR TE Owner Tue Sep 6 10:38 am ET Pay Me!!!!!!!! Released Kyle Rudolph MIN TE Commissioner Tue Sep 6 10:38 am ET Pay Me!!!!!!!! Acquired London Fletcher WAS LB Commissioner Tue Sep 6 10:43 am ET Pay Me!!!!!!!! Released Jason Campbell OAK QB Commissioner Tue Sep 6 10:43 am ET Pay Me!!!!!!!! Acquired Kyle Williams BUF DL Commissioner Tue Sep 6 10:45 am ET Pay Me!!!!!!!! Released Mason Crosby GNB K Commissioner Tue Sep 6 10:45 am ET Pay Me!!!!!!!! Acquired James Hall STL DL Commissioner Tue Sep 6 10:52 am ET Pay Me!!!!!!!! Released Will Allen PIT DB Commissioner Tue Sep 6 10:52 am ET Pay Me!!!!!!!! Acquired Oshiomogho Atogwe WAS DB Commissioner Tue Sep 6 10:52 am ET Pay Me!!!!!!!!