DOCSLIB.ORG

Orbit Calculation and Re-Entry Control of Vorsat Satellite

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Orbit Calculation and Re-Entry Control of Vorsat Satellite FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO Orbit Calculation and Re-Entry Control of VORSat Satellite Cristiana Monteiro Silva Ramos PROVISIONAL VERSION Master in Electrical and Computers Engineering Supervisor: Sérgio Reis Cunha (PhD) June 2011 Resumo Desde o lançamento do primeiro satélite artificial para o espaço, Sputnik, mais de 30 000 satélites foram desenvolvidos e foram lançados posteriormente. No entanto, por mais autonomia que o satélite possa alcançar, nenhum satélite construido pelo Homem teria valor se não fosse possível localiza-lo e comunicar com ele. Os olhos humanos foram os primeiros recursos de que os seres humanos dispuseram para observar o Universo. O telescópio surgiu depois e foi durante séculos o único instrumento de exploração do Espaço. Hoje em dia, é possível localizar e seguir o trajecto que o satélite faz no espaço através de programas computacionais que localizam o satélite num dado instante e fazem a previsão do cálculo da órbita. Esta dissertação descreve o desenvolvimento de um sistema de navegação enquadrado no caso de estudo do satélite VORSat. O VORSat é um programa de satélite em desenvolvido na Faculdade de Engenharia da Universidade do Porto (FEUP), Potugal. Este projecto refere-se à construção de um CubeSat, de nome GAMA-Sat, e à reentrada de uma cápsula na Terra (ERC). Os objectivos consistem em determinar os parâmetros que descrevem uma órbita num dado instante (elementos de Kepler) e em calcular as posições futuras do satélite através de observações iterativas, minimizando o erro associado a cada observação. Também se pretende controlar, através de variações do termo de arrastamento, o local de reentrada. Dois métodos estimativos foram abordados: Filtro de Kalman e Mínimos quadrados. Estes foram adaptados ao caso de estudo por forma a avaliar a melhor performance num sistema não-linear tendo em consideração três aspectos: (1) O consumo de bateria no microcontrolador; (2) A capacidade de espaço limitada no microcontrolador; e (3) A precisão das medidas. Apesar deste projecto estar a ser desenvolvido no âmbito do VORSat, utilizou-se dois satélites que se encontram em órbita para validação de resultados. Optou-se pelo PoSAT e o International Space Station (ISS) por ambos se encontrarem em órbita baixa (LEO), terem uma órbita estável e ainda permanecem em órbita passado tantos anos, o que não é usual em satélites de órbita baixa. i ii Abstract Since the first artificial satellite was launched into space, Sputnik, more than 30,000 satellites have been developed and followed him. Regardless of the level of autonomy that the satellites can reach, any man-made spacecraft would have no value if it was unable to locate it and communicate with it. Human eyes were the first resources that humans had to observe the universe. The telescope came later and was used for centuries for space exploration. Nowadays, it is possible to locate and follow satellites in space through computer programs that compute the location of the satellites at any time and predict their orbits. This thesis describes the development of a navigation system that was carried out having in mind a specific case study, VORSat. VORSat is a small satellite program being developed at the Faculty of Engineering of the University of Porto (FEUP), Potugal. This project regards both the development of a CubeSat (named GAMA-Sat) and an Earth Reentry Capsule (ERC). The objective to determine the parameters that describe an orbit at a given moment (Kepler elements) and, through iterative observations to calculate the future positions of the satellite. Er- rors associated with each observation were to be minimized. Another objective was control the location of de-orbiting, through variations of the drag term. Two methods were discussed for the estimator technique: Kalman Filter and Least Squares. They were adapted to the case study in order to evaluate the best performance in a nonlinear system taking into account three aspects: (1) Battery consumption in the microcontroller; (2) limited storage space in the microcontroller; and (3) the accuracy of the measurements. Within the scope of this thesis, it was used two satellites: International Space Station (ISS) and PoSAT, in order to obtain results of the developed algorithm. The choice felt upon these two satellites due the fact that both of them are in LEO orbit, have a stable orbit and remain in orbit for many years. iii iv Acknowledgments To my supervisor, Prof. Sérgio Reis Cunha, for allowing me to enter into the VORSat world with which I strongly identified myself. To Prof. for his guidance, endless support, contagious enthusiasm and for always trusting in me and my capabilities. I also want to thank all VORSat team for helping me integrating into the project, the long conversations we had on this work possibilities and for their patience while explaining me every detail of VORSat project. To the European Space Agency for sponsoring my participation in the first Conference in the IAA University CubeSat Satellites and Missions of the Winter Workshop Session in Rome. Conference in which I learned a lot, that allowed me to learn about various projects increasing my motivation to develop this thesis. They were classmates, but in these last six months have become more than colleagues. For the games and the support, thank you, Alexandre Gomes, Mariana Magalhaes and Paulo Pereira. To all my dear Friends for their support and assistance over the years. Throughout the univer- sity time I acquired knowledge, soft skills but nothing compares to the friendships that I acquired during my stay at FEUP. A very special thanks to my closest ones, Sónia, Hugo, Tiago, Filipe, Pedro and Miguel. Although I have already been grateful to my closest friends, I want to show my special thanks to one of the people who was always there when I needed throughout this years. To you, Teresa, for your patience with me during all this years and while reviewing and advising me about this thesis. This thesis would not be a thesis if it had not been for your love and support, I can not thank you enough! Lastly, however more important, I wish to thank my parents, my sister and Luís, for instill the values and principles that have been guiding my life and have made me the person I am today. It all starts and ends at family and it is impossible to thank properly for everything they represent and do for me. Thank you one and all. v vi "It is difficult to say what is impossible, for the dream of yesterday is the hope of today and reality of tomorrow." Robert Goddard vii viii Contents 1 Introduction 1 1.1 Motivation . 1 1.2 Objectives and Work Organization . 3 1.3 Structure . 3 2 Case Study Presentation 5 2.1 CubeSat . 5 2.1.1 QB50 . 6 2.2 Project . 7 2.2.1 Project’ Vision and Objectives . 7 2.2.2 GAMA-Sat . 7 2.2.3 VORSat . 10 2.3 Summary . 12 3 Literature Review 13 3.1 Satellites . 13 3.1.1 Satellites Features . 14 3.1.2 Satellites Classification by Altitude . 15 3.2 Navigation System . 18 3.2.1 Principles of Orbital Motion . 18 3.2.2 Orbital Motion as a Two-Body Problem . 19 3.2.3 Orbit Determination Methods . 26 3.3 Perturbed Orbits . 29 3.3.1 Atmospheric models . 31 3.4 Interaction Station - Satellite . 33 3.4.1 Measuring from the Earth . 33 3.4.2 Measuring from Space . 34 3.4.3 Communication . 37 3.5 Summary . 38 4 Orbit and Location of De-orbiting Parameters Determination 39 4.1 Problem Description . 39 4.1.1 Case study Parameters . 40 4.1.2 Kalman Filter Algorithm . 42 4.1.3 Least-Squares Estimation Algorithm . 44 4.1.4 Methods Assessment . 46 4.2 Prediction of the Decay . 47 4.3 Summary . 49 ix x CONTENTS 5 Implementation and Results 51 5.1 Orbit Prediction . 51 5.1.1 Position and Velocity . 52 5.1.2 Kalman Filter . 54 5.2 Test Cases . 60 5.2.1 Unkown Inputs Parameters Values . 60 5.2.2 Accuracy of Kalman filter . 62 5.2.3 Observations only with positions . 64 5.3 De-orbiting Location Prediction . 64 5.4 Summary . 65 6 Conclusion and Future Work 67 6.1 Main Results . 67 6.2 Work’s Assessment . 67 6.3 Future Work . 68 A Time and Coordinate Systems 69 A.1 Time . 69 A.1.1 Sidereal Time . 69 A.1.2 Universal Time . 69 A.2 Coordinates . 71 A.2.1 Geographic Coordinates . 71 A.2.2 Cartesian Coordinates . 71 A.2.3 Datum . 73 B Futher Analysis of the Results 75 B.1 TLE file used in the simulations . 75 B.2 Kalman Filter Performance . 75 B.3 Unkown Inputs Parameters Values . 76 C Futher Analysis of the Results - Continue 91 C.1 Accuracy of Kalman Filter . 91 C.2 Observations only with positions . 91 References 97 List of Figures 1.1 Work Plan . 3 2.1 First draft of VORSat/GAMA-Sat architecture [1] . 8 2.2 GAMA-Sat Structure [1] . 9 2.3 Capsule phases. Courtesy of João Gomes . 10 2.4 Capsule Structure. Courtesy of João Gomes . 11 2.5 Interior of the Capsule. Adapted from [2] . 11 2.6 Batery Charge [1] . 11 3.1 Evolution of satellites over the years . 14 3.2 The two-boy motion [3] . 20 3.3 Motion of an orbiting body [4] . 23 3.4 Keplerian Elements . 24 3.5 Procedure of the Kalman Filter . 28 3.6 Ground Station. [5] . 34 3.7 Equipment ON/OFF state depending on battery charge. [5] . 35 5.1 Loop to perform the propagation .
Load more

Recommended publications
  • Analysis of Perturbations and Station-Keeping Requirements in Highly-Inclined Geosynchronous Orbits
    ANALYSIS OF PERTURBATIONS AND STATION-KEEPING REQUIREMENTS IN HIGHLY-INCLINED GEOSYNCHRONOUS ORBITS Elena Fantino(1), Roberto Flores(2), Alessio Di Salvo(3), and Marilena Di Carlo(4) (1)Space Studies Institute of Catalonia (IEEC), Polytechnic University of Catalonia (UPC), E.T.S.E.I.A.T., Colom 11, 08222 Terrassa (Spain), [email protected] (2)International Center for Numerical Methods in Engineering (CIMNE), Polytechnic University of Catalonia (UPC), Building C1, Campus Norte, UPC, Gran Capitan,´ s/n, 08034 Barcelona (Spain) (3)NEXT Ingegneria dei Sistemi S.p.A., Space Innovation System Unit, Via A. Noale 345/b, 00155 Roma (Italy), [email protected] (4)Department of Mechanical and Aerospace Engineering, University of Strathclyde, 75 Montrose Street, Glasgow G1 1XJ (United Kingdom), [email protected] Abstract: There is a demand for communications services at high latitudes that is not well served by conventional geostationary satellites. Alternatives using low-altitude orbits require too large constellations. Other options are the Molniya and Tundra families (critically-inclined, eccentric orbits with the apogee at high latitudes). In this work we have considered derivatives of the Tundra type with different inclinations and eccentricities. By means of a high-precision model of the terrestrial gravity field and the most relevant environmental perturbations, we have studied the evolution of these orbits during a period of two years. The effects of the different perturbations on the constellation ground track (which is more important for coverage than the orbital elements themselves) have been identified. We show that, in order to maintain the ground track unchanged, the most important parameters are the orbital period and the argument of the perigee.
    [Show full text]
  • Astrodynamics
    Politecnico di Torino SEEDS SpacE Exploration and Development Systems Astrodynamics II Edition 2006 - 07 - Ver. 2.0.1 Author: Guido Colasurdo Dipartimento di Energetica Teacher: Giulio Avanzini Dipartimento di Ingegneria Aeronautica e Spaziale e-mail: [email protected] Contents 1 Two–Body Orbital Mechanics 1 1.1 BirthofAstrodynamics: Kepler’sLaws. ......... 1 1.2 Newton’sLawsofMotion ............................ ... 2 1.3 Newton’s Law of Universal Gravitation . ......... 3 1.4 The n–BodyProblem ................................. 4 1.5 Equation of Motion in the Two-Body Problem . ....... 5 1.6 PotentialEnergy ................................. ... 6 1.7 ConstantsoftheMotion . .. .. .. .. .. .. .. .. .... 7 1.8 TrajectoryEquation .............................. .... 8 1.9 ConicSections ................................... 8 1.10 Relating Energy and Semi-major Axis . ........ 9 2 Two-Dimensional Analysis of Motion 11 2.1 ReferenceFrames................................. 11 2.2 Velocity and acceleration components . ......... 12 2.3 First-Order Scalar Equations of Motion . ......... 12 2.4 PerifocalReferenceFrame . ...... 13 2.5 FlightPathAngle ................................. 14 2.6 EllipticalOrbits................................ ..... 15 2.6.1 Geometry of an Elliptical Orbit . ..... 15 2.6.2 Period of an Elliptical Orbit . ..... 16 2.7 Time–of–Flight on the Elliptical Orbit . .......... 16 2.8 Extensiontohyperbolaandparabola. ........ 18 2.9 Circular and Escape Velocity, Hyperbolic Excess Speed . .............. 18 2.10 CosmicVelocities
    [Show full text]
  • Stability of the Moons Orbits in Solar System in the Restricted Three-Body
    Stability of the Moons orbits in Solar system in the restricted three-body problem Sergey V. Ershkov, Institute for Time Nature Explorations, M.V. Lomonosov's Moscow State University, Leninskie gory, 1-12, Moscow 119991, Russia e-mail: [email protected] Abstract: We consider the equations of motion of three-body problem in a Lagrange form (which means a consideration of relative motions of 3-bodies in regard to each other). Analyzing such a system of equations, we consider in details the case of moon‟s motion of negligible mass m₃ around the 2-nd of two giant-bodies m₁, m₂ (which are rotating around their common centre of masses on Kepler’s trajectories), the mass of which is assumed to be less than the mass of central body. Under assumptions of R3BP, we obtain the equations of motion which describe the relative mutual motion of the centre of mass of 2-nd giant-body m₂ (Planet) and the centre of mass of 3-rd body (Moon) with additional effective mass m₂ placed in that centre of mass (m₂ + m₃), where is the dimensionless dynamical parameter. They should be rotating around their common centre of masses on Kepler‟s elliptic orbits. For negligible effective mass (m₂ + m₃) it gives the equations of motion which should describe a quasi-elliptic orbit of 3-rd body (Moon) around the 2-nd body m₂ (Planet) for most of the moons of the Planets in Solar system. But the orbit of Earth‟s Moon should be considered as non-constant elliptic motion for the effective mass 0.0178m₂ placed in the centre of mass for the 3-rd body (Moon).
    [Show full text]
  • Orbit Options for an Orion-Class Spacecraft Mission to a Near-Earth Object
    Orbit Options for an Orion-Class Spacecraft Mission to a Near-Earth Object by Nathan C. Shupe B.A., Swarthmore College, 2005 A thesis submitted to the Faculty of the Graduate School of the University of Colorado in partial fulfillment of the requirements for the degree of Master of Science Department of Aerospace Engineering Sciences 2010 This thesis entitled: Orbit Options for an Orion-Class Spacecraft Mission to a Near-Earth Object written by Nathan C. Shupe has been approved for the Department of Aerospace Engineering Sciences Daniel Scheeres Prof. George Born Assoc. Prof. Hanspeter Schaub Date The final copy of this thesis has been examined by the signatories, and we find that both the content and the form meet acceptable presentation standards of scholarly work in the above mentioned discipline. iii Shupe, Nathan C. (M.S., Aerospace Engineering Sciences) Orbit Options for an Orion-Class Spacecraft Mission to a Near-Earth Object Thesis directed by Prof. Daniel Scheeres Based on the recommendations of the Augustine Commission, President Obama has pro- posed a vision for U.S. human spaceflight in the post-Shuttle era which includes a manned mission to a Near-Earth Object (NEO). A 2006-2007 study commissioned by the Constellation Program Advanced Projects Office investigated the feasibility of sending a crewed Orion spacecraft to a NEO using different combinations of elements from the latest launch system architecture at that time. The study found a number of suitable mission targets in the database of known NEOs, and pre- dicted that the number of candidate NEOs will continue to increase as more advanced observatories come online and execute more detailed surveys of the NEO population.
    [Show full text]
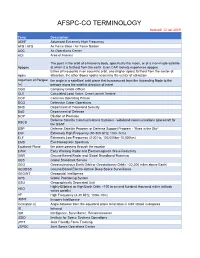
  • AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
    AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance
    [Show full text]
  • The Velocity Dispersion Profile of the Remote Dwarf Spheroidal Galaxy
    The Velocity Dispersion Profile of the Remote Dwarf Spheroidal Galaxy Leo I: A Tidal Hit and Run? Mario Mateo1, Edward W. Olszewski2, and Matthew G. Walker3 ABSTRACT We present new kinematic results for a sample of 387 stars located in and around the Milky Way satellite dwarf spheroidal galaxy Leo I. These spectra were obtained with the Hectochelle multi-object echelle spectrograph on the MMT, and cover the MgI/Mgb lines at about 5200A.˚ Based on 297 repeat measure- ments of 108 stars, we estimate the mean velocity error (1σ) of our sample to be 2.4 km/s, with a systematic error of 1 km/s. Combined with earlier re- ≤ sults, we identify a final sample of 328 Leo I red giant members, from which we measure a mean heliocentric radial velocity of 282.9 0.5 km/s, and a mean ± radial velocity dispersion of 9.2 0.4 km/s for Leo I. The dispersion profile of ± Leo I is essentially flat from the center of the galaxy to beyond its classical ‘tidal’ radius, a result that is unaffected by contamination from field stars or binaries within our kinematic sample. We have fit the profile to a variety of equilibrium dynamical models and can strongly rule out models where mass follows light. Two-component Sersic+NFW models with tangentially anisotropic velocity dis- tributions fit the dispersion profile well, with isotropic models ruled out at a 95% confidence level. Within the projected radius sampled by our data ( 1040 pc), ∼ the mass and V-band mass-to-light ratio of Leo I estimated from equilibrium 7 models are in the ranges 5-7 10 M⊙ and 9-14 (solar units), respectively.
    [Show full text]
  • Stellar Dynamics and Stellar Phenomena Near a Massive Black Hole
    Stellar Dynamics and Stellar Phenomena Near A Massive Black Hole Tal Alexander Department of Particle Physics and Astrophysics, Weizmann Institute of Science, 234 Herzl St, Rehovot, Israel 76100; email: [email protected] | Author's original version. To appear in Annual Review of Astronomy and Astrophysics. See final published version in ARA&A website: www.annualreviews.org/doi/10.1146/annurev-astro-091916-055306 Annu. Rev. Astron. Astrophys. 2017. Keywords 55:1{41 massive black holes, stellar kinematics, stellar dynamics, Galactic This article's doi: Center 10.1146/((please add article doi)) Copyright c 2017 by Annual Reviews. Abstract All rights reserved Most galactic nuclei harbor a massive black hole (MBH), whose birth and evolution are closely linked to those of its host galaxy. The unique conditions near the MBH: high velocity and density in the steep po- tential of a massive singular relativistic object, lead to unusual modes of stellar birth, evolution, dynamics and death. A complex network of dynamical mechanisms, operating on multiple timescales, deflect stars arXiv:1701.04762v1 [astro-ph.GA] 17 Jan 2017 to orbits that intercept the MBH. Such close encounters lead to ener- getic interactions with observable signatures and consequences for the evolution of the MBH and its stellar environment. Galactic nuclei are astrophysical laboratories that test and challenge our understanding of MBH formation, strong gravity, stellar dynamics, and stellar physics. I review from a theoretical perspective the wide range of stellar phe- nomena that occur near MBHs, focusing on the role of stellar dynamics near an isolated MBH in a relaxed stellar cusp.
    [Show full text]
  • A Highly Elliptical Orbit Space System for Hydrometeorological Monitoring of the Arctic Region by V
    A highly elliptical orbit space system for hydrometeorological monitoring of the Arctic region by V. V. Asmus1, V. N. Dyadyuchenko2, Y. I. Nosenko3, G. M. Polishchuk4 and V. A. Selin3 The lack of reliable, frequently high latitudes. It has therefore been • Monitoring of climate change updated information on the Earth’s suggested that demonstration of polar ice caps is a signifi cant problem a hydrometeorological system of • Data collection and relay for weather forecasting, affecting satellites on highly elliptical orbit from land-, sea- and air-based forecast skill for the entire planet. The (HEO), called the “Arctica” system, observing platforms poor numerical weather prediction should be created to provide the (NWP) skill for the Arctic region necessary complex information for the • Exchange and dissemination of and the Earth’s northern territories diffi cult tasks involved in developing processed hydrometeorological is caused primarily by errors in the whole Arctic region. and heliogeophysical data. determining initial conditions, which depend on the quality of initial Signifi cantly, the hydrometeorological Further progress in global and data. Until now, initial data have observations carried out in the regional numerical weather prediction been received from meteorological Arctic within the framework of the depends to a large extent on: geostationary satellites, which are International Polar Year 2007-2008 not very effective in scanning high are not provided with remote-sensing • Quasi-continuous reception latitudes and polar-orbiting
    [Show full text]
  • GPS Applications in Space
    Space Situational Awareness 2015: GPS Applications in Space James J. Miller, Deputy Director Policy & Strategic Communications Division May 13, 2015 GPS Extends the Reach of NASA Networks to Enable New Space Ops, Science, and Exploration Apps GPS Relative Navigation is used for Rendezvous to ISS GPS PNT Services Enable: • Attitude Determination: Use of GPS enables some missions to meet their attitude determination requirements, such as ISS • Real-time On-Board Navigation: Enables new methods of spaceflight ops such as rendezvous & docking, station- keeping, precision formation flying, and GEO satellite servicing • Earth Sciences: GPS used as a remote sensing tool supports atmospheric and ionospheric sciences, geodesy, and geodynamics -- from monitoring sea levels and ice melt to measuring the gravity field ESA ATV 1st mission JAXA’s HTV 1st mission Commercial Cargo Resupply to ISS in 2008 to ISS in 2009 (Space-X & Cygnus), 2012+ 2 Growing GPS Uses in Space: Space Operations & Science • NASA strategic navigation requirements for science and 20-Year Worldwide Space Mission space ops continue to grow, especially as higher Projections by Orbit Type* precisions are needed for more complex operations in all space domains 1% 5% Low Earth Orbit • Nearly 60%* of projected worldwide space missions 27% Medium Earth Orbit over the next 20 years will operate in LEO 59% GeoSynchronous Orbit – That is, inside the Terrestrial Service Volume (TSV) 8% Highly Elliptical Orbit Cislunar / Interplanetary • An additional 35%* of these space missions that will operate at higher altitudes will remain at or below GEO – That is, inside the GPS/GNSS Space Service Volume (SSV) Highly Elliptical Orbits**: • In summary, approximately 95% of projected Example: NASA MMS 4- worldwide space missions over the next 20 years will satellite constellation.
    [Show full text]
  • Open Rosen Thesis.Pdf
    THE PENNSYLVANIA STATE UNIVERSITY SCHREYER HONORS COLLEGE DEPARTMENT OF AEROSPACE ENGINEERING END OF LIFE DISPOSAL OF SATELLITES IN HIGHLY ELLIPTICAL ORBITS MITCHELL ROSEN SPRING 2019 A thesis submitted in partial fulfillment of the requirements for a baccalaureate degree in Aerospace Engineering with honors in Aerospace Engineering Reviewed and approved* by the following: Dr. David Spencer Professor of Aerospace Engineering Thesis Supervisor Dr. Mark Maughmer Professor of Aerospace Engineering Honors Adviser * Signatures are on file in the Schreyer Honors College. i ABSTRACT Highly elliptical orbits allow for coverage of large parts of the Earth through a single satellite, simplifying communications in the globe’s northern reaches. These orbits are able to avoid drastic changes to the argument of periapse by using a critical inclination (63.4°) that cancels out the first level of the geopotential forces. However, this allows the next level of geopotential forces to take over, quickly de-orbiting satellites. Thus, a balance between the rate of change of the argument of periapse and the lifetime of the orbit is necessitated. This thesis sets out to find that balance. It is determined that an orbit with an inclination of 62.5° strikes that balance best. While this orbit is optimal off of the critical inclination, it is still near enough that to allow for potential use of inclination changes as a deorbiting method. Satellites are deorbited when the propellant remaining is enough to perform such a maneuver, and nothing more; therefore, the less change in velocity necessary for to deorbit, the better. Following the determination of an ideal highly elliptical orbit, the different methods of inclination change is tested against the usual method for deorbiting a satellite, an apoapse burn to lower the periapse, to find the most propellant- efficient method.
    [Show full text]
  • PNT in High Earth Orbit and Beyond
    International Committee on GNSS-13 Focuses on PNT in High Earth Orbit and Beyond Since last reported in the November/December 2016 issue of Inside GNSS, signicant progress has been made to extend the use of Global Navigation Satellite Systems (GNSS) for Positioning, Navigation, and Timing (PNT) in High Earth Orbit (HEO). This update describes the results of international eorts that are enabling mission planners to condently Artist’s rendering employ GNSS signals in HEO and how researchers are of Orion docked to the lunar-orbiting extending the use of GNSS out to lunar distances. Gateway. Image courtesy of NASA tarting with nascent GPS space to existing ones, multi-GNSS signal Moving from Dream to Reality flight experiments in Low- availability in HEO is set to improve Within the National Aeronautics and SEarth Orbit (LEO) in the 1980s significantly. Users could soon Space Administration (NASA), the and 1990s, space-borne GPS is now employ four operational global con- Space Communications and Naviga- commonplace. Researchers continue stellations and two regional space- tion (SCaN) Program Office leads expanding GPS and GNSS use into— based navigation and augmenta- eorts in PNT development and policy. and beyond—the Space Service Vol- tion systems, respectively: the U.S. Numerous missions have been own in ume (SSV), which is the volume of GPS, Russia’s GLONASS, Europe’s the SSV, dating back to the rst ight space surrounding the Earth between Galileo, China’s BeiDou (BDS), experiments in 1997. NASA, through 3,000 kilometers and Geosynchronous Japan’s Quasi-Zenith Satellite Sys- SCaN and its predecessors, has sup- (GEO) altitudes.
    [Show full text]
  • PHY140Y 3 Properties of Gravitational Orbits
    PHY140Y 3 Properties of Gravitational Orbits 3.1 Overview • Orbits and Total Energy • Elliptical, Parabolic and Hyperbolic Orbits 3.2 Characterizing Orbits With Energy Two point particles attracting each other via gravity will cause them to move, as dictated by Newton’s laws of motion. If they start from rest, this motion will simply be along the line separating the two points. It is a one-dimensional problem, and easily solved. The two objects collide. If the two objects are given some relative motion to start with, then it is easy to convince yourself that a collision is no longer possible (so long as these particles are point-like). In our discussion of orbits, we will only consider the special case where one object of mass M is much heavier than the smaller object of mass m. In this case, although the larger object is accelerated toward the smaller one, we will ignore that acceleration and assume that the heavier object is fixed in space. There are three general categories of motion, when there is some relative motion, which we can characterize by the total energy of the object, i.e., E ≡ K + U (1) 1 GMm = mv2 − , (2) 2 r2 where K and U are the kinetic and gravitational energy, respectively. 3.3 Energy < 0 In this case, since the total energy is negative, it is not possible for the object to get too far from the mass M, since E = K + U<0 (3) 1 GMm ⇒ mv2 = + E (4) 2 r GM ⇒ r = (5) 1 2 − E 2 v m GM ⇒ r< , (6) −E since r will take on its maximum value when the denominator is minimized (or when v is the smallest value possible, ie.
    [Show full text]