AVG and RMS Values of Periodic Waveforms
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Glossary Physics (I-Introduction)
1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay. -

Effect of Moisture Distribution on Velocity and Waveform of Ultrasonic-Wave Propagation in Mortar
materials Article Effect of Moisture Distribution on Velocity and Waveform of Ultrasonic-Wave Propagation in Mortar Shinichiro Okazaki 1,* , Hiroma Iwase 2, Hiroyuki Nakagawa 3, Hidenori Yoshida 1 and Ryosuke Hinei 4 1 Faculty of Engineering and Design, Kagawa University, 2217-20 Hayashi, Takamatsu, Kagawa 761-0396, Japan; [email protected] 2 Chuo Consultants, 2-11-23 Nakono, Nishi-ku, Nagoya, Aichi 451-0042, Japan; [email protected] 3 Shikoku Research Institute Inc., 2109-8 Yashima, Takamatsu, Kagawa 761-0113, Japan; [email protected] 4 Building Engineering Group, Civil Engineering and Construction Department, Shikoku Electric Power Co., Inc., 2-5 Marunouchi, Takamatsu, Kagawa 760-8573, Japan; [email protected] * Correspondence: [email protected] Abstract: Considering that the ultrasonic method is applied for the quality evaluation of concrete, this study experimentally and numerically investigates the effect of inhomogeneity caused by changes in the moisture content of concrete on ultrasonic wave propagation. The experimental results demonstrate that the propagation velocity and amplitude of the ultrasonic wave vary for different moisture content distributions in the specimens. In the analytical study, the characteristics obtained experimentally are reproduced by modeling a system in which the moisture content varies between the surface layer and interior of concrete. Keywords: concrete; ultrasonic; water content; elastic modulus Citation: Okazaki, S.; Iwase, H.; 1. Introduction Nakagawa, H.; Yoshida, H.; Hinei, R. Effect of Moisture Distribution on As many infrastructures deteriorate at an early stage, long-term structure management Velocity and Waveform of is required. If structural deterioration can be detected as early as possible, the scale of Ultrasonic-Wave Propagation in repair can be reduced, decreasing maintenance costs [1]. -
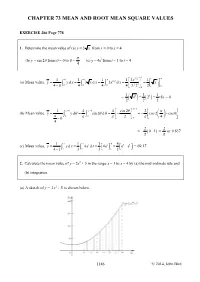
Chapter 73 Mean and Root Mean Square Values
CHAPTER 73 MEAN AND ROOT MEAN SQUARE VALUES EXERCISE 286 Page 778 1. Determine the mean value of (a) y = 3 x from x = 0 to x = 4 π (b) y = sin 2θ from θ = 0 to θ = (c) y = 4et from t = 1 to t = 4 4 3/2 4 44 4 4 1 1 11/2 13x 13 (a) Mean value, y= ∫∫ yxd3d3d= xx= ∫ x x= = x − 00 0 0 4 0 4 4 4 3/20 2 1 11 = 433=( 2) = (8) = 4 2( ) 22 π /4 1 ππ/4 4 /4 4 cos 2θπ 2 (b) Mean value, yy=dθ = sin 2 θθ d =−=−−cos 2 cos 0 π ∫∫00ππ24 π − 0 0 4 2 2 = – (01− ) = or 0.637 π π 144 1 144 (c) Mean value, y= yxd= 4ett d t = 4e = e41 − e = 69.17 41− ∫∫11 3 31 3 2. Calculate the mean value of y = 2x2 + 5 in the range x = 1 to x = 4 by (a) the mid-ordinate rule and (b) integration. (a) A sketch of y = 25x2 + is shown below. 1146 © 2014, John Bird Using 6 intervals each of width 0.5 gives mid-ordinates at x = 1.25, 1.75, 2.25, 2.75, 3.25 and 3.75, as shown in the diagram x 1.25 1.75 2.25 2.75 3.25 3.75 y = 25x2 + 8.125 11.125 15.125 20.125 26.125 33.125 Area under curve between x = 1 and x = 4 using the mid-ordinate rule with 6 intervals ≈ (width of interval)(sum of mid-ordinates) ≈ (0.5)( 8.125 + 11.125 + 15.125 + 20.125 + 26.125 + 33.125) ≈ (0.5)(113.75) = 56.875 area under curve 56.875 56.875 and mean value = = = = 18.96 length of base 4− 1 3 3 4 44 1 1 2 1 2x 1 128 2 (b) By integration, y= yxd = 2 x + 5 d x = +5 x = +20 −+ 5 − ∫∫11 41 3 3 31 3 3 3 1 = (57) = 19 3 This is the precise answer and could be obtained by an approximate method as long as sufficient intervals were taken 3. -

Introduction to Noise Radar and Its Waveforms
sensors Article Introduction to Noise Radar and Its Waveforms Francesco De Palo 1, Gaspare Galati 2 , Gabriele Pavan 2,* , Christoph Wasserzier 3 and Kubilay Savci 4 1 Department of Electronic Engineering, Tor Vergata University of Rome, now with Rheinmetall Italy, 00131 Rome, Italy; [email protected] 2 Department of Electronic Engineering, Tor Vergata University and CNIT-Consortium for Telecommunications, Research Unit of Tor Vergata University of Rome, 00133 Rome, Italy; [email protected] 3 Fraunhofer Institute for High Frequency Physics and Radar Techniques FHR, 53343 Wachtberg, Germany; [email protected] 4 Turkish Naval Research Center Command and Koc University, Istanbul, 34450 Istanbul,˙ Turkey; [email protected] * Correspondence: [email protected] Received: 31 July 2020; Accepted: 7 September 2020; Published: 11 September 2020 Abstract: In the system-level design for both conventional radars and noise radars, a fundamental element is the use of waveforms suited to the particular application. In the military arena, low probability of intercept (LPI) and of exploitation (LPE) by the enemy are required, while in the civil context, the spectrum occupancy is a more and more important requirement, because of the growing request by non-radar applications; hence, a plurality of nearby radars may be obliged to transmit in the same band. All these requirements are satisfied by noise radar technology. After an overview of the main noise radar features and design problems, this paper summarizes recent developments in “tailoring” pseudo-random sequences plus a novel tailoring method aiming for an increase of detection performance whilst enabling to produce a (virtually) unlimited number of noise-like waveforms usable in different applications. -

Oscillating Currents
Oscillating Currents • Ch.30: Induced E Fields: Faraday’s Law • Ch.30: RL Circuits • Ch.31: Oscillations and AC Circuits Review: Inductance • If the current through a coil of wire changes, there is an induced emf proportional to the rate of change of the current. •Define the proportionality constant to be the inductance L : di εεε === −−−L dt • SI unit of inductance is the henry (H). LC Circuit Oscillations Suppose we try to discharge a capacitor, using an inductor instead of a resistor: At time t=0 the capacitor has maximum charge and the current is zero. Later, current is increasing and capacitor’s charge is decreasing Oscillations (cont’d) What happens when q=0? Does I=0 also? No, because inductor does not allow sudden changes. In fact, q = 0 means i = maximum! So now, charge starts to build up on C again, but in the opposite direction! Textbook Figure 31-1 Energy is moving back and forth between C,L 1 2 1 2 UL === UB === 2 Li UC === UE === 2 q / C Textbook Figure 31-1 Mechanical Analogy • Looks like SHM (Ch. 15) Mass on spring. • Variable q is like x, distortion of spring. • Then i=dq/dt , like v=dx/dt , velocity of mass. By analogy with SHM, we can guess that q === Q cos(ωωω t) dq i === === −−−ωωωQ sin(ωωω t) dt Look at Guessed Solution dq q === Q cos(ωωω t) i === === −−−ωωωQ sin(ωωω t) dt q i Mathematical description of oscillations Note essential terminology: amplitude, phase, frequency, period, angular frequency. You MUST know what these words mean! If necessary review Chapters 10, 15. -

The Physics of Sound 1
The Physics of Sound 1 The Physics of Sound Sound lies at the very center of speech communication. A sound wave is both the end product of the speech production mechanism and the primary source of raw material used by the listener to recover the speaker's message. Because of the central role played by sound in speech communication, it is important to have a good understanding of how sound is produced, modified, and measured. The purpose of this chapter will be to review some basic principles underlying the physics of sound, with a particular focus on two ideas that play an especially important role in both speech and hearing: the concept of the spectrum and acoustic filtering. The speech production mechanism is a kind of assembly line that operates by generating some relatively simple sounds consisting of various combinations of buzzes, hisses, and pops, and then filtering those sounds by making a number of fine adjustments to the tongue, lips, jaw, soft palate, and other articulators. We will also see that a crucial step at the receiving end occurs when the ear breaks this complex sound into its individual frequency components in much the same way that a prism breaks white light into components of different optical frequencies. Before getting into these ideas it is first necessary to cover the basic principles of vibration and sound propagation. Sound and Vibration A sound wave is an air pressure disturbance that results from vibration. The vibration can come from a tuning fork, a guitar string, the column of air in an organ pipe, the head (or rim) of a snare drum, steam escaping from a radiator, the reed on a clarinet, the diaphragm of a loudspeaker, the vocal cords, or virtually anything that vibrates in a frequency range that is audible to a listener (roughly 20 to 20,000 cycles per second for humans). -

Airspace: Seeing Sound Grades
National Aeronautics and Space Administration GRADES K-8 Seeing Sound airspace Aeronautics Research Mission Directorate Museum in a BO SerieXs www.nasa.gov MUSEUM IN A BOX Materials: Seeing Sound In the Box Lesson Overview PVC pipe coupling Large balloon In this lesson, students will use a beam of laser light Duct tape to display a waveform against a flat surface. In doing Super Glue so, they will effectively“see” sound and gain a better understanding of how different frequencies create Mirror squares different sounds. Laser pointer Tripod Tuning fork Objectives Tuning fork activator Students will: 1. Observe the vibrations necessary to create sound. Provided by User Scissors GRADES K-8 Time Requirements: 30 minutes airspace 2 Background The Science of Sound Sound is something most of us take for granted and rarely do we consider the physics involved. It can come from many sources – a voice, machinery, musical instruments, computers – but all are transmitted the same way; through vibration. In the most basic sense, when a sound is created it causes the molecule nearest the source to vibrate. As this molecule is touching another molecule it causes that molecule to vibrate too. This continues, from molecule to molecule, passing the energy on as it goes. This is also why at a rock concert, or even being near a car with a large subwoofer, you can feel the bass notes vibrating inside you. The molecules of your body are vibrating, allowing you to physically feel the music. MUSEUM IN A BOX As with any energy transfer, each time a molecule vibrates or causes another molecule to vibrate, a little energy is lost along the way, which is why sound gets quieter with distance (Fig 1.) and why louder sounds, which cause the molecules to vibrate more, travel farther. -

33600A Series Trueform Waveform Generators Generate Trueform Arbitrary Waveforms with Less Jitter, More Fidelity and Greater Resolution
DATA SHEET 33600A Series Trueform Waveform Generators Generate Trueform arbitrary waveforms with less jitter, more fidelity and greater resolution Revolutionary advances over previous generation DDS 33600A Series waveform generators with exclusive Trueform signal generation technology offer more capability, fidelity and flexibility than previous generation Direct Digital Synthesis (DDS) generators. Use them to accelerate your development Trueform process from start to finish. – 1 GSa/s sampling rate and up to 120 MHz bandwidth Better Signal Integrity – Arbs with sequencing and up to 64 MSa memory – 1 ps jitter, 200x better than DDS generators – 5x lower harmonic distortion than DDS – Compatible with Keysight Technologies, DDS Inc. BenchVue software Over the past two decades, DDS has been the waveform generation technology of choice in function generators and economical arbitrary waveform generators. Reduced Jitter DDS enables waveform generators with great frequency resolution, convenient custom waveforms, and a low price. <1 ps <200 ps As with any technology, DDS has its limitations. Engineers with exacting requirements have had to either work around the compromised performance or spend up to 5 times more for a high-end, point-per-clock waveform generator. Keysight Technologies, Inc. Trueform Trueform technology DDS technology technology offers an alternative that blends the best of DDS and point-per-clock architectures, giving you the benefits of both without the limitations of either. Trueform technology uses an exclusive digital 0.03% -

The Oscilloscope and the Function Generator: Some Introductory Exercises for Students in the Advanced Labs
The Oscilloscope and the Function Generator: Some introductory exercises for students in the advanced labs Introduction So many of the experiments in the advanced labs make use of oscilloscopes and function generators that it is useful to learn their general operation. Function generators are signal sources which provide a specifiable voltage applied over a specifiable time, such as a \sine wave" or \triangle wave" signal. These signals are used to control other apparatus to, for example, vary a magnetic field (superconductivity and NMR experiments) send a radioactive source back and forth (M¨ossbauer effect experiment), or act as a timing signal, i.e., \clock" (phase-sensitive detection experiment). Oscilloscopes are a type of signal analyzer|they show the experimenter a picture of the signal, usually in the form of a voltage versus time graph. The user can then study this picture to learn the amplitude, frequency, and overall shape of the signal which may depend on the physics being explored in the experiment. Both function generators and oscilloscopes are highly sophisticated and technologically mature devices. The oldest forms of them date back to the beginnings of electronic engineering, and their modern descendants are often digitally based, multifunction devices costing thousands of dollars. This collection of exercises is intended to get you started on some of the basics of operating 'scopes and generators, but it takes a good deal of experience to learn how to operate them well and take full advantage of their capabilities. Function generator basics Function generators, whether the old analog type or the newer digital type, have a few common features: A way to select a waveform type: sine, square, and triangle are most common, but some will • give ramps, pulses, \noise", or allow you to program a particular arbitrary shape. -

True RMS, Trueinrush®, and True Megohmmeter®
“WATTS CURRENT” TECHNICAL BULLETIN Issue 09 Summer 2016 True RMS, TrueInRush®, and True Megohmmeter ® f you’re a user of AEMC® instruments, you may have come across the terms True IRMS, TrueInRush®, and/or True Megohmmeter ®. In this article, we’ll briefly define what these terms mean and why they are important to you. True RMS The most well-known of these is True RMS, an industry term for a method for calculating Root Mean Square. Root Mean Square, or RMS, is a mathematical concept used to derive the average of a constantly varying value. In electronics, RMS provides a way to measure effective AC power that allows you to compare it to the equivalent heating value of a DC system. Some low-end instruments employ a technique known as “average sensing,” sometimes referred to as “average RMS.” This entails multiplying the peak AC voltage or current by 0.707, which represents the decimal form of one over the square root of two. For electrical systems where the AC cycle is sinusoidal and reasonably undistorted, this can produce accurate and reliable results. Unfortunately, for other AC waveforms, such as square waves, this calculation can introduce significant inaccuracies. The equation can also be problematic when the AC wave is non-linear, as would be found in systems where the original or fundamental wave is distorted by one or more harmonic waves. In these cases, we need to apply a method known as “true” RMS. This involves a more generalized mathematical calculation that takes into consideration all irregularities and asymmetries that may be present in the AC waveform: In this equation, n equals the number of measurements made during one complete cycle of the waveform. -
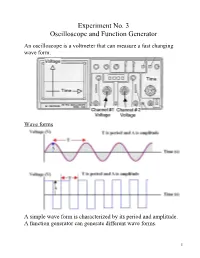
Experiment No. 3 Oscilloscope and Function Generator
Experiment No. 3 Oscilloscope and Function Generator An oscilloscope is a voltmeter that can measure a fast changing wave form. Wave forms A simple wave form is characterized by its period and amplitude. A function generator can generate different wave forms. 1 Part 1 of the experiment (together) Generate a square wave of frequency of 1.8 kHz with the function generator. Measure the amplitude and frequency with the Fluke DMM. Measure the amplitude and frequency with the oscilloscope. 2 The voltage amplitude has 2.4 divisions. Each division means 5.00 V. The amplitude is (5)(2.4) = 12.0 V. The Fluke reading was 11.2 V. The period (T) of the wave has 2.3 divisions. Each division means 250 s. The period is (2.3)(250 s) = 575 s. 1 1 f 1739 Hz The frequency of the wave = T 575 10 6 The Fluke reading was 1783 Hz The error is at least 0.05 divisions. The accuracy can be improved by displaying the wave form bigger. 3 Now, we have two amplitudes = 4.4 divisions. One amplitude = 2.2 divisions. Each division = 5.00 V. One amplitude = 11.0 V Fluke reading was 11.2 V T = 5.7 divisions. Each division = 100 s. T = 570 s. Frequency = 1754 Hz Fluke reading was 1783 Hz. It was always better to get a bigger display. 4 Part 2 of the experiment -Measuring signals from the DVD player. Next turn on the DVD Player and turn on the accessory device that is attached to the top of the DVD player. -

Peak and Root-Mean-Square Accelerations Radiated from Circular Cracks and Stress-Drop Associated with Seismic High-Frequency Radiation
J. Phys. Earth, 31, 225-249, 1983 PEAK AND ROOT-MEAN-SQUARE ACCELERATIONS RADIATED FROM CIRCULAR CRACKS AND STRESS-DROP ASSOCIATED WITH SEISMIC HIGH-FREQUENCY RADIATION Teruo YAMASHITA Earthquake Research Institute, the University of Tokyo, Tokyo, Japan (Received July 25, 1983) We derive an approximate expression for far-field spectral amplitude of acceleration radiated by circular cracks. The crack tip velocity is assumed to make abrupt changes, which can be the sources of high-frequency radiation, during the propagation of crack tip. This crack model will be usable as a source model for the study of high-frequency radiation. The expression for the spectral amplitude of acceleration is obtained in the following way. In the high-frequency range its expression is derived, with the aid of geometrical theory of diffraction, by extending the two-dimensional results. In the low-frequency range it is derived on the assumption that the source can be regarded as a point. Some plausible assumptions are made for its behavior in the intermediate- frequency range. Theoretical expressions for the root-mean-square and peak accelerations are derived by use of the spectral amplitude of acceleration obtained in the above way. Theoretically calculated accelerations are compared with observed ones. The observations are shown to be well explained by our source model if suitable stress-drop and crack tip velocity are assumed. Using Brune's model as an earthquake source model, Hanks and McGuire showed that the seismic ac- celerations are well predicted by a stress-drop which is higher than the statically determined stress-drop. However, their conclusion seems less reliable since Brune's source model cannot be applied to the study of high-frequency radiation.