THE ANISOTROPIC TRUNCATED KERNEL METHOD for CONVOLUTION with FREE-SPACE GREEN's FUNCTIONS\Ast
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

AUGUST 1984 LH: I Wanted to Sit In, If Conway Would Let Me
VOL. 8, NO. 8 Cover Photo by Robert Herman FEATURES LEVON HELM During the late '60s and early '70s, Bob Dylan and The Band were musically a winning combination, due in part to the drumming and singing talents of Levon Helm. The Band went on to record many classics until their breakup in 1976. Here, Levon discusses his background, his work with Dylan and The Band, and the various projects he has been involved with during the past few years. by Robyn Flans 8 THOMMY PRICE Price, one of the hottest new drummers on the scene today, is cur- rently the power behind Billy Idol. Before joining Idol, Thommy Carneau had a five-year gig with Mink DeVille, followed by a year with Fred Scandal. In this interview, Thommy reveals the responsibilities of by working with a top act, his experiences with music video, and how Photo the rock 'n' roll life-style is not all glamour. by Connie Fisher 14 BOB MOSES Bob Moses is truly an original personality in the music world. Although he is known primarily in the jazz idiom for his masterful drumming, he is also an active composer and artist. He talks about his influences, his technique, and the philosophies behind his Jachles various forms of self-expression. by Chip Stern 18 Michael by DRUMMING IN ATLANTIC CITY Photo by Rick Van Horn 22 Malkin WILL DOWER Rick Australian Sessionman by by Rick Van Horn 24 Photo CLUB SCENE ON THE MOVE COLUMNS Attention To Detail James D. Miller and Bob Pignatiello. 78 by Rick Van Horn 90 IN THE STUDIO EDUCATION DRUM SOLOIST Jim Plank CONCEPTS Philly Joe Jones: "Lazy Bird" by Ted Dyer 84 Drummers And Put-Downs by Dan Tomlinson 96 by Roy Burns 28 REVIEWS EQUIPMENT LISTENER'S GUIDE ON TRACK 46 by Peter Erskine and Denny Carmassi 30 PRODUCT CLOSE-UP NEWS ROCK PERSPECTIVES Remo PTS Update Beat Study #13 by Bob Saydlowski, Jr. -

Spartan Dail Student Services, Pages 4,5
Inside The Entertainer Spartan Dail Student Services, pages 4,5 Volume 78 No 39 Serving the San Jose Community Since 1934 Thursday. April 1, 1982 New counseling center combines programs By Scott Wird students," according to a program brochure. recruitment efforts. Its self-stated purpose is to "bring - MESA, a tutoring and counseling The Educational Opportunity Program, It provides counseling, tutoring, and The Learning Resource Center will together in a single location . all the program. which provides help for disadvantaged financial aid assistance for students provide a central place for the various servies present resources devoted to assisting - Student Affirmative Action Referral minority and low-income students, will no "disadvantaged" sociologically or that are "fragmented" throughout the students with learning problems." Center. longer provide counseling services. economically. university, according to Martin. Renaming the General Education Ad- -Writing Lab. Starting next fall, that function will be The program also helps students enter Martin said he hopes the center will be visement Center the "Academic Advisement -Reading Lab. handled by various other programs in a the university who cannot meet regular en- located in the old I Wahlquist I library Center" would broaden its functions to in- -Mathematics Clinic. central Learning Assistance Center. trance requirements. building. Fullerton wants the center, and clude advisement on general education, -Logic Lab. The basic restructuring of EOP ahd many In a memo describing the changes, other proposals in the memo established by undeclared major, special major, and second -Electronic Learning Lab. other tutoring and counseling programs was Hobert Burns, academic vice president and next fall, he said. -
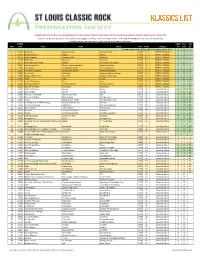
KLASSICS LIST Criteria
KLASSICS LIST criteria: 8 or more points (two per fan list, two for U-Man A-Z list, two to five for Top 95, depending on quartile); 1984 or prior release date Sources: ten fan lists (online and otherwise; see last page for details) + 2011-12 U-Man A-Z list + 2014 Top 95 KSHE Klassics (as voted on by listeners) sorted by points, Fan Lists count, Top 95 ranking, artist name, track name SLCRPS UMan Fan Top ID # ID # Track Artist Album Year Points Category A-Z Lists 95 35 songs appeared on all lists, these have green count info >> X 10 n 1 12404 Blue Mist Mama's Pride Mama's Pride 1975 27 PERFECT KLASSIC X 10 1 2 12299 Dead And Gone Gypsy Gypsy 1970 27 PERFECT KLASSIC X 10 2 3 11672 Two Hangmen Mason Proffit Wanted 1969 27 PERFECT KLASSIC X 10 5 4 11578 Movin' On Missouri Missouri 1977 27 PERFECT KLASSIC X 10 6 5 11717 Remember the Future Nektar Remember the Future 1973 27 PERFECT KLASSIC X 10 7 6 10024 Lake Shore Drive Aliotta Haynes Jeremiah Lake Shore Drive 1971 27 PERFECT KLASSIC X 10 9 7 11654 Last Illusion J.F. Murphy & Salt The Last Illusion 1973 27 PERFECT KLASSIC X 10 12 8 13195 The Martian Boogie Brownsville Station Brownsville Station 1977 27 PERFECT KLASSIC X 10 13 9 13202 Fly At Night Chilliwack Dreams, Dreams, Dreams 1977 27 PERFECT KLASSIC X 10 14 10 11696 Mama Let Him Play Doucette Mama Let Him Play 1978 27 PERFECT KLASSIC X 10 15 11 11547 Tower Angel Angel 1975 27 PERFECT KLASSIC X 10 19 12 11730 From A Dry Camel Dust Dust 1971 27 PERFECT KLASSIC X 10 20 13 12131 Rosewood Bitters Michael Stanley Michael Stanley 1972 27 PERFECT