Photometric Stereo with Applications in Material Classification
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Page 1 of 5 MSDS for #23884 - ALEENES TACKY GLUE Page 2 of 5
MSDS for #23884 - ALEENES TACKY GLUE Page 1 of 5 Item Numbers: 23884-1004, 23884-1008 Page 1 of 5 MSDS for #23884 - ALEENES TACKY GLUE Page 2 of 5 Item Numbers: 23884-1004, 23884-1008 Page 2 of 5 MSDS for #23884 - ALEENES TACKY GLUE Page 3 of 5 Item Numbers: 23884-1004, 23884-1008 Page 3 of 5 MSDS for #23884 - ALEENES TACKY GLUE Page 4 of 5 Item Numbers: 23884-1004, 23884-1008 Page 4 of 5 MSDS for #23884 - ALEENES TACKY GLUE Page 5 of 5 Item Numbers: 23884-1004, 23884-1008 Page 5 of 5 MATERIAL SAFETY DATA SHEET Issue Date: 01/16/2008 ========================================================================================================== SECTION I - PRODUCT IDENTIFICATION ------------------------------------------------------------------------------------------------------------------------------------------------ Product Name: Anita’s Acrylic Yard & Garden Craft Paint Product Nos: 11801- 11832 Product Sizes: 2 fl. oz, 8 fl. oz. Product Class: Water Based Paint ========================================================================================================== SECTION II - HAZARDOUS INGREDIENTS ------------------------------------------------------------------------------------------------------------------------------------------------ None ========================================================================================================== SECTION III - PHYSICAL & CHEMICAL DATA ------------------------------------------------------------------------------------------------------------------------------------------------ -

Certified Products List
THE ART & CREATIVE MATERIALS INSTITUTE, INC. Street Address: 1280 Main St., 2nd Floor Mailing Address: P.O. Box 479 Hanson, MA 02341 USA Tel. (781) 293-4100 Fax (781) 294-0808 www.acminet.org Certified Products List March 28, 2007 & ANSI Performance Standard Z356._X BUY PRODUCTS THAT BEAR THE ACMI SEALS Products Authorized to Bear the Seals of The Certification Program of THE ART & CREATIVE MATERIALS INSTITUTE, INC. Since 1940, The Art & Creative Materials Institute, Inc. (“ACMI”) has been evaluating and certifying art, craft, and other creative materials to ensure that they are properly labeled. This certification program is reviewed by ACMI’s Toxicological Advisory Board. Over the years, three certification seals had been developed: The CP (Certified Product) Seal, the AP (Approved Product) Seal, and the HL (Health Label) Seal. In 1998, ACMI made the decision to simplify its Seals and scale the number of Seals used down to two. Descriptions of these new Seals and the Seals they replace follow: New AP Seal: (replaces CP Non-Toxic, CP, AP Non-Toxic, AP, and HL (No Health Labeling Required). Products bearing the new AP (Approved Product) Seal of the Art & Creative Materials Institute, Inc. (ACMI) are certified in a program of toxicological evaluation by a medical expert to contain no materials in sufficient quantities to be toxic or injurious to humans or to cause acute or chronic health problems. These products are certified by ACMI to be labeled in accordance with the chronic hazard labeling standard, ASTM D 4236 and the U.S. Labeling of Hazardous NO HEALTH LABELING REQUIRED Art Materials Act (LHAMA) and there is no physical hazard as defined with 29 CFR Part 1910.1200 (c). -

Paperworld China: Highly Anticipated 2019 Nichole Chang Tel
Press release 13 November 2019 Paperworld China: highly anticipated 2019 Nichole Chang Tel. +852 2230 9226 edition opens from 15 November nichole.chang@ hongkong.messefrankfurt.com www.messefrankfurt.com.hk www.paperworldchina.com PWC19_OR Paperworld China – the leading trade fair for the stationery, office supplies and hobby and crafts sectors in Asia – kicks off from 15 November at the National Exhibition and Convention Center (Shanghai). In its 15th edition, the show will occupy 23,000 sqm of exhibition space in Hall 5.1 and welcome 424 exhibitors from 15 countries and regions. Exhibitors from Austria, China, France, Germany, Hong Kong, India, Israel, Japan, Lithuania, Malaysia, South Korea, Spain, Switzerland, Taiwan and the United States will showcase the most cutting-edge stationery products at the fair. Owing to its well established reputation, the fair has attracted renowned brands such as Beifa, Brita, Comix, Daycraft, Guangbo, Kodomo No Kao, Kumamon, Mcusta, Mindwave, Monami, Morning Glory, Pelikan, Pilot, Platinum, Sakura, Shanghai Marie, Tsukineko, Umajirushi, Wacom, and Zebra. As in previous years, four distinct zones: Stationery and Hobby, Tomorrow’s Office, Cultural and Creative, and Quality Suppliers will inspire the likes of major retailers and distributors with new product ideas and stationery trends. Fostering original brands, building an integrated platform Alongside the rise of Chinese stationery brands in recent years, Paperworld China has continued to support business and cultural exchange. The fair has promoted creative brands and excellent original designs, helping to connect them with new sales channels and distribution partners. Just one avenue through which this has been achieved is the ‘Best Stationery of China BSOC’ awards, which help companies to boost their brand exposure. -

Plim Trading Inc Updated Pricelist As of 7-20-2020
Category Quantity UOM Item Code Item Description Wholesale Price Acetate BOX SFAX-A4 SUPERFAX ACETATE TRANSPARENCY FILM A4 (210MM X 297MM X 0.1MM) 230.00 Activity SET BINGO BINGO SET 80.00 Activity PC BL-ABA BOOKLET - ABAKADA 7.00 Activity PC BL-ALA BOOKLET - ALAMAT 7.00 Activity PC BL-BUG BOOKLET - BUGTONG 7.00 Activity PC BL-CP BOOKLET - COLORING PAD (ORDINARY) 7.00 Activity PC BL-PAB BOOKLET - PABULA 7.00 Activity PC BL-SB BOOKLET - STORY BOOK (ORDINARY) 7.00 Activity PC COL-STORY COLORED STORY BOOK 13.00 Activity SET 3462 DOMS MATHEMATICAL DRAWING INTRUMENT BOX 39.00 Activity PC PCLOCK PAPER CLOCK 6.00 Activity PC PTE1218 PERIODIC TABLE OF ELEMENTS 1218 (BIG) 9.00 Activity PC PTE912 PERIODIC TABLE OF ELEMENTS 9X12 (SMALL) 5.50 Activity SET P-MONEY PLAY MONEY 33.00 Activity PC POCKETBOOK POCKET BOOK - TAGALOG/ENGLISH 13.00 Activity PACK POP-C POPSICLE STICK - COLORED (50PCS/PACK) 10.00 Activity PACK POP-P POPSICLE STICK - PLAIN (50PCS/PACK) 9.00 Activity PC SB-ELFE SMART BOOK - EL FELIBUSTERISMO 33.00 Activity PC SB-FLOR SMART BOOK - FLORANTE AT LAURA 33.00 Activity PC SB-IA SMART BOOK - IBONG ADARNA 33.00 Activity PC SB-NOLI SMART BOOK - NOLI ME TANGERE 33.00 Activity PACK WC-A1 WINDOW CARD (50PCS/PACK) A1 100.00 Activity PACK WC-A2 WINDOW CARD (50PCS/PACK) A2 100.00 Activity PACK WC-A3 WINDOW CARD (50PCS/PACK) A3 100.00 Activity PACK WC-A4 WINDOW CARD (50PCS/PACK) A4 100.00 Activity PACK WC-D1 WINDOW CARD (50PCS/PACK) D1 100.00 Activity PACK WC-D2 WINDOW CARD (50PCS/PACK) D2 100.00 Activity PACK WC-D3 WINDOW CARD (50PCS/PACK) D3 -

Brush Pen Size Guides
Downstroke Size Guide You might have a huge collection of pens, but did you know that you can't treat them all the same? Your lettering size has to change with the specific pen. A brush script "e" is the best letter to test a pen out with. The pen should allow you to write at a size that allows the loop of the "e" to be the same width (or a hair more) than the width of the widest downstroke. It should also be large enough to form a beautiful teardrop shape inside of the loop. Use the pen grouping worksheets to know which size guide worksheet would work best for each of your pen. Practicing with each pen at the proper size will allow you to make your lettering skills shine! xo, Extra Sma Brush Pens: Cocoiro Letter Pen Monami Plus Pen 3000 Enzō by Pilot Sma Brush Pens: Zebra Funwari Fude Brush Pen Tombow Fudenosuke Hard Nib Pilot Futayaku Double-Sided Brush Pen Zebra Disposable Brush Pen (Extra Fine) Sma Medium Brush Pens: Tombow Fudenosuke Soft Nib Pentel Brush Tip Sign Pen Zebra Disposable Brush Pen (Fine) Crayola Super Tips Pigma FB Kuretake Fudegokochi All Rights Reserved. For Personal, non-commercial Use only. © 2020 Amanda Arneill Ltd | amandaarneill.com Not for resale, reuse, or distribution of any kind . Medium Brush Pens: Sharpie Brush Tip Pen (Zipper Case) Caran D’Ache Fibralo Brush Sakura Pigma Brush Stabilo Pen 68 Brush Marker Faber Castell PITT Artist Pen (B) All Rights Reserved. For Personal, non-commercial Use only. © 2020 Amanda Arneill Ltd | amandaarneill.com Not for resale, reuse, or distribution of any kind . -

Product Catalogue St Ationery & Office Supplies
www.prokope.co.za PRODUCT CATALOGUE ST ATIONERY & OFFICE SUPPLIES 2021 CONTENTS ABOUT US 01 PAPER AND BOARDS 02-04 GLUE AND ADHESIVE TAPES 05-07 WRITING AND DRAWING 08-13 BOOKS AND WRITING PADS 14-16 PRINTING SUPPLIES 17-18 ENVELOPES AND FILING 19-21 DESK ACCESSORIES AND ESSENTIALS 22-26 1 ABOUT US Prokope Enterprises provides competitive prices for a wide variety of high- quality goods and services. As a one-stop shop, we are here to help you accomplish the goals and priorities you are passionate about, by providing you with commodities that you need in your day to day running. As a supplier of stationery and office supplies, we pride in giving you the best quality products and office solutions. B-BBEE LEVEL 1 Here are some of the famous, quality brands we supply: 2 PAPER & BOARDS 01 PAPER AND BOARDS 3 Typek - Copy Paper Mondi Rotatrim - Copy Paper Typek - Copy Paper Mondi – Maestro Colored Paper PE001 A4 White 500 Sheets PE003 A4 White 500 Sheets PE005 A4 White 500 Sheets PE006 A4 White 500 Sheets PE002 A3 White 500 Sheets PE004 A3 White 500 Sheets PE007 A3 White 500 Sheets Typek – White Board Typek – Tinted Pastel Board Colorjet – Laser Copier Paper Colorjet - Photo Paper PE008 A4 White 500 Sheets PE009 A4 Paste 100 Sheets PE010 A4 130gsm 250 Pack PE013 A4 Matte 200, 100, 50 Pack PE011 A4 150gsm 250 Pack PE014 A4 Satin Pearl 20 Pack PE012 A4 250gsm 250 Pack PE015 A4 Iron on Transfer 5, 10 Pack 01 PAPER AND BOARDS 4 Waltons – Self-Adhesive Notes PE022 38mm x 50mm 100 sheets Printer Rolls Computer Paper – Continuous Feed Fax Paper Roll PE023 70mm x 75mm 100 sheets PE016 Bond till Rolls 50, 100 / Box PE018 Black Console PE021 13mm Core 20 Rolls / Box PE024 75mm x 75mm 100 sheets PE017 Thermal till Rolls 50 / Box PE019 Without Down Perforations PE025 75mm x 100mm 100 sheets PE020 With Down Perforations PE025 75mm x 125mm 100 sheets Waltons – Self-Adhesive Neon Notes 3M Post-it – Self-Adhesive Notes Waltons – Highlighters & Page Markers 3M Post-it – Sign Here Pads PE026 38mm x 50mm 300-sheet cube PE029 Post-it. -
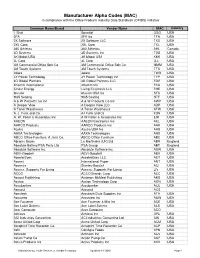
MAC List for Website.Xlsx
Manufacturer Alpha Codes (MAC) in compliance with the Office Products Industry Data Standards (OPIDS) Initiative Common Name/Brand Vendor Name MAC Country 1 Shot Spraylat OSG USA 2FA 2FA Inc TFA USA 2X Software 2X Software LLC TXS USA 2XL Corp. 2XL Corp TXL USA 360 Athletics 360 Athletics AHL Canada 3D Systems 3D Systems Inc TDS USA 3K Mobel USA 3K Mobel USA KKK USA 3L Corp 3L Corp LLL USA 3M Commercial Office Sply Co 3M Commercial Office Sply Co MMM USA 3M Touch Systems 3M Touch Systems TTS USA 3ware 3ware TWR USA 3Y Power Technology 3Y Power Technology Inc TYP USA 4D Global Partners 4D Global Partners LLC FDG USA 4Kamm International 4Kamm Intl FKA USA 5-hour Energy Living Essentials LLC FHE USA 6fusion 6fusion USA Inc SFU USA 9to5 Seating 9to5 Seating NTF USA A & W Products Co Inc A & W Products Co Inc AWP USA A Deeper View A Deeper View LLC ADP USA A Toner Warehouse A Toner Warehouse ATW USA A. J. Funk and Co. AJ Funk and Co FUN USA A. W. Peller & Associates Inc A W Peller & Associates Inc EIM USA AAEON AAEON Electronics Inc AEL USA AARCO Products AARCO Products Inc AAR USA Aastra Aastra USA Inc AAS USA AAXA Technologies AAXA Technologies AAX USA ABCO Office Furniture, A Jami Co. ABCO Office Furniture ABC USA Abrams Books La Martinière (UK) Ltd ABR England Absolute Battery/PSA Parts Ltd. PSA Group ABT England Absolute Software Inc. Absolute Software Inc ASW USA ABVI-Goodwill ABVI-Goodwill ABV USA AccelerEyes AccelerEyes LLC AEY USA Accent International Paper ANT USA Accentra Stanley-Bostitch ACI USA Access: Supports For Living Access: -
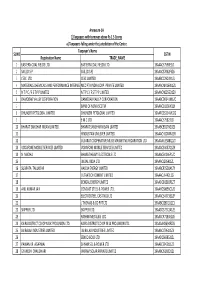
FINAL DISTRIBUTION.Xlsx
Annexure-1A 1)Taxpayers with turnover above Rs 1.5 Crores a) Taxpayers falling under the jurisdiction of the Centre Taxpayer's Name SL NO GSTIN Registration Name TRADE_NAME 1 EASTERN COAL FIELDS LTD. EASTERN COAL FIELDS LTD. 19AAACE7590E1ZI 2 SAIL (D.S.P) SAIL (D.S.P) 19AAACS7062F6Z6 3 CESC LTD. CESC LIMITED 19AABCC2903N1ZL 4 MATERIALS CHEMICALS AND PERFORMANCE INTERMEDIARIESMCC PTA PRIVATE INDIA CORP.LIMITED PRIVATE LIMITED 19AAACM9169K1ZU 5 N T P C / F S T P P LIMITED N T P C / F S T P P LIMITED 19AAACN0255D1ZV 6 DAMODAR VALLEY CORPORATION DAMODAR VALLEY CORPORATION 19AABCD0541M1ZO 7 BANK OF NOVA SCOTIA 19AAACB1536H1ZX 8 DHUNSERI PETGLOBAL LIMITED DHUNSERI PETGLOBAL LIMITED 19AAFCD5214M1ZG 9 E M C LTD 19AAACE7582J1Z7 10 BHARAT SANCHAR NIGAM LIMITED BHARAT SANCHAR NIGAM LIMITED 19AABCB5576G3ZG 11 HINDUSTAN UNILEVER LIMITED 19AAACH1004N1ZR 12 GUJARAT COOPERATIVE MILKS MARKETING FEDARATION LTD 19AAAAG5588Q1ZT 13 VODAFONE MOBILE SERVICES LIMITED VODAFONE MOBILE SERVICES LIMITED 19AAACS4457Q1ZN 14 N MADHU BHARAT HEAVY ELECTRICALS LTD 19AAACB4146P1ZC 15 JINDAL INDIA LTD 19AAACJ2054J1ZL 16 SUBRATA TALUKDAR HALDIA ENERGY LIMITED 19AABCR2530A1ZY 17 ULTRATECH CEMENT LIMITED 19AAACL6442L1Z7 18 BENGAL ENERGY LIMITED 19AADCB1581F1ZT 19 ANIL KUMAR JAIN CONCAST STEEL & POWER LTD.. 19AAHCS8656C1Z0 20 ELECTROSTEEL CASTINGS LTD 19AAACE4975B1ZP 21 J THOMAS & CO PVT LTD 19AABCJ2851Q1Z1 22 SKIPPER LTD. SKIPPER LTD. 19AADCS7272A1ZE 23 RASHMI METALIKS LTD 19AACCR7183E1Z6 24 KAIRA DISTRICT CO-OP MILK PRO.UNION LTD. KAIRA DISTRICT CO-OP MILK PRO.UNION LTD. 19AAAAK8694F2Z6 25 JAI BALAJI INDUSTRIES LIMITED JAI BALAJI INDUSTRIES LIMITED 19AAACJ7961J1Z3 26 SENCO GOLD LTD. 19AADCS6985J1ZL 27 PAWAN KR. AGARWAL SHYAM SEL & POWER LTD. 19AAECS9421J1ZZ 28 GYANESH CHAUDHARY VIKRAM SOLAR PRIVATE LIMITED 19AABCI5168D1ZL 29 KARUNA MANAGEMENT SERVICES LIMITED 19AABCK1666L1Z7 30 SHIVANANDAN TOSHNIWAL AMBUJA CEMENTS LIMITED 19AAACG0569P1Z4 31 SHALIMAR HATCHERIES LIMITED SHALIMAR HATCHERIES LTD 19AADCS6537J1ZX 32 FIDDLE IRON & STEEL PVT. -

Editorial Board
ESTEEM Academic Journal Vol.16, December 2020 VOLUME 16, DECEMBER 2020 Universiti Teknologi MARA, Cawangan Pulau Pinang EDITORIAL BOARD ADVISORS Prof. Ts Dr Salmiah Kasolang, Universiti Teknologi MARA Pulau Pinang, Malaysia Associate Prof. Dr. Nor Aziyah Bakhari, Universiti Teknologi MARA Pulau Pinang, CHIEF EDITOR Dr Nor Salwa Damanhuri, Universiti Teknologi MARA Pulau Pinang, Malaysia INTERNATIONAL ADVISORY BOARD Distinguish Prof J. Geoffrey Chase, University of Canterbury, New Zealand Dr. Prateek Benhal, University of Maryland, USA Dr. Ra'ed M. Al-Khatib, Yarmouk University, Jordan MANAGING EDITOR Dr. Ainorkhilah Mahmood, Universiti Teknologi MARA Pulau Pinang, Malaysia TECHNICAL EDITOR Dr. Syarifah Adilah Mohamed Yusoff, Universiti Teknologi MARA Pulau Pinang, Malaysia EDITORS Associate Prof Dr. Azrina Md Ralib, International Islamic University Malaysia Dr. Salina Alias, Universiti Teknologi MARA Pulau Pinang, Malaysia Dr. Vicinisvarri Inderan, Universiti Teknologi MARA Pulau Pinang, Malaysia LANGUAGE EDITORS Suzana Binti Ab. Rahim, Universiti Teknologi MARA Pulau Pinang, Malaysia Isma Noornisa Ismail, Universiti Teknologi MARA Pulau Pinang, Malaysia Dr. Mah Boon Yih, Universiti Teknologi MARA Pulau Pinang, Malaysia p-ISSN 1675-7939; e-ISSN 2289-4934 ©2020 Universiti Teknologi MARA Cawangan Pulau Pinang ESTEEM Academic Journal Vol.16, December 2020 FOREWORD th Welcome to the 16 Volume of ESTEEM Academic Journal for December 2020 issue: an online peer-referred academic journal by Universiti Teknologi MARA, Cawangan Pulau Pinang, which focusing on innovation in science and technology that covers areas and disciplines of Engineering, Computer and Information Sciences, Health and Medical Sciences, Cognitive and Behavioral Sciences, Applied Sciences and Application in Mathematics and Statistics. It is a pleasure to announce that ESTEEM Academic Journal has been successfully indexed in Asean Citation Index and MyCite, a significant move, which will increase the chance for this journal to be indexed in SCOPUS. -

P-Lim Trading Pricelist 070821
Wholesale Category QTY UOM Item Code Item Description Brand Price Acetate - Film BOX SFAX-A4 SUPERFAX ACETATE TRANSPARENCY FILM A4 (210MM X 297MM X 0.1MM) 250.00 Superfax Activity SET BINGO BINGO SET 80.00 Generic Activity PC BL-ABA BOOKLET - ABAKADA 7.00 Generic Activity PC BL-ALA BOOKLET - ALAMAT 7.00 Generic Activity PC BL-BUG BOOKLET - BUGTONG 7.00 Generic Activity PC BL-CP BOOKLET - COLORING PAD (ORDINARY) 7.00 Generic Activity PC BL-PAB BOOKLET - PABULA 7.00 Generic Activity PC BL-SB BOOKLET - STORY BOOK (ORDINARY) 7.00 Generic Activity PC BL-TULA BOOKLET - TULANG PAMBATA 7.00 Generic Activity PC COL-STORY COLORED STORY BOOK 13.00 Generic Activity PC PCLOCK PAPER CLOCK 6.00 Generic Activity PC PTE1218 PERIODIC TABLE OF ELEMENTS 1218 (BIG) 9.00 Generic Activity PC PTE912 PERIODIC TABLE OF ELEMENTS 9X12 (SMALL) 5.50 Generic Activity SET P-MONEY PLAY MONEY 33.00 Generic Activity PACK POP-C POPSICLE STICK - COLORED (50PCS/PACK) 10.00 Generic Activity PACK POP-P POPSICLE STICK - PLAIN (50PCS/PACK) 9.00 Generic Activity PACK WC-A1 WINDOW CARD (50PCS/PACK) A1 100.00 Generic Activity PACK WC-A2 WINDOW CARD (50PCS/PACK) A2 100.00 Generic Activity PACK WC-A3 WINDOW CARD (50PCS/PACK) A3 100.00 Generic Activity PACK WC-A4 WINDOW CARD (50PCS/PACK) A4 100.00 Generic Activity PACK WC-D1 WINDOW CARD (50PCS/PACK) D1 100.00 Generic Activity PACK WC-D2 WINDOW CARD (50PCS/PACK) D2 100.00 Generic Activity PACK WC-D3 WINDOW CARD (50PCS/PACK) D3 100.00 Generic Activity PACK WC-D4 WINDOW CARD (50PCS/PACK) D4 100.00 Generic Activity PACK WC-M1 WINDOW CARD -

BID TABULATION BID #2806 (Req. 156526)
BID #2806 (Req. 156526) BID TABULATION PYRAMID LN Qty Unit Description/Product ID OFFICE BRAND SCHOOL BRAND SOLUTIONS PRODUCTS 2 360 1420990 TAPE, BOOK, TRANSPARENT, 2"WX540"L, ,***1420990 NO BID $3.70 04 99 OR EQUAL ** 3M 04 3M 845 MINIMUM 12/CS 3 180 1420995 TAPE, BOOK, TRANSPARENT, 3"WX540"L, ,***1420995 NO BID $5.66 04 99 OR EQUAL ** 3M 04 3M 845 12/CS 4 96 1510015 WASTEBASKET, RECTANGULAR PLASTIC 12 3/4"DIA X 16 1/4"H, 7 GALLON, GRAY OR BLACK ,***1510015 NO BID $4.49 07 99 OR EQUAL 01 RUBBERMAID #2830 02 LOMA 823 ** 3M 03 RUBBERMAID 2956 15X11X15 RECTANGULAR MIN 96 12/CS 04 TENEX 16024 RECT. 7 GAL 05 RUBBERMAID 69179 06 RUBBERMAID 69176 (BLACK) 221-481 07 CONTINENTAL 2818BK 5 576 1510020 BINDER, 3 RING, 1" CAPACITY, BLUE VINYL ,***1510020 $1.22 10 $0.97 10 99 OR EQUAL 01 VERNON #25-2832 12 PER CASE 02 MEAD 25-2832 ** 03 K311-1 K&M CO. SAMSILL 04 ASSOCIATED L2-A1181-BE MINIMUM $800 IN 05 ASSOCIATED C1181-BE FULL 06 BOORUM PEASE 88730-1 CASES 07 WILSON JONES 368-14 NBC 08 AVERY DENNISON K311-10 09 WILSON JONES 27616 10 SAMSILL 11302 PYRAMID LN Qty Unit Description/Product ID OFFICE BRAND SCHOOL BRAND SOLUTIONS PRODUCTS 6 180 15100251420990 BINDER,TAPE, BOOK, 3 RING, TRANSPARENT, 2" CAPACITY, 2"WX540"L, BLUE VINYL ,***1420990 ,***1510025 NO BID $1.69 08 99 OR EQUAL NOT 01 VERNON #25-4832 ACCEPTA BLE** 02 MEAD #25-4832 SAMSILL 03 K311-2 K&M CO. -

Hong Kong, September 2017 Paperworld China China
Press Hong Kong, September 2017 Paperworld China Stavie Hung China International Stationery and Office Supplies Exhibition Tel. +852 2238 9907 [email protected]. Shanghai New International Expo Centre com Shanghai, China, 21 – 23 September 2017 www.messefrankfurt.com.hk www.paperworldchina.com PWC17_OR Leading industry players from around the world prepare for the opening of Paperworld China 2017 “Small yet Beautiful” and “Oriental Sense Zone” form impressive show schedule Concurrent fringe events offer insight from all corners of the industry The 13 th edition of Paperworld China, the highly anticipated trade fair dedicated to the stationery and office supplies industry in China, will take place from 21 – 23 September 2017 at the Shanghai New International Expo Centre in China. With strong industry support from around the world, the 2017 edition will host a total of 548 exhibitors from 13 countries and regions, including China, France, Germany, India, Italy, Japan, Korea, New Zealand, Serbia, Switzerland, the UK, Hong Kong and Taiwan. With the show’s opening day just around the corner, numerous global renowned brands are preparing to present their latest products, market insight and industry knowledge to worldwide visitors. Some of the biggest participating names include Akashiya, Amos, Aneos, Beifa, Comix, Dahle, Durable, Edu3, Elco, etranger di costarica, Fas, Guangbo, Hamanaka, Herma, Kidstoyo, Languo, Lion, Lyra, Mindwave, Monami, Morning Glory, Online, Papier Imperial, Pilot, Platinum, Premce, Schneider, Sdi, Snowwhite, Sunwood, Topstick, Treein Art, Tsukineko, Zebra and many more. In addition, product pavilions from Chinese regions including Yiwu, Wenzhou, Qingyuan, Ningbo, Fujian, Taiwan and Hong Kong, will also be a key highlight of the 2017 fair, with each area’s participants looking to demonstrate their innovative products, as well as share the latest Messe Frankfurt (HK) Ltd industry developments from their respective regions.