Limits to Tertiary Astrometric Companions in Binary Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2017 Býk Otec Fir 2016 Býk Otec Fir 2015 Býk
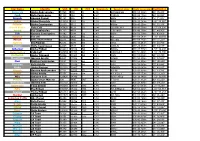
2017 BÝK OTEC FIR 2016 BÝK OTEC FIR 2015 BÝK OTEC FIR 2014 BÝK OTEC FIR 1 2949 LEGACY FRAZZLED 507 2 2944 NASHVILLE DYNASTY 551 BÝCI REGISTROVANÍ V ČR 3 2933 RIVETING FRAZZLED 614 Aktualizace k: 5.1.2019 1 2920 CHARL CHARLEY 551 BÝCI *2017 a starší. TPI 2400 a více 4 2919 PINNACLE 7 MTS 5 2913 AltaLAWSON AltaROBSON 11 Natural, Zooservis 6 2908 DISCJOCKEY FORTUNE 200 Ostatní 7 2908 FULLMARKS FORTUNE 200 8 2908 EISAKU SAMURI 507 9 2907 ACURA ACHIEVER 29 10 2904 BUNDLE ACHIEVER 29 11 2903 DEDICATE SUPERHERO 551 12 2902 PURSUIT IMAX 200 13 2893 EMERALD FORTUNE 200 14 2893 AltaRNR AltaROBSON 11 15 2889 ROME FRAZZLED 614 16 2883 RENEGADE JALTAOAK 550 17 2883 SOLUTION FRAZZLED 614 18 2883 BATMAN IMAX 200 19 2882 ROYAL DUKE 29 20 2882 PONCHO NOBLE 551 21 2879 CHALLENGER SUPERHERO 200 22 2878 PERK SPECTRE 29 23 2878 CRIMSON SPECTRE 29 24 2876 MAESTRO IMAX 200 25 2874 GAMECHANGER MODESTY 1 26 2873 PYRAMID GUARANTEE 200 27 2873 MENACE DELTA-WORTH 551 28 2872 APPLEBEES ACHIEVER 29 29 2872 CASCADE KING ROYAL 507 30 2870 AltaROBERT AltaROBSON 11 31 2869 ARISTOCRAT FRAZZLED 515 32 2869 RAPID RUBI-HAZE 551 33 2867 AltaROADY AltaROBSON 11 34 2866 BIG AL FRAZZLED 507 35 2866 PETRO PROPHECY 29 36 2866 VALUE DUKE 29 37 2865 NACASH SUPERHERO 180 38 2865 EMBELLISH FORTUNE 200 39 2864 BRASS FRAZZLED 507 40 2861 MESCALERO PINNACLE 250 41 2860 KORBEL ACHIEVER 1 42 2860 TIMBERLAKE IMAX 200 43 2860 AltaHOTJOB HOTLINE 11 44 2859 ENFORCE FRAZZLED 100 45 2858 HEMINGWAY FORTUNE 200 46 2857 EXODUS REASON 250 47 2857 ALERT FORTUNE 200 48 2856 DIVERSITY MEDLEY 29 49 2856 -

Solar Writer Report for Abraham Lincoln
FIXED STARS A Solar Writer Report for Abraham Lincoln Written by Diana K Rosenberg Compliments of:- Stephanie Johnson Seeing With Stars Astrology PO Box 159 Stepney SA 5069 Australia Tel/Fax: +61 (08) 8331 3057 Email: [email protected] Web: www.esotech.com.au Page 2 Abraham Lincoln Natal Chart 12 Feb 1809 12:40:56 PM UT +0:00 near Hodgenville 37°N35' 085°W45' Tropical Placidus 22' 13° 08°ˆ ‡ 17' ¾ 06' À ¿É ‰ 03° ¼ 09° 00° 06° 09°06° ˆ ˆ ‡ † ‡ 25° 16' 41'08' 40' † 01' 09' Œ 29' ‰ 9 10 23° ¶ 8 27°‰ 11 Ï 27° 01' ‘ ‰02' á 7 12 ‘ áá 23° á 23° ¸ 23°Š27' á Š à „ 28' 28' 6 18' 1 10°‹ º ‹37' 13° 05' ‹ 5 Á 22° ½ 27' 2 4 01' Ü 3 07° Œ ƒ » 09' 23° 09° Ý Ü 06° 16' 06' Ê 00°ƒ 13° 22' Ý 17' 08°‚ Page 23 Astrological Summary Chart Point Positions: Abraham Lincoln Planet Sign Position House Comment The Moon Capricorn 27°Cp01' 12th The Sun Aquarius 23°Aq27' 12th read into 1st House Mercury Pisces 10°Pi18' 1st Venus Aries 7°Ar27' 1st read into 2nd House Mars Libra 25°Li29' 8th Jupiter Pisces 22°Pi05' 1st Saturn Sagittarius 3°Sg08' 9th read into 10th House Uranus Scorpio 9°Sc40' 8th Neptune Sagittarius 6°Sg41' 9th read into 10th House Pluto Pisces 13°Pi37' 1st The North Node Scorpio 6°Sc09' 8th The South Node Taurus 6°Ta09' 2nd The Ascendant Aquarius 23°Aq28' 1st The Midheaven Sagittarius 8°Sg22' 10th The Part of Fortune Capricorn 27°Cp02' 12th Chart Point Aspects Planet Aspect Planet Orb App/Sep The Moon Square Mars 1°32' Separating The Moon Conjunction The Part of Fortune 0°00' Applying The Sun Trine Mars 2°02' Applying The Sun Conjunction The Ascendant -

GTO Keypad Manual, V5.001
ASTRO-PHYSICS GTO KEYPAD Version v5.xxx Please read the manual even if you are familiar with previous keypad versions Flash RAM Updates Keypad Java updates can be accomplished through the Internet. Check our web site www.astro-physics.com/software-updates/ November 11, 2020 ASTRO-PHYSICS KEYPAD MANUAL FOR MACH2GTO Version 5.xxx November 11, 2020 ABOUT THIS MANUAL 4 REQUIREMENTS 5 What Mount Control Box Do I Need? 5 Can I Upgrade My Present Keypad? 5 GTO KEYPAD 6 Layout and Buttons of the Keypad 6 Vacuum Fluorescent Display 6 N-S-E-W Directional Buttons 6 STOP Button 6 <PREV and NEXT> Buttons 7 Number Buttons 7 GOTO Button 7 ± Button 7 MENU / ESC Button 7 RECAL and NEXT> Buttons Pressed Simultaneously 7 ENT Button 7 Retractable Hanger 7 Keypad Protector 8 Keypad Care and Warranty 8 Warranty 8 Keypad Battery for 512K Memory Boards 8 Cleaning Red Keypad Display 8 Temperature Ratings 8 Environmental Recommendation 8 GETTING STARTED – DO THIS AT HOME, IF POSSIBLE 9 Set Up your Mount and Cable Connections 9 Gather Basic Information 9 Enter Your Location, Time and Date 9 Set Up Your Mount in the Field 10 Polar Alignment 10 Mach2GTO Daytime Alignment Routine 10 KEYPAD START UP SEQUENCE FOR NEW SETUPS OR SETUP IN NEW LOCATION 11 Assemble Your Mount 11 Startup Sequence 11 Location 11 Select Existing Location 11 Set Up New Location 11 Date and Time 12 Additional Information 12 KEYPAD START UP SEQUENCE FOR MOUNTS USED AT THE SAME LOCATION WITHOUT A COMPUTER 13 KEYPAD START UP SEQUENCE FOR COMPUTER CONTROLLED MOUNTS 14 1 OBJECTS MENU – HAVE SOME FUN! -

Milestone Goto-Bino Series .Cdr
Kson MilestoneK Standard Alt/Az GOTO Mount INSTRUCTIONS CONTENT FOR KSON STANDARD ALT/AZ GOTO USER INTRODUCTION.................................................................................1 ACCESSORIES..................................................................................2 ASSEMBLY INSTRUCTIONS.............................................................3 FEATURES.........................................................................5 OPERATION MANUAL FOR SKYTOUCH CONTROLLER............... 6 KEY DESCRIPTION.................................................................................6 STATUS DESCRIPTION...........................................................................6 OPERATION PROCESS...........................................................................7 POWER ON......................................................................................7 WARNING........................................................................................7 ALIGNMENT STATUS........................................................................7 CHANGE THE DATE..................................................................7 CHANGE THE TIME...................................................................8 CHANGE THE SITE...................................................................8 ALIGNMENT.............................................................................9 NAVIGATION STATUS.....................................................................11 MENU STATUS................................................................................11 -

GTO Keypad Controller, Version 4.12
ASTRO-PHYSICS GTO KEYPAD Version v4.12 Flash RAM Updates This and future keypad flash RAM updates can be accomplished through the Internet. Check our web site www.astro-physics.com periodically for further information. March 7, 2008 2 ASTRO-PHYSICS GTO KEYPAD CONTROLLER v4.12 GTO Keypad Controller 7 Layout and Buttons of the Keypad 7 Vacuum Fluorescent Display 7 N - S - E - W Directional Buttons 7 RA/DEC REV Button: 7 STOP Button 8 Number Buttons 8 <PREV and NEXT> Buttons 8 GOTO Button 8 + - Button 8 MENU Button 8 FOC Button 8 Retractable Hanger 8 Keypad Protector 9 Keypad Care and Warranty 9 New Features of Version 4.12 11 09-06-04 Version 4.12 11 08-28-04 Version 4.11 11 08-26-04 Version 4.10 11 02-16-04 Version 4.07 12 Features from version 3.2 (3.2 was only shipped with new mounts or repairs) 13 Getting Started - Do this at home, if possible 14 Setup your Mount and Cable Connections 14 Gather Basic Information 14 Enter Your Location, Date and Time 14 Practice Using your Keypad 16 Your First Observing Session with V4.12 16 Normal Startup Sequence - For Mounts That are Setup in the Field 17 Assemble Your Mount 17 Startup sequence 17 Star Sync 18 Polar Alignment – Which method to choose? 19 N Polar Calibrate - Calibrating with Polaris 19 Two-Star Calibration 20 Resume from Park 22 Resume Ref-Park 1 22 Alternate Polar Calibration Routines & Tips 23 Polar Aligning in the Daytime – Northern Hemisphere 23 Using the Astro-Physics Daytime Polar Alignment Routine in the Southern Hemisphere 25 GTO Quick Star Drift Method of Polar Alignment – Using the Meridian Delay Feature 28 Roland’s Favorite Polar Calibration Routine 31 Using Software to Improve Pointing Accuracy 31 How to Find Objects if You Have Less Than Perfect Polar Alignment or Non-Orthogonal Systems 32 What if I Lose My Calibration? 32 Auto-Connect Sequence - For Permanent, Polar-Aligned Mounts 33 3 Important Points 33 External Startup Sequence – For Mounts that are controlled by an External Computer. -
Star Name Identity SAO HD FK5 Magnitude Spectral Class Right Ascension Declination Alpheratz Alpha Andromedae 73765 358 1 2,06 B
Star Name Identity SAO HD FK5 Magnitude Spectral class Right ascension Declination Alpheratz Alpha Andromedae 73765 358 1 2,06 B8IVpMnHg 00h 08,388m 29° 05,433' Caph Beta Cassiopeiae 21133 432 2 2,27 F2III-IV 00h 09,178m 59° 08,983' Algenib Gamma Pegasi 91781 886 7 2,83 B2IV 00h 13,237m 15° 11,017' Ankaa Alpha Phoenicis 215093 2261 12 2,39 K0III 00h 26,283m - 42° 18,367' Schedar Alpha Cassiopeiae 21609 3712 21 2,23 K0IIIa 00h 40,508m 56° 32,233' Deneb Kaitos Beta Ceti 147420 4128 22 2,04 G9.5IIICH-1 00h 43,590m - 17° 59,200' Achird Eta Cassiopeiae 21732 4614 3,44 F9V+dM0 00h 49,100m 57° 48,950' Tsih Gamma Cassiopeiae 11482 5394 32 2,47 B0IVe 00h 56,708m 60° 43,000' Haratan Eta ceti 147632 6805 40 3,45 K1 01h 08,583m - 10° 10,933' Mirach Beta Andromedae 54471 6860 42 2,06 M0+IIIa 01h 09,732m 35° 37,233' Alpherg Eta Piscium 92484 9270 50 3,62 G8III 01h 13,483m 15° 20,750' Rukbah Delta Cassiopeiae 22268 8538 48 2,66 A5III-IV 01h 25,817m 60° 14,117' Achernar Alpha Eridani 232481 10144 54 0,46 B3Vpe 01h 37,715m - 57° 14,200' Baten Kaitos Zeta Ceti 148059 11353 62 3,74 K0IIIBa0.1 01h 51,460m - 10° 20,100' Mothallah Alpha Trianguli 74996 11443 64 3,41 F6IV 01h 53,082m 29° 34,733' Mesarthim Gamma Arietis 92681 11502 3,88 A1pSi 01h 53,530m 19° 17,617' Navi Epsilon Cassiopeiae 12031 11415 63 3,38 B3III 01h 54,395m 63° 40,200' Sheratan Beta Arietis 75012 11636 66 2,64 A5V 01h 54,640m 20° 48,483' Risha Alpha Piscium 110291 12447 3,79 A0pSiSr 02h 02,047m 02° 45,817' Almach Gamma Andromedae 37734 12533 73 2,26 K3-IIb 02h 03,900m 42° 19,783' Hamal Alpha -
Saul J. Adelman
SAUL J. ADELMAN Department of Physics 1434 Fairfield Avenue The Citadel Charleston, SC 29407 Charleston, SC 29409 (843) 766-5348 (843) 953-6943 CURRENT POSITION: Professor of Physics, The Citadel (Aug. 22, 1989 - to date) PAST POSITIONS: Associate Professor of Physics, The Citadel (Aug. 23, 1983 to Aug. 21, 1989) NRC-NASA Research Associate, NASA Goddard Space Flight Center (Aug. 1, 1984 - July 31, 1986) Assistant Professor of Physics, The Citadel (Aug. 21, 1978 - Aug. 22, 1983) Assistant Professor of Astronomy, Boston University (Sept. 1, 1974 - Aug. 31, 1978) NAS/NRC Postdoctoral Resident Research Associate, NASA Goddard SpaceFlight Center (Aug. 1, 1972 - Aug. 31, 1974) EDUCATION: Ph.D. in Astronomy, California Institute of Technology, June 1972; Thesis: A Study of Twenty- One Sharp-lined Non-Variable Cool Peculiar A Stars, December 1971 (Dissertation Abstracts International 33, 543-13, number 77-22, 597) B.S. in Physics with high honors and high honors in physics, University of Maryland, June 1966 ACADEMIC HONORS: Phi Beta Kappa Phi Kappa Phi Sigma Pi Sigma Sigma Xi Summer Institute in Space Physics at Columbia University 1965 NDEA Title IV Fellowship 1966-69 ARCS Foundation Fellowship 1970-71 Citadel Development Foundation Faculty Fellowship 1987-93 Faculty Achievement Award 1989, 1997 Governor’s Award for Excellence in Scientific Research at a Primarily Undergraduate Institution 2011 OBSERVING EXPERIENCE: Guest Investigator, Dominion Astrophysical Observatory 1984-2016 Guest Investigator, Hubble Space Telescope 2003-05, 2011-16 Participant -

Almanacco Astronomico 2002 – Introduzione
Almanacco Astronomico per l’anno 2002 Sergio Alessandrelli C.C.C.D.S. - Hipparcos La Luna – Principali formazioni geologiche Almanacco Astronomico per l’anno 2002 A tutti gli amici astrofili… 1 Almanacco Astronomico 2002 – Introduzione Introduzione all’Almanacco Astronomico 2002 Il presente Almanacco Astronomico è stato realizzato utilizzando comuni programmi di calcolo astronomico facilmente reperibili sul mercato del software, ovvero scaricabili gratuitamente tramite Internet. La precisione nei calcoli è quindi quella tipica per questo tipo di software, ossia sufficiente per gli usi dell’astrofilo medio. Tutti gli eventi sono stati calcolati per le coordinate di Roma (Lat. 41° 52’ 48” N, Long. 12° 30’ 00” E) e gli orari espressi (tranne laddove altrimenti specificato) in tempo universale. 2 Almanacco Astronomico 2002 – Calendario del 2002 Calendario del 2002 January February March Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa 1 2 3 4 5 1 2 1 2 6 7 8 9 10 11 12 3 4 5 6 7 8 9 3 4 5 6 7 8 9 13 14 15 16 17 18 19 10 11 12 13 14 15 16 10 11 12 13 14 15 16 20 21 22 23 24 25 26 17 18 19 20 21 22 23 17 18 19 20 21 22 23 27 28 29 30 31 24 25 26 27 28 24 25 26 27 28 29 30 31 April May June Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa Su Mo Tu We Th Fr Sa 1 2 3 4 5 6 1 2 3 4 1 7 8 9 10 11 12 13 5 6 7 8 9 10 11 2 3 4 5 6 7 8 14 15 16 17 18 19 20 12 13 14 15 16 17 18 9 10 11 12 13 14 15 21 22 23 24 25 26 27 19 20 21 22 23 24 25 16 17 18 19 20 21 22 28 29 30 26 27 28 29 30 31 23 24 25 26 27 28 29 30 July August September Su Mo Tu We -

Saul J. Adelman
SAUL J. ADELMAN Department of Physics 1434 Fairfield Avenue The Citadel Charleston, SC 29407 Charleston, SC 29409 (843) 766-5348 (843) 953-6943 CURRENT POSITION: Professor of Physics, The Citadel (Aug. 22, 1989 - to date) PAST POSITIONS: Associate Professor of Physics, The Citadel (Aug. 23, 1983 to Aug. 21, 1989) NRC-NASA Research Associate, NASA Goddard Space Flight Center (Aug. 1, 1984 - July 31, 1986) Assistant Professor of Physics, The Citadel (Aug. 21, 1978 - Aug. 22, 1983) Assistant Professor of Astronomy, Boston University (Sept. 1, 1974 - Aug. 31, 1978) NAS/NRC Postdoctoral Resident Research Associate, NASA Goddard SpaceFlight Center (Aug. 1, 1972 - Aug. 31, 1974) EDUCATION: Ph.D. in Astronomy, California Institute of Technology, June 1972; Thesis: A Study of Twenty- One Sharp-lined Non-Variable Cool Peculiar A Stars, December 1971 (Dissertation Abstracts International 33, 543-13, number 77-22, 597) B.S. in Physics with high honors and high honors in physics, University of Maryland, June 1966 ACADEMIC HONORS: Phi Beta Kappa Phi Kappa Phi Sigma Pi Sigma Sigma Xi Summer Institute in Space Physics at Columbia University 1965 NDEA Title IV Fellowship 1966-69 ARCS Foundation Fellowship 1970-71 Citadel Development Foundation Faculty Fellowship 1987-93 Faculty Achievement Award 1989, 1997 Governor’s Award for Excellence in Scientific Research at a Primarily Undergraduate Institution 2011 OBSERVING EXPERIENCE: Guest Investigator, Dominion Astrophysical Observatory 1984-2018 Guest Investigator, Hubble Space Telescope 2003-05, 2011-18 Participant -

EKCENTRIK Goto Mount最新版本091214
EklKipse Ekcentrik Mount INSTRUCTIONS CONTENT FOR EKCENTRIK USER INTRODUCTION.................................................................................1 ALL PARTS.........................................................................................2 ASSEMBLY INSTRUCTIONS.............................................................3 FEATURES.........................................................................5 OPERATION MANUAL FOR EKSTREAM KONTROLLER 30........... 6 KEY DESCRIPTION.................................................................................6 STATUS DESCRIPTION...........................................................................6 OPERATION PROCESS...........................................................................7 POWER ON......................................................................................7 WARNING........................................................................................7 ALIGNMENT STATUS........................................................................7 CHANGE THE DATE..................................................................7 CHANGE THE TIME...................................................................8 CHANGE THE SITE...................................................................8 ALIGNMENT.............................................................................9 NAVIGATION STATUS.....................................................................11 MENU STATUS................................................................................11 -

GTO KEYPAD Version V4.19.3
ASTRO-PHYSICS GTO KEYPAD Version v4.19.3 Flash RAM Updates Keypad flash RAM updates can be accomplished through the Internet. Check our web site www.astro-physics.com periodically for further information. August 2018 CONTENTS ABOUT THIS MANUAL 5 GTO KEYPAD CONTROLLER 6 Layout and Buttons of the Keypad 6 Vacuum Fluorescent Display 6 N-S-E-W Directional Buttons 6 RA/DEC REV Button: 6 STOP Button 7 Number Buttons 7 <PREV and NEXT> Buttons 7 GoTo Button 7 ± Button 7 MENU Button 7 FOC Button 7 Retractable Hanger 7 Keypad Protector 8 Installation: 8 Keypad Care and Warranty 8 Warranty 8 Keypad Battery for 256K Memory Boards 8 Keypad Battery for 512K Memory Boards 8 Cleaning Keypad Display 8 Temperature Ratings 8 GETTING STARTED – DO THIS AT HOME, IF POSSIBLE 9 Setup your Mount and Cable Connections 9 Gather Basic Information 9 Enter Your Location, Date and Time 9 Resetting Daylight Savings and Time in the Spring and Fall 11 Setting Keypad to GMT (aka UTC) 12 Practice Using your Keypad 13 YOUR FIRST OBSERVING SESSION & FOR PORTABLE MOUNTS 14 Normal Startup Sequence for Mounts that are in the field 14 Assemble Your Mount 14 Startup sequence 14 Star Sync 14 Resume Last Position 15 New Setup → New Setup Start From Park Position (press 1, 2, 3, or 4) 15 Helpful Hints 15 AUTO-CONNECT SEQUENCE – FOR PERMANENT, POLAR-ALIGNED MOUNTS 16 Important Points 16 EXTERNAL STARTUP SEQUENCE – FOR COMPUTER CONTROLLED MOUNTS 17 Important Points 17 POLAR ALIGNMENT – WHICH METHOD TO CHOOSE? 18 N Polar Calibrate - Calibrating with Polaris 18 Two-Star Calibration 19 -

Nazwy Gwiazd Nieba Północnego O Etymologii Arabskiej
Uniwersytet Kazimierza Wielkiego Wydział Humanistyczny Instytut Neofilologii i Lingwistyki Stosowanej Nazwy gwiazd nieba północnego o etymologii arabskiej Marek Polasik nr albumu 70088 Praca licencjacka napisana pod kierunkiem dra Sebastiana Bednarowicza Bydgoszcz 2013 Kazimierz Wielki University, Bydgoszcz Institute of Modern Languages and Applied Linguistics Star names of Arabic etymology in the northern sky Marek Polasik nr 70088 Supervisor: Dr Sebastian Bednarowicz Bydgoszcz 2013 1 جامعة كازيميش فيلكي في بيدغوشج معهد اللغات الحديثة واللسنيات التطبيقية السماء العربية لنجوم السماء الشمالية Marek Polasik رقم اللبوم ٧٠٠٨٨ مشرف: الدكتور Sebastian Bednarowicz بيدغوشج ٢٠١٣ 2 n az w i sk o i i m i ę Polasik Marek nr a l b u m u 70088 k ie r u n e k s t u d i ów filologia s p e c j a l ność Lingwistyka stosowana jęz. angielski z jęz. arabskim t y p s t u d i ów i f o r m a ks z tał c e n i a I stopień, stacjonarne OŚWIADCZENIE autora/autorów pracy dyplomowej Świadomy odpowiedzialności prawnej, oświadczam, że praca dyplomowa Nazwy gwiazd nieba północnego o etymologii arabskiej została wykonana samodzielnie i nie zawiera treści uzyskanych w sposób niezgodny z obowiązującymi przepisami Oświadczam również, że przedstawiona praca nie była wcześniej przedmiotem procedur związanych z uzyskaniem tytułu zawodowego w uczelni. Oświadczam ponadto, że drukowana wersja pracy dyplomowej jest identyczna z załączoną jej wersją elektroniczną. Bydgoszcz, dn. ……………………....... …......................................... (podpis studenta) 3 Streszczenie pracy dyplomowej Temat pracy dyplomowej Nazwy gwiazd nieba północnego o etymologii arabskiej Imię i nazwisko autora pracy: Marek Polasik Nr albumu: 70088 Imię i nazwisko promotora pracy: dr Sebastian Bednarowicz Słowa kluczowe: Arabic, star, name, constellation, etymology, origin, meaning Treść streszczenia Praca ta została napisana pod wpływem inspiracji rozgwieżdżonym niebem jak i wrodzonej ciekawości do zagadek etymologicznych.