Notes on Hand Evaluation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
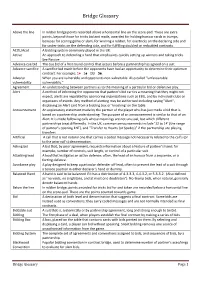
Bridge Glossary
Bridge Glossary Above the line In rubber bridge points recorded above a horizontal line on the score-pad. These are extra points, beyond those for tricks bid and made, awarded for holding honour cards in trumps, bonuses for scoring game or slam, for winning a rubber, for overtricks on the declaring side and for under-tricks on the defending side, and for fulfilling doubled or redoubled contracts. ACOL/Acol A bidding system commonly played in the UK. Active An approach to defending a hand that emphasizes quickly setting up winners and taking tricks. See Passive Advance cue bid The cue bid of a first round control that occurs before a partnership has agreed on a suit. Advance sacrifice A sacrifice bid made before the opponents have had an opportunity to determine their optimum contract. For example: 1♦ - 1♠ - Dbl - 5♠. Adverse When you are vulnerable and opponents non-vulnerable. Also called "unfavourable vulnerability vulnerability." Agreement An understanding between partners as to the meaning of a particular bid or defensive play. Alert A method of informing the opponents that partner's bid carries a meaning that they might not expect; alerts are regulated by sponsoring organizations such as EBU, and by individual clubs or organisers of events. Any method of alerting may be authorised including saying "Alert", displaying an Alert card from a bidding box or 'knocking' on the table. Announcement An explanatory statement made by the partner of the player who has just made a bid that is based on a partnership understanding. The purpose of an announcement is similar to that of an Alert. -

CONTEMPORARY BIDDING SERIES Section 1 - Fridays at 9:00 AM Section 2 – Mondays at 4:00 PM Each Session Is Approximately 90 Minutes in Length
CONTEMPORARY BIDDING SERIES Section 1 - Fridays at 9:00 AM Section 2 – Mondays at 4:00 PM Each session is approximately 90 minutes in length Understanding Contemporary Bidding (12 weeks) Background Bidding as Language Recognizing Your Philosophy and Your Style Captaincy Considering the Type of Scoring Basic Hand Evaluation and Recognizing Situations Underlying Concepts Offensive and Defensive Hands Bidding with a Passed Partner Bidding in the Real World Vulnerability Considerations Cue Bids and Doubles as Questions Free Bids Searching for Stoppers What Bids Show Stoppers and What Bids Ask? Notrump Openings: Beyond Simple Stayman Determining When (and Why) to Open Notrump When to use Stayman and When to Avoid "Garbage" Stayman Crawling Stayman Puppet Stayman Smolen Gambling 3NT What, When, How Notrump Openings: Beyond Basic Transfers Jacoby Transfer Accepting the transfer Without interference Super-acceptance After interference After you transfer Showing extra trumps Second suit Splinter Texas Transfer: When and Why? Reverses Opener’s Reverse Expected Values and Shape The “High Level” Reverse Responder’s Options Lebensohl Responder’s Reverse Expected Values and Shape Opener’s Options Common Low Level Doubles Takeout Doubles Responding to Partner’s Takeout Double Negative Doubles When and Why? Continuing Sequences More Low Level Doubles Responsive Doubles Support Doubles When to Suppress Support Doubles of Pre-Emptive Bids “Stolen Bid” or “Shadow” Doubles Balancing Why Balance? How to Balance When to Balance (and When Not) Minor Suit Openings -

Bidding Notes
Bidding Notes Paul F. Dubois February 19, 2015 CONTENTS 1 Preliminaries 6 1.1 How to Use This Book.....................................6 1.2 Casual Partners.........................................7 1.3 Acknowledgments.......................................7 1.4 Notation and Nomenclature...................................7 1.5 The Captain Concept......................................8 2 Hand Evaluation 9 2.1 Basic System..........................................9 2.1.1 Adjusting to the Auction................................ 10 2.1.2 Losing Trick Count................................... 10 2.2 Bergen Method......................................... 11 2.3 Examples............................................ 11 2.4 What Bid To Open....................................... 11 3 Reverses 13 3.1 Reverses by Opener....................................... 13 3.1.1 Responding To Opener’s Reverse........................... 13 3.2 Reverses By Responder..................................... 14 4 Opening Notrump 15 4.1 How To Choose A Response To 1N.............................. 15 4.1.1 Responding With No Major Suit Or Long Minor................... 16 4.1.2 Responding With A Major Suit Or Long Minor.................... 16 4.2 Stayman Convention...................................... 16 4.3 Major Transfers......................................... 17 4.3.1 When the transfer is doubled or overcalled...................... 18 4.3.2 Interference before transfers.............................. 19 4.4 When Responder Is 5-4 In The Majors............................ -

Professional Slam Bidding Part II
Contents Bidding space ...................................................................................... 5 Splinters ........................................................................................... 30 Agreements ....................................................................................... 48 Last train ........................................................................................... 73 Blackwood ........................................................................................ 80 Ace asking at low levels ..................................................................... 83 Conditional RKCB ............................................................................. 91 Blackwood depending on the context. .................................................. 95 When Blackwood is urgently needed. ................................................... 99 Exclusion Keycard Blackwood .......................................................... 108 Turbo .............................................................................................. 115 Pick a slam ...................................................................................... 127 Another meaning for 5NT ................................................................. 136 In the Blackwood neighborhood ........................................................ 139 Decision ......................................................................................... 148 3 4 BIDDING SPACE Preemptive bidding has a great advantage – it takes -

New Zealand Bridge Dealer West
ª © NEW ZEALAND ¨ § BRIDGE ONLINE A truly international Kiwi. Read about a New Zealander who has made a big difference April 2014 Volume 50 No 2 in our bridge world ... Page 10 Editorial Welcome to the world of digital ... and find out some really good news from 4 Howick and The Bay of Plenty. For Intermediates ... Do you know declarer's shape ... their hand shape, of course!? 24 For new players Your first bridge steps Are you a good partner? 21 Tracey Lewis looks at what makes a good partner ... and partnership. Curly Shirl's Tips What are the three Cs which you should apply to every hand you play or defend? 19 Shirley reveals. Tournaments are fun even if you are new to the game. Find out why ... 20 70 years together and still smiling Find out more ... 23 Try a Bridge Quiz Have you heard of Sam Stayman? That's not one of the questions but there is a question 22 about him. Read on ... Regional round-up All kinds of news, stories and achievements from around the country. ...even the odd bridge hand ... on a bridge club wall. Where's that? 25 Board news and views They administer our game, our sport. Who are they and what are they thinking and doing for us? Read on ... 54 Tournament News Top Performance at The Gold Coast Read how Michael Ware and GeO Tislevoll (with a little help from 7 their teammates) won the Gold Coast Teams. Tournament Results and Recent High Scores Maybe you have done well recently at a tournament? Your name maybe mentioned. -

2004 Bridge Bulletin Index
2004 Bridge Bulletin Index ACBL BRIDGE HALL OF FAME. 2004 inductees named: Amalya Kearse, Jeff Rubens, Harold “Harry” Harkavy and Merwyn “Jimmy” Maier (Feb). Weichsel chosen for Hall of Fame (Apr). Nominations open for 2005 class (Jul, Aug, Sep). ACBL BOARD OF DIRECTORS. Minutes from the Fall 2003 meeting in New Orleans (May). Election notices (Mar, Apr, May). Reno Spring 2004 minutes (Jun). New York Summer 2004 minutes; Treasurer’s report; By-laws (Oct). Election results (Dec). ACBL CHARITY FOUNDATION. Alzheimer’s Association is 2004 grant recipient (Feb). 2004 Charity Committee appointments named (Mar). Election deadlines (Jul). District grants announced for 2005 (Nov). ACBL CHARITY GAME. Winners (Mar, Jul). ACBL CLUB DIRECTOR AND CLUB DIRECTOR UPDATE COURSES. Monthly lists. ACBL EDUCATIONAL FOUNDATION. Promotion (Jan, Mar, May, Jul, Sep). Election news (Aug). ACBL 49ER PAIRS. Winners (Jan). ACBL GOODWILL COMMITTEE. Kay Teal named 2004 Goodwill Member of the Year; 2004 Goodwill Committee appointments named (Mar). ACBL HONORARY MEMBER OF THE YEAR. Sidney Lazard named 2004 recipient (Jan). ACBL INSTANT MATCHPOINT GAME. Promotion (Jul, Aug, Sep). Winners (Dec). ACBL INTERNATIONAL FUND GAME. Winners (Jun, Oct, Nov). ACBL PATRON MEMBER LIST. Dec. ACBL PRESIDENT. Interview with 2004 president Bruce Reeve (Jan). ACBL TEACHER ACCREDITATION PROGRAM (TAP) SEMINARS. Monthly list. ACBL-WIDE SENIOR PAIRS. Winners (Oct.) ACE OF CLUBS. Winners of the annual masterpoint races (Apr). ADVANCED PLAYERS SECTION. Columnists Eric Kokish, Larry Cohen, Eddie Kantar, Mike Lawrence, Frank Stewart and Karen Walker. See also individual columnist listings. AMERICAN BRIDGE ASSOCIATION. Schedule of upcoming national events — monthly in Schedule of Events. AS I SEE IT. -

HAND EVALUATION & REVALUING by BARBARA SEAGRAM
HAND EVALUATION & REVALUING by BARBARA SEAGRAM Many students have great difficulty with the concept of hand evaluation. I believe that it is right to count distribution even as an opening bidder. Most people now count long suits (1 point for 5th card in long suit and 1 extra point for 6th etc:) That is counting distribution. You need 13 points including distribution to open the bidding in 1st or 2nd seat. Some books say 12 only but then they are not including distribution. You need to know the Rule of 20 for when you are in 1st or 2nd seat and only have 11 or 12 points. If you find yourself close to an opening bid but feel you don’t have enough points to open, use the Rule of 20. Count your HCP and then add the length of the two longest suits. If this totals 20, then you have permission to open the bidding. e.g. If you have S Axxx H Axxx D Axxx C x = 12 HCP plus two four card suits = 20. Now you have permission to open the bidding. Let’s call points including distribution: TOTAL POINTS. NOTE: You should not use the Rule of 20 to give you permission to open the bidding when you have a hand such as this: S Qx H KJx D KQxx C Jxxx This assortment of junk will tally 20 with Rule of 20 but doubleton Queens or Jacks are a sorry sight and do not deserve much respect. We call Queens and Jacks “Quacks!” This should not be an opening bid. -

Defensive Bidding Release 7.0
Defensive Bidding Release 7.0 Paul F. Dubois Jul 31, 2021 TABLE OF CONTENTS 1 Preliminaries 1 1.1 Topics Covered.........................................1 2 Notrump Defenses 2 2.1 Landy..............................................2 2.2 Meckwell............................................2 2.3 Modified Cappelletti......................................2 2.4 Bloomen............................................3 2.5 Woolsey............................................3 2.5.1 Defenses to Woolsey.................................3 2.6 Mohan.............................................3 3 Runouts 5 3.1 Introduction to Runouts....................................5 3.1.1 Use The Runout Over Conventional Doubles?....................5 3.2 Meckwell Escapes.......................................5 3.3 The Handy Runout.......................................6 3.3.1 Direct Seat Doubles..................................6 3.3.2 Fourth Seat Doubles.................................6 3.4 Guoba.............................................7 3.4.1 Direct Seat Doubles..................................7 3.4.2 Fourth Seat Doubles.................................7 3.5 Escape From Moscow, or D.O.N.T...............................7 4 Two-Suited Competitive Bids8 4.1 Sandwich 1N..........................................8 4.2 Extended Michaels.......................................8 4.3 Top and Bottom Cue Bid....................................9 5 Special Doubles 10 5.1 Support Doubles and Redoubles................................ 10 5.2 Responsive Doubles..................................... -

Are Counted. the Presence of a 5-Card Suit Is Worth One Point, and the Presence of Tens Can Also Be Taken Into Account
- 1 - INTERMEDIATE-2 BRIDGE LESSON 1 NO TRUMP BIDDING General Considerations: a. Strength - High cards points only (never distribution) are counted. The presence of a 5-card suit is worth one point, and the presence of tens can also be taken into account. The system is based upon 26 HCP's = Game, 34 HCP's = Small Slam, and 37 HCP's = Grand Slam. b. Distribution - Only balanced hands; i.e., no voids, no singletons, and not more than one doubleton, qualify. (Examples: 4-3-3-3, 4-4-3-2, 5-3-3-2) (1) The 5-card suit is rarely a Major suit. (2) Distributional exception: (5-4-2-2) Where the two doubletons are Major suits headed by an Ace or a King (Example: KX AX KJXX AQXXX). c. Location Of Strength - The concentration of honors, presence of any tenaces (AQ, KJ, etc.), or the holding of a worthless doubleton are rarely considered. OPENING NO TRUMP BIDS a. 0-12 HCP’s - Pass b. 13-14 HCP's - Bid one of a preferred Minor and rebid 1NT c. 15-17 HCP’s - Bid 1NT d. 18-20 HCP’s - Open one of a Minor and jump to 2NT with 18 or 19 HCP’s & 3NT with 20 HCP’s e. 21-22 HCP's - Open 2NT f. 23-24 HCP’s - Open “2C”(Strong, Artificial, and Forcing) and rebid 2NT q. 25-27 HCP's - Open "2C" (Strong, Artificial, and Forcing) and jump to 3NT h. Gambling "3NT" - Holding a 7-Card self-sufficient Minor suit (Example: AKQXXXX ) If partner has stoppers in both Majors and two (2) quick tricks or better, he/she passes. -

Australian Bridge Federation Inc
NEWSLETTER AUSTRALIAN BRIDGE FEDERATION INC. Editor: Barbara Travis ([email protected]) No. 191 June 2018 Approved for Print Post S65001/00163 ABN 70 053 651 666 WBF PRESIDENT RONA ON WORLD CHAMPIONSHIPS, CHEATS AND THE FUTURE President of the World Bridge Federation (WBF) since 2009, Gianarrigo Rona is one of the most influential and visible people in the bridge world. On a sunny February morning in the Gold Coast, I sit down with President Rona to hear his thoughts on topics ranging from the Olympic movement and the cheating scandal through to youth bridge and the future of the game. This is not Rona’s first visit to Australia. This time, Rona has come at the invitation of the organiser of the 5th Commonwealth Nations Bridge Competition. While in Australia, he will also be continuing negotiations with Bruce Neill, President of the Australian Bridge Federation, about Australia potentially hosting a future WBF world championship. Mr Gianarrigo Rona being interviewed by Liam Milne Recently, the WBF has come under fire for various reasons. These have included accusations of being slow to investigate government support and subsidies for bridge in this region. and act against cheats, allowing Poland to contest (and win) Rona points out that aside from bridge, many other activities the 2015 Bermuda Bowl despite two of its players having still strive to be accepted by the International Olympic their invitations to play withdrawn, as well as the scoring Committee. Surely this must mean it is worth something to be scandal of 2016 where the World Bridge Games Open Pairs part of the Olympic movement, otherwise why would they be and Women’s Pairs gold medals were each awarded to the trying to get in? He also claims that the benefits go beyond ‘wrong pair’ before scoring errors were discovered. -

BULLETIN the Master Point Press IBPA Book of the Year Shortlist
THE INTERNATIONAL BRIDGE PRESS ASSOCIATION Editor: John Carruthers This Bulletin is published monthly and circulated to members of the International Bridge Press Association, comprising the world’s leading journalists, authors and editors of news, books and articles about contract bridge, with an estimated readership of some BULLETIN 200 million people who enjoy the most widely-played of all card games. www.ibpa.com Bulletin No. 642 July 10, 2018 President Barry Rigal (USA) +1 212 366 4799 [email protected] Chairman Per Jannersten (Sweden) [email protected] The Master Point Press IBPA Executive Vice-President Book of the Year Shortlist David Stern (Australia) We have five terrific candidates for Book of the Year. As usual, the hopefuls are [email protected] a varied bunch, with teaching experts and intermediates the main theme. Only Organizational one of the five could be considered pure entertainment. Here they are: Vice-President & Augie Boehm, Expert Hand Evaluation, 2017, 142 pp, Bulletin Production paperback, $14.95 Manager If bidding were as simple as counting high-card points, most of us would have Dilip Gidwani (India) lost interest in bridge a long time ago. Appreciating the life-long challenge of a +91 98214 53817 game immune to mastery, experts are always trying to hone their bidding [email protected] judgment. This book’s aim is to help you develop good bidding judgment by Secretary refining and improving your hand evaluation, which is the bedrock of good Elisabeth van Ettinger bidding. Learning the requirements for everyday sequences suffices to solve a (Netherlands) great many situations – but often not when a borderline hand falls into the +31 655 680 120 gray zone. -

Newsletter Australian Bridge Federation Inc
NEWSLETTER AUSTRALIAN BRIDGE FEDERATION INC. Editor: [email protected] No. 186 July 2017 Approved for Print Post S65001/00163 ABN 70 053 651 666 THE AUSTRALIAN TEAMS IN SEOUL OPEN TEAM SENIORS’ 2 TEAM Following the Asia Pacific Bridge Peter Gill – Andrew Peake Jonathon Free – George Smolanko Federation Championships, there were Peter Hollands – Justin Mill Simon Hinge – Robbie van Riel Playoffs to determine the Asian teams David Beauchamp – Matthew Thomson Andy Braithwaite – Arjuna de Livera to represent their Zone at the World Ben Thompson (NPC) 1st China 394.08 Championships in Lyon in August. Simultaneously, the Australian Open 1st China 376.69 VPs 6th Australia 1 341.36 and Women’s Teams held their Zonal 7th Australia 345.30 8th Australia 2 312.62 matches against New Zealand, and there were Open and Youth Pairs WOMEN’S TEAM JUNIOR TEAM Championships. Marianne Bookallil – Jodi Tutty Charles McMahon – John McMahon Margaret Bourke – Sue Lusk Matt Smith – Jamie Thompson AUSTRALIAN OPEN 109 Candice Ginsberg – Barbara Travis Christopher Rhodes – Nico Ranson lost to Peter Reynolds (NPC) John Newman (NPC) NEW ZEALAND OPEN 117 Liam Milne (Coach) 1st China 344.94 AUSTRALIAN WOMEN 150 4th Australia 280.26 1st China 395.46 defeated 5th Australia 293.36 NEW ZEALAND WOMEN 66 SENIORS’ 1 TEAM OPEN PAIRS Pauline Gumby – Warren Lazer GIRLS’ TEAM 2nd Pauline Gumby - Warren Lazer Avi Kanetkar – Bruce Neill Ailsa Peacock – Lakshmi Sunderasan – Peter Buchen – Terry Brown Kirstyn Fuller BUTLER PAIRS George Bilski (NPC) Renee Cooper – Francesca McGrath 1st Jamie Thompson - Matt Smith Christy Geromboux (NPC) Liam Milne (Coach) 1st China 234.93 4th Australia 147.02 INSIDE THIS EDITION PRESIDENT’S REPORT by Bruce Neill Feature Stories I have just returned from the Asia Pacific Bridge (APBF) Autumn Nationals 6 Championships in Seoul.