The Dynamics of a Viscous Soap Film with Soluble Surfactant Jean-Marc Chomaz
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Pernille Fischer Christensen
A FAMILY EEN FILM VAN Pernille Fischer Christensen WILD BUNCH HAARLEMMERDIJK 159 - 1013 KH – AMSTERDAM WWW.WILDBUNCH.NL [email protected] WILDBUNCHblx A FAMILY – Pernille Fischer Christensen PROJECT SUMMARY Een productie van ZENTROPA Taal DEENS Originele titel EN FAMILIE Lengte 99 MINUTEN Genre DRAMA Land van herkomst DENEMARKEN Filmmaker PERNILLE FISCHER CHRISTENSEN Hoofdrollen LENE MARIA CHRISTENSEN (Brothers, Terribly Happy) JESPER CHRISTENSEN (Melancholia, The Young Victoria, The Interpreter) PILOU AESBAK (Worlds Apart) ANNE LOUISE HASSING Release datum 4 AUGUSTUS 2011 DVD Release 5 JANUARI 2012 Awards/nominaties FILM FESTIVAL BERLIJN 2010 NOMINATIE GOUDEN BEER WINNAAR FIPRESCI PRIJS Kijkwijzer SYNOPSIS Ditte Rheinwald vertegenwoordigt de jongste generatie van de beroemde Deense bakkersfamilie. Haar eigen dromen en ambities zijn echter anders dan die van haar familie. Als ze een droombaan bij een galerie in New York krijgt aangeboden, besluit ze samen met haar vriend Peter de kans aan te grijpen. De toekomst lijkt stralend, het leven vrolijk en simpel. Maar dan wordt Ditte’s charismatische vader Rikard, meesterbakker en hofleverancier, ernstig ziek. Als Rikard eist dat zij de leiding overneemt van het familiebedrijf, raakt haar hele leven uit balans. Plotseling is het leven niet meer zo simpel. CAST Ditte Lene Maria Christensen Far Jesper Christensen Peter Pilou Asbæk Sanne Anne Louise Hassing Chrisser Line Kruse Line Coco Hjardemaal Vimmer Gustav Fischer Kjærulff CREW DIRECTOR Pernille Fischer Christensen SCREENWRITERS Kim Fupz -
![BROTHERHOOD [Broderskab]](https://docslib.b-cdn.net/cover/8282/brotherhood-broderskab-608282.webp)
BROTHERHOOD [Broderskab]
Presents A FILM BY NICOLO DONATO BROTHERHOOD [Broderskab] STARRING THURE LINDHARDT DAVID DENCIK NICOLAS BRO MORTEN HOLST Country of Origin: Denmark / In Danish with English Subtitles Running time: 90 minutes Shot On: RED1 Sound: Dolby SR Digital Screen Ratio: 1:2:35 Rating: Not Rated PRESS CONTACT SASHA BERMAN SHOTWELL MEDIA TEL: 310.450.5571 [email protected] Please download photos from our website: www.olivefilms.com New York Premiere August 6, 2010 SYNOPSIS When Lars (Thure Lindhardt) is cheated out of promotion to sergeant following rumors about his unbecoming behavior towards some of his men, he decides to leave the army. Back home, his overly proper suburban parents succeed in driving him nuts in record time, as they do everything in their power to sweep the embarrassing incident under the carpet. By chance, Lars runs into a small radical group of neo-Nazis led by the charismatic Michael ‘Fatso’ (Nicolas Bro). Initially, Lars distances himself from their ideology and methods, but fuelled by defiance against the system in general – and his parents in particular – Lars decides to join the group. Fatso immediately spots the potential in the intelligent eloquent Lars, even though his right-hand man, Jimmy (David Dencik), does not agree. Lars rapidly advances through the ranks and is nominated as an A member, despite the fact that this promotion should really have gone to Jimmy’s younger brother, Patrick (Morten Holst). Lars moves out of his parents’ house and into board chairman Ebbe’s remotely situated summer cottage, which Jimmy is in the process of renovating. Despite their initial dislike of each other, the attraction between the two men soon becomes too strong to ignore, and even though they feel torn between ideology and emotions, they begin a secret relationship. -

GUIDELINES for WRITING SOAP NOTES and HISTORY and PHYSICALS
GUIDELINES FOR WRITING SOAP NOTES and HISTORY AND PHYSICALS by Lois E. Brenneman, M.S.N, C.S., A.N.P, F.N.P. © 2001 NPCEU Inc. all rights reserved NPCEU INC. PO Box 246 Glen Gardner, NJ 08826 908-537-9767 - FAX 908-537-6409 www.npceu.com Copyright © 2001 NPCEU Inc. All rights reserved No part of this book may be reproduced in any manner whatever, including information storage, or retrieval, in whole or in part (except for brief quotations in critical articles or reviews), without written permission of the publisher: NPCEU, Inc. PO Box 246, Glen Gardner, NJ 08826 908-527-9767, Fax 908-527-6409. Bulk Purchase Discounts. For discounts on orders of 20 copies or more, please fax the number above or write the address above. Please state if you are a non-profit organization and the number of copies you are interested in purchasing. 2 GUIDELINES FOR WRITING SOAP NOTES and HISTORY AND PHYSICALS Lois E. Brenneman, M.S.N., C.S., A.N.P., F.N.P. Written documentation for clinical management of patients within health care settings usually include one or more of the following components. - Problem Statement (Chief Complaint) - Subjective (History) - Objective (Physical Exam/Diagnostics) - Assessment (Diagnoses) - Plan (Orders) - Rationale (Clinical Decision Making) Expertise and quality in clinical write-ups is somewhat of an art-form which develops over time as the student/practitioner gains practice and professional experience. In general, students are encouraged to review patient charts, reading as many H/Ps, progress notes and consult reports, as possible. In so doing, one gains insight into a variety of writing styles and methods of conveying clinical information. -

The Life of a Surface Bubble
molecules Review The Life of a Surface Bubble Jonas Miguet 1,†, Florence Rouyer 2,† and Emmanuelle Rio 3,*,† 1 TIPS C.P.165/67, Université Libre de Bruxelles, Av. F. Roosevelt 50, 1050 Brussels, Belgium; [email protected] 2 Laboratoire Navier, Université Gustave Eiffel, Ecole des Ponts, CNRS, 77454 Marne-la-Vallée, France; fl[email protected] 3 Laboratoire de Physique des Solides, CNRS, Université Paris-Saclay, 91405 Orsay, France * Correspondence: [email protected]; Tel.: +33-1691-569-60 † These authors contributed equally to this work. Abstract: Surface bubbles are present in many industrial processes and in nature, as well as in carbon- ated beverages. They have motivated many theoretical, numerical and experimental works. This paper presents the current knowledge on the physics of surface bubbles lifetime and shows the diversity of mechanisms at play that depend on the properties of the bath, the interfaces and the ambient air. In particular, we explore the role of drainage and evaporation on film thinning. We highlight the existence of two different scenarios depending on whether the cap film ruptures at large or small thickness compared to the thickness at which van der Waals interaction come in to play. Keywords: bubble; film; drainage; evaporation; lifetime 1. Introduction Bubbles have attracted much attention in the past for several reasons. First, their ephemeral Citation: Miguet, J.; Rouyer, F.; nature commonly awakes children’s interest and amusement. Their visual appeal has raised Rio, E. The Life of a Surface Bubble. interest in painting [1], in graphism [2] or in living art. -

Submarino / Berlinale Competition a Family/ Berlinale Competition Super
vINTErBErG rETUrNS To rEALISM family entanglements ADMIratioN For THE oUTSIDEr The director of Festen/The Celebration, Thomas Berlin winner for A Soap, Pernille Fischer Christensen This tagline could well describe the spirit of the stories Vinterberg brings his latest filmSubmarino to the is back competing at the Berlinale with A Family. At the in the five films chosen by Berlinale’s Generation: Birger Berlinale Competition. A story about two estranged heart of the story about family ties is the relationship Larsen’s Super Brother and four short films,Megaheavy, brothers marked by an early tragedy. between a father and his daughter. Out of Love, Sun Shine and Whistleless. PAGE 3 PAGE 6 PAGE 9 & 15-20 FILM IS PUBLISHED BY #THE DANISH FILM68 INSTITUTE / febuarY 2010 submarino / Berlinale competition a family / Berlinale competition super brother / Berlinale Generation megaheavy / out of love / sun shine / whistleless / Generation short films PAGE 2 / FILM#68 / BERLIN ISSUE FILM#68/ BERLIN issue insiDe vINTErBErG rETUrNS To rEALISM FAMILY ENTANGLEMENTS ADMIrATIoN For THE oUTSIDEr ESSENTIAL BoNDS / BErLINALE CoMPETITIoN The director of Festen/The Celebration, Thomas Berlin winner for A Soap, Pernille Fischer Christensen This tagline could well describe the spirit of the stories Vinterberg brings his latest filmSubmarino to the is back competing at the Berlinale with A Family. At the in the five films chosen by Berlinale’s Generation: Birger Berlinale Competition. A story about two estranged heart of the story about family ties is the relationship Larsen’s Super Brother and four short films,Megaheavy, brothers marked by an early tragedy. between a father and his daughter. -

Paradox Presents a Film by Hans Petter Moland
PARADOX PRESENTS STELLAN SKARSGÅRD BRUNO GANZ PÅL SVERRE HAGEN A FILM BY HANS PETTER MOLAND 02 PRESSBOOK IN ORDER OF DISAPPEARANCE PARADOX FILM & TRUSTNORDISK PRESENT (KRAFTIDIOTEN) ACTION COMEDY, NORWAY/SWEDEN/DENMARK 2014 A FILM BY HANS PETTER MOLAND WITH STELLAN SKARSGÅRD, BRUNO GANZ, PÅL SVERRE HAGEN, BIRGITTE HJORT SØRENSEN, JAKOB OFTEBRO, KRISTOFFER HIVJU, ANDERS BAASMO CHRISTIANSEN WORLD PREMIERE IN BERLINALE COMPETITION, FEBRUARY 10TH SOUND 5.1, FORMAT DCP 2K, SCREEN RATIO 1:2,39 04 PRESSBOOK IN ORDER OF DISAPPEARANCE SYNOPSIS Nils snow ploughs the wild winter mountains of Norway, and is recently awarded Citizen of the Year. When his son is murdered for something he did not do, Nils wants revenge. And justice. His actions ignites a war between the vegan gangster “The Count“ and the Serbian mafia boss “Papa“. Winning a blood feud isn´t easy. Especially not in a welfare state. But Nils has something going for him: Heavy machinery and beginner‘s luck. PRESSBOOK IN ORDER OF DISAPPEARANCE 05 06 PRESSBOOK IN ORDER OF DISAPPEARANCE DIRECTOR: HANS PETTER MOLAND Hans Petter Moland never repeats himself. His films are eclectic and His adaptation of the famous Norwegian book, COMRADE PEDER- unique, and he explores both tragedy and – this time – comedy. SEN (2006) won him the award for Best Direction at the Montre- al World Film Festival, and his short film UNITED WE STAND won IN ORDER OF DISAPPEARANCE is Hans Petter Molands third Grand Prix in Clairmont Ferrand and an additional 23 awards world- Competition entry in the Berlinale. His last feature, A SOMEWHAT wide. GENTLE MAN won the Berliner Morgenpost Readers‘ Award at the Berlinale in 2010 and numerous prizes, including the Special Jury Moland has also won all major commercial film awards, including Prize at Chicago International Film Festival and a Norwegian Amanda Gold Lions in Cannes and Clio Awards, and he has directed a play for Best Actor. -

On the Shape of Giant Soap Bubbles
On the shape of giant soap bubbles Caroline Cohena,1, Baptiste Darbois Texiera,1, Etienne Reyssatb,2, Jacco H. Snoeijerc,d,e, David Quer´ e´ b, and Christophe Claneta aLaboratoire d’Hydrodynamique de l’X, UMR 7646 CNRS, Ecole´ Polytechnique, 91128 Palaiseau Cedex, France; bLaboratoire de Physique et Mecanique´ des Milieux Het´ erog´ enes` (PMMH), UMR 7636 du CNRS, ESPCI Paris/Paris Sciences et Lettres (PSL) Research University/Sorbonne Universites/Universit´ e´ Paris Diderot, 75005 Paris, France; cPhysics of Fluids Group, University of Twente, 7500 AE Enschede, The Netherlands; dMESA+ Institute for Nanotechnology, University of Twente, 7500 AE Enschede, The Netherlands; and eDepartment of Applied Physics, Eindhoven University of Technology, 5600 MB, Eindhoven, The Netherlands Edited by David A. Weitz, Harvard University, Cambridge, MA, and approved January 19, 2017 (received for review October 14, 2016) We study the effect of gravity on giant soap bubbles and show The experimental setup dedicated to the study of such large 2 that it becomes dominant above the critical size ` = a =e0, where bubbles is presented in Experimental Setup, before information p e0 is the mean thickness of the soap film and a = γb/ρg is the on Experimental Results and Model. The discussion on the asymp- capillary length (γb stands for vapor–liquid surface tension, and ρ totic shape and the analogy with inflated structures is presented stands for the liquid density). We first show experimentally that in Analogy with Inflatable Structures. large soap bubbles do not retain a spherical shape but flatten when increasing their size. A theoretical model is then developed Experimental Setup to account for this effect, predicting the shape based on mechan- The soap solution is prepared by mixing two volumes of Dreft© ical equilibrium. -

Soap Films: Statics and Dynamics
Soap Films: Statics and Dynamics Frederik Brasz January 8, 2010 1 Introduction Soap films and bubbles have long fascinated humans with their beauty. The study of soap films is believed to have started around the time of Leonardo da Vinci. Since then, research has proceeded in two distinct directions. On the one hand were the mathematicians, who were concerned with finding the shapes of these surfaces by minimizing their area, given some boundary. On the other hand, physical scientists were trying to understand the properties of soap films and bubbles, from the macroscopic behavior down to the molecular description. A crude way to categorize these two approaches is to call the mathematical shape- finding approach \statics" and the physical approach \dynamics", although there are certainly problems involving static soap films that require a physical description. This is my implication in this paper when I divide the discussion into statics and dynamics. In the statics section, the thickness of the film, concentration of surfactants, and gravity will all be quickly neglected, as the equilibrium shape of the surface becomes the only matter of importance. I will explain why for a soap film enclosing no volume, the mean curvature must everywhere be equal to zero, and why this is equivalent to the area of the film being minimized. For future reference, a minimal surface is defined as a two-dimensional surface with mean curvature equal to zero, so in general soap films take the shape of minimal surfaces. Carrying out the area minimization of a film using the Euler-Lagrange equation will result in a nonlinear partial differential equation known as Lagrange's Equation, which all minimal surfaces must satisfy. -
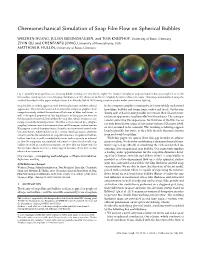
Chemomechanical Simulation of Soap Film Flow on Spherical Bubbles
Chemomechanical Simulation of Soap Film Flow on Spherical Bubbles WEIZHEN HUANG, JULIAN ISERINGHAUSEN, and TOM KNEIPHOF, University of Bonn, Germany ZIYIN QU and CHENFANFU JIANG, University of Pennsylvania, USA MATTHIAS B. HULLIN, University of Bonn, Germany Fig. 1. Spatially varying iridescence of a soap bubble evolving over time (left to right). The complex interplay of soap and water induces a complex flowonthe film surface, resulting in an ever changing distribution of film thickness and hence a highly dynamic iridescent texture. This image was simulated using the method described in this paper, and path-traced in Mitsuba [Jakob 2010] using a custom shader under environment lighting. Soap bubbles are widely appreciated for their fragile nature and their colorful In the computer graphics community, it is now widely understood appearance. The natural sciences and, in extension, computer graphics, have how films, bubbles and foams form, evolve and break. On the ren- comprehensively studied the mechanical behavior of films and foams, as dering side, it has become possible to recreate their characteristic well as the optical properties of thin liquid layers. In this paper, we focus on iridescent appearance in physically based renderers. The main pa- the dynamics of material flow within the soap film, which results in fasci- rameter governing this appearance, the thickness of the film, has so nating, extremely detailed patterns. This flow is characterized by a complex far only been driven using ad-hoc noise textures [Glassner 2000], coupling between surfactant concentration and Marangoni surface tension. We propose a novel chemomechanical simulation framework rooted in lu- or was assumed to be constant. -

Movies and Mental Illness Using Films to Understand Psychopathology 3Rd Revised and Expanded Edition 2010, Xii + 340 Pages ISBN: 978-0-88937-371-6, US $49.00
New Resources for Clinicians Visit www.hogrefe.com for • Free sample chapters • Full tables of contents • Secure online ordering • Examination copies for teachers • Many other titles available Danny Wedding, Mary Ann Boyd, Ryan M. Niemiec NEW EDITION! Movies and Mental Illness Using Films to Understand Psychopathology 3rd revised and expanded edition 2010, xii + 340 pages ISBN: 978-0-88937-371-6, US $49.00 The popular and critically acclaimed teaching tool - movies as an aid to learning about mental illness - has just got even better! Now with even more practical features and expanded contents: full film index, “Authors’ Picks”, sample syllabus, more international films. Films are a powerful medium for teaching students of psychology, social work, medicine, nursing, counseling, and even literature or media studies about mental illness and psychopathology. Movies and Mental Illness, now available in an updated edition, has established a great reputation as an enjoyable and highly memorable supplementary teaching tool for abnormal psychology classes. Written by experienced clinicians and teachers, who are themselves movie aficionados, this book is superb not just for psychology or media studies classes, but also for anyone interested in the portrayal of mental health issues in movies. The core clinical chapters each use a fabricated case history and Mini-Mental State Examination along with synopses and scenes from one or two specific, often well-known “A classic resource and an authoritative guide… Like the very movies it films to explain, teach, and encourage discussion recommends, [this book] is a powerful medium for teaching students, about the most important disorders encountered in engaging patients, and educating the public. -

THE GEOMETRY of BUBBLES and FOAMS University of Illinois Department of Mathematics Urbana, IL, USA 61801-2975 Abstract. We Consi
THE GEOMETRY OF BUBBLES AND FOAMS JOHN M. SULLIVAN University of Illinois Department of Mathematics Urbana, IL, USA 61801-2975 Abstract. We consider mathematical models of bubbles, foams and froths, as collections of surfaces which minimize area under volume constraints. The resulting surfaces have constant mean curvature and an invariant notion of equilibrium forces. The possible singularities are described by Plateau's rules; this means that combinatorially a foam is dual to some triangulation of space. We examine certain restrictions on the combina- torics of triangulations and some useful ways to construct triangulations. Finally, we examine particular structures, like the family of tetrahedrally close-packed structures. These include the one used by Weaire and Phelan in their counterexample to the Kelvin conjecture, and they all seem useful for generating good equal-volume foams. 1. Introduction This survey records, and expands on, the material presented in the author's series of two lectures on \The Mathematics of Soap Films" at the NATO School on Foams (Cargese, May 1997). The first lecture discussed the dif- ferential geometry of constant mean curvature surfaces, while the second covered the combinatorics of foams. Soap films, bubble clusters, and foams and froths can be modeled math- ematically as collections of surfaces which minimize their surface area sub- ject to volume constraints. Each surface in such a solution has constant mean curvature, and is thus called a cmc surface. In Section 2 we examine a more general class of variational problems for surfaces, and then concen- trate on cmc surfaces. Section 3 describes the balancing of forces within a cmc surface. -

Changing Europe – the Power of Dialogue
Changing Europe – The Power of Dialogue 6 –12 October 2019, Potsdam Changing Europe – The Power of Dialogue 6 –12 October 2019, Potsdam hosted by supported by 2 Changing Europe – The Power of Dialogue In a world that is faster, more complicated and fragmented than ever, it is easy to only speak and never listen, to only tweet and never talk. Pressures of pace and finance are mounting. So it is more important than ever to have strong public service media that provide quality journalism that goes out of its way to be a trusted guide, to bring people together and set a tone that enables dialogue. PRIX EUROPA is ALL about dialogue: Come together from all corners of the continent to exchange views, to see/listen for yourself together with the others, to talk and discuss, to meet and be constructive, rather than judgmental or clever. Grab the opportunity to get into conversation, to change perspective, to challenge your opinions and take away inspiration, a shared experience and new ideas. Cilla Benkö PRIX EUROPA President Director General Sveriges Radio – SR 3 Changing Europe – The Power of Dialogue Dear friends and colleagues, PRIX EUROPA is dedicated to the ideal of a united Europe, which commits itself to democratic, ethical and cultural values. This ideal is, however, in acute danger. We have to dread being abruptly pulled out of a dream that we have been living for over six decades. Of all countries, the Mother of all Democracies, the United Kingdom, is separating itself from our community. Over our Europe of togetherness, that so many people envy us for, the threat of disaster is looming.