Stony Brook University
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Neutron Stars
Neutron Stars James Lattimer [email protected] Department of Physics & Astronomy Stony Brook University J.M. Lattimer, Open Nights, 9/7/2007 – p.1/25 Pulsars: The Early History 1932 Chadwick discovers the neutron. 1934 W. Baade and F. Zwicky predict existence of neutron stars as end products of supernovae. 1939 Oppenheimer and Volkoff predict upper mass limit of neutron star. 1964 Hoyle, Narlikar and Wheeler predict neutron stars rapidly rotate. 1964 Prediction that neutron stars have intense magnetic fields. 1966 Colgate and White suggest supernovae make neutron stars. 1966 Wheeler predicts Crab nebula powered by rotating neutron star. 1967 Pacini makes first pulsar model. 1967 C. Schisler discovers a dozen pulsing radio sources, including the Crab pulsar, using secret military radar in Alaska. 1967 Hewish, Bell, Pilkington, Scott and Collins discover the pulsar PSR 1919+21, Aug 6. 1968 Pulsar discovered in Crab Nebula, and it was found to be slowing down, ruling out binary models. This also clinched their connection with Type II supernovae. 1968 T. Gold identifies pulsars with magnetized, rotating neutron stars. 1968 The term “pulsar” first appears in print, in the Daily Telegraph. 1969 “Glitches” provide evidence for superfluidity in neutron star. 1971 Accretion powered X-ray pulsar discovered by Uhuru (not the Lt.). J.M. Lattimer, Open Nights, 9/7/2007 – p.2/25 Pulsars: Later Discoveries 1974 Hewish awarded Nobel Prize (but Jocelyn Bell Burnell was not). 1974 Binary pulsar PSR 1913+16 discovered by Hulse and Taylor. It shows the orbital decay due to gravitational radiation predicted by Einstein’s General Theory of Relativity. -

David Norman Schramm October 25, 1945–December 19, 1997
NATIONAL ACADEMY OF SCIENCES D AVID NORMAN SCHRAMM 1 9 4 5 — 1 9 9 7 A Biographical Memoir by M I C H A E L S . T URNER Any opinions expressed in this memoir are those of the author and do not necessarily reflect the views of the National Academy of Sciences. Biographical Memoir COPYRIGHT 2009 NATIONAL ACADEMY OF SCIENCES WASHINGTON, D.C. DAVID NORMAN SCHRAMM October 25, 1945–December 19, 1997 B Y MICHAEL S . TURNER “ E LIVED LARGE IN ALL DIMENSIONS.” That is how Leon HLederman began his eulogy of David N. Schramm at a memorial service held in Aspen, Colorado, in December 1997. His large presence in space went beyond his 6-foot, 4-inch, 240-pound frame and bright red hair. In spite of his tragic death in a plane crash at age 52, Schramm lived large in the time dimension, too. At 18, he was married, a father, and a freshman physics major at MIT. After receiving his Ph.D. in physics from Caltech at 25, Schramm joined the faculty at the University of Texas at Austin. He left for Chicago two years later, and became the chair of the Astronomy and Astrophysics Department at the University of Chicago at age 2. He was elected to the National Academy of Sciences in 1986 at 40, became chair of the National Research Council’s Board on Physics and Astronomy at 47, and two years later became vice president for research at Chicago. He also had time for mountain climbing, summiting the highest peaks in five of the seven continents (missing Asia and Antarctica), driving a red Porsche with license plates that read “Big Bang,” and flying—owning four airplanes over his 12-year flying career and logging hundreds of hours annually. -

Neutron Star Mass and Radius Measurements
universe Communication Neutron Star Mass and Radius Measurements James M. Lattimer Department of Physics & Astronomy, Stony Brook University, Stony Brook, NY 11794-3800, USA; [email protected] Received: 24 May 2019; Accepted: 21 June 2019; Published: 28 June 2019 Abstract: Constraints on neutron star masses and radii now come from a variety of sources: theoretical and experimental nuclear physics, astrophysical observations including pulsar timing, thermal and bursting X-ray sources, and gravitational waves, and the assumptions inherent to general relativity and causality of the equation of state. These measurements and assumptions also result in restrictions on the dense matter equation of state. The two most important structural parameters of neutron stars are their typical radii, which impacts intermediate densities in the range of one to two times the nuclear saturation density, and the maximum mass, which impacts the densities beyond about three times the saturation density. Especially intriguing has been the multi-messenger event GW170817, the first observed binary neutron star merger, which provided direct estimates of both stellar masses and radii as well as an upper bound to the maximum mass. Keywords: neutron stars; dense matter equation of state; nuclear structure; gravitational waves 1. Introduction The study of neutron stars represents our best chance to study matter under conditions of high density, extreme isospin asymmetry, and relatively cold temperatures which cannot be examined through heavy ion collisions. As explained below, neutron star matter is in strong- and weak-interaction −3 equilibrium, which for densities larger than the nuclear saturation density, ns ' 0.16 fm , which is the normal density found inside atomic nuclei, results in very neutron-rich compositions in which the neutron/proton ratio nn/np is 10 to 20. -

AST 248, Lecture 4
AST 248, Lecture 4 James Lattimer Department of Physics & Astronomy 449 ESS Bldg. Stony Brook University February 10, 2020 The Search for Intelligent Life in the Universe [email protected] James Lattimer AST 248, Lecture 4 Properties and Types of Stars Most stars are Main Sequence (M-S) stars, which burn H into He in their cores. Other groups are red giants, which have exhausted H fuel and \burn" He into C and O, supergiants which are burning even heavier elements, and white dwarfs (dead low-mass stars). M-S stars can be divided into spectral types O, B, A, F, G, K and M based on temperature or color. Note that there are diagonal lines www.daviddarling.info/encyclopedia/H/HRdiag.html of constant radius. James Lattimer AST 248, Lecture 4 Spectral Types Initial M-S M-S M-S M-S # in Spectral Mass Lum. Tsurface Life Radius Galaxy ◦ Type (M )L K (years) (R ) O 60 800,000 50,000 1 · 106 12 5:5 · 104 B 6 800 15,000 1 · 108 3.9 3:6 · 108 A 2 14 8000 2 · 109 1.7 2:4 · 109 F 1.3 3.2 6500 6 · 109 1.3 1:2 · 1010 G 0.9 0.8 5500 1:3 · 1010 0.92 2:8 · 1010 K 0.7 0.2 4000 4 · 1010 0.72 6 · 1010 M 0.2 0.01 3000 2:5 · 1011 0.3 3 · 1011 James Lattimer AST 248, Lecture 4 M-S Properties Related I A star's physical properties on the Main Sequence (M-S) 1=2 are related: Tcenter / M=R; R / M 2 4 I A star radiates like a blackbody, so L / R T I Approximately Tcenter / Tsurface = T . -

Astrophysical Transients: Multi-Messenger Probes of Nuclear Physics
INT 11-2b Astrophysical Transients: Multi-messenger Probes of Nuclear Physics Week 4: Microphysical inputs (equation of state, rates, opacities) to macroscopic models August 1 – 5, 2011 Monday, August 1, 2011 Room C421, Physics and Astronomy Tower • 10:30~ Andrew Steiner, INT "Determining the Equation of State of Dense Matter from Neutron Star Mass and Radius Determinations" Room A114, Physics and Astronomy Auditorium • 3:00 ~ Joe Carlson, LANL “Homogeneous and Inhomogenous Neutron Matter” • 3:30 ~ Kai Hebeler, Ohio State Univ “Chiral three-body forces and neutron-rich matter” • 4:00 ~ Hans-Josef Schulze, INFN Catania “The Maximum Mass Problem”- Tuesday, August 2, 2011 Room C421, Physics and Astronomy Tower • 10:30 ~ Ray Sawyer, UC Santa Barbara “Plasma Corrections to Rates: A More Serious Issue Than it May Seem” • 11:30 ~ Armen Sedrakian, J. W. Goethe Univ “Color Superconducting Compact Stars: Structure, Cooling and Gravitational Radiation” Room A114, Physics and Astronomy Auditorium • 3:00 ~ Madappa Prakash, Ohio University Discussion • 3:30 ~ Andrew Steiner, INT, and Christian Ott, Caltech Discussion Wednesday, August 3, 2011 Room C421, Physics and Astronomy Tower • 10:30 ~ Vincenzo Cirigliano, LANL "A Low-energy Effective Theory of the Neutron Star Crust” • 11:30 ~ Joseph Hughto, Indiana University "Structure and Shear Modulus of the Neutron Star Crust” Room A114, Physics and Astronomy Auditorium • 3:00 ~ André da Silva Schneider, Indiana Univ "Molecular Dynamics Simulations of the Neutron Star Crust: Freezing and Chemical Separation" -

Michael Zingale / Curriculum Vitæ
Michael Zingale / Curriculum Vitæ Department of Physics and Astronomy, Stony Brook University, Stony Brook, NY 11794-3800 e-mail: [email protected] phone: (631) 632-8225 web: https://zingale.github.io : zingale 7 : @Michael_Zingale u : michaelzingale ORCiD : 0000-0001-8401-030X Present Position Sept. 2021– Professor of Physics and Astronomy, Stony Brook University, Stony Brook, NY Research Interests I am interested in developing and applying computational hydrodynamics algorithms to problems in nuclear astrophysics. A large part of this work is the development of low Mach number hydrody- namics code MAESTROeX and the compressible (magneto-, radiation-) hydrodynamics code Castro. Both codes are freely available on github, use adaptive mesh refinement, and hybrid parallelism techniques to run at scale on today’s supercomputers. I apply these codes to studies of X-ray bursts, different progenitor models of Type Ia supernovae, and convection in stars. Importantly, all of the code, input files, workflow scripts needed to reproduce the science done in my research group is available in our github repos. Education 2000 Ph.D. in Astronomy and Astrophysics, University of Chicago thesis: Helium Detonations on Neutron Stars advisor: Dr. J. W. Truran 1998 M.S. in Astronomy and Astrophysics, University of Chicago 1996 B.S. in Physics and Astronomy, University of Rochester, Magna Cum Laude thesis: Magnetohydrodynamical Wave Support of Molecular Clouds Minor in Mathematics, University of Rochester Academic Appointments 2014– Affiliate, Institute for Advanced Computational Science, Stony Brook University 2012–2021 Associate Professor of Physics and Astronomy, Stony Brook University 2006–2011 Assistant Professor of Physics and Astronomy, Stony Brook University 2001–2005 Postdoctoral Researcher, SciDAC Supernova Science Center, University of California, Santa Cruz. -

Towards a Better Understanding of the Symmetry Energy Within Neutron Stars
Towards a better understanding of the symmetry energy within neutron stars C.Y. Tsang (曾浚源), M.B. Tsang (曾敏兒)#, P. Danielewicz, and W.G. Lynch (連致標) National Superconducting Cyclotron Laboratory and the Department of Physics and Astronomy Michigan State University, East Lansing, MI 48824 USA and F.J. Fattoyev Center for Exploration of Energy and Matter Department of Physics, Indiana University, Bloomington, IN 47408 USA Abstract The LIGO-Virgo collaboration’s ground-breaking detection of the binary neutron-star merger event, GW170817, has expanded efforts to understand the Equation of State (EoS) of nuclear matter. These measurements provide new constraints on the overall pressure, but do not, by itself, elucidate its microscopic origins, including the pressure arising from the symmetry energy, that governs much of the internal structure of a neutron star. To correlate microscopic constraints from nuclear measurements to the GW170817 constraints, we calculate neutron star properties with more than 200 Skyrme energy density functionals that describe properties of nuclei. Calcuated neutron-star radii (R) and the tidal deformabilities (Λ) show a strong correlation with pressure at twice saturation density. By combining the neutron star EoS extracted from the GW170817 event and the EoS of symmetric matter from nucleus-nucleus collision experiments, we extract the density dependence of the symmetry pressure from 1.2ρ0 to 4.5ρ0. While the uncertainties in the symmetry pressure are large, they can be reduced with new experimental and astrophysical results. Email addresses: #Corresponding Author: [email protected] C.Y. Tsang: [email protected] W.G. Lynch: [email protected] P. -

AST 301, Lecture 3
AST 301, Lecture 3 James Lattimer Department of Physics & Astronomy 449 ESS Bldg. Stony Brook University February 3, 2019 Cosmic Catastrophes (AKA Collisions) [email protected] James Lattimer AST 301, Lecture 3 Properties and Types of Stars Most stars are Main Sequence (M-S) stars, which burn H into He in their cores. Other groups are red giants, which have exhausted H fuel and \burn" He into C and O, supergiants which are burning even heavier elements, and white dwarfs (dead low-mass stars). M-S stars can be divided into spectral types O, B, A, F, G, K and M based on temperature or color. Note that there are diagonal lines www.daviddarling.info/encyclopedia/H/HRdiag.html of constant radius. James Lattimer AST 301, Lecture 3 Spectral Types Initial M-S M-S M-S M-S # in Spectral Mass Lum. Tsurface Life Radius Galaxy ◦ Type (M )L K (years) (R ) O 60 800,000 50,000 1 · 106 12 5:5 · 104 B 6 800 15,000 1 · 108 3.9 3:6 · 108 A 2 14 8000 2 · 109 1.7 2:4 · 109 F 1.3 3.2 6500 6 · 109 1.3 1:2 · 1010 G 0.9 0.8 5500 1:3 · 1010 0.92 2:8 · 1010 K 0.7 0.2 4000 4 · 1010 0.72 6 · 1010 M 0.2 0.01 3000 2:5 · 1011 0.3 3 · 1011 James Lattimer AST 301, Lecture 3 M-S Properties Related I A star's physical properties on the Main Sequence (M-S) 1=2 are related: Tcenter / M=R; R / M 2 4 I A star radiates like a blackbody, so L / R T I Approximately Tcenter / Tsurface = T . -

2Majors and Minors.Qxd.KA
Spring 2007: updates since Fall 2006 are in red PHYSICS Physics (PHY) Major and Minor in Physics Department of Physics and Astronomy, College of Arts and Sciences CHAIRPERSON: Peter Koch ASSISTANT TO THE CHAIR: Pam Burris DIRECTOR OF UNDERGRADUATE STUDIES: Deane Peterson ASSISTANT TO THE DIRECTOR: Elaine Larsen ASTRONOMY COORDINATOR: James Lattimer E-MAIL: [email protected] OFFICE: P-110 Physics PHONE: (631) 632-8036, 632-8100 WEB ADDRESS: http://www.physics.sunysb.edu Minors of particular interest to students majoring in Physics: Computer Science (CSE), Electrical Engineering (ESE), Materials Science (ESM), Mathematics (MAT), Science and Engineering (LSE) Faculty ture physics. California, San Diego: Experimental solid-state Alexander Abanov, Associate Professor, Ph.D., Paul D. Grannis, Distinguished Professor, physics. University of Chicago: Theoretical condensed Ph.D., University of California, Berkeley: Robert L. McCarthy, Professor, Ph.D., matter physics. Experimental high-energy physics; elementary University of California, Berkeley: Experimental Philip B. Allen, Professor, Ph.D., University of particle reactions. elementary particle physics. California, Berkeley: Theoretical solid-state Michael Gurvitch, Professor, Ph.D., Stony Barry M. McCoy, Distinguished Professor, physics; superconductors and superconductivity. Brook University: Experimental solid-state Ph.D., Harvard University: Statistical mechan- Meigan Aronson, Professor, Ph.D., University of physics. ics. Member, Yang Institute for Theoretical Illinois Urbana-Champaign: Experimental solid- Thomas Hemmick, Professor, Ph.D., University Physics. state physics. of Rochester: Experimental relativistic heavy-ion Robert L. McGrath, Professor, Provost and Vice Ralf Averbeck, Research Assistant Professor, nuclear physics. Recipient of the State President of Brookhaven Affairs; Ph.D., Ph.D., Universitaet Giessen, Germany: University Chancellor’s Award for Excellence in University of Iowa: Experimental physics; nuclear Experimental nuclear physics. -

Equation of State Constraints from Neutron Stars
Equation of State Constraints from Neutron Stars James Lattimer [email protected] Department of Physics & Astronomy Stony Brook University J.M. Lattimer, Isolated Neutron Stars, London, 27 April 2006 – p.1/?? Credit: Dany Page, UNAMJ.M. Lattimer, Isolated Neutron Stars, London, 27 April 2006 – p.2/?? Observable Quantities (1) • Mass • Limits softening from ‘exotica’ (hyperons, Bose condensates, quarks). 16 2 −3 • Limits highest possible density in stars: ρ< 1.4 × 10 (M⊙/M) g cm . • New evidence for Mmax > 1.5 M⊙. J.M. Lattimer, Isolated Neutron Stars, London, 27 April 2006 – p.3/?? Observed Masses J.M. Lattimer, Isolated Neutron Stars, London, 27 April 2006 – p.4/?? Observed Masses Black hole? ⇒ Firm lower mass limit?⇒ M > 1.6 M⊙, 95% confidence M > 1.68 M⊙ 95% confidence J.M. Lattimer, Isolated Neutron Stars, London, 27 April 2006 – p.5/?? Maximum Possible Density in Stars Causality limit for compactness: R ≥ 3GM/c2 (Lattimer, Masak, Prakash & Yahil 1990; Glendenning 1992) J.M. Lattimer, Isolated Neutron Stars, London, 27 April 2006 – p.6/?? Maximum Possible Density in Stars Causality limit for compactness: R ≥ 3GM/c2 (Lattimer, Masak, Prakash & Yahil 1990; Glendenning 1992) Uniform Density: 2 3 2 3M 3 c 1 15 M⊙ −3 ρc,UD = ≤ = 5.4 × 10 g cm 4πR3 4π 3G M 2 M But UD solution violates causality and ρsurface 6= 0. No realistic EOS has greater ρc for 2 given M than Tolman VII solution (ρ = ρc[1 − (r/R) ]) (Lattimer & Prakash 2005) 5 15 2 −3 Tolman VII : ρc,V II = ρc,Inc ≤ 13.6 × 10 (M⊙/M) g cm 2 J.M. -

Project Objectives, Work Progress and Achievements, Project Management
ENSAR 262010 – 3rd periodic report Project objectives, work progress and achievements, project management Project objectives for the period In order to carry out research at the forefront of fundamental nuclear science, our community of nuclear scientists profits from the diverse range of large research infrastructures existing in Europe. These infrastructures can supply different species of ion beams and energies but are complementary in their provision of beams and address different aspects of nuclear structure. In this way, we can learn how the nuclear forces arising from the interaction between the building blocks, i.e. neutrons and protons, manifest themselves in the rich structure of nuclei, and how different isotopes of elements are synthesised in primeval stellar processes. These European nuclear physics facilities are world-class and excel in comparison with facilities elsewhere in the world. Furthermore, the vibrant European nuclear physics community has made great efforts in the past to make the most efficient use of these facilities by developing the most advanced and novel equipment needed to pursue the excellent scientific programmes proposed at them. Our community also has a long tradition of applying state-of-the-art developments in nuclear instrumentation to other research fields (e.g. archaeology) and to benefit humanity (e.g. medical imaging). Together with multi-disciplinary and application-oriented research at these facilities, these activities ensure a high-level of socioeconomic impact. This work has been done under the auspices of NuPECC (Nuclear Physics European Collaboration Committee) and drawing support from previous EC framework programmes. Our community has delineated the steps needed to pursue coherent research programmes at these facilities. -
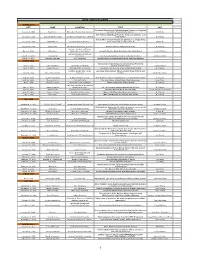
Inpp Spreadsheet
INPP SPREADSHEET WINTER 2008 DATE NAME LOCATION TITLE HOST Exclusive Reactions at High Momentum Transfer ( A Program January 8, 2008 Paul Stoler Rebssekaer Polytechnic Institute for Jlab for now and the future) Ken Hicks The Fermion Many-Body Problem: From Cold Atoms to Cold January 10, 2008 Michael McNeil Forbes University of Washington, Seattle Dark Matter M. Prakash Partial Wave Analysis Results for gamma p->p omega Using January 15, 2008 Mike Williams Carnegie Mellon University Data from CLAS at Jefferson Lab Ken Hicks January 18, 2008 Matt Braby Washington University St. Louis Particle Physics and Neutron Stars M. Prakash Institute for Nuclear Theory, March 4, 2008 Nir Barnea University of Washington Inelastic Electro-Weak Reactions with Light Nuclei Daniel Phillips Lawrence Livermore National March 11, 2008 John Becker Laboratory The Pure and Applied Science of Nuclear Isomers Andreas Schiller March 18, 2008 Matthias Schindler Ohio University An Introduction to Bayesian Methods and Data Analysis SPRING 2008 The Lick Observatory Supernova Search and Follow-Up April 2, 2008 Alex Fillippenko University of Berkeley Studies on Supernovae Joseph Shields April 8, 2008 Edward Brown Michigan State University Journey to the Core of an Accreting Neutron Star M. Prakash Goddard Space Flight Center, Accreting X-Ray Pulsars Observed with Integral,RXTE and April 15, 2008 Katja Pattschmidt Maryland Suzaku Markus Boettcher April 22, 2008 Andrew Cumming McGill University, Canada New Regimes of Nuclear Burning on Accreting Neutron Stars M. Prakash April 29, 2008 Thomas Statler Ohio University The Spin States of Small Near-Earth Asteroids Doug Clowe May 6, 2008 Duncan Lorimer University of West Virginia What's New in the Pulsar World? M.