Error-Correcting Codes
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![A [49 16 6 ]-Linear Code As Product of the [7 4 2 ] Code Due to Aunu and the Hamming [7 4 3 ] Code](https://docslib.b-cdn.net/cover/2633/a-49-16-6-linear-code-as-product-of-the-7-4-2-code-due-to-aunu-and-the-hamming-7-4-3-code-232633.webp)
A [49 16 6 ]-Linear Code As Product of the [7 4 2 ] Code Due to Aunu and the Hamming [7 4 3 ] Code
General Letters in Mathematics, Vol. 4, No.3 , June 2018, pp.114 -119 Available online at http:// www.refaad.com https://doi.org/10.31559/glm2018.4.3.4 A [49 16 6 ]-Linear Code as Product Of The [7 4 2 ] Code Due to Aunu and the Hamming [7 4 3 ] Code CHUN, Pamson Bentse1, IBRAHIM Alhaji Aminu2, and MAGAMI, Mohe'd Sani3 1 Department Of Mathematics, Plateau State University Bokkos, Jos Nigeria [email protected] 2 Department Of Mathematics, Usmanu Danfodiyo University Sokoto, Sokoto Nigeria [email protected] 3 Department Of Mathematics, Usmanu Danfodiyo University Sokoto, Sokoto Nigeria [email protected] Abstract: The enumeration of the construction due to "Audu and Aminu"(AUNU) Permutation patterns, of a [ 7 4 2 ]- linear code which is an extended code of the [ 6 4 1 ] code and is in one-one correspondence with the known [ 7 4 3 ] - Hamming code has been reported by the Authors. The [ 7 4 2 ] linear code, so constructed was combined with the known Hamming [ 7 4 3 ] code using the ( u|u+v)-construction method to obtain a new hybrid and more practical single [14 8 3 ] error- correcting code. In this paper, we provide an improvement by obtaining a much more practical and applicable double error correcting code whose extended version is a triple error correcting code, by combining the same codes as in [1]. Our goal is achieved through using the product code construction approach with the aid of some proven theorems. Keywords: Cayley tables, AUNU Scheme, Hamming codes, Generator matrix,Tensor product 2010 MSC No: 97H60, 94A05 and 94B05 1. -

Coding Theory: Linear Error-Correcting Codes Coding Theory Basic Definitions Error Detection and Correction Finite Fields Anna Dovzhik
Coding Theory: Linear Error- Correcting Codes Anna Dovzhik Outline Coding Theory: Linear Error-Correcting Codes Coding Theory Basic Definitions Error Detection and Correction Finite Fields Anna Dovzhik Linear Codes Hamming Codes Finite Fields Revisited BCH Codes April 23, 2014 Reed-Solomon Codes Conclusion Coding Theory: Linear Error- Correcting 1 Coding Theory Codes Basic Definitions Anna Dovzhik Error Detection and Correction Outline Coding Theory 2 Finite Fields Basic Definitions Error Detection and Correction 3 Finite Fields Linear Codes Linear Codes Hamming Codes Hamming Codes Finite Fields Finite Fields Revisited Revisited BCH Codes BCH Codes Reed-Solomon Codes Reed-Solomon Codes Conclusion 4 Conclusion Definition A q-ary word w = w1w2w3 ::: wn is a vector where wi 2 A. Definition A q-ary block code is a set C over an alphabet A, where each element, or codeword, is a q-ary word of length n. Basic Definitions Coding Theory: Linear Error- Correcting Codes Anna Dovzhik Definition If A = a ; a ;:::; a , then A is a code alphabet of size q. Outline 1 2 q Coding Theory Basic Definitions Error Detection and Correction Finite Fields Linear Codes Hamming Codes Finite Fields Revisited BCH Codes Reed-Solomon Codes Conclusion Definition A q-ary block code is a set C over an alphabet A, where each element, or codeword, is a q-ary word of length n. Basic Definitions Coding Theory: Linear Error- Correcting Codes Anna Dovzhik Definition If A = a ; a ;:::; a , then A is a code alphabet of size q. Outline 1 2 q Coding Theory Basic Definitions Error Detection Definition and Correction Finite Fields A q-ary word w = w1w2w3 ::: wn is a vector where wi 2 A. -

Mceliece Cryptosystem Based on Extended Golay Code
McEliece Cryptosystem Based On Extended Golay Code Amandeep Singh Bhatia∗ and Ajay Kumar Department of Computer Science, Thapar university, India E-mail: ∗[email protected] (Dated: November 16, 2018) With increasing advancements in technology, it is expected that the emergence of a quantum computer will potentially break many of the public-key cryptosystems currently in use. It will negotiate the confidentiality and integrity of communications. In this regard, we have privacy protectors (i.e. Post-Quantum Cryptography), which resists attacks by quantum computers, deals with cryptosystems that run on conventional computers and are secure against attacks by quantum computers. The practice of code-based cryptography is a trade-off between security and efficiency. In this chapter, we have explored The most successful McEliece cryptosystem, based on extended Golay code [24, 12, 8]. We have examined the implications of using an extended Golay code in place of usual Goppa code in McEliece cryptosystem. Further, we have implemented a McEliece cryptosystem based on extended Golay code using MATLAB. The extended Golay code has lots of practical applications. The main advantage of using extended Golay code is that it has codeword of length 24, a minimum Hamming distance of 8 allows us to detect 7-bit errors while correcting for 3 or fewer errors simultaneously and can be transmitted at high data rate. I. INTRODUCTION Over the last three decades, public key cryptosystems (Diffie-Hellman key exchange, the RSA cryptosystem, digital signature algorithm (DSA), and Elliptic curve cryptosystems) has become a crucial component of cyber security. In this regard, security depends on the difficulty of a definite number of theoretic problems (integer factorization or the discrete log problem). -

Final-Del-Lab-Manual-2018-19
LAB MANUAL DIGITAL ELECTRONICS LABORATORY Subject Code: 210246 2018 - 19 INDEX Batch : - Page Date of Date of Signature of Sr.No Title No Conduction Submission Staff GROUP - A Realize Full Adder and Subtractor using 1 a) Basic Gates and b) Universal Gates Design and implement Code converters-Binary to Gray and BCD to 2 Excess-3 Design of n-bit Carry Save Adder (CSA) and Carry Propagation Adder (CPA). Design and Realization of BCD 3 Adder using 4-bit Binary Adder (IC 7483). Realization of Boolean Expression for suitable combination logic using MUX 4 74151 / DMUX 74154 Verify the truth table of one bit and two bit comparators using logic gates and 5 comparator IC Design & Implement Parity Generator 6 using EX-OR. GROUP - B Flip Flop Conversion: Design and 7 Realization Design of Ripple Counter using suitable 8 Flip Flops a. Realization of 3 bit Up/Down Counter using MS JK Flip Flop / D-FF 9 b. Realization of Mod -N counter using ( 7490 and 74193 ) Design and Realization of Ring Counter 10 and Johnson Ring counter Design and implement Sequence 11 generator using JK flip-flop INDEX Batch : - Design and implement pseudo random 12 sequence generator. Design and implement Sequence 13 detector using JK flip-flop Design of ASM chart using MUX 14 controller Method. GROUP - C Design and Implementation of 15 Combinational Logic using PLAs. Design and simulation of - Full adder , 16 Flip flop, MUX using VHDL (Any 2) Use different modeling styles. Design & simulate asynchronous 3- bit 17 counter using VHDL. Design and Implementation of 18 Combinational Logic using PALs GROUP - D Study of Shift Registers ( SISO,SIPO, 19 PISO,PIPO ) Study of TTL Logic Family: Feature, 20 Characteristics and Comparison with CMOS Family Study of Microcontroller 8051 : 21 Features, Architecture and Programming Model ` Digital Electronics Lab (Pattern 2015) GROUP - A Digital Electronics Lab (Pattern 2015) Assignment: 1 Title: Adder and Subtractor Objective: 1. -

Coded Computing Via Binary Linear Codes: Designs and Performance Limits Mahdi Soleymani∗, Mohammad Vahid Jamali∗, and Hessam Mahdavifar, Member, IEEE
1 Coded Computing via Binary Linear Codes: Designs and Performance Limits Mahdi Soleymani∗, Mohammad Vahid Jamali∗, and Hessam Mahdavifar, Member, IEEE Abstract—We consider the problem of coded distributed processing capabilities. A coded computing scheme aims to computing where a large linear computational job, such as a divide the job to k < n tasks and then to introduce n − k matrix multiplication, is divided into k smaller tasks, encoded redundant tasks using an (n; k) code, in order to alleviate the using an (n; k) linear code, and performed over n distributed nodes. The goal is to reduce the average execution time of effect of slower nodes, also referred to as stragglers. In such a the computational job. We provide a connection between the setup, it is often assumed that each node is assigned one task problem of characterizing the average execution time of a coded and hence, the total number of encoded tasks is n equal to the distributed computing system and the problem of analyzing the number of nodes. error probability of codes of length n used over erasure channels. Recently, there has been extensive research activities to Accordingly, we present closed-form expressions for the execution time using binary random linear codes and the best execution leverage coding schemes in order to boost the performance time any linear-coded distributed computing system can achieve. of distributed computing systems [6]–[18]. However, most It is also shown that there exist good binary linear codes that not of the work in the literature focus on the application of only attain (asymptotically) the best performance that any linear maximum distance separable (MDS) codes. -

A New Approach to the Snake-In-The-Box Problem
462 ECAI 2012 Luc De Raedt et al. (Eds.) © 2012 The Author(s). This article is published online with Open Access by IOS Press and distributed under the terms of the Creative Commons Attribution Non-Commercial License. doi:10.3233/978-1-61499-098-7-462 A New Approach to the Snake-In-The-Box Problem David Kinny1 Abstract. The “Snake-In-The-Box” problem, first described more Research on the SIB problem initially focused on applications in than 50 years ago, is a hard combinatorial search problem whose coding [14]. Coils are spread-k circuit codes for k =2, in which solutions have many practical applications. Until recently, techniques n-words k or more positions apart in the code differ in at least k based on Evolutionary Computation have been considered the state- bit positions [12]. (The well-known Gray codes are spread-1 circuit of-the-art for solving this deterministic maximization problem, and codes.) Longest snakes and coils provide the maximum number of held most significant records. This paper reviews the problem and code words for a given word size (i.e., hypercube dimension). prior solution techniques, then presents a new technique, based on A related application is in encoding schemes for analogue-to- Monte-Carlo Tree Search, which finds significantly better solutions digital converters including shaft (rotation) encoders. Longest SIB than prior techniques, is considerably faster, and requires no tuning. codes provide greatest resolution, and single bit errors are either recognised as such or map to an adjacent codeword causing an off- 1 INTRODUCTION by-one error. -

ERROR CORRECTING CODES Definition (Alphabet)
ERROR CORRECTING CODES Definition (Alphabet) An alphabet is a finite set of symbols. Example: A simple example of an alphabet is the set A := fB; #; 17; P; $; 0; ug. Definition (Codeword) A codeword is a string of symbols in an alphabet. Example: In the alphabet A := fB; #; 17; P; $; 0; ug, some examples of codewords of length 4 are: P 17#u; 0B$#; uBuB; 0000: Definition (Code) A code is a set of codewords in an alphabet. Example: In the alphabet A := fB; #; 17; P; $; 0; ug, an example of a code is the set of 5 words: fP 17#u; 0B$#; uBuB; 0000;PP #$g: If all the codewords are known and recorded in some dictionary then it is possible to transmit messages (strings of codewords) to another entity over a noisy channel and detect and possibly correct errors. For example in the code C := fP 17#u; 0B$#; uBuB; 0000;PP #$g if the word 0B$# is sent and received as PB$#, then if we knew that only one error was made it can be determined that the letter P was an error which can be corrected by changing P to 0. Definition (Linear Code) A linear code is a code where the codewords form a finite abelian group under addition. Main Problem of Coding Theory: To construct an alphabet and a code in that alphabet so it is as easy as possible to detect and correct errors in transmissions of codewords. A key idea for solving this problem is the notion of Hamming distance. Definition (Hamming distance dH ) Let C be a code and let 0 0 0 0 w = w1w2 : : : wn; w = w1w2 : : : wn; 0 0 be two codewords in C where wi; wj are elements of the alphabet of C. -

NOTE on GRAY CODES for PERMUTATION LISTS Seymour
PUBLICATIONS DE L’INSTITUT MATHEMATIQUE´ Nouvelle s´erie,tome 78(92) (2005), 87–92 NOTE ON GRAY CODES FOR PERMUTATION LISTS Seymour Lipschutz, Jie Gao, and Dianjun Wang Communicated by Slobodan Simi´c Abstract. Robert Sedgewick [5] lists various Gray codes for the permutations in Sn including the classical algorithm by Johnson and Trotter. Here we give an algorithm which constructs many families of Gray codes for Sn, which closely follows the construction of the Binary Reflexive Gray Code for the n-cube Qn. 1. Introduction There are (n!)! ways to list the n! permutations in Sn. Some such permutation lists have been generated by a computer, and some such permutation lists are Gray codes (where successive permutations differ by a transposition). One such famous Gray code for Sn is by Johnson [4] and Trotter [6]. In fact, each new permutation in the Johnson–Trotter (JT ) list for Sn is obtained from the preceding permutation by an adjacent transposition. Sedgewick [5] gave a survey of various Gray codes for Sn in 1977. Subsequently, Conway, Sloane and Wilks [1] gave a new Gray code CSW for Sn in 1989 while proving the existence of Gray codes for the reflection groups. Recently, Gao and Wang [2] gave simple algorithms, each with an efficient implementation, for two new permutation lists GW1 and GW2 for Sn, where the second such list is a Gray code for Sn. The four lists, JT , CSW , GW1 and GW2, for n = 4, are pictured in Figure 1. This paper gives an algorithm for constructing many families of Gray codes for Sn which uses an idea from the construction of the Binary Reflected Gray Code (BRGC) of the n-cube Qn. -

Other Binary Codes (3A)
Other Binary Codes (3A) Young Won Lim 1/3/14 Copyright (c) 2011-2013 Young W. Lim. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled "GNU Free Documentation License". Please send corrections (or suggestions) to [email protected]. This document was produced by using OpenOffice and Octave. Young Won Lim 1/3/14 Coding A code is a rule for converting a piece of information (for example, a letter, word, phrase, or gesture) into another form or representation (one sign into another sign), not necessarily of the same type. In communications and information processing, encoding is the process by which information from a source is converted into symbols to be communicated. Decoding is the reverse process, converting these code symbols back into information understandable by a receiver. Young Won Lim Other Binary Codes (4A) 3 1/3/14 Character Coding ASCII code BCD (Binary Coded Decimal) definitions for 128 characters: Number characters (0-9) 33 non-printing control characters (many now obsolete) 95 printable charactersi Young Won Lim Other Binary Codes (4A) 4 1/3/14 Representation of Numbers Fixed Point Number representation ● 2's complement +1234 ● 1's complement 0 -582978 coding ● sign-magnitude Floating Point Number representation +23.84380 ● IEEE 754 -1.388E+08 -

Loopless Gray Code Enumeration and the Tower of Bucharest
Loopless Gray Code Enumeration and the Tower of Bucharest Felix Herter1 and Günter Rote1 1 Institut für Informatik, Freie Universität Berlin Takustr. 9, 14195 Berlin, Germany [email protected], [email protected] Abstract We give new algorithms for generating all n-tuples over an alphabet of m letters, changing only one letter at a time (Gray codes). These algorithms are based on the connection with variations of the Towers of Hanoi game. Our algorithms are loopless, in the sense that the next change can be determined in a constant number of steps, and they can be implemented in hardware. We also give another family of loopless algorithms that is based on the idea of working ahead and saving the work in a buffer. 1998 ACM Subject Classification F.2.2 Nonnumerical Algorithms and Problems Keywords and phrases Tower of Hanoi, Gray code, enumeration, loopless generation Contents 1 Introduction: the binary reflected Gray code and the Towers of Hanoi 2 1.1 The Gray code . .2 1.2 Loopless algorithms . .2 1.3 The Tower of Hanoi . .3 1.4 Connections between the Towers of Hanoi and Gray codes . .4 1.5 Loopless Tower of Hanoi and binary Gray code . .4 1.6 Overview . .4 2 Ternary Gray codes and the Towers of Bucharest 5 3 Gray codes with general radixes 7 4 Generating the m-ary Gray code with odd m 7 5 Generating the m-ary Gray code with even m 9 arXiv:1604.06707v1 [cs.DM] 22 Apr 2016 6 The Towers of Bucharest++ 9 7 Simulation 11 8 Working ahead 11 8.1 An alternative STEP procedure . -
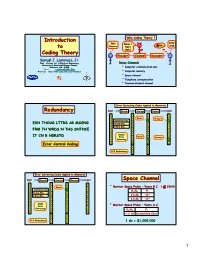
Introduction to Coding Theory
Introduction Why Coding Theory ? Introduction Info Info Noise ! Info »?# Sink to Source Heh ! Sink Heh ! Coding Theory Encoder Channel Decoder Samuel J. Lomonaco, Jr. Dept. of Comp. Sci. & Electrical Engineering Noisy Channels University of Maryland Baltimore County Baltimore, MD 21250 • Computer communication line Email: [email protected] WebPage: http://www.csee.umbc.edu/~lomonaco • Computer memory • Space channel • Telephone communication • Teacher/student channel Error Detecting Codes Applied to Memories Redundancy Input Encode Storage Detect Output 1 1 1 1 0 0 0 0 1 1 Error 1 Erasure 1 1 31=16+5 Code 1 0 ? 0 0 0 0 EVN THOUG LTTRS AR MSSNG 1 16 Info Bits 1 1 1 0 5 Red. Bits 0 0 0 0 0 0 0 FRM TH WRDS N THS SNTNCE 1 1 1 1 0 0 0 0 1 1 1 Double 1 IT CN B NDRSTD 0 0 0 0 1 Error 1 Error 1 Erasure 1 1 Detecting 1 0 ? 0 0 0 0 1 1 1 1 Error Control Coding 0 0 1 1 0 0 31% Redundancy 1 1 1 1 Error Correcting Codes Applied to Memories Input Encode Storage Correct Output Space Channel 1 1 1 1 0 0 0 0 Mariner Space Probe – Years B.C. ( ≤ 1964) 1 1 Error 1 1 • 1 31=16+5 Code 1 0 1 0 0 0 0 Eb/N0 Pe 16 Info Bits 1 1 1 1 -3 0 5 Red. Bits 0 0 0 6.8 db 10 0 0 0 0 -5 1 1 1 1 9.8 db 10 0 0 0 0 1 1 1 Single 1 0 0 0 0 Error 1 1 • Mariner Space Probe – Years A.C. -

Algorithms for Generating Binary Reflected Gray Code Sequence: Time Efficient Approaches
2009 International Conference on Future Computer and Communication Algorithms for Generating Binary Reflected Gray Code Sequence: Time Efficient Approaches Md. Mohsin Ali, Muhammad Nazrul Islam, and A. B. M. Foysal Dept. of Computer Science and Engineering Khulna University of Engineering & Technology Khulna – 9203, Bangladesh e-mail: [email protected], [email protected], and [email protected] Abstract—In this paper, we propose two algorithms for Coxeter groups [4], capanology (the study of bell-ringing) generating a complete n-bit binary reflected Gray code [5], continuous space-filling curves [6], classification of sequence. The first one is called Backtracking. It generates a Venn diagrams [7]. Today, Gray codes are widely used to complete n-bit binary reflected Gray code sequence by facilitate error correction in digital communications such as generating only a sub-tree instead of the complete tree. In this digital terrestrial television and some cable TV systems. approach, both the sequence and its reflection for n-bit is In this paper, we present the derivation and generated by concatenating a “0” and a “1” to the most implementation of two algorithms for generating the significant bit position of the n-1 bit result generated at each complete binary reflected Gray code sequence leaf node of the sub-tree. The second one is called MOptimal. It () ≤ ≤ n − is the modification of a Space and time optimal approach [8] G i ,0 i 2 1 , for a given number of bits n. We by considering the minimization of the total number of outer evaluate the performance of these algorithms and other and inner loop execution for this purpose.