DOCSLIB.ORG

A Sharp Divergence Theorem with Nontangential Traces

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Sharp Divergence Theorem with Nontangential Traces A Sharp Divergence Theorem with Nontangential Traces Dorina Mitrea, Irina Mitrea, and Marius Mitrea 1. A Brief Historical Perspective functions on a compact interval [푎, 푏], the Fundamental The Fundamental Theorem of Calculus, one of the most Theorem of Calculus reads: spectacular scientific achievements, stands as beautiful, 푏 powerful, and relevant today as it did more than three ∫ 퐹′(푥) 푑푥 = 퐹(푏) − 퐹(푎) (1.1) centuries ago when it first emerged onto the mathemati- 푎 cal scene. Typically, Isaac Newton and Gottfried Leibniz for every 퐹 ∈ AC([푎, 푏]). are credited with developing much of the mathematical It is a stark example of how local information, encoded in machinery associated with this result into a coherent the- the instantaneous rate of change (aka derivative) 퐹′, can ory for infinitesimal quantities (the bedrock of modern cal- be pieced together via integration to derive conclusions of culus), a mathematical landscape within which the Fun- a global nature about the variation of 퐹 over [푎, 푏], a fun- damental Theorem of Calculus stands out as the crown- damental paradigm in calculus. ing achievement. In its sharp one-dimensional version, Intriguingly, while (1.1) is essentially optimal, dealing involving the class AC([푎, 푏]) of absolutely continuous with higher-dimensional versions of the Fundamental The- Dorina Mitrea is a professor of mathematics at Baylor University. Her email orem of Calculus remains an active area of research in con- 푛 address is [email protected]. temporary mathematics. In its standard version, with ℒ Irina Mitrea is a professor of mathematics at Temple University. Her email denoting the 푛-dimensional Lebesgue measure in ℝ푛, the address is [email protected]. Divergence Theorem asserts that Marius Mitrea is a professor of mathematics at Baylor University. His email 푛 1 address is [email protected]. if Ω ⊆ ℝ is a bounded domain of class 풞 , Communicated by Notices Associate Editor Daniela De Silva. with outward unit normal 휈 and surface mea- ⃗ 푛 ⃗| (1.2) For permission to reprint this article, please contact: sure 휎, then ∫Ω div 퐹 푑ℒ = ∫휕Ω 휈 ⋅ (퐹|휕Ω) 푑휎 푛 [email protected]. for each vector field 퐹⃗ ∈ [풞1(Ω)] . DOI: https://doi.org/10.1090/noti2149 OCTOBER 2020 NOTICES OF THE AMERICAN MATHEMATICAL SOCIETY 1295 ′ 푛 Since the divergence of a continuously differentiable vec- where ퟏΩ is the characteristic function of Ω and 풟 (ℝ ) de- tor field 퐹⃗ may be computed pointwise as (div 퐹)(푥)⃗ = notes the space of distributions in ℝ푛. Conversely, since 푦−푥 푛 푛 −1 ⃗ 푛−1 both ∇ퟏΩ and −휈휎 are vector distributions in ℝ of order lim ℒ (퐵(푥, 푟)) ∫휕퐵(푥,푟) ( ) ⋅ 퐹(푦) 푑ℋ (푦), where 푟→0+ 푟 ≤ 1, their actions canonically extend to vector fields from ℋ 푛−1 stands for the (푛 − 1)-dimensional Hausdorff mea- 푛 [풞1(ℝ푛)] , in which scenario we recover (1.2). Hence, ℝ푛 (div 퐹)(푥)⃗ 푐 sure in , it follows that the quantity is em- (1.3) amounts to an equivalent reformulation of the classi- ⃗ blematic of the tendency of a vector field 퐹 to collect (sink cal Divergence Theorem (1.2), which has a purely geomet- effect) or disperse (source effect) at a point 푥. In view of ric measure theoretic nature. In particular, (1.3) brings this feature, the Divergence Formula in (1.2) may be re- into focus the fact that the distributional gradient of the garded as a conservation law, asserting that the solid inte- characteristic function of a bounded 풞1 domain is a locally gral of all such sources and sinks associated with a given finite Borel vector-valued measure in ℝ푛. vector field is equal to the net flow of said vector field As far as the latter property is concerned, R. Caccioppoli, 1 through the solid’s boundary. Hence, in complete anal- E. De Giorgi, and H. Federer registered a decisive leap for- ogy to the Fundamental Theorem of Calculus mentioned ward by considering the largest class of Euclidean subsets earlier, the Divergence Theorem describes how the infini- enjoying said property, i.e., the class of sets of locally fi- tesimal sink/source effects created by a vector field may be nite perimeter. It turns out that this consists of Lebesgue pieced together inside a given domain to produce a global, 푛 measurable subsets Ω of ℝ with the property that ퟏΩ is macroscopic effect along the boundary. 푛 푛 of locally bounded variation in ℝ , i.e., ퟏΩ ∈ BVloc(ℝ ). The classical result recorded in (1.2) is usually associ- 푛 In turn, membership to BVloc(ℝ ) is conceived in such a ated with the names of J.-L. Lagrange, who first established way that the Riesz Representation Theorem can naturally a special case of the Divergence Theorem in 1762 working be applied to the functional on the propagation of sound waves (cf. [14]); C. F. Gauss, who independently considered a particular case in 1813 푛 1 푛 푛 Λ(퐹)⃗ ∶= ∫ div 퐹⃗ 푑ℒ for all 퐹⃗ ∈ [풞푐 (ℝ )] , (1.4) (cf. [9]); M. V. Ostrogradsky, who gave the first proof of the Ω general theorem in 1826 (cf. [20]); G. Green, who used a to conclude that there exist a Borel measure 휎 in ℝ푛, related formula in 1828 (cf. [10]); A. Cauchy, who in 1846 ∗ which is actually supported on 휕Ω, and a 휎 -measurable first published, without proof, the nowadays familiar form ∗ vector-valued function 휈 ∶ ℝ푛 → ℝ푛 satisfying |휈| = 1 at of Green’s theorem (cf. [1]); B. Riemann, who provided a 휎 -a.e. point in ℝ푛, such that proof of Green’s formula in his 1851 inaugural disserta- ∗ tion (see [21]); Lord Kelvin, who in 1850 discovered a spe- 1 푛 푛 Λ(퐹)⃗ = ∫ 휈 ⋅ 퐹⃗ 푑휎∗ for all 퐹⃗ ∈ [풞푐 (ℝ )] . (1.5) cial version of Stokes’ theorem (in the three-dimensional ℝ푛 setting, also known as the curl theorem); and E.´ Cartan, 휈 who first published the general form of Stokes’ theorem (in The function is referred to as the geometric measure the- Ω 휎 the language of differential forms on manifolds) in 1945, oretic outward unit normal to . Bearing in mind that ∗ 휕Ω among others. However, a precise attribution is fraught is actually supported on , the following version of the with difficulty since the Divergence Theorem in its mod- Divergence Theorem emerges from (1.4) and (1.5): ern format has undergone successive waves of reformula- ⃗ 푛 ⃗ tions and generalizations, as well as more rigorous proofs, ∫ div 퐹 푑ℒ = ∫ 휈 ⋅ 퐹 푑휎∗ Ω 휕Ω (1.6) with inputs from a multitude of sources (general historical 푛 for each vector field 퐹⃗ ∈ [풞1(ℝ푛)] . accounts may be found in [12] and [22]). 푐 Specializing the Divergence Formula in (1.2) to the The real achievement of De Giorgi and Federer is further case when 퐹⃗ is the restriction to Ω of vector fields from refining (1.6) by establishing that actually 푛 [풞 ∞(ℝ푛)] (where 풞 ∞(ℝ푛) denotes the space of smooth, 푐 푐 휎 = ℋ 푛−1⌊휕 Ω, compactly supported functions in ℝ푛) yields the state- ∗ ∗ (1.7) ment: where 휕∗Ω denotes the measure theoretic boundary of Ω, if Ω ⊆ ℝ푛 is a bounded domain of class 풞1, defined as with outward unit normal 휈 and surface mea- (1.3) ℒ푛(퐵(푥, 푟) ∩ Ω) 푛 푛 ′ 푛 휕∗Ω ∶= {푥 ∈ ℝ ∶ lim sup 푛 > 0 and sure 휎, then ∇ퟏΩ = −휈휎 in [풟 (ℝ )] , 푟→0+ 푟 ℒ푛(퐵(푥, 푟) ⧵ Ω) lim sup 푛 > 0}. 푟→0+ 푟 1For instance, imagining 퐹⃗ as the velocity field of an incompressible fluid flow occupying a fixed region Ω, this informally states that “what goes in must come Hence, near points in 휕∗Ω there is enough mass (relative to out.” the scale) both in Ω and in ℝ푛 ⧵Ω. Let us also note that, in 1296 NOTICES OF THE AMERICAN MATHEMATICAL SOCIETY VOLUME 67, NUMBER 9 principle, 휕∗Ω can be a much smaller set than the topolog- Lipschitz domains, and also for a class of Reifenberg-flat ical boundary 휕Ω. Substituting (1.7) back into (1.6) then domains (cf. [3], [13]), but to go beyond this one needs yields the following result: genuinely new techniques. Progress in this regard has been registered in [11], which treats a much larger class of do- Theorem 1.1 (De Giorgi–Federer’s Divergence Theorem [4, mains than Lipschitz, without any flatness assumptions. 5,7,8]). Let Ω ⊆ ℝ푛 be a set of locally finite perimeter. Let 휈 be However, the version of the Divergence Theorem estab- the geometric measure theoretic outward unit normal to Ω, and 푛 lished in [11] requires that the (nontangential) trace of the let 휎 ∶= ℋ 푛−1⌊휕Ω. Then for each vector field 퐹⃗ ∈ [풞1(ℝ푛)] 푐 vector field 퐹⃗ on the boundary is 푝th power integrable for one has some 푝 > 1. This requirement is an artifact of the proof, ∫ (div 퐹⃗)| 푑ℒ푛 = ∫ 휈 ⋅ (퐹⃗| ) 푑휎. (1.8) which relies on the boundedness of the Hardy–Littlewood Ω 휕∗Ω 푝 Ω 휕∗Ω maximal function on 퐿 with 푝 > 1. The goal of this article is to describe a new brand of In a nutshell, one of the key results of the De Giorgi– Divergence Theorem developed in [17] exhibiting the fol- Federer theory is the identity lowing features (all of which are absent from De Giorgi– 푛−1 ∇ ퟏΩ = −휈 ℋ ⌊휕∗Ω Federer’s version of the Divergence Theorem recorded in as distributions in ℝ푛, whenever Theorem 1.1): • when 푛 = 1 and Ω is a finite interval on the real line, Ω ⊆ ℝ푛 , is a set of locally finite perimeter our theorem reduces precisely to the sharp version of the which may then readily be reinterpreted as the Divergence Fundamental Theorem of Calculus formulated in (1.1); Formula (1.8) simply by untangling jargon.
Load more

Recommended publications
  • A Brief Tour of Vector Calculus
    A BRIEF TOUR OF VECTOR CALCULUS A. HAVENS Contents 0 Prelude ii 1 Directional Derivatives, the Gradient and the Del Operator 1 1.1 Conceptual Review: Directional Derivatives and the Gradient........... 1 1.2 The Gradient as a Vector Field............................ 5 1.3 The Gradient Flow and Critical Points ....................... 10 1.4 The Del Operator and the Gradient in Other Coordinates*............ 17 1.5 Problems........................................ 21 2 Vector Fields in Low Dimensions 26 2 3 2.1 General Vector Fields in Domains of R and R . 26 2.2 Flows and Integral Curves .............................. 31 2.3 Conservative Vector Fields and Potentials...................... 32 2.4 Vector Fields from Frames*.............................. 37 2.5 Divergence, Curl, Jacobians, and the Laplacian................... 41 2.6 Parametrized Surfaces and Coordinate Vector Fields*............... 48 2.7 Tangent Vectors, Normal Vectors, and Orientations*................ 52 2.8 Problems........................................ 58 3 Line Integrals 66 3.1 Defining Scalar Line Integrals............................. 66 3.2 Line Integrals in Vector Fields ............................ 75 3.3 Work in a Force Field................................. 78 3.4 The Fundamental Theorem of Line Integrals .................... 79 3.5 Motion in Conservative Force Fields Conserves Energy .............. 81 3.6 Path Independence and Corollaries of the Fundamental Theorem......... 82 3.7 Green's Theorem.................................... 84 3.8 Problems........................................ 89 4 Surface Integrals, Flux, and Fundamental Theorems 93 4.1 Surface Integrals of Scalar Fields........................... 93 4.2 Flux........................................... 96 4.3 The Gradient, Divergence, and Curl Operators Via Limits* . 103 4.4 The Stokes-Kelvin Theorem..............................108 4.5 The Divergence Theorem ...............................112 4.6 Problems........................................114 List of Figures 117 i 11/14/19 Multivariate Calculus: Vector Calculus Havens 0.
    [Show full text]
  • Curl, Divergence and Laplacian
    Curl, Divergence and Laplacian What to know: 1. The definition of curl and it two properties, that is, theorem 1, and be able to predict qualitatively how the curl of a vector field behaves from a picture. 2. The definition of divergence and it two properties, that is, if div F~ 6= 0 then F~ can't be written as the curl of another field, and be able to tell a vector field of clearly nonzero,positive or negative divergence from the picture. 3. Know the definition of the Laplace operator 4. Know what kind of objects those operator take as input and what they give as output. The curl operator Let's look at two plots of vector fields: Figure 1: The vector field Figure 2: The vector field h−y; x; 0i: h1; 1; 0i We can observe that the second one looks like it is rotating around the z axis. We'd like to be able to predict this kind of behavior without having to look at a picture. We also promised to find a criterion that checks whether a vector field is conservative in R3. Both of those goals are accomplished using a tool called the curl operator, even though neither of those two properties is exactly obvious from the definition we'll give. Definition 1. Let F~ = hP; Q; Ri be a vector field in R3, where P , Q and R are continuously differentiable. We define the curl operator: @R @Q @P @R @Q @P curl F~ = − ~i + − ~j + − ~k: (1) @y @z @z @x @x @y Remarks: 1.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • The Divergence of a Vector Field.Doc 1/8
    9/16/2005 The Divergence of a Vector Field.doc 1/8 The Divergence of a Vector Field The mathematical definition of divergence is: w∫∫ A(r )⋅ds ∇⋅A()rlim = S ∆→v 0 ∆v where the surface S is a closed surface that completely surrounds a very small volume ∆v at point r , and where ds points outward from the closed surface. From the definition of surface integral, we see that divergence basically indicates the amount of vector field A ()r that is converging to, or diverging from, a given point. For example, consider these vector fields in the region of a specific point: ∆ v ∆v ∇⋅A ()r0 < ∇ ⋅>A (r0) Jim Stiles The Univ. of Kansas Dept. of EECS 9/16/2005 The Divergence of a Vector Field.doc 2/8 The field on the left is converging to a point, and therefore the divergence of the vector field at that point is negative. Conversely, the vector field on the right is diverging from a point. As a result, the divergence of the vector field at that point is greater than zero. Consider some other vector fields in the region of a specific point: ∇⋅A ()r0 = ∇ ⋅=A (r0) For each of these vector fields, the surface integral is zero. Over some portions of the surface, the normal component is positive, whereas on other portions, the normal component is negative. However, integration over the entire surface is equal to zero—the divergence of the vector field at this point is zero. * Generally, the divergence of a vector field results in a scalar field (divergence) that is positive in some regions in space, negative other regions, and zero elsewhere.
    [Show full text]
  • Part IA — Vector Calculus
    Part IA | Vector Calculus Based on lectures by B. Allanach Notes taken by Dexter Chua Lent 2015 These notes are not endorsed by the lecturers, and I have modified them (often significantly) after lectures. They are nowhere near accurate representations of what was actually lectured, and in particular, all errors are almost surely mine. 3 Curves in R 3 Parameterised curves and arc length, tangents and normals to curves in R , the radius of curvature. [1] 2 3 Integration in R and R Line integrals. Surface and volume integrals: definitions, examples using Cartesian, cylindrical and spherical coordinates; change of variables. [4] Vector operators Directional derivatives. The gradient of a real-valued function: definition; interpretation as normal to level surfaces; examples including the use of cylindrical, spherical *and general orthogonal curvilinear* coordinates. Divergence, curl and r2 in Cartesian coordinates, examples; formulae for these oper- ators (statement only) in cylindrical, spherical *and general orthogonal curvilinear* coordinates. Solenoidal fields, irrotational fields and conservative fields; scalar potentials. Vector derivative identities. [5] Integration theorems Divergence theorem, Green's theorem, Stokes's theorem, Green's second theorem: statements; informal proofs; examples; application to fluid dynamics, and to electro- magnetism including statement of Maxwell's equations. [5] Laplace's equation 2 3 Laplace's equation in R and R : uniqueness theorem and maximum principle. Solution of Poisson's equation by Gauss's method (for spherical and cylindrical symmetry) and as an integral. [4] 3 Cartesian tensors in R Tensor transformation laws, addition, multiplication, contraction, with emphasis on tensors of second rank. Isotropic second and third rank tensors.
    [Show full text]
  • Generalized Stokes' Theorem
    Chapter 4 Generalized Stokes’ Theorem “It is very difficult for us, placed as we have been from earliest childhood in a condition of training, to say what would have been our feelings had such training never taken place.” Sir George Stokes, 1st Baronet 4.1. Manifolds with Boundary We have seen in the Chapter 3 that Green’s, Stokes’ and Divergence Theorem in Multivariable Calculus can be unified together using the language of differential forms. In this chapter, we will generalize Stokes’ Theorem to higher dimensional and abstract manifolds. These classic theorems and their generalizations concern about an integral over a manifold with an integral over its boundary. In this section, we will first rigorously define the notion of a boundary for abstract manifolds. Heuristically, an interior point of a manifold locally looks like a ball in Euclidean space, whereas a boundary point locally looks like an upper-half space. n 4.1.1. Smooth Functions on Upper-Half Spaces. From now on, we denote R+ := n n f(u1, ... , un) 2 R : un ≥ 0g which is the upper-half space of R . Under the subspace n n n topology, we say a subset V ⊂ R+ is open in R+ if there exists a set Ve ⊂ R open in n n n R such that V = Ve \ R+. It is intuitively clear that if V ⊂ R+ is disjoint from the n n n subspace fun = 0g of R , then V is open in R+ if and only if V is open in R . n n Now consider a set V ⊂ R+ which is open in R+ and that V \ fun = 0g 6= Æ.
    [Show full text]
  • Metrics Defined by Bregman Divergences †
    1 METRICS DEFINED BY BREGMAN DIVERGENCES y PENGWEN CHEN z AND YUNMEI CHEN, MURALI RAOx Abstract. Bregman divergences are generalizations of the well known Kullback Leibler diver- gence. They are based on convex functions and have recently received great attention. We present a class of \squared root metrics" based on Bregman divergences. They can be regarded as natural generalization of Euclidean distance. We provide necessary and sufficient conditions for a convex function so that the square root of its associated average Bregman divergence is a metric. Key words. Metrics, Bregman divergence, Convexity subject classifications. Analysis of noise-corrupted data, is difficult without interpreting the data to have been randomly drawn from some unknown distribution with unknown parameters. The most common assumption on noise is Gaussian distribution. However, it may be inappropriate if data is binary-valued or integer-valued or nonnegative. Gaussian is a member of the exponential family. Other members of this family for example the Poisson and the Bernoulli are better suited for integer and binary data. Exponential families and Bregman divergences ( Definition 1.1 ) have a very intimate relationship. There exists a unique Bregman divergence corresponding to every regular exponential family [13][3]. More precisely, the log-likelihood of an exponential family distribution can be represented by a sum of a Bregman divergence and a parameter unrelated term. Hence, Bregman divergence provides a likelihood distance for exponential family in some sense. This property has been used in generalizing principal component analysis to the Exponential family [7]. The Bregman divergence however is not a metric, because it is not symmetric, and does not satisfy the triangle inequality.
    [Show full text]
  • LECTURE 27: the LAPLAST ONE Monday, November 25, 2019 5:23 PM
    LECTURE 27: THE LAPLAST ONE Monday, November 25, 2019 5:23 PM Today: Three little remaining topics related to Laplace I- 3 DIMENSIONS Previously: Solved Laplace's equation in 2 dimensions by converting it into polar coordinates. The same idea works in 3 dimensions if you use spherical coordinates. 3 Suppose u = u(x,y,z) solves u xx + u yy + u zz = 0 in R Using spherical coordinates, you eventually get urr + 2 ur + JUNK = 0 r (where r = x 2 + y 2 + z 2 and JUNK doesn't depend on r) If we're looking for radial solutions, we set JUNK = 0 Get u rr + 2 u r = 0 which you can solve to get r u(x,y,z) = -C + C' solves u xx + u yy + u zz = 0 r Finally, setting C = -1/(4π) and C' = 0, you get Fundamental solution of Laplace for n = 3 S(x,y,z) = 1 = 4πr 4π x 2 + y 2 + z 2 Note: In n dimensions, get u rr + n-1 ur = 0 r => u( r ) = -C + C' rn-2 => S(x) = Blah (for some complicated Blah) rn-1 Why fundamental? Because can build up other solutions from this! Fun Fact: A solution of -Δ u = f (Poisson's equation) in R n is u(x) = S(x) * f(x) = S(x -y) f(y) dy (Basically the constant is chosen such that -ΔS = d0 <- Dirac at 0) II - DERIVATION OF LAPLACE Two goals: Derive Laplace's equation, and also highlight an important structure of Δu = 0 A) SETTING n Definition: If F = (F 1, …, F n) is a vector field in R , then div(F) = (F 1)x1 + … + (F n)xn Notice : If u = u(x 1, …, x n), then u = (u x1 , …, u xn ) => div( u) = (u x1 )x1 + … + (u xn )xn = u x1 x1 + … + u xn xn = Δu Fact: Δu = div( u) "divergence structure" In particular, Laplace's equation works very well with the divergence theorem Divergence Theorem: F n dS = div(F) dx bdy D D B) DERIVATION Suppose you have a fluid F that is in equilibrium (think F = temperature or chemical concentration) Equilibrium means that for any region D, the net flux of F is 0.
    [Show full text]
  • Green Gauss Theorem Yesterday, We Continued Discussions on Index Notations That Can Be Used to Represent Tensors
    15/02/2017 LECTURE – 15 Green Gauss Theorem Yesterday, we continued discussions on index notations that can be used to represent tensors. In index notations we saw the Gradient of a scalar Divergence of a vector Cross product of vector etc. We also saw that a second rank tensor can be written as a sum of a symmetric & asymmetric tensor. 11 i.e, BBBBB[][] ij22 ij ji ij ji First part is symmetric & second part is asymmetric Today we will briefly discuss about Green Gauss Theorem etc. Green Gauss Theorem relates the volume & surface integrals. The most common form of Gauss’s theorem is the Gauss divergence theorem which you have studied in previous courses. 푛 푣 ds If you have a volume U formed by surface S, the Gauss divergence theorem for a vector v suggest that v.. ndSˆ vdU SU where, S = bounding surface on closed surface U = volumetric domain nˆ = the unit outward normal vector of the elementary surface area ds This Gauss Divergence theorem can also be represented using index notations. v v n dS i dU ii SUxi For any scalar multiple or factor for vector v , say v , the Green Gauss can be represented as (v . nˆ ) dS .( v ) dU SU i.e. (v . nˆ ) dS ( . v ) dU ( v . ) dU SUU v or v n dSi dU v dU i i i SUUxxii Gauss’s theorem is applicable not only to a vector . It can be applied to any tensor B (say) B B n dSij dU B dU ij i ij SUUxxii Stoke’s Theorem Stoke’s theorem relates the integral over an open surface S, to line integral around the surface’s bounding curve (say C) You need to appropriately choose the unit outward normal vector to the surface 푛 푡 dr v.
    [Show full text]
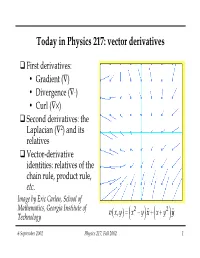
  • Today in Physics 217: Vector Derivatives
    Today in Physics 217: vector derivatives First derivatives: • Gradient (—) • Divergence (—◊) •Curl (—¥) Second derivatives: the Laplacian (—2) and its relatives Vector-derivative identities: relatives of the chain rule, product rule, etc. Image by Eric Carlen, School of Mathematics, Georgia Institute of 22 vxyxy, =−++ x yˆˆ x y Technology ()()() 6 September 2002 Physics 217, Fall 2002 1 Differential vector calculus df/dx provides us with information on how quickly a function of one variable, f(x), changes. For instance, when the argument changes by an infinitesimal amount, from x to x+dx, f changes by df, given by df df= dx dx In three dimensions, the function f will in general be a function of x, y, and z: f(x, y, z). The change in f is equal to ∂∂∂fff df=++ dx dy dz ∂∂∂xyz ∂∂∂fff =++⋅++ˆˆˆˆˆˆ xyzxyz ()()dx() dy() dz ∂∂∂xyz ≡⋅∇fdl 6 September 2002 Physics 217, Fall 2002 2 Differential vector calculus (continued) The vector derivative operator — (“del”) ∂∂∂ ∇ =++xyzˆˆˆ ∂∂∂xyz produces a vector when it operates on scalar function f(x,y,z). — is a vector, as we can see from its behavior under coordinate rotations: I ′ ()∇∇ff=⋅R but its magnitude is not a number: it is an operator. 6 September 2002 Physics 217, Fall 2002 3 Differential vector calculus (continued) There are three kinds of vector derivatives, corresponding to the three kinds of multiplication possible with vectors: Gradient, the analogue of multiplication by a scalar. ∇f Divergence, like the scalar (dot) product. ∇⋅v Curl, which corresponds to the vector (cross) product. ∇×v 6 September 2002 Physics 217, Fall 2002 4 Gradient The result of applying the vector derivative operator on a scalar function f is called the gradient of f: ∂∂∂fff ∇f =++xyzˆˆˆ ∂∂∂xyz The direction of the gradient points in the direction of maximum increase of f (i.e.
    [Show full text]
  • Divergence and Integral Tests Handout Reference: Brigg’S “Calculus: Early Transcendentals, Second Edition” Topics: Section 8.4: the Divergence and Integral Tests, P
    Lesson 17: Divergence and Integral Tests Handout Reference: Brigg's \Calculus: Early Transcendentals, Second Edition" Topics: Section 8.4: The Divergence and Integral Tests, p. 627 - 640 Theorem 8.8. p. 627 Divergence Test P If the infinite series ak converges, then lim ak = 0. k!1 P Equivalently, if lim ak 6= 0, then the infinite series ak diverges. k!1 Note: The divergence test cannot be used to conclude that a series converges. This test ONLY provides a quick mechanism to check for divergence. Definition. p. 628 Harmonic Series 1 1 1 1 1 1 The famous harmonic series is given by P = 1 + + + + + ··· k=1 k 2 3 4 5 Theorem 8.9. p. 630 Harmonic Series 1 1 The harmonic series P diverges, even though the terms of the series approach zero. k=1 k Theorem 8.10. p. 630 Integral Test Suppose the function f(x) satisfies the following three conditions for x ≥ 1: i. f(x) is continuous ii. f(x) is positive iii. f(x) is decreasing Suppose also that ak = f(k) for all k 2 N. Then 1 1 X Z ak and f(x)dx k=1 1 either both converge or both diverge. In the case of convergence, the value of the integral is NOT equal to the value of the series. Note: The Integral Test is used to determine whether a series converges or diverges. For this reason, adding or subtracting a finite number of terms in the series or changing the lower limit of the integration to another finite point does not change the outcome of the test.
    [Show full text]
  • Vector Calculus Applicationsž 1. Introduction 2. the Heat Equation
    Vector Calculus Applications 1. Introduction The divergence and Stokes’ theorems (and their related results) supply fundamental tools which can be used to derive equations which can be used to model a number of physical situations. Essentially, these theorems provide a mathematical language with which to express physical laws such as conservation of mass, momentum and energy. The resulting equations are some of the most fundamental and useful in engineering and applied science. In the following sections the derivation of some of these equations will be outlined. The goal is to show how vector calculus is used in applications. Generally speaking, the equations are derived by first using a conservation law in integral form, and then converting the integral form to a differential equation form using the divergence theorem, Stokes’ theorem, and vector identities. The differential equation forms tend to be easier to work with, particularly if one is interested in solving such equations, either analytically or numerically. 2. The Heat Equation Consider a solid material occupying a region of space V . The region has a boundary surface, which we shall designate as S. Suppose the solid has a density and a heat capacity c. If the temperature of the solid at any point in V is T.r; t/, where r x{ y| zkO is the position vector (so that T depends upon x, y, z and t), then theE total heatE eergyD O containedC O C in the solid is • cT dV : V Heat energy can get in or out of the region V by flowing across the boundary S, or it can be generated inside V .
    [Show full text]