DOCSLIB.ORG

Spherical Coordinates

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Spherical Coordinates Spherical Coordinates z r^ Transforms ^ " r The forward and reverse coordinate transformations are ! ^ ! r = x2 + y2 + z 2 r x = rsin! cos" y arctan" x2 y2 , z$ y r sin sin ! = # + % = ! " z = rcos! & = arctan(y,x) x " where we formally take advantage of the two argument arctan function to eliminate quadrant confusion. Unit Vectors The unit vectors in the spherical coordinate system are functions of position. It is convenient to express them in terms of the spherical coordinates and the unit vectors of the rectangular coordinate system which are not themselves functions of position. ! r xxˆ + yyˆ + zzˆ rˆ = = = xˆ sin! cos" + yˆ sin! sin " + zˆ cos! r r zˆ #rˆ "ˆ = = $ xˆ sin " + yˆ cos" sin! !ˆ = "ˆ # rˆ = xˆ cos! cos" + yˆ cos! sin " $ zˆ sin! Variations of unit vectors with the coordinates Using the expressions obtained above it is easy to derive the following handy relationships: !rˆ = 0 !r !rˆ = xˆ cos" cos# + yˆ cos" sin # $ zˆ sin " = "ˆ !" !rˆ = $xˆ sin" sin # + yˆ sin " cos# = ($ xˆ sin # + yˆ cos #)sin" = #ˆ sin" !# !"ˆ = 0 !r !"ˆ = 0 !# !"ˆ = $xˆ cos" $ yˆ sin " = $ rˆ sin # + #ˆ cos# !" ( ) !"ˆ = 0 !r !"ˆ = # xˆ sin " cos$ # yˆ sin" sin $ # zˆ cos" = #rˆ !" !"ˆ = # xˆ cos" sin $ + yˆ cos" cos$ = $ˆ cos" !$ Path increment ! We will have many uses for the path increment d r expressed in spherical coordinates: ! $ !rˆ !rˆ !rˆ ' dr = d(rrˆ ) = rˆ dr + rdrˆ = rˆ dr + r& dr + d" + d#) % !r !" !# ( = rˆ dr +"ˆ rd " + #ˆr sin "d# Time derivatives of the unit vectors We will also have many uses for the time derivatives of the unit vectors expressed in spherical coordinates: !rˆ !rˆ !rˆ rˆ˙ = r˙ + "˙ + #˙ = "ˆ " ˙ + #ˆ# ˙ sin " !r !" !# ˙ !"ˆ !"ˆ !"ˆ "ˆ = r˙ + "˙ + #˙ = $rˆ "˙ + #ˆ #˙ cos" !r !" !# ˙ !#ˆ !#ˆ !#ˆ #ˆ = r˙ + "˙ + #˙ = $ rˆ sin " + "ˆ cos" #˙ !r !" !# ( ) Velocity and Acceleration The velocity and acceleration of a particle may be expressed in spherical coordinates by taking into account the associated rates of change in the unit vectors: ! ˙! ˙ v = r = rˆ r + rˆ r˙ ! v rˆ r˙ ˆr ˙ ˆr ˙ sin = + ! ! + " " ! ! ! ˙ ˙ a = v˙ = rˆ˙ r˙ + rˆ ˙r˙ + !ˆr !˙ + !ˆr ˙ !˙ + !ˆr !˙˙ + "ˆr "˙ sin! + "ˆr ˙ "˙ sin! + "ˆ r "˙˙ sin ! + "ˆr "˙ ! ˙ cos! = (!ˆ! ˙ + "ˆ " ˙ sin!)r˙ + rˆ r˙˙ + (#rˆ !˙ + "ˆ" ˙ cos! )r!˙ + !ˆr ˙ !˙ + !ˆr !˙˙ + [#(rˆ sin! + !ˆ cos! )"˙ ]r"˙ sin ! + "ˆr ˙ "˙ sin ! + "ˆr "˙˙ sin ! + "ˆr "˙! ˙ cos! ! 2 2 2 2 a = rˆ "r"! r"" ! r#" sin " + "ˆ r"""+ 2r""" ! r#" sin" cos" + #ˆ r#""sin" + 2r""#" cos" + 2r"#" sin" ( ) ( ) ( ) The del operator from the definition of the gradient Any (static) scalar field u may be considered to be a function of the spherical coordinates r, θ, and φ. The value of u ! changes by an infinitesimal amount du when the point of observation is changed by d r . That change may be determined from the partial derivatives as !u !u !u du = dr + d" + d# . !r !" !# But we also define the gradient in such a way as to obtain the result ! ! du = !u " dr Therefore, !u !u !u ! ! dr + d" + d# = $u % dr ! r !" !# or, in spherical coordinates, !u !u !u ! ! ! dr + d" + d# = ($u ) dr + ($u ) rd" + ($ u) r sin"d# ! r !" !# r " # and we demand that this hold for any choice of dr, dθ, and dφ. Thus, ! "u ! 1 "u ! 1 "u !u = , !u = , !u = , ( )r r ( )# r ( )$ r sin " "# # "$ from which we find ! " #ˆ " $ˆ " ! = rˆ + + "r r "# rsin # "$ Divergence ! ! The divergence ! " A is carried out taking into account, once again, that the unit vectors themselves are functions of the coordinates. Thus, we have ! ˆ ˆ ! & # $ # % # ) ˆ ˆ ! " A = ( rˆ + + + " Ar rˆ + A $ + A % #r r #$ rsin $ #% ( $ % ) ' * where the derivatives must be taken before the dot product so that ! ! & # $ˆ # %ˆ # ) ! ! " A = ( rˆ + + + " A ' #r r #$ rsin $ #%* ! ! ! #A $ˆ #A %ˆ #A = rˆ " + " + " #r r #$ rsin$ #% & A ˆ ˆ ˆ ) #Ar #A$ ˆ # % ˆ #r #$ #% = rˆ " ( rˆ + $ + % + Ar + A$ + A% + ' #r #r #r #r #r #r * ˆ & #A ˆ ˆ ˆ ) $ #Ar ˆ #A$ ˆ % ˆ #r #$ #% + " ( r + $ + % + Ar + A$ + A% + r ' #$ #$ #$ #$ #$ #$ * ˆ & #A ˆ ˆ ˆ ) % #Ar #A$ ˆ % ˆ #r #$ #% + " ( rˆ + $ + % + Ar + A + A + r sin$ #% #% #% #% $ #% % #% ' * With the help of the partial derivatives previously obtained, we find ! ! A & #Ar #A$ ˆ # % ˆ ) ! " A = rˆ " ( rˆ + $ + % + 0 + 0 + 0+ ' #r #r #r * ˆ & #A #A ) $ #Ar ˆ $ ˆ % ˆ ˆ ˆ + " ( r + $ + % + Ar$ + A$ (,r ) + 0+ r ' #$ #$ #$ * ˆ A % & #Ar #A$ ˆ # % ˆ ˆ ˆ ˆ ) + " ( rˆ + $ + % + Ar sin$% + A$ cos$% + A% , rˆ sin $ + $ cos$ + r sin$ ' #% #% #% [ ( )]* A & #Ar ) & 1 #A$ Ar ) & 1 # % Ar A$ cos$ ) = ( + + ( + + + ( + + + ' #r * ' r #$ r * ' r sin$ #% r rsin $ * & #A 2A ) & 1 #A A cos$ ) 1 #A% = ( r + r + + ( $ + $ + + ' #r r * ' r #$ r sin$ * rsin $ #% ! ! 1 # 2 1 # 1 #A% ! " A = 2 (r Ar ) + (A$ sin$) + r #r rsin$ #$ r sin$ #% Curl ! ! The curl ! " A is also carried out taking into account that the unit vectors themselves are functions of the coordinates. Thus, we have ! ˆ ˆ ! & # $ # % # ) ˆ ˆ ! " A = ( rˆ + + + " Arrˆ + A $ + A % #r r #$ rsin $ #% ( $ % ) ' * where the derivatives must be taken before the cross product so that ! ! & # $ˆ # %ˆ # ) ! ! " A = ( rˆ + + + " A ' #r r #$ rsin $ #% * ! ! ! #A $ˆ #A %ˆ #A = rˆ " + " + " #r r #$ rsin $ #% & A ˆ ˆ ˆ ) #Ar #A$ ˆ # % ˆ #r #$ #% = rˆ " ( rˆ + $ + % + Ar + A$ + A% + ' #r #r #r #r #r #r* ˆ & #A ˆ ˆ ˆ ) $ #Ar ˆ #A$ ˆ % ˆ #r #$ #% + " ( r + $ + % + Ar + A$ + A% + r ' #$ #$ #$ #$ #$ #$ * ˆ & #A ˆ ˆ ˆ ) % #Ar #A$ ˆ % ˆ #r #$ #% + " ( rˆ + $ + % + Ar + A + A + r sin$ #% #% #% #% $ #% % #% ' * With the help of the partial derivatives previously obtained, we find ! ! & #A ) #Ar #A$ ˆ % ˆ ! " A = rˆ " ( rˆ + $ + % + 0 + 0 + 0+ ' #r #r #r * ˆ #A $ & #Ar #A$ ˆ % ˆ ˆ ) + " ( rˆ + $ + % + Ar$ + A$ (,rˆ ) + 0+ r ' #$ #$ #$ * ˆ #A % & #Ar #A$ ˆ % ˆ ˆ ˆ ˆ ) + " ( rˆ + $ + % + Ar sin $% + A$ cos$% + A% , rˆ sin$ + $ cos$ + r sin$ ' #% #% #% [ ( )]* A A & #A$ ˆ # % ˆ) & 1 #Ar ˆ 1 # % A$ ˆ) = ( % , $ + + ( , % + rˆ + %+ ' #r #r * ' r #$ r #$ r * A A cos & 1 #Ar ˆ 1 #A$ % ˆ % $ ) + ( $ , rˆ , $ + rˆ + ' r sin$ #% r sin$ #% r r sin$ * A A cos & 1 # % 1 #A$ % $ ) = rˆ ( , + + ' r #$ r sin$ #% rsin $ * A A ˆ & # % 1 #Ar % ) + $ ( , + , + ' #r rsin $ #% r * & #A 1 #A A ) + %ˆ ( $ , r + $ + ' #r r #$ r * ! ! ˆ ˆ ˆ r ' $ $A# * # ' $Ar $ * % ' $ $Ar * ! " A = A% sin# & + & sin # rA% + (rA# ) & r sin# ) $# ( ) $% , rsin # ) $% $r ( ), r () $r $# +, ( + ( + Laplacian The Laplacian is a scalar operator that can be determined from its definition as ! ! ˆ ˆ ˆ ˆ 2 & # $ # % # ) & #u $ #u % #u) ! u = ! " (!u ) = ( rˆ + + + " ( rˆ + + + ' #r r #$ rsin $ #%* ' #r r #$ r sin$ #% * # & #u $ˆ #u %ˆ #u) = rˆ " ( rˆ + + + #r ' #r r #$ rsin $ #% * $ˆ # & #u $ˆ #u %ˆ #u ) + " ( rˆ + + + r #$ ' #r r #$ rsin $ #% * %ˆ # & #u $ˆ #u %ˆ #u) + " ( rˆ + + + rsin $ #% #r r #$ r sin$ #% ' * With the help of the partial derivatives previously obtained, we find 2 ˆ ˆ 2 ˆ ˆ 2 2 ' # u % #u % # u & #u & # u * ! u = rˆ ") rˆ 2 $ 2 + $ 2 + , ( #r r #% r #%#r r sin % #& r sin% #&#r + ˆ 2 ˆ 2 ˆ ˆ 2 % ' ˆ #u # u rˆ #u % # u & cos% #u & # u * + " ) % + rˆ $ + 2 $ 2 + , r ( #r #r#% r #% r #% r sin % #& rsin % #&#% + ˆ 2 ˆ ˆ 2 ˆ ˆ 2 & ' ˆ #u # u & cos% #u % # u rˆ sin % + % cos% #u & # u * + " ) & sin % + rˆ + + $ + , rsin % #r #r#& r #% r #%#& rsin % #& rsin % #&2 ( + ' # 2u* ' 1 #u 1 # 2u* ' 1 #u cos% #u 1 # 2u * = ) 2 , + ) + 2 2 , + ) + 2 + 2 2 2 , ( #r + ( r #r r #% + ( r #r r sin % #% r sin % #& + ' # 2u 2 #u* ' 1 # 2u cos% #u * ' 1 # 2u* = ) 2 + , + ) 2 2 + 2 , + ) 2 2 2 , ( #r r #r + ( r #% r sin % #% + ( r sin % #& + 1 # ' #u* 1 # ' #u* 1 # 2u = ) r 2 , + ) sin % , + r 2 #r ( #r + r 2 sin% #% ( #% + r2 sin 2 % #&2 Thus, the Laplacian operator can be written as 2 2 1 " # 2 " & 1 " # " & 1 " ! = % r ( + % sin ) ( + r 2 "r $ "r ' r 2 sin) ") $ ") ' r2 sin2 ) "*2.
Load more

Recommended publications
  • College Summit, Inc. D/B/A Peerforward Financial Statements
    College Summit, Inc. d/b/a PeerForward Financial Statements For the Years Ended April 30, 2020 and 2019 and Report Thereon COLLEGE SUMMIT, INC. d/b/a PeerForward TABLE OF CONTENTS For the Years Ended April 30, 2020 and 2019 _______________ Page Independent Auditors’ Report ............................................................................................................. 1-2 Financial Statements Statements of Financial Position ........................................................................................................ 3 Statements of Activities ...................................................................................................................... 4 Statements of Functional Expenses ................................................................................................ 5-6 Statements of Cash Flows .................................................................................................................. 7 Notes to Financial Statements ....................................................................................................... 8-17 INDEPENDENT AUDITORS’ REPORT To the Board of Directors of College Summit, Inc. d/b/a PeerForward Report on the Financial Statements We have audited the accompanying financial statements of College Summit, Inc. d/b/a PeerForward (PeerForward), which comprise the statements of financial position as of April 30, 2020 and 2019, and the related statements of activities, functional expenses and cash flows for the years then ended, and the related notes
    [Show full text]
  • How Can We Create Environments Where Hate Cannot Flourish?
    How can we create environments where hate cannot flourish? Saturday, February 1 9:30 a.m. – 10:00 a.m. Check-In and Registration Location: Field Museum West Entrance 10:00 a.m. – 10:30 a.m. Introductions and Program Kick-Off JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 10:30 a.m. – 11:30 a.m. Watch “The Path to Nazi Genocide” and Reflections JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1 11:30 a.m. – 11:45 a.m. Break and walk to State of Deception 11:45 a.m. – 12:30 p.m. Visit State of Deception Interpretation by Holocaust Survivor Volunteers from the Illinois Holocaust Museum Location: Upper level 12:30 p.m. – 1:00 p.m. Breakout Session: Reflections on Exhibit Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B Saturday, February 2 (continued) 1:00 p.m. – 1:45 p.m. Lunch 1:45 p.m. – 2:45 p.m. A Survivor’s Personal Story Bob Behr, USHMM Survivor Volunteer Interviewed by: Ann Weber, USHMM Program Coordinator Location: Lecture Hall 1 2:45 p.m. – 3:00 p.m. Break 3:00 p.m. – 3:45 p.m. Student Panel: Beyond Indifference Location: Lecture Hall 1 Moderator: Emma Pettit, Sustained Dialogue Campus Network Student/Alumni Panelists: Jazzy Johnson, Northwestern University Mary Giardina, The Ohio State University Nory Kaplan-Kelly, University of Chicago 3:45 p.m. – 4:30 p.m. Breakout Session: Sharing Personal Reflections Tim Kaiser, USHMM Director, Education Initiatives David Klevan, USHMM Digital Learning Strategist JoAnna Wasserman, USHMM Education Initiatives Manager Location: Lecture Hall 1, Classrooms A and B 4:30 p.m.
    [Show full text]
  • 1 Curl and Divergence
    Sections 15.5-15.8: Divergence, Curl, Surface Integrals, Stokes' and Divergence Theorems Reeve Garrett 1 Curl and Divergence Definition 1.1 Let F = hf; g; hi be a differentiable vector field defined on a region D of R3. Then, the divergence of F on D is @ @ @ div F := r · F = ; ; · hf; g; hi = f + g + h ; @x @y @z x y z @ @ @ where r = h @x ; @y ; @z i is the del operator. If div F = 0, we say that F is source free. Note that these definitions (divergence and source free) completely agrees with their 2D analogues in 15.4. Theorem 1.2 Suppose that F is a radial vector field, i.e. if r = hx; y; zi, then for some real number p, r hx;y;zi 3−p F = jrjp = (x2+y2+z2)p=2 , then div F = jrjp . Theorem 1.3 Let F = hf; g; hi be a differentiable vector field defined on a region D of R3. Then, the curl of F on D is curl F := r × F = hhy − gz; fz − hx; gx − fyi: If curl F = 0, then we say F is irrotational. Note that gx − fy is the 2D curl as defined in section 15.4. Therefore, if we fix a point (a; b; c), [gx − fy](a; b; c), measures the rotation of F at the point (a; b; c) in the plane z = c. Similarly, [hy − gz](a; b; c) measures the rotation of F in the plane x = a at (a; b; c), and [fz − hx](a; b; c) measures the rotation of F in the plane y = b at the point (a; b; c).
    [Show full text]
  • Stroke Training for EMS Professionals (PDF)
    STROKE TRAINING FOR EMS PROFESSIONALS 1 COURSE OBJECTIVES About Stroke Stroke Policy Recommendations Stroke Protocols and Stroke Hospital Care Stroke Assessment Tools Pre-Notification Stroke Treatment ABOUT STROKE STROKE FACTS • A stroke is a medical emergency! Stroke occurs when blood flow is either cut off or is reduced, depriving the brain of blood and oxygen • Approximately 795,000 strokes occur in the US each year • Stroke is the fifth leading cause of death in the US • Stroke is a leading cause of adult disability • On average, every 40 seconds, someone in the United States has a stroke • Over 4 million stroke survivors are in the US • The indirect and direct cost of stroke: $38.6 billion annually (2009) • Crosses all ethnic, racial and socioeconomic groups Berry, Jarett D., et al. Heart Disease and Stroke Statistics --2013 Update: A Report from the American Heart Association. Circulation. 127, 2013. DIFFERENT TYPES OF STROKE Ischemic Stroke • Caused by a blockage in an artery stopping normal blood and oxygen flow to the brain • 87% of strokes are ischemic • There are two types of ischemic strokes: Embolism: Blood clot or plaque fragment from elsewhere in the body gets lodged in the brain Thrombosis: Blood clot formed in an artery that provides blood to the brain Berry, Jarett D., et al. Heart Disease and Stroke Statistics --2013 Update: A Report from the American Heart Association. Circulation. 127, 2013. http://www.strokeassociation.org/STROKEORG/AboutStroke/TypesofStroke/IschemicClots/Ischemic-Strokes- Clots_UCM_310939_Article.jsp
    [Show full text]
  • Symmetry and Tensors Rotations and Tensors
    Symmetry and tensors Rotations and tensors A rotation of a 3-vector is accomplished by an orthogonal transformation. Represented as a matrix, A, we replace each vector, v, by a rotated vector, v0, given by multiplying by A, 0 v = Av In index notation, 0 X vm = Amnvn n Since a rotation must preserve lengths of vectors, we require 02 X 0 0 X 2 v = vmvm = vmvm = v m m Therefore, X X 0 0 vmvm = vmvm m m ! ! X X X = Amnvn Amkvk m n k ! X X = AmnAmk vnvk k;n m Since xn is arbitrary, this is true if and only if X AmnAmk = δnk m t which we can rewrite using the transpose, Amn = Anm, as X t AnmAmk = δnk m In matrix notation, this is t A A = I where I is the identity matrix. This is equivalent to At = A−1. Multi-index objects such as matrices, Mmn, or the Levi-Civita tensor, "ijk, have definite transformation properties under rotations. We call an object a (rotational) tensor if each index transforms in the same way as a vector. An object with no indices, that is, a function, does not transform at all and is called a scalar. 0 A matrix Mmn is a (second rank) tensor if and only if, when we rotate vectors v to v , its new components are given by 0 X Mmn = AmjAnkMjk jk This is what we expect if we imagine Mmn to be built out of vectors as Mmn = umvn, for example. In the same way, we see that the Levi-Civita tensor transforms as 0 X "ijk = AilAjmAkn"lmn lmn 1 Recall that "ijk, because it is totally antisymmetric, is completely determined by only one of its components, say, "123.
    [Show full text]
  • A Brief Tour of Vector Calculus
    A BRIEF TOUR OF VECTOR CALCULUS A. HAVENS Contents 0 Prelude ii 1 Directional Derivatives, the Gradient and the Del Operator 1 1.1 Conceptual Review: Directional Derivatives and the Gradient........... 1 1.2 The Gradient as a Vector Field............................ 5 1.3 The Gradient Flow and Critical Points ....................... 10 1.4 The Del Operator and the Gradient in Other Coordinates*............ 17 1.5 Problems........................................ 21 2 Vector Fields in Low Dimensions 26 2 3 2.1 General Vector Fields in Domains of R and R . 26 2.2 Flows and Integral Curves .............................. 31 2.3 Conservative Vector Fields and Potentials...................... 32 2.4 Vector Fields from Frames*.............................. 37 2.5 Divergence, Curl, Jacobians, and the Laplacian................... 41 2.6 Parametrized Surfaces and Coordinate Vector Fields*............... 48 2.7 Tangent Vectors, Normal Vectors, and Orientations*................ 52 2.8 Problems........................................ 58 3 Line Integrals 66 3.1 Defining Scalar Line Integrals............................. 66 3.2 Line Integrals in Vector Fields ............................ 75 3.3 Work in a Force Field................................. 78 3.4 The Fundamental Theorem of Line Integrals .................... 79 3.5 Motion in Conservative Force Fields Conserves Energy .............. 81 3.6 Path Independence and Corollaries of the Fundamental Theorem......... 82 3.7 Green's Theorem.................................... 84 3.8 Problems........................................ 89 4 Surface Integrals, Flux, and Fundamental Theorems 93 4.1 Surface Integrals of Scalar Fields........................... 93 4.2 Flux........................................... 96 4.3 The Gradient, Divergence, and Curl Operators Via Limits* . 103 4.4 The Stokes-Kelvin Theorem..............................108 4.5 The Divergence Theorem ...............................112 4.6 Problems........................................114 List of Figures 117 i 11/14/19 Multivariate Calculus: Vector Calculus Havens 0.
    [Show full text]
  • Curl, Divergence and Laplacian
    Curl, Divergence and Laplacian What to know: 1. The definition of curl and it two properties, that is, theorem 1, and be able to predict qualitatively how the curl of a vector field behaves from a picture. 2. The definition of divergence and it two properties, that is, if div F~ 6= 0 then F~ can't be written as the curl of another field, and be able to tell a vector field of clearly nonzero,positive or negative divergence from the picture. 3. Know the definition of the Laplace operator 4. Know what kind of objects those operator take as input and what they give as output. The curl operator Let's look at two plots of vector fields: Figure 1: The vector field Figure 2: The vector field h−y; x; 0i: h1; 1; 0i We can observe that the second one looks like it is rotating around the z axis. We'd like to be able to predict this kind of behavior without having to look at a picture. We also promised to find a criterion that checks whether a vector field is conservative in R3. Both of those goals are accomplished using a tool called the curl operator, even though neither of those two properties is exactly obvious from the definition we'll give. Definition 1. Let F~ = hP; Q; Ri be a vector field in R3, where P , Q and R are continuously differentiable. We define the curl operator: @R @Q @P @R @Q @P curl F~ = − ~i + − ~j + − ~k: (1) @y @z @z @x @x @y Remarks: 1.
    [Show full text]
  • Medical Terminology Abbreviations Medical Terminology Abbreviations
    34 MEDICAL TERMINOLOGY ABBREVIATIONS MEDICAL TERMINOLOGY ABBREVIATIONS The following list contains some of the most common abbreviations found in medical records. Please note that in medical terminology, the capitalization of letters bears significance as to the meaning of certain terms, and is often used to distinguish terms with similar acronyms. @—at A & P—anatomy and physiology ab—abortion abd—abdominal ABG—arterial blood gas a.c.—before meals ac & cl—acetest and clinitest ACLS—advanced cardiac life support AD—right ear ADL—activities of daily living ad lib—as desired adm—admission afeb—afebrile, no fever AFB—acid-fast bacillus AKA—above the knee alb—albumin alt dieb—alternate days (every other day) am—morning AMA—against medical advice amal—amalgam amb—ambulate, walk AMI—acute myocardial infarction amt—amount ANS—automatic nervous system ant—anterior AOx3—alert and oriented to person, time, and place Ap—apical AP—apical pulse approx—approximately aq—aqueous ARDS—acute respiratory distress syndrome AS—left ear ASA—aspirin asap (ASAP)—as soon as possible as tol—as tolerated ATD—admission, transfer, discharge AU—both ears Ax—axillary BE—barium enema bid—twice a day bil, bilateral—both sides BK—below knee BKA—below the knee amputation bl—blood bl wk—blood work BLS—basic life support BM—bowel movement BOW—bag of waters B/P—blood pressure bpm—beats per minute BR—bed rest MEDICAL TERMINOLOGY ABBREVIATIONS 35 BRP—bathroom privileges BS—breath sounds BSI—body substance isolation BSO—bilateral salpingo-oophorectomy BUN—blood, urea, nitrogen
    [Show full text]
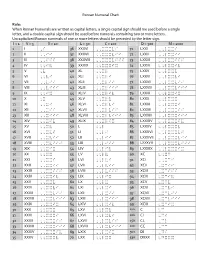
  • Roman Numeral Chart
    Roman Numeral Chart Rule: When Roman Numerals are written as capital letters, a single capital sign should me used before a single letter, and a double capital sign should be used before numerals containing two or more letters. Uncapitalized Roman numerals of one or more letters should be preceded by the letter sign. I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1000 1 I ,I 36 XXXVI ,,XXXVI 71 LXXI ,,LXXI 2 II ,,II 37 XXXVII ,,XXXVII 72 LXXII ,,LXXII 3 III ,,III 38 XXXVIII ,,XXXVIII 73 LXXIII ,,LXXIII 4 IV ,,IV 39 XXXIX ,,XXXIX 74 LXXIV ,,LXXIV 5 V ,V 40 XL ,,XL 75 LXXV ,,LXXV 6 VI ,,VI 41 XLI ,,XLI 76 LXXVI ,,LXXVI 7 VII ,,VII 42 XLII ,,XLII 77 LXXVII ,,LXXVII 8 VIII ,,VIII 43 XLIII ,,XLIII 78 LXXVIII ,,LXXVIII 9 IX ,,IX 44 XLIV ,,XLIV 79 LXXIX ,,LXXIX 10 X ,X 45 XLV ,,XLV 80 LXXX ,,LXXX 11 XI ,,XI 46 XLVI ,,XLVI 81 LXXXI ,,LXXXI 12 XII ,,XII 47 XLVII ,,XLVII 82 LXXXII ,,LXXXII 13 XIII ,,XIII 48 XLVIII ,,XLVIII 83 LXXXIII ,,LXXXIII 14 XIV ,,XIV 49 XLIX ,,XLIX 84 LXXXIV ,,LXXXIV 15 XV ,,XV 50 L ,,L 85 LXXXV ,,LXXXV 16 XVI ,,XVI 51 LI ,,LI 86 LXXXVI ,,LXXXVI 17 XVII ,,XVII 52 LII ,,LII 87 LXXXVII ,,LXXXVII 18 XVIII ,,XVIII 53 LIII ,,LIII 88 LXXXVIII ,,LXXXVIII 19 XIX ,,XIX 54 LIV ,,LIV 89 LXXXIX ,,LXXXIX 20 XX ,,XX 55 LV ,,LV 90 XC ,,XC 21 XXI ,,XXI 56 LVI ,,LVI 91 XCI ,,XCI 22 XXII ,,XXII 57 LVII ,,LVII 92 XCII ,XCII 23 XXIII ,,XXIII 58 LVIII ,,LVIII 93 XCIII ,XCIII 24 XXIV ,,XXIV 59 LIX ,,LIX 94 XCIV ,XCIV 25 XXV ,,XXV 60 LX ,,LX 95 XCV ,XCV 26 XXVI ,,XXVI 61 LXI ,,LXI 96 XCVI ,XCVI 27 XXVII ,,XXVII 62 LXII ,,LXII 97 XCVII ,XCVII 28 XXVIII ,,XXVIII 63 LXIII ,,LXIII 98 XCVIII ,XCVIII 29 XXIX ,,XXIX 64 LXIV ,,LXIV 99 XCIX ,XCIX 30 XXX ,,XXX 65 LXV ,,LXV 100 C ,C 31 XXXI ,,XXXI 66 LXVI ,,LXVI 101 CI ,CI 32 XXXII ,,XXXII 67 LXVII ,,LXVII 150 CL ,CL 33 XXXIII ,,XXXIII 68 LXVIII ,,LXVIII 200 CC ,CC 34 XXXIV ,,XXXIV 69 LXIX ,,LXIX 501 DI ,DI 35 XXXV ,,XXXV 70 LXX ,,LXX 530 DXXX ,DXXX .
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • 10A– Three Generalizations of the Fundamental Theorem of Calculus MATH 22C
    10A– Three Generalizations of the Fundamental Theorem of Calculus MATH 22C 1. Introduction In the next four sections we present applications of the three generalizations of the Fundamental Theorem of Cal- culus (FTC) to three space dimensions (x, y, z) 3,a version associated with each of the three linear operators,2R the Gradient, the Curl and the Divergence. Since much of classical physics is framed in terms of these three gener- alizations of FTC, these operators are often referred to as the three linear first order operators of classical physics. The FTC in one dimension states that the integral of a function over a closed interval [a, b] is equal to its anti- derivative evaluated between the endpoints of the interval: b f 0(x)dx = f(b) f(a). − Za This generalizes to the following three versions of the FTC in two and three dimensions. The first states that the line integral of a gradient vector field F = f along a curve , (in physics the work done by F) is exactlyr equal to the changeC in its potential potential f across the endpoints A, B of : C F Tds= f(B) f(A). (1) · − ZC The second, called Stokes Theorem, says that the flux of the Curl of a vector field F through a two dimensional surface in 3 is the line integral of F around the curve that S R 1 C 2 bounds : S CurlF n dσ = F Tds (2) · · ZZS ZC And the third, called the Divergence Theorem, states that the integral of the Divergence of F over an enclosed vol- ume is equal to the flux of F outward through the two dimensionalV closed surface that bounds : S V DivF dV = F n dσ.
    [Show full text]
  • The Divergence of a Vector Field.Doc 1/8
    9/16/2005 The Divergence of a Vector Field.doc 1/8 The Divergence of a Vector Field The mathematical definition of divergence is: w∫∫ A(r )⋅ds ∇⋅A()rlim = S ∆→v 0 ∆v where the surface S is a closed surface that completely surrounds a very small volume ∆v at point r , and where ds points outward from the closed surface. From the definition of surface integral, we see that divergence basically indicates the amount of vector field A ()r that is converging to, or diverging from, a given point. For example, consider these vector fields in the region of a specific point: ∆ v ∆v ∇⋅A ()r0 < ∇ ⋅>A (r0) Jim Stiles The Univ. of Kansas Dept. of EECS 9/16/2005 The Divergence of a Vector Field.doc 2/8 The field on the left is converging to a point, and therefore the divergence of the vector field at that point is negative. Conversely, the vector field on the right is diverging from a point. As a result, the divergence of the vector field at that point is greater than zero. Consider some other vector fields in the region of a specific point: ∇⋅A ()r0 = ∇ ⋅=A (r0) For each of these vector fields, the surface integral is zero. Over some portions of the surface, the normal component is positive, whereas on other portions, the normal component is negative. However, integration over the entire surface is equal to zero—the divergence of the vector field at this point is zero. * Generally, the divergence of a vector field results in a scalar field (divergence) that is positive in some regions in space, negative other regions, and zero elsewhere.
    [Show full text]