Reliability Optimization of a Railway Network
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Economic Overview and Opportunities of Shandong Province
ECONOMIC OVERVIEW AND OPPORTUNITIES OF SHANDONG PROVINCE ECONOMIC OVERVIEW AND OPPORTUNITIES OF SHANDONG PROVINCE ECONOMIC OVERVIEW AND OPPORTUNITIES OF SHANDONG PROVINCE 2 ECONOMIC OVERVIEW AND OPPORTUNITIES OF SHANDONG PROVINCE December 2016 NETHERLANDS BUSINESS SUPPORT OFFICE JINAN & QINGDAO Mr. Roland Brouwer (Chief Representative NBSO Jinan & Qingdao) Mr. Peng Liu (Deputy Representative NBSO Jinan) Ms. Sarah Xiao (Deputy Representative NBSO Qingdao) Ms. Xiaoming Liu (Commercial Assistant NBSO Jinan & Qingdao) Cover photo: night view of Qingdao coastline This report is part of a series of economic overviews of important regions in China1, initiated and developed by the Netherlands Economic Network in China. For more information about the Netherlands economic network and its publications, please visit www.zakendoeninchina.org or contact the Dutch embassy in Beijing at [email protected]. Unauthorized use, disclosure or copying without permission of the publisher is strictly prohibited. The information contained herein, including any expression of opinion, analyses, charting or tables, and statistics has been obtained from or is based upon sources believed to be reliable but is not guaranteed as to accuracy or completeness. 1 The composers of this document have done their best to credit the rightful sources of the data and images used. If, despite the efforts there still are sources not authorized, they are invited to contact [email protected] and [email protected]. 3 ECONOMIC OVERVIEW AND OPPORTUNITIES OF SHANDONG PROVINCE CONTENTS This report provides an overview of the economy of China’s coastal province Shandong; what it is today and in which direction it is heading. We introduce both key cities in Shandong and the roles they play in Shandong’s economy and main industries. -

Emperor's River: China's Grand Canal – Philipp Scholz Rittermann July 1
Emperor’s River: China’s Grand Canal – Philipp Scholz Rittermann July 1 – November 30, 2014 Harn Museum of Art -- Rubin Gallery Introduction In 2009 and 2010, photographer Philipp Scholz Rittermann traveled along China’s Grand Canal to capture the country’s booming economy, and rapidly changing landscape and social structure. Rittermann’s photographic interests are largely focused on the built environment, and the way people and the planet are transformed by it. He traveled to China first as an invited artist and then on succeeding trips to document this massive waterway. Having mastered, in previous projects, the digital panorama—a format hungry for information—he found his ideal subject in the People’s Republic of China. The number of bridges, boats, scooters, railways, and the subject of the series itself, the Grand Canal, speaks to Rittermann’s fascination with passage. This material manifestation of movement becomes symbolic of our collective human journey in the 21st century. Accelerated passage and progress are the means by which this particular culture, China, and subsequently the world, plunges headlong into the future. Rittermann wants to momentarily arrest these unprecedented changes to reflect on their ramifications. As we voyage out of one century into another, his photographs become lyrical topographical maps from which to chart the course of a brave new world. — Carol McCusker, Curator About the Artist & Series To make his photographs, Philipp Rittermann handholds a digital camera, panning across a scene, making exposures every few seconds, anticipating what is about to happen in each frame. The specific needs of each frame (light, perspective, focal separation) must be understood in a fraction of a second while shooting. -

Annual Report Annual Report 2020
2020 Annual Report Annual Report 2020 For further details about information disclosure, please visit the website of Yanzhou Coal Mining Company Limited at Important Notice The Board, Supervisory Committee and the Directors, Supervisors and senior management of the Company warrant the authenticity, accuracy and completeness of the information contained in the annual report and there are no misrepresentations, misleading statements contained in or material omissions from the annual report for which they shall assume joint and several responsibilities. The 2020 Annual Report of Yanzhou Coal Mining Company Limited has been approved by the eleventh meeting of the eighth session of the Board. All ten Directors of quorum attended the meeting. SHINEWING (HK) CPA Limited issued the standard independent auditor report with clean opinion for the Company. Mr. Li Xiyong, Chairman of the Board, Mr. Zhao Qingchun, Chief Financial Officer, and Mr. Xu Jian, head of Finance Management Department, hereby warrant the authenticity, accuracy and completeness of the financial statements contained in this annual report. The Board of the Company proposed to distribute a cash dividend of RMB10.00 per ten shares (tax inclusive) for the year of 2020 based on the number of shares on the record date of the dividend and equity distribution. The forward-looking statements contained in this annual report regarding the Company’s future plans do not constitute any substantive commitment to investors and investors are reminded of the investment risks. There was no appropriation of funds of the Company by the Controlling Shareholder or its related parties for non-operational activities. There were no guarantees granted to external parties by the Company without complying with the prescribed decision-making procedures. -

Federal Register/Vol. 86, No. 119/Thursday, June 24, 2021/Notices
33222 Federal Register / Vol. 86, No. 119 / Thursday, June 24, 2021 / Notices MPROVE Co., Limited Shanghai Jade Shuttle Hardware Tools Co., Wire Products Manufacturing Co., Ltd. Nailtech Co., Ltd. Ltd. Wuhu Diamond Metal Products Co., ltd Nanjing Duraturf Co., Ltd. Shanghai March Import & Export Co., Ltd. Wulian Zhanpeng Metals Co., Ltd. Nanjing Nuochun Hardware Co., Ltd. Shanghai Seti Enterprise Int’l Co., Ltd. Wuxi Holtrent International Co., Ltd. Nanjing Tianxingtong Electronic Technology Shanghai Shenda Imp. & Exp. Co., Ltd Wuxi Yushea Furniture Co., Ltd. Co., Ltd. Shanghai Sutek Industries Co., Ltd. Xiamen Hongju Printing Industry &trade Co., Nanjing Tianyu International Co., Ltd. Shanghai Television and Electronics Import Ltd. Nanjing Toua Hardware & Tools Co., Ltd. and Export Co., Ltd. Xuzhou Cip International Group Co, Ltd. Nanjing Zeejoe International Trade Shanghai Yiren Machinery Co., Ltd. Yiwu Competency Trading Co., Ltd. Nantong Intlevel Trade Co., Ltd. Shanghai Yueda Fasteners Co., Ltd. Yiwu Kingland Import & Export Co. Natuzzi China Limited Shanghai Zoonlion Industrial Co., Limited Yiwu Taisheng Decoration Materials Limited Nielsen Bainbridge LLC Shanghai Zoonlion Industrial Co., Ltd. Yiwu Yipeng Import & Export Co., Ltd. Ningbo Adv. Tools Co., Ltd. Shanxi Easyfix Trade Co., Ltd. Yongchang Metal Product Co., Ltd. Ningbo Angelstar Trading Co., Ltd. Shanxi Fastener & Hardware Products Youngwoo Fasteners Co., Ltd. Ningbo Bright Max Co., Ltd. Shanxi Xinjintai Hardware Co., Ltd. Yuyao Dingfeng Engineering Co. Ltd. Ningbo Fine Hardware Production Co., Ltd. Shaoxing Bohui Import and Export Co., Ltd Zhanghaiding Hardware Co., Ltd. Ningbo Freewill Imp. & Exp. Co., Ltd. Shaoxing Chengye Metal Producing Co., Ltd. Zhangjiagang Lianfeng Metals Products Co., Ningbo Home-dollar Imp.& Exp. -

Insar Reveals Land Deformation at Guangzhou and Foshan, China Between 2011 and 2017 with COSMO-Skymed Data
remote sensing Article InSAR Reveals Land Deformation at Guangzhou and Foshan, China between 2011 and 2017 with COSMO-SkyMed Data Alex Hay-Man Ng 1,2 ID , Hua Wang 1,*, Yiwei Dai 1, Carolina Pagli 3, Wenbin Chen 1, Linlin Ge 2, Zheyuan Du 2 and Kui Zhang 4 1 Department of Surveying Engineering, Guangdong University of Technology, Guangzhou 510006, China; [email protected] (A.H.-M.N.); [email protected] (Y.D.); [email protected] (W.C.) 2 School of Civil and Environmental Engineering, UNSW Australia, Sydney 2052, Australia; [email protected] (L.G.); [email protected] (Z.D.) 3 Department of Earth Sciences, University of Pisa, Pisa 56100, Italy; [email protected] 4 School of Communication Engineering, Chongqing University, Chongqing 400044, China; [email protected] * Correspondence: [email protected]; Tel.: +86-135-7001-9257 Received: 23 April 2018; Accepted: 23 May 2018; Published: 24 May 2018 Abstract: Subsidence from groundwater extraction and underground tunnel excavation has been known for more than a decade in Guangzhou and Foshan, but past studies have only monitored the subsidence patterns as far as 2011 using InSAR. In this study, the deformation occurring during the most recent time-period between 2011 and 2017 has been measured using COSMO-SkyMed (CSK) to understand if changes in temporal and spatial patterns of subsidence rates occurred. Using InSAR time-series analysis (TS-InSAR), we found that significant surface displacement rates occurred in the study area varying from −35 mm/year (subsidence) to 10 mm/year (uplift). The 2011–2017 TS-InSAR results were compared to two separate TS-InSAR analyses (2011–2013, and 2013–2017). -

China Railway Signal & Communication Corporation
Hong Kong Exchanges and Clearing Limited and The Stock Exchange of Hong Kong Limited take no responsibility for the contents of this announcement, make no representation as to its accuracy or completeness and expressly disclaim any liability whatsoever for any loss howsoever arising from or in reliance upon the whole or any part of the contents of this announcement. China Railway Signal & Communication Corporation Limited* 中國鐵路通信信號股份有限公司 (A joint stock limited liability company incorporated in the People’s Republic of China) (Stock Code: 3969) ANNOUNCEMENT ON BID-WINNING OF IMPORTANT PROJECTS IN THE RAIL TRANSIT MARKET This announcement is made by China Railway Signal & Communication Corporation Limited* (the “Company”) pursuant to Rules 13.09 and 13.10B of the Rules Governing the Listing of Securities on The Stock Exchange of Hong Kong Limited (the “Listing Rules”) and the Inside Information Provisions (as defined in the Listing Rules) under Part XIVA of the Securities and Futures Ordinance (Chapter 571 of the Laws of Hong Kong). From July to August 2020, the Company has won the bidding for a total of ten important projects in the rail transit market, among which, three are acquired from the railway market, namely four power integration and the related works for the CJLLXZH-2 tender section of the newly built Langfang East-New Airport intercity link (the “Phase-I Project for the Newly-built Intercity Link”) with a tender amount of RMB113 million, four power integration and the related works for the XJSD tender section of the newly built -

Supply Chain Strategic Alliances Partner Selection for Rizhao Port
International Journal of Scientific and Research Publications, Volume 4, Issue 11, November 2014 1 ISSN 2250-3153 Supply Chain Strategic Alliances Partner Selection for Rizhao Port Libin Guo School of Management, Qufu Normal University,Rizhao276826,China Abstract- Under the background of port supply chain strategic alliances,we clarify the current situation of Rizhao Port by SWOT analysis and find out the ST strategy for it, furthermore, we screen out the optimal cooperation partner for Rizhao Port under different alliance forms range from horizontal integration and vertical integration to the blended dynamic logistics alliance. Index Terms- Port Supply Chain; the SWOT Analysis; RiZhao Port; Strategical alliance I. INTRODUCTION ort supply chain, a main constituent of port logistics, includes the levels such as informationization, automation and networking, P and emphasizes the modern management of material transportation chain of each link and the extension of comprehensive services.Meanwhile, due to the connection between ports and suppliers and consumers all over the world through shippping companies and land forwarding agents, a port supply chain integrating many means1 of transportation and types of logistics is formed, and it becomes a relatively best main part and link for the coordinated management of supply chain. Therefore, we can start from the analysis of the SWOT of Rizhao port supply chain, and find out the cooperative partners suitable for the strategical alliance of Rizhao port supply chain among different types of alliance. II. THE SWOT ANALYSIS OF RIZHAO PORT SUPPLY CHAIN The SWOT analysis, a commonly used method of strategic competition, is based on analyzing the internal conditions of enterprises itself, and finds out the strengths, weaknesses and core competence. -

Land-Use Efficiency in Shandong (China)
sustainability Article Land-Use Efficiency in Shandong (China): Empirical Analysis Based on a Super-SBM Model Yayuan Pang and Xinjun Wang * Department of Environmental Science and Engineering, Fudan University, Shanghai 200433, China; [email protected] * Correspondence: [email protected] Received: 20 November 2020; Accepted: 14 December 2020; Published: 18 December 2020 Abstract: A reasonable evaluation of land-use efficiency is an important issue in land use and development. By using a super-SBM model, the construction and cultivated land-use efficiency of 17 cities in Shandong from 2006 to 2018 were estimated and the spatial-temporal variation was analyzed. The results showed that: (1) The land use efficiency levels were quite different, and low-efficiency cities impacted the overall development process. (2) The efficiency values of construction land generally fluctuated and rose, meaning that room remains for future efficiency improvements. Cultivated land generally showed a high utilization efficiency, but it fluctuated and decreased. (3) The construction land-use efficiency was highest in the midland region, especially in Laiwu city, followed by the eastern region and Qingdao city, and the western region. The spatial variation in cultivated land presented a trend of “high in the middle, low in the periphery,” centered on Jinan and Yantai city. (4) Pure technical efficiency was the main restriction driving inefficient utilization in the western region, while scale efficiency played that role in the east. Based on the findings, policy suggestions were proposed to improve the land-use efficiency in Shandong and promote urban sustainable development. Keywords: land use; efficiency level; super-SBM model; Shandong Province; construction land; cultivated land 1. -

Spatial and Temporal Variation of VIIRS Derived AOT
Spatial and temporal variation of the Visible Infrared Imaging Radiometer Suite (VIIRS) derived aerosol optical thickness over East China Fei Menga, b, Changyong Caoc, Xi Shaoa aDepartment of Astronomy, University of Maryland, College Park, MD, USA bDepartment of Civil Engineering, Shandong Jianzhu University, Jinan, PR China cNOAA/ NESDIS/STAR, College Park, MD, USA Abstract Results The spatial and temporal variations in regional aerosol optical thickness (AOT) were investigated over Annual and seasonal AOT variations for different cities Shandong province of China based upon one year’s Visible Infrared Imaging Radiometer Suite (VIIRS) Averaged over the measurements in 2013, the minimum (Min.), maximum (Max.), mean, standard deviation data. The regional forest background annual mean AOT was 0.467 with a standard deviation of 0.339, (Std.) and variance of AOT in 17 cities (Fig.1) are presented in Table 1. which was much higher than the background continental AOT level of 0.10. Higher AOT values for the In order to better understand the AOT values in different cities, percent days with AOT≤0.5, 1.0≥AOT>0.5 and study region were mainly found in the spring and summer, especially from May to August, while the AOT>1.0 respectively in each cities were calculated (Fig.2). (a) (b) (c) (d) lowest mean aerosol values were seen in November and December. Urban areas all have obviously higher mean AOT values than the rural areas resulting from intense anthropogenic sources. Given that the forest background AOT represents the natural background level, anthropogenic emissions and C secondary aerosol generation contribute approximately 0.352 to the aerosol loading in this region. -
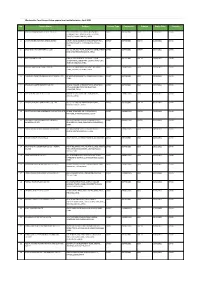
Apparel & Textile Factory List
Woolworths Food Group-Active apparel and textile factories- April 2021 No. Factory Name Address Factory Type Commodity Scheme Expiry Date Country 1 JIANGSU HONGMOFANG TEXTILE CO., LTD EAST CIFU ROAD, EAST RUISHENG AVENUE,, DIRECT SOFTGOODS BSCI 23/04/2021 CHINA ECONOMIC DEVELOPMENT ZONE, SHUYANG COUNTY,,SUQIAN,JIANGSU,,CHINA 2 LIANYUNGANG ZHAOWEN SHOES LIMITED 2 BEIHAI ROAD,ECONOMIC DEVELOPMENT AREA, DIRECT SOFTGOODS SMETA 11/05/2021 CHINA GUANNAN COUNTY,,LIANYUNGANG,JIANGSU,, CHINA 3 ZHUCHENG YIXIN GARMENT CO., LTD NO. 321 SHUNDU ROAD,,ECONOMIC DEVELOPMENT DIRECT SOFTGOODS SMETA 13/07/2021 CHINA ZONE,,ZHUCHENG,SHANDONG,,CHINA 4 HRX FASHION CO LTD 1000 METERS SOUTH OF GUOCANG TOWN DIRECT SOFTGOODS SMETA 25/08/2021 CHINA GOVERNMENT,,WENSHANG COUNTY, JINING CITY, JINING,SHANDONG,,CHINA 5 PUJIANG KINGSHOW CARPET CO LTD NO.75-1 ZHEN PU ROAD, PU JIANG, ZHE JIANG, DIRECT HARDGOODS BSCI 24/12/2021 CHINA CHINA,,PUJIANG,ZHEJIANG,,CHINA 6 YANGZHOU TENGYI SHOES MANUFACTURE CO., LTD. 13 WEST HONGCHENG RD,,,FANGXIANG,JIANGSU,, DIRECT SOFTGOODS BSCI 22/10/2021 CHINA CHINA 7 ZHAOYUAN CASTTE GARMENT CO LTD PANJIAJI VILLAGE, LINGLONG TOWN,,ZHAOYUAN DIRECT SOFTGOODS BSCI 06/07/2021 CHINA CITY, SHANDONG PROVINCE,ZHAOYUAN, SHANDONG,,CHINA 8 RUGAO HONGTAI TEXTILE CO LTD XINJIAN VILLAGE, JIANGAN TOWN,,RUGAO, DIRECT HARDGOODS BSCI 07/12/2021 CHINA JIANGSU,,CHINA 9 NANJING BIAOMEI HOMETEXTILES CO.,LTD NO.13 ERST WUCHU ROAD,HENGXI TOWN,,, DIRECT SOFTGOODS SMETA 04/11/2021 CHINA NANJING,JIANGSU,,CHINA 10 NANTONG YAOXING HOUSEWARE PRODUCTS CO.,LTD NO.999, TONGFUBEI RD., CHONGCHUAN, DIRECT HARDGOODS SMETA 24/09/2021 CHINA NANTONG,,NANTONG,JIANGSU,,CHINA 11 CHAOZHOU CHAOAN ZHENGYUN CERAMICS QIAO HU VILLAGE, CHAOAN, CHAOZHOU CITY, DIRECT HARDGOODS SMETA 19/05/2021 CHINA INDUSTRIAL CO LTD GUANGDONG, CHINA,,CHAOZHOU,GUANGDONG,, CHINA 12 YANTAI PACIFIC HOME FASHION FUSHAN MILL NO. -

Cereal Series/Protein Series Jiangxi Cowin Food Co., Ltd. Huangjindui
产品总称 委托方名称(英) 申请地址(英) Huangjindui Industrial Park, Shanggao County, Yichun City, Jiangxi Province, Cereal Series/Protein Series Jiangxi Cowin Food Co., Ltd. China Folic acid/D-calcium Pantothenate/Thiamine Mononitrate/Thiamine East of Huangdian Village (West of Tongxingfengan), Kenli Town, Kenli County, Hydrochloride/Riboflavin/Beta Alanine/Pyridoxine Xinfa Pharmaceutical Co., Ltd. Dongying City, Shandong Province, 257500, China Hydrochloride/Sucralose/Dexpanthenol LMZ Herbal Toothpaste Liuzhou LMZ Co.,Ltd. No.282 Donghuan Road,Liuzhou City,Guangxi,China Flavor/Seasoning Hubei Handyware Food Biotech Co.,Ltd. 6 Dongdi Road, Xiantao City, Hubei Province, China SODIUM CARBOXYMETHYL CELLULOSE(CMC) ANQIU EAGLE CELLULOSE CO., LTD Xinbingmaying Village, Linghe Town, Anqiu City, Weifang City, Shandong Province No. 569, Yingerle Road, Economic Development Zone, Qingyun County, Dezhou, biscuit Shandong Yingerle Hwa Tai Food Industry Co., Ltd Shandong, China (Mainland) Maltose, Malt Extract, Dry Malt Extract, Barley Extract Guangzhou Heliyuan Foodstuff Co.,LTD Mache Village, Shitan Town, Zengcheng, Guangzhou,Guangdong,China No.3, Xinxing Road, Wuqing Development Area, Tianjin Hi-tech Industrial Park, Non-Dairy Whip Topping\PREMIX Rich Bakery Products(Tianjin)Co.,Ltd. Tianjin, China. Edible oils and fats / Filling of foods/Milk Beverages TIANJIN YOSHIYOSHI FOOD CO., LTD. No. 52 Bohai Road, TEDA, Tianjin, China Solid beverage/Milk tea mate(Non dairy creamer)/Flavored 2nd phase of Diqiuhuanpo, Economic Development Zone, Deqing County, Huzhou Zhejiang Qiyiniao Biological Technology Co., Ltd. concentrated beverage/ Fruit jam/Bubble jam City, Zhejiang Province, P.R. China Solid beverage/Flavored concentrated beverage/Concentrated juice/ Hangzhou Jiahe Food Co.,Ltd No.5 Yaojia Road Gouzhuang Liangzhu Street Yuhang District Hangzhou Fruit Jam Production of Hydrolyzed Vegetable Protein Powder/Caramel Color/Red Fermented Rice Powder/Monascus Red Color/Monascus Yellow Shandong Zhonghui Biotechnology Co., Ltd. -

Slip Op. 19-67 UNITED STATES COURT OF
Case 1:18-cv-00002-JCG Document 81 Filed 06/03/19 Page 1 of 30 Slip Op. 19-67 UNITED STATES COURT OF INTERNATIONAL TRADE LINYI CHENGEN IMPORT AND EXPORT CO., LTD., Plaintiff, and CELTIC CO., LTD. ET AL., Consolidated Plaintiffs, Before: Jennifer Choe-Groves, Judge v. Consol. Court No. 18-00002 UNITED STATES, Defendant, and COALITION FOR FAIR TRADE IN HARDWOOD PLYWOOD, Defendant-Intervenor. OPINION AND ORDER [Sustaining in part and remanding in part the U.S. Department of Commerce’s final determination in the antidumping duty investigation of certain hardwood plywood products from the People’s Republic of China.] Dated: June 3, 2019 Gregory S. Menegaz and Alexandra H. Salzman, deKieffer & Horgan, PLLC, of Washington, D.C., argued for Plaintiff Linyi Chengen Import and Export Co., Ltd., Consolidated Plaintiffs Celtic Co., Ltd., Jiaxing Gsun Import & Export Co., Ltd., Suqian Hopeway International Trade Co., Ltd., Anhui Hoda Wood Co., Ltd., Shanghai Futuwood Trading Co., Ltd., Linyi Evergreen Wood Co., Ltd., Xuzhou Jiangyang Wood Industries Co., Ltd., Xuzhou Timber International Trade Co. Ltd., Linyi Sanfortune Wood Co., Ltd., Linyi Mingzhu Wood Co., Ltd., Xuzhou Andefu Wood Co., Ltd., Suining Pengxiang Wood Co., Ltd., Xuzhou Shengping Import and Export Co., Ltd., Xuzhou Pinlin International Trade Co. Ltd., Linyi Glary Plywood Co., Ltd., Case 1:18-cv-00002-JCG Document 81 Filed 06/03/19 Page 2 of 30 Consol. Court No. 18-00002 Page 2 Linyi Linhai Wood Co., Ltd., Linyi Hengsheng Wood Industry Co., Ltd., Shandong Qishan International Trading