DOCSLIB.ORG

A Really Friendly Guide to Wavelets

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Really Friendly Guide to Wavelets A Really Friendly Guide to Wavelets © C. Valens, 1999 [email protected] A Really Friendly Guide to Wavelets – © C. Valens, 1999 – [email protected] Disclaimer This tutorial is aimed at the engineer, not the mathematician. This does not mean that there will be no mathematics, it just means that there will be no proofs in the text. In my humble opinion, mathematical papers are completely unreadable because of the proofs that clutter the text. For proofs the reader is pointed to suitable references. The equations presented are there to illustrate and to clarify things, I hope. It should not be necessary to understand all the equations in order to understand the theory. However, to understand this tutorial, a mathematical background on an engineering level is required. Also some knowledge of signal processing theory might come in handy. The information presented in this tutorial is believed to be correct. However, no responsibilty whatsoever will be accepted for any damage whatsoever due to errors or misleading statements or whatsoever in this tutorial. Should there be anything incorrect, incomplete or not clear in this text, please let me know so that I can improve this tutorial. 2 A Really Friendly Guide to Wavelets – © C. Valens, 1999 – [email protected] Table of Contents 1. Introduction 2. The continuous wavelet transform 3. Wavelet properties 4. Discrete wavelets 5. A band-pass filter 6. Intermezzo: a constraint 7. The scaling function 8. Subband coding 9. The discrete wavelet transform 10. Coda 11. References 3 A Really Friendly Guide to Wavelets – © C. Valens, 1999 – [email protected] 1. Introduction It is well known from Fourier theory that a signal can be expressed as the sum of a, possibly infinite, series of sines and cosines. This sum is also referred to as a Fourier expansion. The big disadvantage of a Fourier expansion however is that it has only frequency resolution and no time resolution. This means that although we might be able to determine all the frequencies present in a signal, we do not know when they are present. To overcome this problem in the past decades several solutions have been developed which are more or less able to represent a signal in the time and frequency domain at the same time. The idea behind these time-frequency joint representations is to cut the signal of interest into several parts and then analyze the parts separately. It is clear that analyzing a signal this way will give more information about the when and where of different frequency components, but it leads to a fundamental problem as well: how to cut the signal? Suppose that we want to know exactly all the frequency components present at a certain moment in time. We cut out only this very short time window using a Dirac pulse1, transform it to the frequency domain and … something is very wrong. The problem here is that cutting the signal corresponds to a convolution between the signal and the cutting window. Since convolution in the time domain is identical to multiplication in the frequency domain and since the Fourier transform of a Dirac pulse contains all possible frequencies the frequency components of the signal will be smeared out all over the frequency axis. In fact this situation is the opposite of the standard Fourier transform since we now have time resolution but no frequency resolution whatsoever. The underlying principle of the phenomena just described is Heisenberg’s uncertainty principle, which, in signal processing terms, states that it is impossible to know the exact frequency and the exact time of occurrence of this frequency in a signal. In other words, a signal can simply not be represented as a point in the time-frequency space. The uncertainty principle shows that it is very important how one cuts the signal. The wavelet transform or wavelet analysis is probably the most recent solution to overcome the shortcomings of the Fourier transform. In wavelet analysis the use of a fully scalable modulated window solves the signal-cutting problem. The window is shifted along the signal and for every position the spectrum is calculated. Then this process is repeated many times with a slightly shorter (or longer) window for every new cycle. In the end the result will be a collection of time-frequency representations of the signal, all with different resolutions. Because of this collection of representations we can speak of a multiresolution analysis. In the case of wavelets we normally do not speak about time-frequency representations but about time-scale representations, scale being in a way the opposite of frequency, because the term frequency is reserved for the Fourier transform. Since from literature it is not always clear what is meant by small and large scales, I will define it here as follows: the large scale is the big picture, while the small scales show the details. Thus, going from large scale to small scale is in this context equal to zooming in. 1 A Dirac pulse is defined as f(t) = 1 at t = 0 and f(t) = 0 for all other t. 4 A Really Friendly Guide to Wavelets – © C. Valens, 1999 – [email protected] In the following sections I will present the wavelet transform and develop a scheme that will allow us to implement the wavelet transform in an efficient way on a digital computer. The transform will be so efficient that it does not even use wavelets anymore. (The careful reader might raise an eyebrow here and ask: “Surely you can’t be serious?”2) But before we continue a disclaimer. Since wavelet theory is not a new thing anymore, it has been around now for fifteen years, say, I will not present a full and in-depth theory here. Several good textbooks on wavelet theory are available and many readable papers with a good review of wavelet theory have been published. The list of references at the end of this report contains pointers to texts with more extensive wavelet theory coverage like (in random order) [Kai94], [Wei94], [She96], [Bur98], [Dau92], [Hub96], [Mal89], [Vet92]. I do however present some mathematical background in order to tell a coherent and clear tale (I hope). Having this said, let’s go on to the wavelets. 2. The continuous wavelet transform The wavelet analysis described in the introduction is known as the continuous wavelet transform or CWT. More formally it is written as: γ τ = ψ* (s, ) ∫ f (t) s,τ (t)dt , (1) where * denotes complex conjugation. This equation shows how a function ƒ(t) is decomposed into a set of basis functions 5s,-(t), called the wavelets. The variables s and - are the new dimensions, scale and translation, after the wavelet transform. For completeness sake equation (2) gives the inverse wavelet transform. I will not expand on this since we are not going to use it: = γ τ ψ τ f (t) ∫∫ (s, ) s,τ (t)d ds .(2) The wavelets are generated from a single basic wavelet 5(t), the so-called mother wavelet, by scaling and translation: − τ ψ = 1 ψ t s,τ (t) .(3) s s In (3) s is the scale factor, - is the translation factor and the factor s-1/2 is for energy normalization across the different scales. It is important to note that in (1), (2) and (3) the wavelet basis functions are not specified. This is a difference between the wavelet transform and the Fourier transform, or other transforms. The theory of wavelet transforms 2 “I am serious, and don’t call me Shirley.” Leslie Nielsen as Dr. Rumack in the film Airplane! (1980). 5 A Really Friendly Guide to Wavelets – © C. Valens, 1999 – [email protected] deals with the general properties of the wavelets and wavelet transforms only. It defines a framework within one can design wavelets to taste and wishes. 3. Wavelet properties The most important properties of wavelets are the admissibility and the regularity conditions and these are the properties which gave wavelets their name. It can be shown [She96] that square integrable functions 5(t) satisfying the admissibility condition, | Ψ(ω) |2 ∫ dω < +∞ ,(4) | ω | can be used to first analyze and then reconstruct a signal without loss of information. In (4) 4(7) stands for the Fourier transform of 5(t). The admissibility condition implies that the Fourier transform of 5(t) vanishes at the zero frequency, i.e. | Ψ(ω) |2 = 0 .(5) ω=0 This means that wavelets must have a band-pass like spectrum. This is a very important observation, which we will use later on to build an efficient wavelet transform. A zero at the zero frequency also means that the average value of the wavelet in the time domain must be zero, ∫ ψ(t)dt = 0 ,(6) and therefore it must be oscillatory. In other words, 5(t) must be a wave. As can be seen from (1) the wavelet transform of a one-dimensional function is two-dimensional; the wavelet transform of a two-dimensional function is four-dimensional. The time-bandwidth product of the wavelet transform is the square of the input signal and for most practical applications this is not a desirable property. Therefore one imposes some additional conditions on the wavelet functions in order to make the wavelet transform decrease quickly with decreasing scale s. These are the regularity conditions and they state that the wavelet function should have some smoothness and concentration in both time and frequency domains. Regularity is a quite complex concept and we will try to explain it a little using the concept of vanishing moments.
Load more

Recommended publications
  • Scale Space Multiresolution Analysis of Random Signals
    Scale Space Multiresolution Analysis of Random Signals Lasse Holmstr¨om∗, Leena Pasanen Department of Mathematical Sciences, University of Oulu, Finland Reinhard Furrer Institute of Mathematics, University of Zurich,¨ Switzerland Stephan R. Sain National Center for Atmospheric Research, Boulder, Colorado, USA Abstract A method to capture the scale-dependent features in a random signal is pro- posed with the main focus on images and spatial fields defined on a regular grid. A technique based on scale space smoothing is used. However, where the usual scale space analysis approach is to suppress detail by increasing smoothing progressively, the proposed method instead considers differences of smooths at neighboring scales. A random signal can then be represented as a sum of such differences, a kind of a multiresolution analysis, each difference representing de- tails relevant at a particular scale or resolution. Bayesian analysis is used to infer which details are credible and which are just artifacts of random variation. The applicability of the method is demonstrated using noisy digital images as well as global temperature change fields produced by numerical climate prediction models. Keywords: Scale space smoothing, Bayesian methods, Image analysis, Climate research 1. Introduction In signal processing, smoothing is often used to suppress noise. An optimal level of smoothing is then of interest. In scale space analysis of noisy curves and images, instead of a single, in some sense “optimal” level of smoothing, a whole family of smooths is considered and each smooth is thought to provide information about the underlying object at a particular scale or resolution. The ∗Corresponding author ∗∗P.O.Box 3000, 90014 University of Oulu, Finland Tel.
    [Show full text]
  • Image Denoising Using Non Linear Diffusion Tensors
    2011 8th International Multi-Conference on Systems, Signals & Devices IMAGE DENOISING USING NON LINEAR DIFFUSION TENSORS Benzarti Faouzi, Hamid Amiri Signal, Image Processing and Pattern Recognition: TSIRF (ENIT) Email: [email protected] , [email protected] ABSTRACT linear models. Many approaches have been proposed to remove the noise effectively while preserving the original Image denoising is an important pre-processing step for image details and features as much as possible. In the past many image analysis and computer vision system. It few years, the use of non linear PDEs methods involving refers to the task of recovering a good estimate of the true anisotropic diffusion has significantly grown and image from a degraded observation without altering and becomes an important tool in contemporary image changing useful structure in the image such as processing. The key idea behind the anisotropic diffusion discontinuities and edges. In this paper, we propose a new is to incorporate an adaptative smoothness constraint in approach for image denoising based on the combination the denoising process. That is, the smooth is encouraged of two non linear diffusion tensors. One allows diffusion in a homogeneous region and discourage across along the orientation of greatest coherences, while the boundaries, in order to preserve the natural edge of the other allows diffusion along orthogonal directions. The image. One of the most successful tools for image idea is to track perfectly the local geometry of the denoising is the Total Variation (TV) model [9] [8][10] degraded image and applying anisotropic diffusion and the anisotropic smoothing model [1] which has since mainly along the preferred structure direction.
    [Show full text]
  • Scale-Space Theory for Multiscale Geometric Image Analysis
    Tutorial Scale-Space Theory for Multiscale Geometric Image Analysis Bart M. ter Haar Romeny, PhD Utrecht University, the Netherlands [email protected] Introduction Multiscale image analysis has gained firm ground in computer vision, image processing and models of biological vision. The approaches however have been characterised by a wide variety of techniques, many of them chosen ad hoc. Scale-space theory, as a relatively new field, has been established as a well founded, general and promising multiresolution technique for image structure analysis, both for 2D, 3D and time series. The rather mathematical nature of many of the classical papers in this field has prevented wide acceptance so far. This tutorial will try to bridge that gap by giving a comprehensible and intuitive introduction to this field. We also try, as a mutual inspiration, to relate the computer vision modeling to biological vision modeling. The mathematical rigor is much relaxed for the purpose of giving the broad picture. In appendix A a number of references are given as a good starting point for further reading. The multiscale nature of things In mathematics objects have no scale. We are familiar with the notion of points, that really shrink to zero, lines with zero width. In mathematics are no metrical units involved, as in physics. Neighborhoods, like necessary in the definition of differential operators, are defined as taken into the limit to zero, so we can really speak of local operators. In physics objects live on a range of scales. We need an instrument to do an observation (our eye, a camera) and it is the range that this instrument can see that we call the scale range.
    [Show full text]
  • An Overview of Wavelet Transform Concepts and Applications
    An overview of wavelet transform concepts and applications Christopher Liner, University of Houston February 26, 2010 Abstract The continuous wavelet transform utilizing a complex Morlet analyzing wavelet has a close connection to the Fourier transform and is a powerful analysis tool for decomposing broadband wavefield data. A wide range of seismic wavelet applications have been reported over the last three decades, and the free Seismic Unix processing system now contains a code (succwt) based on the work reported here. Introduction The continuous wavelet transform (CWT) is one method of investigating the time-frequency details of data whose spectral content varies with time (non-stationary time series). Moti- vation for the CWT can be found in Goupillaud et al. [12], along with a discussion of its relationship to the Fourier and Gabor transforms. As a brief overview, we note that French geophysicist J. Morlet worked with non- stationary time series in the late 1970's to find an alternative to the short-time Fourier transform (STFT). The STFT was known to have poor localization in both time and fre- quency, although it was a first step beyond the standard Fourier transform in the analysis of such data. Morlet's original wavelet transform idea was developed in collaboration with the- oretical physicist A. Grossmann, whose contributions included an exact inversion formula. A series of fundamental papers flowed from this collaboration [16, 12, 13], and connections were soon recognized between Morlet's wavelet transform and earlier methods, including harmonic analysis, scale-space representations, and conjugated quadrature filters. For fur- ther details, the interested reader is referred to Daubechies' [7] account of the early history of the wavelet transform.
    [Show full text]
  • A Low Bit Rate Audio Codec Using Wavelet Transform
    Navpreet Singh, Mandeep Kaur,Rajveer Kaur / International Journal of Engineering Research and Applications (IJERA) ISSN: 2248-9622 www.ijera.com Vol. 3, Issue 4, Jul-Aug 2013, pp.2222-2228 An Enhanced Low Bit Rate Audio Codec Using Discrete Wavelet Transform Navpreet Singh1, Mandeep Kaur2, Rajveer Kaur3 1,2(M. tech Students, Department of ECE, Guru kashi University, Talwandi Sabo(BTI.), Punjab, INDIA 3(Asst. Prof. Department of ECE, Guru Kashi University, Talwandi Sabo (BTI.), Punjab,INDIA Abstract Audio coding is the technology to represent information and perceptually irrelevant signal audio in digital form with as few bits as possible components can be separated and later removed. This while maintaining the intelligibility and quality class includes techniques such as subband coding; required for particular application. Interest in audio transform coding, critical band analysis, and masking coding is motivated by the evolution to digital effects. The second class takes advantage of the communications and the requirement to minimize statistical redundancy in audio signal and applies bit rate, and hence conserve bandwidth. There is some form of digital encoding. Examples of this class always a tradeoff between lowering the bit rate and include entropy coding in lossless compression and maintaining the delivered audio quality and scalar/vector quantization in lossy compression [1]. intelligibility. The wavelet transform has proven to Digital audio compression allows the be a valuable tool in many application areas for efficient storage and transmission of audio data. The analysis of nonstationary signals such as image and various audio compression techniques offer different audio signals. In this paper a low bit rate audio levels of complexity, compressed audio quality, and codec algorithm using wavelet transform has been amount of data compression.
    [Show full text]
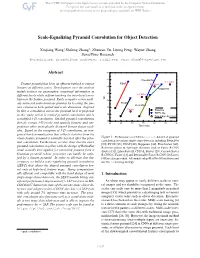
  • Scale-Equalizing Pyramid Convolution for Object Detection
    Scale-Equalizing Pyramid Convolution for Object Detection Xinjiang Wang,* Shilong Zhang∗, Zhuoran Yu, Litong Feng, Wayne Zhang SenseTime Research {wangxinjiang, zhangshilong, yuzhuoran, fenglitong, wayne.zhang}@sensetime.com Abstract 42 41 FreeAnchor C-Faster Feature pyramid has been an efficient method to extract FSAF D-Faster 40 features at different scales. Development over this method Reppoints mainly focuses on aggregating contextual information at 39 different levels while seldom touching the inter-level corre- L-Faster AP lation in the feature pyramid. Early computer vision meth- 38 ods extracted scale-invariant features by locating the fea- FCOS RetinaNet ture extrema in both spatial and scale dimension. Inspired 37 by this, a convolution across the pyramid level is proposed Faster Baseline 36 SEPC-lite in this study, which is termed pyramid convolution and is Two-stage detectors a modified 3-D convolution. Stacked pyramid convolutions 35 directly extract 3-D (scale and spatial) features and out- 60 65 70 75 80 85 90 performs other meticulously designed feature fusion mod- Time (ms) ules. Based on the viewpoint of 3-D convolution, an inte- grated batch normalization that collects statistics from the whole feature pyramid is naturally inserted after the pyra- Figure 1: Performance on COCO-minival dataset of pyramid mid convolution. Furthermore, we also show that the naive convolution in various single-stage detectors including RetinaNet [20], FCOS [38], FSAF [48], Reppoints [44], FreeAnchor [46]. pyramid convolution, together with the design of RetinaNet Reference points of two-stage detectors such as Faster R-CNN head, actually best applies for extracting features from a (Faster) [31], Libra Faster R-CNN (L-Faster) [29], Cascade Faster Gaussian pyramid, whose properties can hardly be satis- R-CNN (C-Faster) [1] and Deformable Faster R-CNN (D-Faster) fied by a feature pyramid.
    [Show full text]
  • Image Compression Techniques by Using Wavelet Transform
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by International Institute for Science, Technology and Education (IISTE): E-Journals Journal of Information Engineering and Applications www.iiste.org ISSN 2224-5782 (print) ISSN 2225-0506 (online) Vol 2, No.5, 2012 Image Compression Techniques by using Wavelet Transform V. V. Sunil Kumar 1* M. Indra Sena Reddy 2 1. Dept. of CSE, PBR Visvodaya Institute of Tech & Science, Kavali, Nellore (Dt), AP, INDIA 2. School of Computer science & Enginering, RGM College of Engineering & Tech. Nandyal, A.P, India * E-mail of the corresponding author: [email protected] Abstract This paper is concerned with a certain type of compression techniques by using wavelet transforms. Wavelets are used to characterize a complex pattern as a series of simple patterns and coefficients that, when multiplied and summed, reproduce the original pattern. The data compression schemes can be divided into lossless and lossy compression. Lossy compression generally provides much higher compression than lossless compression. Wavelets are a class of functions used to localize a given signal in both space and scaling domains. A MinImage was originally created to test one type of wavelet and the additional functionality was added to Image to support other wavelet types, and the EZW coding algorithm was implemented to achieve better compression. Keywords: Wavelet Transforms, Image Compression, Lossless Compression, Lossy Compression 1. Introduction Digital images are widely used in computer applications. Uncompressed digital images require considerable storage capacity and transmission bandwidth. Efficient image compression solutions are becoming more critical with the recent growth of data intensive, multimedia based web applications.
    [Show full text]
  • JPEG2000: Wavelets in Image Compression
    EE678 WAVELETS APPLICATION ASSIGNMENT 1 JPEG2000: Wavelets In Image Compression Group Members: Qutubuddin Saifee [email protected] 01d07009 Ankur Gupta [email protected] 01d070013 Nishant Singh [email protected] 01d07019 Abstract During the past decade, with the birth of wavelet theory and multiresolution analysis, image processing techniques based on wavelet transform have been extensively studied and tremendously improved. JPEG 2000 uses wavelet transform and provides an integrated toolbox to better address increasing needs for compression. In this report, we study the basic concepts of JPEG2000, the LeGall 5/3 and Daubechies 9/7 wavelets used in it and finally Embedded zerotree wavelet coding and Set Partitioning in Hierarchical Trees. Index Terms Wavelets, JPEG2000, Image Compression, LeGall, Daubechies, EZW, SPIHT. I. INTRODUCTION I NCE the mid 1980s, members from both the International Telecommunications Union (ITU) and the International SOrganization for Standardization (ISO) have been working together to establish a joint international standard for the compression of grayscale and color still images. This effort has been known as JPEG, the Joint Photographic Experts Group. The process was such that, after evaluating a number of coding schemes, the JPEG members selected a discrete cosine transform( DCT)-based method in 1988. From 1988 to 1990, the JPEG group continued its work by simulating, testing and documenting the algorithm. JPEG became Draft International Standard (DIS) in 1991 and International Standard (IS) in 1992. With the continual expansion of multimedia and Internet applications, the needs and requirements of the technologies used grew and evolved. In March 1997, a new call for contributions was launched for the development of a new standard for the compression of still images, the JPEG2000 standard.
    [Show full text]
  • Scale Normalized Image Pyramids with Autofocus for Object Detection
    1 Scale Normalized Image Pyramids with AutoFocus for Object Detection Bharat Singh, Mahyar Najibi, Abhishek Sharma and Larry S. Davis Abstract—We present an efficient foveal framework to perform object detection. A scale normalized image pyramid (SNIP) is generated that, like human vision, only attends to objects within a fixed size range at different scales. Such a restriction of objects’ size during training affords better learning of object-sensitive filters, and therefore, results in better accuracy. However, the use of an image pyramid increases the computational cost. Hence, we propose an efficient spatial sub-sampling scheme which only operates on fixed-size sub-regions likely to contain objects (as object locations are known during training). The resulting approach, referred to as Scale Normalized Image Pyramid with Efficient Resampling or SNIPER, yields up to 3× speed-up during training. Unfortunately, as object locations are unknown during inference, the entire image pyramid still needs processing. To this end, we adopt a coarse-to-fine approach, and predict the locations and extent of object-like regions which will be processed in successive scales of the image pyramid. Intuitively, it’s akin to our active human-vision that first skims over the field-of-view to spot interesting regions for further processing and only recognizes objects at the right resolution. The resulting algorithm is referred to as AutoFocus and results in a 2.5-5× speed-up during inference when used with SNIP. Code: https://github.com/mahyarnajibi/SNIPER Index Terms—Object Detection, Image Pyramids , Foveal vision, Scale-Space Theory, Deep-Learning. F 1 INTRODUCTION BJECT-detection is one of the most popular and widely O researched problems in the computer vision community, owing to its application to a myriad of industrial systems, such as autonomous driving, robotics, surveillance, activity-detection, scene-understanding and/or large-scale multimedia analysis.
    [Show full text]
  • Multi-Scale Edge Detection and Image Segmentation
    MULTI-SCALE EDGE DETECTION AND IMAGE SEGMENTATION Baris Sumengen, B. S. Manjunath ECE Department, UC, Santa Barbara 93106, Santa Barbara, CA, USA email: {sumengen,manj}@ece.ucsb.edu web: vision.ece.ucsb.edu ABSTRACT In this paper, we propose a novel multi-scale edge detection and vector field design scheme. We show that using multi- scale techniques edge detection and segmentation quality on natural images can be improved significantly. Our ap- proach eliminates the need for explicit scale selection and edge tracking. Our method favors edges that exist at a wide range of scales and localize these edges at finer scales. This work is then extended to multi-scale image segmentation us- (a) (b) (c) (d) ing our anisotropic diffusion scheme. Figure 1: Localized and clean edges using multiple scales. a) 1. INTRODUCTION Original image. b) Edge strengths at spatial scale σ = 1, c) Most edge detection algorithms specify a spatial scale at using scales from σ = 1 to σ = 4. d) at σ = 4. Edges are not which the edges are detected. Typically, edge detectors uti- well localized at σ = 4. lize local operators and the effective area of these local oper- ators define this spatial scale. The spatial scale usually corre- sponds to the level of smoothing of the image, for example, scales and generating a synthesis of these edges. On the the variance of the Gaussian smoothing. At small scales cor- other hand, it is desirable that the multi-scale information responding to finer image details, edge detectors find inten- is integrated to the edge detection at an earlier stage and the sity jumps in small neighborhoods.
    [Show full text]
  • Comparison of Image Compressions: Analog Transformations P
    Proceedings Comparison of Image Compressions: Analog † Transformations P Jose Balsa P CITIC Research Center, Universidade da Coruña (University of A Coruña), 15071 A Coruña, Spain; [email protected] † Presented at the 3rd XoveTIC Conference, A Coruña, Spain, 8–9 October 2020. Published: 21 August 2020 Abstract: A comparison between the four most used transforms, the discrete Fourier transform (DFT), discrete cosine transform (DCT), the Walsh–Hadamard transform (WHT) and the Haar- wavelet transform (DWT), for the transmission of analog images, varying their compression and comparing their quality, is presented. Additionally, performance tests are done for different levels of white Gaussian additive noise. Keywords: analog image transformation; analog image compression; analog image quality 1. Introduction Digitized image coding systems employ reversible mathematical transformations. These transformations change values and function domains in order to rearrange information in a way that condenses information important to human vision [1]. In the new domain, it is possible to filter out relevant information and discard information that is irrelevant or of lesser importance for image quality [2]. Both digital and analog systems use the same transformations in source coding. Some examples of digital systems that employ these transformations are JPEG, M-JPEG, JPEG2000, MPEG- 1, 2, 3 and 4, DV and HDV, among others. Although digital systems after transformation and filtering make use of digital lossless compression techniques, such as Huffman. In this work, we aim to make a comparison of the most commonly used transformations in state- of-the-art image compression systems. Typically, the transformations used to compress analog images work either on the entire image or on regions of the image.
    [Show full text]
  • Computer Vision: Edge Detection
    Edge Detection Edge detection Convert a 2D image into a set of curves • Extracts salient features of the scene • More compact than pixels Origin of Edges surface normal discontinuity depth discontinuity surface color discontinuity illumination discontinuity Edges are caused by a variety of factors Edge detection How can you tell that a pixel is on an edge? Profiles of image intensity edges Edge detection 1. Detection of short linear edge segments (edgels) 2. Aggregation of edgels into extended edges (maybe parametric description) Edgel detection • Difference operators • Parametric-model matchers Edge is Where Change Occurs Change is measured by derivative in 1D Biggest change, derivative has maximum magnitude Or 2nd derivative is zero. Image gradient The gradient of an image: The gradient points in the direction of most rapid change in intensity The gradient direction is given by: • how does this relate to the direction of the edge? The edge strength is given by the gradient magnitude The discrete gradient How can we differentiate a digital image f[x,y]? • Option 1: reconstruct a continuous image, then take gradient • Option 2: take discrete derivative (finite difference) How would you implement this as a cross-correlation? The Sobel operator Better approximations of the derivatives exist • The Sobel operators below are very commonly used -1 0 1 1 2 1 -2 0 2 0 0 0 -1 0 1 -1 -2 -1 • The standard defn. of the Sobel operator omits the 1/8 term – doesn’t make a difference for edge detection – the 1/8 term is needed to get the right gradient
    [Show full text]