Statistical Study of Rainfall Control: the Dagum Distribution and Applicability to the Southwest of Spain
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
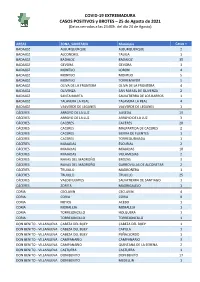
210825 Datos Covid- 19 EXT.Casos+ Y Brotes
COVID-19 EXTREMADURA CASOS POSITIVOS y BROTES – 25 de Agosto de 2021 (Datos cerrados a las 24:00h. del día 24 de Agosto) AREAS ZONA_SANITARIA Municipio Casos + BADAJOZ ALBURQUERQUE ALBURQUERQUE 2 BADAJOZ ALCONCHEL TALIGA 1 BADAJOZ BADAJOZ BADAJOZ 35 BADAJOZ GEVORA GEVORA 1 BADAJOZ MONTIJO LOBON 4 BADAJOZ MONTIJO MONTIJO 5 BADAJOZ MONTIJO TORREMAYOR 5 BADAJOZ OLIVA DE LA FRONTERA OLIVA DE LA FRONTERA 4 BADAJOZ OLIVENZA SAN RAFAEL DE OLIVENZA 2 BADAJOZ SANTA MARTA SALVATIERRA DE LOS BARROS 1 BADAJOZ TALAVERA LA REAL TALAVERA LA REAL 4 BADAJOZ VALVERDE DE LEGANES VALVERDE DE LEGANES 1 CÁCERES ARROYO DE LA LUZ ALISEDA 19 CÁCERES ARROYO DE LA LUZ ARROYO DE LA LUZ 3 CÁCERES CACERES CACERES 20 CÁCERES CACERES MALPARTIDA DE CACERES 2 CÁCERES CACERES SIERRA DE FUENTES 1 CÁCERES CACERES TORREQUEMADA 1 CÁCERES MIAJADAS ESCURIAL 2 CÁCERES MIAJADAS MIAJADAS 10 CÁCERES MIAJADAS VILLAMESIAS 2 CÁCERES NAVAS DEL MADROÑO BROZAS 3 CÁCERES NAVAS DEL MADROÑO GARROVILLAS DE ALCONETAR 2 CÁCERES TRUJILLO MADROÑERA 1 CÁCERES TRUJILLO TRUJILLO 25 CÁCERES VALDEFUENTES SALVATIERRA DE SANTIAGO 1 CÁCERES ZORITA MADRIGALEJO 1 CORIA CECLAVIN CECLAVIN 4 CORIA CORIA CORIA 9 CORIA HOYOS ACEBO 1 CORIA MORALEJA MORALEJA 1 CORIA TORREJONCILLO HOLGUERA 1 CORIA TORREJONCILLO TORREJONCILLO 1 DON BENITO - VILLANUEVA CABEZA DEL BUEY CABEZA DEL BUEY 1 DON BENITO - VILLANUEVA CABEZA DEL BUEY CAPILLA 1 DON BENITO - VILLANUEVA CABEZA DEL BUEY PEÑALSORDO 1 DON BENITO - VILLANUEVA CAMPANARIO CAMPANARIO 3 DON BENITO - VILLANUEVA CAMPANARIO QUINTANA DE LA SERENA 2 DON BENITO - VILLANUEVA CASTUERA CASTUERA 1 DON BENITO - VILLANUEVA DON BENITO DON BENITO 17 DON BENITO - VILLANUEVA DON BENITO MEDELLIN 1 COVID-19 EXTREMADURA CASOS POSITIVOS y BROTES – 25 de Agosto de 2021 (Datos cerrados a las 24:00h. -

\\P6\Comun\COMUN\MB3 PROYECTOS\Proyectos 2017
PLAN GENERAL MUNICIPAL DE PUEBLA DE ALCOCER OCTUBRE 2017 PLAN GENERAL MUNICIPAL DE PUEBLA DE ALCOCER. DOCUMENTO INICIAL ESTRATÉGICO. EQUIPO REDACTOR RAFAEL MESA HURTADO MB3-GESTIÓN. Técnicos Adscritos en el Equipo Redactor: Rafael Mesa Hurtado (Arquitecto, Máster en Urbanismo y Ordenación del Territorio) Francisco José Morcillo Balboa (MBA Administración Dirección de Empresas, Máster de Urbanismo y Ordenación del Territorio, Arquitecto Técnico, Estudios de Grado en Ingeniería de la Edificación) María Vélez Asins (Arquitecto) Berta Caldera Montalvo (Ingeniero Civil.) PLAN GENERAL MUNICIPAL DE PUEBLA DE ALCOCER DOCUMENTO INICIAL ESTRATÉGICO OCTUBRE 2017 INDICE 1. ANTECEDENTES ..................................................................................................................... 3 2. ALCANCE Y CONTENIDO DEL PGM PROPUESTO Y DE SUS ALTERNATIVAS, RAZONABLES, TÉCNICAS Y AMBIENTALES VIABLES. ................................................................ 3 2.1. ALCANCE Y CONTENIDO DEL PGM PROPUESTO. ....................................................... 3 2.2. ALTERNATIVAS RAZONABLES, TÉCNICAS Y AMBIENTALES VIABLES. ...................... 6 3. DIAGNÓSTICO PREVIO DE LA ZONA, TENIENDO EN CUENTA ASPECTOS ECONÓMICOS, SOCIALES Y AMBIENTALES. .............................................................................. 8 3.1. ENCUADRE TERRITORIAL .............................................................................................. 8 3.1.1. Encuadre Geográfico. ................................................................................................. -

Calendario Laboral 2021.Qxp M 23/11/20 17:33 Página 1
Calendario Laboral 2021.qxp_M 23/11/20 17:33 Página 1 JUNTA DE EXTREMADURA CALENDARIO LABORAL OFICIAL DE FIESTAS PARA LA Consejería de Educación y Empleo Dirección General de Trabajo COMUNIDAD AUTÓNOMA DE EXTREMADURA AÑO 2021 Y CUADRO HORARIO FIESTAS NACIONALES Y REGIONALES (Decreto 48/2020, de 26 de agosto; D.O.E. nº 170, de 1 de septiembre de 2020) EMPRESA Día 1 de enero: AÑO NUEVO Día 8 de septiembre: DÍA DE EXTREMADURA LOCALIDAD Día 6 de enero: EPIFANÍA DEL SEÑOR Día 12 de octubre: FIESTA NACIONAL DE ESPAÑA Día 19 de marzo: SAN JOSÉ Día 1 de noviembre: TODOS LOS SANTOS ACTIVIDAD N.º TRABAJADORES Día 1 de abril: JUEVES SANTO Día 6 de diciembre: DÍA DE LA CONSTITUCIÓN Día 2 de abril: VIERNES SANTO ESPAÑOLA N.º C.C. DE SEGURIDAD SOCIAL Día 1 de mayo: FIESTA DEL TRABAJO Día 8 de diciembre: INMACULADA CONCEPCIÓN Día 15 de agosto: ASUNCIÓN DE LA VIRGEN Día 25 de diciembre: NATIVIDAD DEL SEÑOR HORARIO DE TRABAJO ENERO FEBRERO MARZO INVIERNO VERANO LMXJVSD LMXJVSD LMXJVSD Desde: Hasta: Desde: Hasta: 1 2 3 1234567 1234567 456 78910 8 9 10 11 12 13 14 8 9 10 11 12 13 14 LUNES A VIERNES: LUNES A VIERNES: 11 12 13 14 15 16 17 15 16 17 18 19 20 21 15 16 17 18 19 20 21 Mañana: a Mañana: a 18 19 20 21 22 23 24 22 23 24 25 26 27 28 22 23 24 25 26 27 28 25 26 27 28 29 30 31 29 30 31 Tarde: a Tarde: a ABRIL MAYO JUNIO SÁBADO: a SÁBADO: a LMXJVSD LMXJVSD LMXJVSD DESCANSO: DESCANSO: 123 4 12 123456 567891011 3456789 7 8 9 10 11 12 13 12 13 14 15 16 17 18 10 11 12 13 14 15 16 14 15 16 17 18 19 20 EMPRESAS A TURNOS 19 20 21 22 23 24 25 17 18 19 20 21 22 23 21 22 23 24 25 26 27 24 26 27 28 29 30 31 25 26 27 28 29 30 28 29 30 1º JULIO AGOSTO SEPTIEMBRE 2º LMXJVSD LMXJVSD LMXJVSD 3º 1234 1 12345 567891011 2345678 678 9101112 , a de de 2021. -

Municipios En Situación De Prealerta
MUNICIPIOS EN SITUACIÓN DE PREALERTA Código de Denominación de la Unidad de Nombre de Unidad de Demanda Origen de recurso UTE Demanda Demanda A29B MANCOMUNIDAD DE MUNICIPIOS DE VEGAS ALTAS Abertura E. Zújar E09 A29B MANCOMUNIDAD DE MUNICIPIOS DE VEGAS ALTAS Acedera E. Zújar E09 E. Quejigo Gordo/E. La A8B MANCOMUNIDAD DE RIOFRIO Agudo E09 Colada A41B MANCOMUNIDAD DE LLERENA Ahillones E. Llerena/E. Los Molinos E12 E. Quejigo Gordo/E. La A21B ALAMILLO Alamillo E09 Colada A29B MANCOMUNIDAD DE MUNICIPIOS DE VEGAS ALTAS Alcollarín E. Zújar E09 A62B MANCOMUNIDAD DE AGUAS DEL ALCARRACHE Alconchel E. El Aguijón E18 A49B ALCONERA Alconera E. Los Molinos E12 A9B ALÍA Alía E. Alía E09 E. Quejigo Gordo/E. La A20B ALMADÉN Y COMARCA Almadén E09 Colada E. Quejigo Gordo/E. La A20B ALMADÉN Y COMARCA Almadenejos E09 Colada A51B MANCOMUNIDAD DE AGUAS EMBALSE DE JAIME OZORES Y FERIAAlmendralejo Río Guadiana V E09 A29B MANCOMUNIDAD DE MUNICIPIOS DE VEGAS ALTAS Almoharín E. Zújar E09 A7B ANCHURAS Anchuras Río Estenilla E09 A1B MANCOMUNIDAD DE VALDEHORNOS Arroba de los Montes Río Valdehornos E09 A65B ATALAYA Atalaya Pozo fuera de masa E12 A41B MANCOMUNIDAD DE LLERENA Azuaga E. Llerena/E. Los Molinos E12 A55B MANCOMUNIDAD DE MONTIJO Y COMARCA (LÁCARA SUR) Barbaño E. Canchales E14 A62B MANCOMUNIDAD DE AGUAS DEL ALCARRACHE Barcarrota E. El Aguijón E18 A16B6 MANCOMUNIDAD DE MUNICIPIOS "SIBERIA I" Baterno Río Esteras E09 Benquerencia de la A29B MANCOMUNIDAD DE MUNICIPIOS DE LA SERENA E. Zújar E09 Serena A41B MANCOMUNIDAD DE LLERENA Berlanga E. Llerena/E. Los Molinos E12 A27B BLÁZQUEZ (LOS) Blázquez (Los) Los Pedroches E11 A67B BURGUILLOS DEL CERRO Burguillos del Cerro E. -

Cdv De Badajoz
LIBRO OFICIAL DE REGISTRO DE CENTROS DE DESINFECCION DE VEHICULOS DE BADAJOZ Nº DE DATOS TELEFONO REGISTRO TITULAR 06/50/65/CDV MAFRESA 924 700 325 Ctra Fregenal- Sevilla, km 2. 06340 Fregenal de la Sierra 06/16/66/CDV CDV PUBLICO 924 736 026 Centro de manejo, ctra Salvaleón. 06160 Barcarrota 06/83/67/CDV A.D.S. EMERITA AUGUSTA 924 300 339 P.I. "El Prado", C/ Huesca, 9. 06800 Mérida 06/23/68/CDV S.C.L. ALANSER 924 601 032 Ctra Vva de la Serena a Andujar, km 66. 06600 Cabeza del buey 06/36/69/CDV MATADERO HERRUZO SANCHEZ, S.L. 924 761 515 Matadero frigorifico "La Serena". 06420 Castuera 06/6/70/CDV CDV PUBLICO 924 400 368 P.I. "San Blas", s/n. 06510 Alburquerque 06/158/71/CDV PIENSOS DARUZ, S.L. 924 563 222 Ctra Zafra- Los Santos, s/n. P.I. "Los Caños". 06300 Zafra 06/59/73/CDV CDV PUBLICO 924 895 585 Mercado de ganado. 06910 Granja de Torrehermosa 06/162/74/CDV CDV PUBLICO 924 366 001 Ctra EX105, KM 35,980 margen izdo. 06830 La Zarza 06/95/76/CDV S.A.T. "VILLA VIEJA" 924 494 129 Ctra Olivenza- Cheles, km 4,300. 06100 Olivenza Nº DE DATOS TELEFONO REGISTRO TITULAR 06/70/78/CDV CAMPOJEREZ 924 750 134 Ctra N- 435, km 74,600. 06380 Jerez de los Caballeros 06/74/79/CDV JAMON Y SALUD, S.A. 924 873 837 Ctra N- 432, km 112. 06900 Llerena 06/52/81/CDV OCCIDENTAL DE PIENSOS, S.A. -

Lavado De Contenedores
CALENDARIO JUNIO 2018 Lavado de contenedores Lunes Martes Miércoles Jueves Viernes Sábado Domingo 1 2 3 Alburquerque Esparragalejo Torremayor Torremejía Rena Villar de Rena Palazuelos Garlotos El Risco Sancti-Spíritu Valencia del Ventoso Valverde de Burguillos 4 5 6 7 8 9 10 Entrín Bajo La Albuera San Vicente de Calamonte La Codosera La Garrovilla Alcántara Calamonte Guadajira Alconchel Barcarrota Villanueva del Fresno Talavera la Real Talavera la Real Higuera de Vargas Medellín Valencia del Mombuey Campanario Orellana la Vieja Villagonzalo Mengabril Gargáligas Campillo de Llerena Malcocinado Puebla del Zaucejo Yelbes Torviscal Jerez de los Caballeros Valverde de Llerena Retamal de Llerena Granaja de Zurbarán Oliva de la Frontera Jerez de los Caballeros Jerez de los Caballeros Torrehermosa Casas de Don Pedro Zafra Zafra Esparragosa de Lares La Parra Hornachos Salvatierra de los Zafra Barros Zafra 11 12 13 14 15 16 17 Montijo Salvaleón Hernán Cortés Puebla de Obando Ruecas La Roca de la Sierra Carmonita Torrefresneda Cristina Cordobilla de Lácara Puebla de la Calzada Pueblonuevo Puebla de Alcocer Manchita La Nava de Santiago Fregenal de la Sierra Fregenal de la Sierra Feria Valdetorres Talarrubias La Morera Talarrubias Puerto Peña-Camping Nogales Ribera del Fresno Medina de las Torres Puebla de Sancho Pérez 18 19 20 21 22 23 24 Cheles Valdelacalzada Táliga Montijo Villar del Rey Montijo Valle de Santa Ana Montijo Don Benito Entrerríos Montijo Valle de Matamoros Barbaño Baterno Valdivia Don Benito Zahínos Don Benito (amarillos) Garbayuela -

6.º Primaria Lista Espera PILEX 2019. Res. Extraordinaria
ANEXO I-B PROGRAMA DE INMERSIONES LINGÜÍSTICAS EN EXTREMADURA (PILEX) ALUMNADO LISTA DE ESPERA - RESOLUCIÓN EXTRAORDINARIA 6.º PRIMARIA ORDEN APELLIDO 1 APELLIDO 2 NOMBRE CENTRO LOCALIDAD 192 Tarro Domínguez India C.E.I.P. Ntra. Sra. De la Asunción Valverde del Fresno 193 Berrocal Palomino Daniel C.E.I.P. Extremadura Cáceres 194 Galera Rico Carolina C.E.I.P. Adolfo Díaz Ambrona Valdelacalzada 195 Carmona García Ana C.E.I.P. Ntra. Sra. Asunción Lobón 196 Gutiérrez Murillo Gloria COL. Santa Eulalia-Escolapias Mérida 197 Parrón Leal Pilar C.E.I.P. Ntra. Sra. De la Luz Arroyo de la Luz 198 Gaitán Palomo Ismael Antonio C.E.I.P. De Gabriel Gevora 199 Ocejo Nogales Laura C.E.I.P. Virgen de Guadalupe Quintana de la Serena 200 Felipe Domínguez Paula C.R.A. Quercus Aldeacentenera 201 Arcos Fernández Manuel C.E.I.P. Ntra. Sra. De Piedraescrita Campanario 202 Escribano Tena Candela C.E.I.P. Ntra. Sra. De Consolación Monterrubio de la Serena 203 Sánchez Pérez Pedro C.R.A. Ambroz Zarza de Granadilla 204 Rodríguez Muriel Manuel C.E.I.P. De Prácticas Cáceres 205 Alvarado Bastida Irene C.E.I.P. Lope de Vega Badajoz 206 Villanueva Corrales Lorenzo C.E.I.P. Ntra. Sra. De la Montaña Cáceres 207 García Salomón Claudia C.E.I.P. La Acequia Puebla de Argeme 208 Fernàndez Escassi Paula Guadalupe C.E.I.P. Adolfo Díaz Ambrona Valdelacalzada 209 Muñoz Aranda José Manuel COL. María Auxiliadora Mérida 210 Fonseca Villalobos Paola C.E.I.P. Eloy Vela Corbacho Valle de Santa Ana 211 Iglesias Rocha Inés C.E.I.P. -

Acta Del Pleno
- 1 - B O R R A D O R ACTA DE LA SESION ORDINARIA CELEBRADA POR LA CORPORACION MUNICIPAL EN PLENO, EL DÍA ------------ 28-septiembre-2005 --------- En la Villa de Guareña, siendo las SEÑORES ASISTENTES: 20,30 horas del día veintiocho de septiembre de dos mil cinco, se Alcalde- Presidente: reúnen en el Salón de Actos de la Casa D. Rafael S. Carballo López Consistorial los señores Concejales que al margen se expresan, con objeto de Concejales: celebrar sesión ORDINARIA del Pleno D. Juan Carlos Romero Habas de este Ayuntamiento correspondiente D. Francisco Heras Moreno al mes de SEPTIEMBRE de 2005, para Dª Antonia Quirós García la que fueron convocados en forma D. Francisco J. Cerrato Isidoro legal. Dª Josefa Humánez Bravo D. Diego Gutiérrez Rigote D. Miguel Angel Durán Cerrato Preside el acto el señor Alcalde- D. Fernando L. Pérez de Lemus Presidente don Rafael-S. Carballo D. Antonio Barrero Mancha López, da fé del acto, el Secretario de D. Angel Gómez Pérez la Corporación, Dª. Mª Teresa Román D. Jesús Espino Morcillo García. D. Leopoldo Cortés Merino. Concejales que han Declarada abierta la sesión por la excusado asistencia: presidencia, son presentados a la consideración del Pleno los diferentes NINGUNO. asuntos que figuran en el “orden del día”, según la convocatoria que ha sido cursada a los señores Concejales con la antelación preceptiva, y adoptándose, en consecuencia, los acuerdos o resoluciones que seguidamente se especifican: 1º. LECTURA Y APROBACIÓN, SI PROCEDE, DE BORRADORES DEL ACTA DE LA SESION ANTERIOR. Se somete a la consideración del Pleno el borrador del acta de la sesión anterior, correspondientes al Pleno ordinario de 21 de Julio de 2005 y el Peno Ordinario 28-09-05. -

Ayuntamiento De Jerez De Los Caballeros Ayuntamiento
6070 31 Julio 1997 D.O.E.—Número 89 14.–Modelo de Proposición: dinaria de fecha 30-06-97, las Normas Subsidiarias de Planea- miento de Maguilla, redactadas por el Arquitecto D. Francisco D. ............................................................................, con domicilio en Barbudo Gironza, se someten a información pública por plazo de ........................................., Municipio ..................................., C.P. ......... un mes contado a partir de la publicación del presente anuncio y D.N.I. n.º ................., expedido en ................. con fecha .............., en el Diario Oficial de Extremadura o en el Boletín Oficial de la en nombre propio (o en representación de ........................ como Provincia de Badajoz si fuere de fecha posterior, durante el cual acredito por .......................) enterado de la convocatoria de subas- la documentación integrante de las mismas podrá ser examinada ta por procedimiento abierto, anunciada en el Boletín Oficial de la en el Ayuntamiento, en horario de oficinas, para formular las Provincia n.º ............. de fecha ............, tomo parte en la convoca- alegaciones y observaciones que se estimen oportunas. toria comprometiéndome a realizar las obras de Ejecución Reforma Zona Centro, en el precio de ................................. (letra y número) Al mismo tiempo queda suspendido el otorgamiento de licencias IVA incluido, con arreglo al proyecto técnico y Pliego de Cláusulas en el ambito territorial objeto del nuevo planeamiento por un Administrativas que acepto incondicionada e íntegramente, sin sal- plazo máximo de dos años, en los supuestos en que la actua- vedad alguna, haciendo constar que mantengo la oferta durante el ción pretendida contradiga una de las dos ordenaciones coexis- plazo de 1 año y no estoy incurso en ninguna de las circunstan- tentes. cias establecidas en el art. -

Calendario De Competiciones Fedexcaza – 2019
CALENDARIO DE COMPETICIONES FEDEXCAZA – 2019 COMPETICIÓN FECHA LUGAR DE CELEBRACIÓN PERDIZ CON RECLAMO CAMPEONATO DE EXTREMADURA 9 de Febrero Navalvillar de Pela CAMPEONATO DE ESPAÑA 23 Febrero Nalvalvillar de Pela CETRERÍA CAMPEONATO DE EXTREMADURA DE CETRERÍA (ALTANERÍA Y BAJO VUELO) 19 y 20 Enero Llerena SAN HUBERTO y PERROS DE MUESTRA CAMP. EXTREMADURA DE SAN HUBERTO 1ª Prueba puntuable 9 de Marzo Cabeza del Buey CAMP. EXTREMADURA DE SAN HUBERTO 2ª Prueba puntuable 23 de Marzo Calzadilla de los Barros CAMP. EXTREMADURA DE SAN HUBERTO 3ª Prueba puntuable 27 de Abril Campanario COPA DE EXTREMADURA DE SAN HUBERTO Mayo C.I Las Reinas PODENCOS* CAMPEONATO DE EXTREMADURA DE CAZA PRÁCTICA. (Abierto) 30 de Marzo Merida CAMPEONATO DE EXTREMADURA EN RECINTO CERRADO Por determinar Por determinar COMPAK SPORTING CTO. DE EXTREMADURA DE COMPAK SPORTING. 1ª Prueba Puntuable 7 Abril Navalvillar de Pela CTO. DE EXTREMADURA DE COMPAK SPORTING. 2ª Prueba Puntuable 21 Abril Malpartida de Plasencia CTO. DE EXTREMADURA DE LA EXCMA. DIPUTACIÓN DE BADAJOZ. Fase final 25 Mayo Jerez de los Caballeros RECORRIDOS DE CAZA CTO. DE EXTREMADURA DE RRCC. 1ª Prueba Puntuable 2 Junio Valencia de Alcántara CTO. DE EXTREMADURA DE RRCC. 2ª Prueba Puntuable 9 Junio Orellana la vieja CTO. DE EXTREMADURA DE LA EXCMA. DIPUTACIÓN DE CÁCERES. Fase final 23 Junio Jaraíz de la Vera CAZA MENOR CON PERRO CAMPEONATO PROVINCIAL DE BADAJOZ 26 de Octubre Valdecaballeros CAMPEONATO PROVINCIAL DE CÁCERES 26 de Octubre Por determinar CAMPEONATO DE EXTREMADURA 10 de Noviembre Badajoz CAZA CON ARCO CAMP. AUT. TROFEO EXCMA. DIP. DE CÁCERES DE RR.CC CON ARCO 19 Mayo Plasencia BECADAS TROFEO EXCMA. -

En La Vecina Localidad De Ribera Del Fresno Aún Cuentan Que La Línea
PK 47: DIARIO DEL FERROCARRIL A SU PASO POR VILLAFRANCA PK 47: DIARIO DEL FERROCARRIL A SU PASO POR VILLAFRANCA JOSÉ LÓPEZ VÁZQUEZ Tec. Museo de Villafranca Cofundador de A-MUVI Foto: Pepe López "Seamos sinceros, si hoy hubiera que inventar el ferrocarril, nadie lo haría". (Frase pronunciada en un congreso internacional de ferrocarriles en los años 80) Ironía o verdad, contradicción o exageración, lo cierto es que la llegada del ferrocarril a Villafranca provocó en 1879 una transformación fundamental en la economía de la zona. En la vecina localidad de Ribera del Fresno aún cuentan que la línea férrea Mérida‐Los Rosales (SE) estaba destinada a trochar sus tierras, pero que por entonces la oligarquía “imperante” de la población se opuso por miedo a posibles incendios en sus pastos como consecuencia de las chispas que pudiese ocasionar la fricción del tren. Si esta negación fue real, personalmente, creo que se equivocaron al desistir de tan interesante proyecto de infraestructura y revolución en el transporte, siempre y cuando queramos ver la parte positiva. JOSÉ LÓPEZ VÁZQUEZ 46 EL HINOJAL Revista de estudios del MUVI Número 9 Verdaderamente creo más en un rumor, no es del todo cierto lo que hasta nuestros días se sigue divulgando entre vecinos de Ribera con el resto de poblaciones inmediatas cuando hablamos de comparaciones. Había otros muchos intereses también económicos, es evidente, pero la realidad es otra que iré detallando. En la actualidad, a unos 11 km del lugar mencionado, la estación de Villafranca de los Barros, nuestra ciudad, una estación (nº. 40005) con altitud de 412 metros, situada en el punto kilométrico 43,7 de la línea 516 de Adif que va de Mérida a Los Rosales, y entre la estación de Almendralejo y la estación de Los Santos de Maimona, comarca de Tierra de Barros en la provincia de Badajoz, Extremadura. -

Titular Poblacion Provincia Telefono Cul Descripcion A.G
TITULAR POBLACION PROVINCIA TELEFONO CUL_DESCRIPCION A.G. LOMAS DEL RIO ZUJAR S.L. CASTUERA BADAJOZ 635609601 ALMENDRO A.G. LOMAS DEL RIO ZUJAR S.L. CASTUERA BADAJOZ 635609601 VIÑA ABILIO GALLEGO SANCHEZ CABEZA DEL BUEY BADAJOZ 699553214 PASTOS ABILIO GALLEGO SANCHEZ CABEZA DEL BUEY BADAJOZ 699553214 TRANQUILLON ABILIO MANUEL BAUTISTA SANCHEZ ALMENDRALEJO BADAJOZ 924670609 CEBADA ABILIO MANUEL BAUTISTA SANCHEZ ALMENDRALEJO BADAJOZ 924670609 OLIVAR ACACIO HERNANDEZ GALAYO CABEZUELA DEL VALLE CACERES 636103481 CEREZO ACACIO HERNANDEZ GALAYO CABEZUELA DEL VALLE CACERES 636103481 CIRUELO ACACIO HERNANDEZ GALAYO CABEZUELA DEL VALLE CACERES 636103481 KIWI ACACIO HERNANDEZ GALAYO CABEZUELA DEL VALLE CACERES 636103481 MELOCOTONERO ACACIO HERNANDEZ GALAYO CABEZUELA DEL VALLE CACERES 636103481 NARANJO ACACIO HERNANDEZ GALAYO CABEZUELA DEL VALLE CACERES 636103481 NOGAL ADELA AMAGO AMAGO TALAVERA DE LA REINA TOLEDO 925822594 PASTOS ADELA HIERRO DELGADO CORDOBILLA DE LÁCARA BADAJOZ 618314540 OLIVAR ADELA MOLINA BOLA CORDOBILLA DE LÁCARA BADAJOZ 924320285 OLIVAR ADELA PINILLA GALLARIN VILLAFRANCA DE LOS BARROS BADAJOZ 666663249 OLIVAR ADELA PINILLA GALLARIN VILLAFRANCA DE LOS BARROS BADAJOZ 666663249 VIÑA ADELA VILLALBA AMAGO MONESTERIO BADAJOZ 639290676 PASTOS ADELAIDA BOLA CHANCLON CORDOBILLA DE LÁCARA BADAJOZ 924320109 OLIVAR ADELAIDA GONZALEZ GORDO CEREZO CACERES 927673687 OLIVAR ADELAIDA HIERRO LLAGAS CÁCERES CACERES 924224984 OLIVAR ADOLFO MEGIAS PEREZ ALCONERA BADAJOZ 924570078 OLIVAR ADORACION BASTIAS NOGALES ESPARRAGOSA DE LA SERENA BADAJOZ