Validating the Test-Field Method with Mean-Field Dynamo Simulations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Author Accepted Manuscript
University of Dundee Introduction Brandenburg, A.; Candelaresi, S.; Gent, F. A. Published in: Geophysical and Astrophysical Fluid Dynamics DOI: 10.1080/03091929.2019.1677015 Publication date: 2020 Document Version Peer reviewed version Link to publication in Discovery Research Portal Citation for published version (APA): Brandenburg, A., Candelaresi, S., & Gent, F. A. (2020). Introduction. Geophysical and Astrophysical Fluid Dynamics, 114(1-2), 1-7. https://doi.org/10.1080/03091929.2019.1677015 General rights Copyright and moral rights for the publications made accessible in Discovery Research Portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from Discovery Research Portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain. • You may freely distribute the URL identifying the publication in the public portal. Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Download date: 02. Oct. 2021 February 26, 2020 Geophysical and Astrophysical Fluid Dynamics paper GEOPHYSICAL & ASTROPHYSICAL FLUID DYNAMICS 1 Introduction to The Physics and Algorithms of the Pencil Code A. Brandenburg Nordita, KTH Royal Institute of Technology and Stockholm University, Stockholm, Sweden http://orcid.org/0000-0002-7304-021X S. Candelaresi Division of Mathematics, University of Dundee, Dundee, UK now at School of Mathematics & Statistics, University of Glasgow, Glasgow, UK http://orcid.org/0000-0002-7666-8504 F. -

Stellar X-Rays and Magnetic Activity in 3D MHD Coronal Models J
A&A 652, A32 (2021) Astronomy https://doi.org/10.1051/0004-6361/202040192 & © J. Zhuleku et al. 2021 Astrophysics Stellar X-rays and magnetic activity in 3D MHD coronal models J. Zhuleku, J. Warnecke, and H. Peter Max Planck Institute for Solar System Research, 37077 Göttingen, Germany e-mail: [email protected] Received 21 December 2020 / Accepted 28 May 2021 ABSTRACT Context. Observations suggest a power-law relation between the coronal emission in X-rays, LX, and the total (unsigned) magnetic flux at the stellar surface, Φ. The physics basis for this relation is poorly understood. Aims. We use three-dimensional (3D) magnetohydrodynamics (MHD) numerical models of the coronae above active regions, that is, strong concentrations of magnetic field, to investigate the LX versus Φ relation and illustrate this relation with an analytical model based on simple well-established scaling relations. Methods. In the 3D MHD model horizontal (convective) motions near the surface induce currents in the coronal magnetic field that are dissipated and heat the plasma. This self-consistently creates a corona with a temperature of 1 MK. We run a series of models that differ in terms of the (unsigned) magnetic flux at the surface by changing the (peak) magnetic field strength while keeping all other parameters fixed. Results. In the 3D MHD models we find that the energy input into the corona, characterized by either the Poynting flux or the total volumetric heating, scales roughly quadratically with the unsigned surface flux Φ. This is expected from heating through field-line 3:44 braiding. Our central result is the nonlinear scaling of the X-ray emission as LX Φ . -

The Pencil Code, a Modular MPI Code for Partial Differential Equations And
The Pencil Code, a modular MPI code for partial differential equations and particles: multipurpose and multiuser-maintained The Pencil Code Collaboration1, Axel Brandenburg1, 2, 3, Anders Johansen4, Philippe A. Bourdin5, Wolfgang Dobler6, Wladimir Lyra7, Matthias Rheinhardt8, Sven Bingert9, Nils Erland L. Haugen10, 11, 1, Antony Mee12, Frederick Gent8, 13, Natalia Babkovskaia14, Chao-Chin Yang15, Tobias Heinemann16, Boris Dintrans17, Dhrubaditya Mitra1, Simon Candelaresi18, Jörn Warnecke19, Petri J. Käpylä20, Andreas Schreiber14, Piyali Chatterjee21, Maarit J. Käpylä8, 19, Xiang-Yu Li1, Jonas Krüger10, 11, Jørgen R. Aarnes11, Graeme R. Sarson13, Jeffrey S. Oishi22, Jennifer Schober23, Raphaël Plasson24, Christer Sandin1, Ewa Karchniwy11, 25, Luiz Felippe S. Rodrigues13, 26, Alexander Hubbard27, Gustavo Guerrero28, Andrew Snodin13, Illa R. Losada1, Johannes Pekkilä8, and Chengeng Qian29 1 Nordita, KTH Royal Institute of Technology and Stockholm University, Sweden 2 Department of Astronomy, Stockholm University, Sweden 3 McWilliams Center for Cosmology & Department of Physics, Carnegie Mellon University, PA, USA 4 GLOBE Institute, University of Copenhagen, Denmark 5 Space Research Institute, Graz, Austria 6 Bruker, Potsdam, Germany 7 New Mexico State University, Department of Astronomy, Las Cruces, NM, USA 8 Astroinformatics, Department of Computer Science, Aalto University, Finland 9 Gesellschaft für wissenschaftliche Datenverarbeitung mbH Göttingen, Germany 10 SINTEF Energy Research, Trondheim, Norway 11 Norwegian University of Science -

A Task Scheduler for Astaroth, the Astrophysics Simulation Framework
A Task Scheduler for Astaroth, the Astrophysics Simulation Framework Oskar Lappi 37146 MSc, Eng. Computer Engineering Instructors: Johannes Pekkilä Supervisor: Jan Westerholm Maarit Käpylä Faculty of Science and Engineering Astroinformatics group Åbo Akademi University Aalto University 2021 Abstract Computational scientists use numerical simulations performed by computers to create new knowledge about complex systems. To give an example, computational astrophysi- cists run large magnetohydrodynamics simulations to study the evolution of magnetic fields in stars [1]. Simulation workloads are growing in size as scientists are interested in studying sys- tems of increasingly large scales and high resolutions. As a consequence, performance requirements for the underlying computing platforms are becoming tougher. To meet these requirements, many high-performance computer clusters use GPUs to- gether with high-speed networks to accelerate computation. The fluid dynamics library Astaroth is built for such GPU clusters and has demonstrated a 10x speedup when com- pared to the equivalent CPU-based Pencil Code library still used by computational physi- cists today [2]. This thesis has been done in coordination with the research team that created Astaroth and builds on their findings. My goal has been to create a new version of Astaroth that performs better at distributed scale. Earlier versions of Astaroth perform well due to optimized compute kernels and a coarse pipeline that overlaps computation and communication. The work done for this thesis consists of a finer-grained dependency analysis and a task graph scheduler that exploits the analysis to schedule tasks dynamically. The task scheduler improves the performance of Astaroth for realistic bandwidth- bound workloads by up to 25% and improves the overall scalability of Astaroth. -
![Arxiv:1806.01570V3 [Astro-Ph.GA] 18 Jun 2019](https://docslib.b-cdn.net/cover/1960/arxiv-1806-01570v3-astro-ph-ga-18-jun-2019-9861960.webp)
Arxiv:1806.01570V3 [Astro-Ph.GA] 18 Jun 2019
June 19, 2019 Geophysical and Astrophysical Fluid Dynamics GGAF-2018-0035-Gent Geophysical and Astrophysical Fluid Dynamics Vol. 00, No. 00, 00 Month 2018, 1{25 Modelling supernova driven turbulence F. A. Genta;d∗, M-M. Mac Lowb, M. J. K¨apyl¨ac;a, G. R. Sarsond and J. F. Hollinsd a ReSoLVE Centre of Excellence, Dept. Computer Science, Aalto University, FI-00076, Aalto, Finland b Dept. of Astrophysics, American Museum of Natural History, New York, NY 10024-5192, USA Center for Computational Astrophysics, Flatiron Institute, New York, NY 10010, USA cMax Planck Institute for Solar System Research, D-37707, G¨ottingen,Germany dSchool of Mathematics, Statistics and Physics, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK (submitted May 2018) High Mach number shocks are ubiquitous in interstellar turbulence. The Pencil Code is particularly well suited to the study of magnetohydrodynamics in weakly compressible turbulence and the numerical in- vestigation of dynamos because of its high-order advection and time evolution algorithms. However, the high-order algorithms and lack of Riemann solver to follow shocks make it less well suited to handling high Mach number shocks, such as those produced by supernovae (SNe). Here, we outline methods required to enable the code to efficiently and accurately model SNe, using parameters that allow stable simulation of SN-driven turbulence, in order to construct a physically realistic galactic dynamo model. These include the resolution of shocks with artificial viscosity, thermal conductivity, and mass diffusion; the correction of the mass diffusion terms; and a novel generalization of the Courant condition to include all source terms in the momentum and energy equations. -
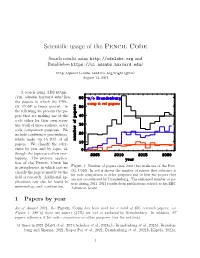
Scientific Usage of the Pencil Code
Scientific usage of the Pencil Code Search results using http://adslabs.org and Bumblebee https://ui.adsabs.harvard.edu/ http://pencil-code.nordita.org/highlights/ August 14, 2021 A search using ADS https: //ui.adsabs.harvard.edu/ lists the papers in which the Pen- cil Code is being quoted. In the following we present the pa- pers that are making use of the code either for their own scien- tific work of those authors, or for code comparison purposes. We include conference proceedings, which make up 15–20% of all papers. We classify the refer- ences by year and by topic, al- though the topics are often over- lapping. The primary applica- tion of the Pencil Code lies Pen- in astrophysics, in which case we Figure 1: Number of papers since 2003 that make use of the cil Code. In red is shown the number of papers that reference it classify the papers mostly by the for code comparison or other purposes and in blue the papers that field of research. Additional ap- are not co-authored by Brandenburg. The enhanced number of pa- plications can also be found in pers during 2011–2013 results from publications related to his ERC meteorology and combustion. Advanced Grant. 1 Papers by year As of August 2021, the Pencil Code has been used for a total of 605 research papers; see Figure 1; 286 of those are papers (47%) are not co-authored by Brandenburg. In addition, 97 papers reference it for code comparison or other purposes (see the red line). 41 times in 2021 (Maiti et al., 2021; Schober et al., 2021a,b; Brandenburg et al., 2021d; Branden- burg and Sharma,