Elementary Cellular Automata Along with Delay Sensitivity Can Model
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Urban Population Growth in the Municipalities of North 24 Parganas, It Is Clear That North 24 Parganas Has Retained a High Level of Urbanization Since Independence
World Wide Journal of Multidisciplinary Research and Development WWJMRD 2018; 4(3): 68-73 www.wwjmrd.com International Journal Peer Reviewed Journal Urban Population Growth in the Municipalities of Refereed Journal Indexed Journal North 24 Parganas: A Spatio-Temporal Analysis UGC Approved Journal Impact Factor MJIF: 4.25 E-ISSN: 2454-6615 Mashihur Rahaman Mashihur Rahaman Abstract Research Scholar The rapid growth of urban population causes various problems in urban centres like increased P.G. Department of unemployment, economic instability, lacks of urban facilities, unhygienic environmental conditions Geography, Utkal University, Vani Vihar, Bhubaneswar, etc. People were well aware about the importance of population studies from very beginning. Odisha, India Explosively growing of urban population has attracted the attention of urban geographers and town planners. For country like India, it is very important to study the decadal variation of population growth, it helps in realizing problems. The population growth and socio-economic changes are closely related to each other. In present study North 24 Parana’s has been chosen as study area. The level of urbanization remained high in the district (57.6 % in 2011). Rapid increase in urbanization can be attributed to growth of Kolkata metropolis.Barasat is now within greater Kolkata (Kolkata 124).From 1991 onwards the real estate business in this district thrived and projects were taken which are more of residential type than business type. The aim of the present paper is to investigate the change in urban population growth rate of municipality wise during the three decades 1981-91, 1991- 2001 and 2001-2011. Due to push-pull factors the rural-urban migration is causing the process of urbanization. -
24 Parganas North
Draft Electoral Roll of North 24 Pgs. Region of The West Bengal State Cooperative Bank Ltd. as on 08/06/2016 Name of the Address of the Name of Father's Membership 51. No. Address Society Society Representative Name 51 No 1 20 ViII & PO Kankpul Late ViII & PO Kankpul, Kankpul SKUS Amrita Kumar Dist 24 Pgs (North) Shachindra Dist 24 Pgs (North) Ltd Gupta PIN 743 272 Nath Gupta Pin-743272 2 680 ViII & PO Shimulia Simulia ViII & PO Simulia PS Gopalnagar Dist Late Sunil Nischintapur Subrata Banerjee PS Gopalnagar Dist 24 Pgs (North) PIN Banerjee SKUS Ltd 24 Pgs(North) 743262 3 Viii &PO ViII Asa Bottala PO 82 Natagram SKUS Natagram PS Bibekananda Late Lalit Natagram PS Ltd Gaighata Dist 24 Majumder Majumder Gaighata Dist 24 Pgs (North) Pgs (North) 4 205 ViII & PO Ghosalati ViII & PO Goshalati Ghosalati SKUS Md Mofachhel Late Momin PS Hasnabad Dist PS Hasnabad Dist l.td Gazi Gazi 24 Pgs (North) 24 Pgs (North) 5 ViII Fulbari PO 193 ViII Gohalapara PO Nahata PS Late Fulbari SKUS Hingli PS Gopal Gopalnagar Dist Fakir Chand Dutta Nityananda Ltd Nagar Dist 24 Pgs 24 Pgs (North) PIN Dutta (North) 743290 6 164 Sankchura ViII & PO Soladana Late Subodh ViII Kathri PO Taki Bagundi SKUS PS Basirhat Dist 24 Biswanath Ghosh Chandra PS Basirhat Dist 24 Ltd Pgs (North) Ghosh Pgs (North) 7 Rasulpur PO 3/311 Rasulpur PO Bhanderkola Rasulpur SKUS Bhandarkola PS Late Sri bash Kalipada Sarkar Bongaon Dist 24 Ltd Gopalnagar Dist Sarkar Pgs (North) PIN 24 Pgs (North) 743701 8 Viii Kumuria PO 180 ViII & PO Hingli PS Late Gopal Hingli PS Kumuria SKUS Gopalnagar Dist Santi Pada Hazra Chandra Gopalnagar Dist 24 Ltd 24 Pgs (North) Hazra Pgs (North) PIN 743290 9 ViII Abad 240 ViII & PO Dakshin Kharampur PO Dakshin Bhebia Bhebia PS Karim Baksh Kharampur PS Daud Ali Sardar SKUS Ltd Hasnabad Dist 24 Sardar Hasnabad Dist 24 Pgs (North) Pgs (North) PIN 743456 t'-& GAUTAM KUMAR DATTA Assistant Returning Officer The West Bengal State Co-operative Bank Ltd. -

List of Municipalities Sl.No
LIST OF MUNICIPAL BODIES WHERE ELECTIONS WILL BE HELD IN THE MIDDLE OF 2010 SL.NO. DISTRICT NAME OF MUNICIPALITY 1 Cooch Behar Municipality 2 Tufanganj Municipality Cooch Behar 3 Dinhata Municipality 4 Mathabhanga Municipality 5 Jalpaiguri Jalpaiguri Municipality 6 English Bazar Municipality Malda 7 Old Malda Municipality 8 Murshidabad Municipality 9 Jiaganj-Azimganj Municipality 10 Kandi Municipality Murshidabad 11 Jangipur Municipality 12 Dhulian Municipality 13 Beldanga Municipality 14 Nabadwip Municipality 15 Santipur Municipality 16 Ranaghat Municipality 17Nadia Birnagar Municipality 18 Kalyani Municipality 19 Gayeshpur Municipality 20 Taherpur Municipality 21 Kanchrapara Municipality 22 Halishar Municipality 23 Naihati Municipality 24 Bhatpara Municipality 25North 24-Parganas Garulia Municipality 26 North Barrackkpore Municipality 27 Barrackpore Municipality 28 Titagarh Municipality 29 Khardah Municipality \\Mc-4\D\Munc. Elec-2010\LIST OF MUNICIPALITIES SL.NO. DISTRICT NAME OF MUNICIPALITY 30 Kamarhati Municipality 31 Baranagar Municipality 32 North Dum Dum Municipality 33 Bongaon Municipality 34 Gobardanga Municipality 35North 24-Parganas Barasat Municipality 36 Baduria Municipality 37 Basirhat Municipality 38 Taki Municipality 39 New Barrackpore Municipality 40 Ashokenagar-Kalyangarh Municipality 41 Bidhannagar Municipality 42 Budge Budge Municipality 43South 24-Parganas Baruipur Municipality 44 Jaynagar-Mazilpur Municipality 45 Howrah Bally Municipality 46 Hooghly-Chinsurah Municipality 47 Bansberia Municipality 48 Serampore Municipality 49 Baidyabati Municipality 50 Champadany Municipality 51 Bhadreswar Municipality Hooghly 52 Rishra Municipality 53 Konnagar Municipality 54 Arambagh Municipality 55 Uttarpara Kotrung Municipality 56 Tarakeswar Municipality 57 Chandernagar Municipal Corporation 58 Tamluk Municipality Purba Medinipur 59 Contai Municipality 60 Chandrakona Municipality 61 Ramjibanpur Municipality 62Paschim Medinipur Khirpai Municipality 63 Kharar Municipality 64 Khargapur Municipality 65 Ghatal Municipality \\Mc-4\D\Munc. -

Rainfall, North 24-Parganas
DISTRICT DISASTER MANAGEMENT PLAN 2016 - 17 NORTHNORTH 2424 PARGANASPARGANAS,, BARASATBARASAT MAP OF NORTH 24 PARGANAS DISTRICT DISASTER VULNERABILITY MAPS PUBLISHED BY GOVERNMENT OF INDIA SHOWING VULNERABILITY OF NORTH 24 PGS. DISTRICT TO NATURAL DISASTERS CONTENTS Sl. No. Subject Page No. 1. Foreword 2. Introduction & Objectives 3. District Profile 4. Disaster History of the District 5. Disaster vulnerability of the District 6. Why Disaster Management Plan 7. Control Room 8. Early Warnings 9. Rainfall 10. Communication Plan 11. Communication Plan at G.P. Level 12. Awareness 13. Mock Drill 14. Relief Godown 15. Flood Shelter 16. List of Flood Shelter 17. Cyclone Shelter (MPCS) 18. List of Helipad 19. List of Divers 20. List of Ambulance 21. List of Mechanized Boat 22. List of Saw Mill 23. Disaster Event-2015 24. Disaster Management Plan-Health Dept. 25. Disaster Management Plan-Food & Supply 26. Disaster Management Plan-ARD 27. Disaster Management Plan-Agriculture 28. Disaster Management Plan-Horticulture 29. Disaster Management Plan-PHE 30. Disaster Management Plan-Fisheries 31. Disaster Management Plan-Forest 32. Disaster Management Plan-W.B.S.E.D.C.L 33. Disaster Management Plan-Bidyadhari Drainage 34. Disaster Management Plan-Basirhat Irrigation FOREWORD The district, North 24-parganas, has been divided geographically into three parts, e.g. (a) vast reverine belt in the Southern part of Basirhat Sub-Divn. (Sundarban area), (b) the industrial belt of Barrackpore Sub-Division and (c) vast cultivating plain land in the Bongaon Sub-division and adjoining part of Barrackpore, Barasat & Northern part of Basirhat Sub-Divisions The drainage capabilities of the canals, rivers etc. -

BARASAT DMSION' PWD R^*O^. Rnoda Rovra Road
Public Works DePartment Government of West Bengal Notification No. 3p-37ll3l43l-R/pl- dated 11.08.2015.-ln exercise of the power conferred by Section 5 of the West as the said Act), the Governor is Bengal Highways Act, lg64 (west Ben. Act XXVIII of 1964) (hereinafter referred to of clause (d) of section 2 pleased hereby to appoint, with immediate effect, the Highway Authority within the meaning its length under under the Public of the said Act as mentioned in column (4) of Schedule below, in respect of road and (3), respectively, of the said works Department in North 24 parganas district as mentioned in column (2) and column Schedule, for the purposes of the said Act:- SCHEDULE NORTH 24 PARGANAS DISTRICT DMSION: BARASAT DMSION' PWD q0- Highway sl. Name of the Road oE Authority No. (4) I (3) 5.00 I Yol Road (0.00 40.00 2 ET Eloeirhqf I Road kmo to 40.00 km (40-00 6.40 .t Elooirhof I Rond kmn to 46.40 km pa\El 0.50 4 ith hnth side ). D.":"L"r ljosnqhed Rnad (0 00 kmn to 13.00 13.00 3.00 gasirhat Flasnabad Road (13.00 kmp to 16'00 kmp) t 18.00 7 R^*o^. Rnoda Rovra Road (0.00 kmp to 18.00 km 1 5.60 8 gonsron gugda Boyra Road (18.00 kmp to 33'60 km) 16.00 9 BonguonChakdah Ro@ l.60 0 Bonsaon Diagonal MuniciPal Road t.20 i) Executive I Bongaon Station Road Engineer, Barasat 2.07 2 Gachha to BOP Road Division r 0.00 13 C,qiohqlq Gnhnrdansn Road ii) Assistant 0.80 4 Hakimpur Bithari Road Engineers under 15.50 5 Hasnabad Hingalgani Road Barasat Division r.80 6 Hasnabad Takighat Road having t7.60 7 Helencha Sindhrani Duttafulia Road jurisdiction of the 33.60 8 Hinealeani Dulduli Hemnagar Road road. -

Details of Student 17-19
AL HERA COLLEGE OF EDUCATION (CODE-ERCAPP1485) Recognized by NCTE & Affiliated to WBUTTEPA Vill-Kodalia,P.O-Dakshin Bagundi,P.S-Basirhat,North 24 Parganas,West Bengal,Pin-743429 Student Details: Number of students course -wise; year -wise along with details: 2017 -19 Year of Admission Sl. Name Father’ s Address Category Year of Result Percent Contact Admission No. of the (Gen/SC/ Admission age No. / fee (Receipt student Name OBC/Others)ST/ mobile No., Date& admitte No. Amount) d 1 2 3 4 5 6 7 8 9 10 VIll -Taki P.O-Taki Ananya Dey P.S-Hasnabad 9501/30.06.17/ 1. Ananta Kr. Dey OBC-B 2017 8609417441 Dist- North 24 pgs Rs.30000.00 Pin-743429 West Bengal VIll-Patilachandra P.O-P.Madhyampur Mostafa Sardar P.S-Basirhat 9876/30.06.17/ 2. Chhurat Ali Sardar OBC-A 2017 8926716243 Dist- North 24 pgs Rs.20000.00 Pin-743429 West Bengal VIll-Patilachandra P.O-P.Madhyampur Rejaul Islam Gazi P.S-Basirhat 7101/30.06.17/ 3. Badel Gazi OBC-B 2017 8926720402 Dist- North 24 pgs Rs.40000.00 Pin- West Bengal VIll -Tokipur P.O-Tokipur Mallika Maity P.S-Hasnabad 7876/30.06.17/ 4. Asit Kr Maity GEN 2017 7602724442 Dist- North 24 pgs Rs.20000.00 Pin-743429 West Bengal VIll-Naihati P.O-Badartala Soumen Bandyopadhyay Late Gobinda P.S-Basirhat 7802/29.06.17/ 5. GEN 2017 9434686780 Bandyopadhyay Dist- North 24 pgs Rs.20000.00 Pin-743492 West Bengal VIll -Angnara P.O-South Kalibari Salma Khatun P.S-Hasnabad 8001/30.06.17/ 6. -

Barasat Dmsion. Pwd
Public Works Department Government of West Bengal Notification No.3P-37l13/411-R/PL dated 11.08.2015.- In exercise of the power conferred by section 3 of the West Bengal Highways Act, 1964 (West Ben. Act XXVIII of 1964) (hereinafter referred to as the said Act), the Governor is pleased hereby to declare, with immediate effect, the road and its length as mentioned in column (2) and column (3), respectively, of Schedule below under the Public Works Department in North 24 Parganas district, as highway within the meaning of clause ( c) of section 2 of the said Act:- SCHEDULE NORTH 24 PARGANAS DISTRICT DMSION: BARASAT DMSION. PWD sl. Name of the Road ao- No. OE (1) {?) (3) 1 Banipur Rastriya Kalyan Bhavan Road s.00 2 Barasat Basirhat I ndaghat Road (0.00 kmp to 40.00 kmp) 40.00 3 Barasat Basirhat I ndaghat Road (40.00 kmp to 46.40 km) 6.40 /'l Barasat ROB along with both side approaches 0.50 5 Basirhat Hasnabad Road (0.00 kmp to 13.00 kmp) r 3.00 6 Basirhat Hasnabad Road ( 13.00 kmp to I 6.00 kmp) 3.00 7 Bongaon Bagda Boyra Road (0.00 kmp to 18.00 kmp) 18.00 8 Bongaon Bagda Boyra Road (18.00 kmp to 33.60 km) 15.60 9 Bonsaon Chakdah Road (0.00 kmp to 16.00 kmp) r 6.00 0 Bongaon Diagonal Municipal Road 1.60 1 Bongaon Station Road 1.20 2 Gachha to BOP Road 2.07 a J Gaighata Gobordanga Road 10.00 4 Hakimpur Bithari Road 0.80 5 Hasnabad Hinealsani Road 15.50 6 Hasnabad Takishat Road r .80 7 Helencha Sindhrani Duttafulia Road 17.60 8 Hinealeani Dulduli Hemnasar Road 3 3.60 9 Khaspur Kheyaghat Road ( Old Tentulia Maslamdapur Road) r.80 20 Kholapaota Baduria Maslandapur Habra Road (0.00 kmp to 24.45 km) 24.45 21 Kholapaota Baduria Maslandapur Habra Road (24.45 km to 32.00 kmp) 7.55 22 Old Satkhira Road to ltindaehatBazar 0.50 Paikpara Sutia Road 8.60 24 Raiberia Bhurkunda Road 3.20 25 Road within Baduria Municipality 3.30 26 Sayestanagar Kaiiuri Chituri Road 17.10 27 Swarupnasar P.S Link Road 0.80 28 Tentulia Maslandapur Road 15.00 DMSION: BARRACKPUR DMSION, PWD aot sl. -

North Twenty Four Parganas.Pdf
Block Name GP Name Positive Cases AMDANGA ADHATA AMDANGA AMDANGA AMDANGA BERABERIA AMDANGA BODAI AMDANGA CHANDIGARH AMDANGA MARICHA AMDANGA SADHANPUR AMDANGA TARABERIA BAGDA ASHARU BAGDA BAGDA BAGDA BAYRA BAGDA HELENCHA BAGDA KONIARA-I BAGDA KONIARA-II BAGDA MALIPOTA BAGDA RANAGHAT BAGDA SINDRANI BARASAT-I CHHOTO JAGULIA BARASAT-I DATTAPUKUR-I BARASAT-I DATTAPUKUR-II BARASAT-I ICHHAPUR-NILGANJ BARASAT-I KADAMBAGACHHI BARASAT-I KASHIMPUR BARASAT-I KOTRA BARASAT-I PASCHIM KHILKAPUR BARASAT-I PURBA KHILKAPUR BARASAT-II CHANDIGARH-ROHANDA 2 BARASAT-II DADPUR BARASAT-II FALTI BELIAGHATA BARASAT-II KEMIA KAMAR PARA BARASAT-II KIRTIPUR-I BARASAT-II KIRTIPUR-II BARASAT-II SHASAN BARRACKPUR-I JETHIA BARRACKPUR-I KAMPA-CHAKLA BARRACKPUR-I KOWGACHI-I BARRACKPUR-I KOWGACHI-II BARRACKPUR-I MAJHIPARA-PALASI BARRACKPUR-I MAMUDPUR BARRACKPUR-I PANPUR-KEUTIA BARRACKPUR-I SHIBDASPUR BARRACKPUR-II BANDIPUR BARRACKPUR-II BILKANDA-I BARRACKPUR-II BILKANDA-II 1 BARRACKPUR-II MOHANPUR 3 BARRACKPUR-II PATULIA 1 Block Name GP Name Positive Cases BARRACKPUR-II SEWLI BONGAON AKAIPUR 1 BONGAON BAIRAMPUR 1 BONGAON CHAWBERIA-I BONGAON CHAWBERIA-II BONGAON CHHAIGHORIA BONGAON DHARAM PUKURIA BONGAON DIGHARI BONGAON GANGANANDAPUR BONGAON GANGRAPOTA BONGAON GHATBOUR BONGAON GOPALNAGAR-I BONGAON GOPALNAGAR-II 1 BONGAON KALUPUR BONGAON PALLA BONGAON SUNDARPUR BONGAON TENGRA DEGANGA AMULIA DEGANGA BERACHAMPA-I DEGANGA BERACHAMPA-II DEGANGA CHAKLA DEGANGA CHAMPATALA DEGANGA CHAURASI DEGANGA DEGANGA-I DEGANGA DEGANGA-II DEGANGA HADIPUR JHIKRA-I DEGANGA HADIPUR JHIKRA-II DEGANGA -

COVID Session Sites North 24 Parganas 10.3.21
COVID Session Sites North 24 Parganas 10.3.21 Sl No District /Block/ ULB/ Hospital Session Site name Address Functional Status Ashoknagar Kalyangarh 1 Ashoknagar SGH Govt. Functional Municipality 2 Bangaon Municipality Bongaon SDH & SSH Govt. Functional 3 Baranagar Municipality Baranagar SGH Govt. Functional 4 Barasat Municipality Barasat DH Govt. Functional 5 Barrackpur - I Barrackpore SDH Govt. Functional 6 Bhatpara Municipality Bhatpara SGH Govt. Functional Bidhannagar Municipal 7 Salt Lake SDH Govt. Functional Corporation 8 Habra Municipality Habra SGH Govt. Functional 9 Kamarhati Municipality Session 1 Academic Building Govt. Functional Session 2 Academic Building, Sagar Dutta Medical college 10 Kamarhati Municipality Govt. Functional and hospital 11 Kamarhati Municipality Session 3 Lecture Theater Govt. Functional 12 Kamarhati Municipality Session 4 Physiology Dept Govt. Functional 13 Kamarhati Municipality Session 5 Central Library Govt. Functional 14 Kamarhati Municipality Collage of Medicine & Sagore Dutta MCH Govt. Functional 15 Khardaha Municipality Balaram SGH Govt. Functional 16 Naihati Municipality Naihati SGH Govt. Functional 17 Panihati Municipality Panihati SGH Govt. Functional 18 Amdanga Amdanga RH Govt. Functional 19 Bagda Bagdah RH Govt. Functional 20 Barasat - I Chhotojagulia BPHC Govt. Functional 21 Barasat - II Madhyamgram RH Govt. Functional 22 Barrackpur - I Nanna RH Govt. Functional 23 Barrackpur - II Bandipur BPHC Govt. Functional 24 Bongaon Sundarpur BPHC Govt. Functional 25 Deganga Biswanathpur RH Govt. Functional 26 Gaighata Chandpara RH Govt. Functional 27 Habra - I Maslandpur RH Govt. Functional 28 Habra - II Sabdalpur RH Govt. Functional 29 Rajarhat Rekjoani RH Govt. Functional 30 Amdanga Adhata PHC Govt. Functional 31 Amdanga Beraberia PHC Govt. Functional 32 Amdanga Maricha PHC Govt. Functional 33 Bagda Koniara PHC Govt. -

HFW-27038/17/2019-NHM SEC-Dept.Of H&FW/3641
GOVERNMENT OF WEST BENGAL HEALTH & FAMILYWELFAREDEPARTMENT NATIONALHEALTHMISSION(NHM) GN-29, 2ndFLOOR,GRANTHAGARBHAWAN, SWASTHYABHAWANPREMISES,SECTOR-V - SALTLAKE,BIDHANNAGAR,KOLKATA- 700 091. NATIONAL URBAN HEALTH MISSION ~ 033 - 2333-0432, !Ali 033 - 2357 - 7930, e-Mail 10: [email protected]; website: www.wbhealth.gov.in Memo No. HFW-27038/17/2019-NHM SEC-Dept.of H&FW/ l_Glt1 Date: 11/11/2019 From : Additional Mission Director, NHM & Joint Secretary, Government of West Bengal To Chief Medical Officer of Health, (Howrah / North 24 Parganas / Basirhat HD) Sub: Meeting on Infrastructure strengthening works under NUHM Madam / Sir, A meeting will be held on 19th November, 2019 from 11.00 A.M.at Muktodhara, 5th Floor, Meeting Hall, Swasthya Sathi Building, Swasthya Bhawan, Kolkata - 700 091 to review the infrastructure strengthening works and utilisation offund under NUHMin different ULBsunder your district. Agenda of the review meeting are as follows- 1. Construction of new U-PHCbuildings 2. Procurement and installation of lab-equipments 3. Financial review The following officials of your district and ULBs as mentioned below may please be requested to make it convenient to attend the meeting. Level Participants 1. Consultant Epidemiologist, NUHM / District Programme Coordinator, NHM, DPMU (in absence of Consultant Epidemiologist, NUHM, District Programme Coordinator, NHMmay be allowed to participate) 2. Assistant Engineer / Sub-Assistant Engineer, NHM, DPMU (in absence of District Assistant Engineer, NHM, Sub-Assistant Engineer, NHM may be allowed to participate) 3. Accounts Manager, NUHM / District Accounts Manager, NHM, DPMU (in absence of Accounts Manager, NUHM,District Accounts Manager, NHM may be allowed to participate) 1. Nodal Officer, NUHM(Municipal Corporation / Municipality) 2. -
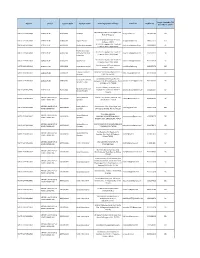
District Sector Course Code Course Name Training Center Address E-Mail ID Mobile No 31St March 2019
Target Available Till District Sector Course Code Course Name Training Center Address E-mail ID Mobile No 31st March 2019 Mama Bhagina Bus stand, Bagdah, Dist- NORTH 24 PARGANAS AGRICULTURE AGR/Q0801 Gardener [email protected] 9874062186 570 Norh 24 Parganas Prafulla Kanan, VIP Road, Kestopur, NORTH 24 PARGANAS AGRICULTURE AGR/Q1201 Organic Grower [email protected] 9830037376 254 Kolkata - 700101 Vill +PO+PS : Bagdah, Dist : North 24 NORTH 24 PARGANAS AGRICULTURE AGR/Q4303 Poultry farm manager [email protected] 9434102419 30 Parganas, State : West Bengal Poultry feed, food Vill +PO+PS : Bagdah, Dist : North 24 NORTH 24 PARGANAS AGRICULTURE AGR/Q4305 safety and labelling [email protected] 9434102419 30 Parganas, State : West Bengal supervisor Vill +PO+PS : Bagdah, Dist : North 24 NORTH 24 PARGANAS AGRICULTURE AGR/Q4501 Goat Farmer [email protected] 9434102419 30 Parganas, State : West Bengal Prafulla Kanan, VIP Road, Kestopur, NORTH 24 PARGANAS AGRICULTURE AGR/Q4904 Aqua culture worker [email protected] 9830037376 200 Kolkata - 700101 Fisheries Extension BARASAT, Stn. Rd, Near Platform no1, 7 NORTH 24 PARGANAS AGRICULTURE AGR/Q5107 [email protected] 9331040169 90 Associate K.N.C. Rd., Kol-124 Gurukul Edutech Duttapukur,Vill : Agriculture Extension NORTH 24 PARGANAS AGRICULTURE AGR/Q7601 Gangapur, P.O. & P.S. Duttapukur, North [email protected] 9051352337 30 Service Provider 24 Parganas Pin 743248 Gurukul Edutech, Haroa,Vill & P.O. Agriculture Extension NORTH 24 PARGANAS AGRICULTURE AGR/Q7601 Gopalpur,P.S. Haroa Dist. North 24 [email protected] 9051352337 60 Service Provider Parganas APPAREL, MADE-UPS & Sewing Machine Plot No - 3B, Block-LA, Sector-III, Salt NORTH 24 PARGANAS AMH/Q0301 [email protected] 9679669547 50 HOME FURNISHING Operator Lake, Kolkata - 700098 APPAREL, MADE-UPS & Sewing Machine Jhautalamore, Post. -
![Containment Zones in North 24 Pgs [ As on 06/05/2020 ] Without Positives](https://docslib.b-cdn.net/cover/5302/containment-zones-in-north-24-pgs-as-on-06-05-2020-without-positives-3205302.webp)
Containment Zones in North 24 Pgs [ As on 06/05/2020 ] Without Positives
Containment Zones in North 24 Pgs [ as on 06/05/2020 ] without positives SL Muni/Block Ward/GP Locality Police Station No N. N. Road, South Dumdum 1 23 Dum Dum Municipality 2 30 Lake Town Block A, Block B Kolkata 89 Lake Town 33(part) 3 34(part), Dakshindari road, Laketown. Lake Town 35 (part) 4 Gorakshabasi Road. Nagerbazar Dum Dum 25 5 Kajipara,Kabi Nabin Sen Rd Dum Dum South Dum Dum 6 21 Nayapati Road Dum Dum Diamond city, Jossore Road 7 27 Dum Dum 8 28 Dum Dum park Lake Town 9 29 Bangur, Laketown Lake Town 10 16 Roy Mallickpara Colony, Dum Dum Dum Dum Rastraguru Avenue, Ramghar 11 8 Dum Dum Colony,NAGAR BAZAR 12 26 Kabi Bharat Chandra Road Dum Dum 13 25 Jogendra Basak Road, Baranagar Baranagar 14 29 Nanda Kumar Road, Baranagar Baranagar 15 Baranagar 13 Gopal Lal Thakur Road, Baranagar Baranagar 16 17 Nabin Chandra Das Road Baranagar 17 4 Kumarpara Lane,Jhilbagan, Kol-35 Baranagar 18 17 Rathtala, Kamarhati Belghoria Club Town Heights, Belgharia, 19 16 Belghoria Rathtala Jaganta Pally, Deshapriya Nagar, 20 25 Belghoria Nandan Kanan, Belghoria 21 26 Rani Park, Belghoria Belghoria 22 Kamarhati 18 Sarat Pally, Belghoria Belghoria 23 1 Banerjee Bagan Kamarhati Belghoria OLD NIMTA RD, Thakurdas 24 21 Banerjee Road, KP Ghoshal Road, Belghoria Belghoria 25 13 Kumud Ghosal Rd., Ariadaha Belghoria 26 4 CHARU MARKET Belghoria 27 2 TOOTH BAGAN Belghoria Airport Gate No. 1,East kamalpur, 28 11 Dum Dum Dum Dum RBC Road, Dum Dum Central Jail 29 20 Dum Dum Mor 30 4 Dum Dum MALANCHA,2.5 NO AIRPORT GATE Dum Dum Swami Swarupananda Sarani, Kol- 31 6 Airport 79 INCINERATOR RD,DUMDUM 32 17 Dum Dum CANTT S P MUKHERJEE RD, DUMDUM 33 19 Dum Dum CANTT 34 19 Birati, Khalisakota Pally Dum Dum 35 36 10 Kabi Satyan dutta road Nimta 37 12 Birati, Nimta, Pathanpur Nimta North Dum Dum 38 21 Srinagar,Durganagar, Birati,Kol-51 Nimta Parts of Purba Alipur (near Gangulybari), 39 Nimta 27, 28, 33 Nimta BL No.