DOCSLIB.ORG

Comet/Asteroid Orbit Determination and Ephemeris Software (CODES)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Comet/Asteroid Orbit Determination and Ephemeris Software (CODES) CComet/asteroid OOrbit DDetermination and EEphemeris SSoftware by Jim Baer 1 CODES In support of current minor planet surveys, CODES combines an n-body numerical integrator with a Graphical User Interface to provide the following capabilities: l Orbit determination based on optical and radar observations; l Calculation of topocentric or geocentric ephemerides; l Identification of known minor planets which most closely match a set of observations; l Linear and non-linear collision analysis. l N-body integrator accounts for cometary thrusting (if applicable), solar radiation pressure, solar oblateness, and gravitational perturbations (including relativistic effects) from the Sun, nine planets, Earth's Moon, and up to 300 asteroids. 2 CODES CODES is an object-oriented application Level One Menu: • Create, Delete, or Open instances of the class “MinorPlanet” Level Two Menu: • Add attributes (observations) • Derive additional attributes (orbital elements, ephemerides, collision analysis) 3 CODES Level One Menu 4 CODES Level Two Menu 5 CODES Level Two Menu: Designate the minor planet as a comet or asteroid l Should be the first change made to a new minor planet file l Critically impacts: – Least-squares best-fit orbit – Processing visual magnitude data – Minor Planet Center (MPC) catalog search – Orbital element display – Use of cometary thrust in numerical integrator 6 CODES Level Two Menu: Adding an Observation l Manual entry of ground-based optical observation l Manual entry of radar observation l Parse and process Minor Planet Electronic Circular (MPEC) or Minor Planet Center Observation (MPCOBS) file l Parse and process Near Earth Object Dynamic Site (NEODyS) ASCII observation file l If International Earth Rotation Service (IERS) Earth Orientation Parameter (EOP) file not available for observation epoch, manual entry or default EOPs used note: observations supported in period 1900-2200 7 CODES Level Two Menu: Review/Delete Existing Observations 8 CODES Level Two Menu: Compute/Evaluate/Propogate the orbit of this minor planet 9 CODES Level Two Menu: Compute an initial two-body orbit l Gauss Method l Conditioned Gauss (semi-major axis constrained) l Laplace Method l Herget's Method (slant-range constrained) l Statistical Ranging (slant-range sampling) (Note: This algorithm is located in a different menu, but is a highly- effective method of initial orbit determination, especially for very short arcs) 10 CODES Level Two Menu: Compute an initial two-body orbit (results) 11 CODES Level Two Menu: Compute an n-body best-fit orbit • Least squares with n-body numerical integration – cometary thrusting (if applicable) – solar radiation pressure – solar oblateness – gravitational perturbations (including relativistic terms) from the Sun, nine planets, Earth's Moon, and up to 300 asteroids l Refines – an initial two-body orbit – a statistical ranging orbit – an imported orbit (MPCORBcr file) – a user-specified orbit l Allows observations to be excluded based on excessive chi or residuals 12 CODES Level Two Menu: Compute an n-body best-fit orbit (results) l state vector plus covariances l derived orbital elements plus covariances l residuals for each observation l visual absolute magnitude and slope parameter (if apparent magnitude observations are available) l estimate of the minor planet's radius (asteroids only, if visual absolute magnitude and slope parameter are available) l Minimum Orbital Intersection Distance (NEOs only) l Warning for Potentially-Hazardous Objects l SkyMorph parameters formatted for easy input l output to screen and text file 13 CODES Level Two Menu: Sample Valid Orbits: Observational Monte Carlo l If least-squares converges but observed arc is very short, the covariance ellipsoid may not accurately represent the solution space; this option directly samples the space of valid orbits – Add Gaussian uncertainty to each observation – Apply least-squares to derive variant orbit – Default setting: Create 100 variant orbits l Variant orbits can be displayed in color-coded scatterplots to illustrate solution space – q vs. e – q vs. i – q vs. w – q vs. W – q vs. M l Variant orbits can be used – to generate ephemeris scatterplots for precovery/recovery – for Monte Carlo collision analysis 14 CODES Level Two Menu: Sample Valid Orbits: Observational Monte Carlo (cont) 15 CODES Level Two Menu: Sample Valid Orbits: Statistical Ranging l Used for very short arcs in place of initial-orbit methods; directly samples the non-linear space of valid orbits – Randomly generate slant ranges for first and last observations (based on user-specified min/max slant range) – Combine with first/last observations and observer positions to create two position vectors – Use Gauss sector-triangle ratios (two-body) or Herget’s method (n- body) to derive state vector – Compare predicted RA/Decs to observations; accept if RMS residual less than user-specified threshold l User can optionally require only prograde, elliptical orbits l User-specified number of variants generated 16 CODES Level Two Menu: Sample Valid Orbits: Statistical Ranging (cont.) 17 CODES Level Two Menu: Sample Valid Orbits: Statistical Ranging (cont.) l Variant orbits can be – displayed in color-coded scatterplots to illustrate non-linear solution space – used to generate ephemeris scatterplots for precovery/recovery – used for Monte Carlo collision analysis l Only reliable approach for very short-arc cases – Reveals multiple solutions – Robust orbit and ephemeris uncertainty spaces – Allows collision analysis when no best-fit orbit is available 18 CODES Level Two Menu: Compute the observational residuals resulting from the current orbit 19 CODES Level Two Menu: Propogate the current orbit to a new epoch 20 CODES Level Two Menu: Display Current Orbit 21 CODES Level Two Menu: Manually specify an orbit for this minor planet • User can specify either state vector or orbital elements (plus covariances) • Allows evaluation or adoption of non-CODES derived orbits • Calculate residuals for comparison • Provide initial orbit for best-fit refinement • Calculate an ephemeris • Conduct a linear collision analysis • Allows trial and error determination of DT cometary thrust parameter 22 CODES Level Two Menu: Import a minor planet orbit from the MPCORBcr or COMET catalogs Allows CODES to read the orbital elements of a minor planet directly from the appropriate MPC catalog: • Provide initial orbit for best-fit refinement • Add estimated covariances • Add or determine cometary thrust parameters • Calculate an ephemeris • Conduct a collision analysis 23 CODES Level Two Menu: Compare observations to positions of known minor planets Generates a list of those minor planets in the MPCORBcr or COMET catalog most nearly matching the observations of this minor planet • Use two-body or n-body mechanics • Select "medium" or "high" integration accuracy • Narrow n-body asteroid candidate search on basis of • population (NEA, main belt, Centaur/TNO) • absolute magnitude For each entry: • Extracts orbital elements from catalog • Predicts astrometric position at time of each observation • Eliminated if either • RMS residual > 3 degrees • visual mag. residual > 2 Candidates output to screen and text file 24 CODES Level Two Menu: Generate an optical ephemeris l Geocentric/topocentric ephemerides for desired range of dates l Tabular presentation – nominal values for each desired date – major axis/minor axis/orientation angle of linear covariance ellipse l Scatterplot presentation – displays predicted RA/Decs based on variant orbits generated by Observational Monte Carlo or Statistical Ranging – Color-coded by RMS residual of variant orbit to illustrate most likely positions – Displays non-linear observation space for precovery/recovery 25 CODES Level Two Menu: Generate an optical ephemeris (cont) 26 CODES Level Two Menu: Generate an optical ephemeris (cont) 27 CODES Level Two Menu: Linear Collision Analysis Requires state vector and (if impact probability desired) covariances Algorithm: l Propogate state vector forward from epoch to desired end-point – at end of each integration step, test distance to each possible target (Sun, Moon, nine major planets) • if (distance < target radius) => collision – use bisection to isolate – propogate covariances to determine impact probability • else if (distance > target radius) and (distance < user-specified threshold) and (first derivative changes sign) – use bisection to isolate minimum – if (distance at minimum < target radius) => collision • use bisection to isolate • propogate covariances to determine impact probability – if (distance at minimum > target radius) => near miss • propogate covariances to determine impact probability 28 CODES Level Two Menu: Non-Linear Collision Analysis Primary options requires state vector and covariances, plus all observations Algorithm: l Creates user-specified number of Virtual Asteroids – Distributed normally in observation space about the nominal state vector – Spaced along the Line of Variations l Each VA propogated forward from epoch to desired end-point – collisions/near-misses noted as in linear analysis – events with ((scaled moid - 3-sigma width of covariance ellipse) < threshold) are sorted by target, date, and stretching into trails • The minimum approach or folding point for each trail is retained – use differential correction to test for collision/near-miss – if differential correction fails, or in case of an interrupted return, create a “dense sampling” (100 VAs around minimum/folding point), look for collision/nearest
Load more

Recommended publications
  • Orbit Determination Methods and Techniques
    PROJECTE FINAL DE CARRERA (PFC) GEOSAR Mission: Orbit Determination Methods and Techniques Marc Fernàndez Uson PFC Advisor: Prof. Antoni Broquetas Ibars May 2016 PROJECTE FINAL DE CARRERA (PFC) GEOSAR Mission: Orbit Determination Methods and Techniques Marc Fernàndez Uson ABSTRACT ABSTRACT Multiple applications such as land stability control, natural risks prevention or accurate numerical weather prediction models from water vapour atmospheric mapping would substantially benefit from permanent radar monitoring given their fast evolution is not observable with present Low Earth Orbit based systems. In order to overcome this drawback, GEOstationary Synthetic Aperture Radar missions (GEOSAR) are presently being studied. GEOSAR missions are based on operating a radar payload hosted by a communication satellite in a geostationary orbit. Due to orbital perturbations, the satellite does not follow a perfectly circular orbit, but has a slight eccentricity and inclination that can be used to form the synthetic aperture required to obtain images. Several sources affect the along-track phase history in GEOSAR missions causing unwanted fluctuations which may result in image defocusing. The main expected contributors to azimuth phase noise are orbit determination errors, radar carrier frequency drifts, the Atmospheric Phase Screen (APS), and satellite attitude instabilities and structural vibration. In order to obtain an accurate image of the scene after SAR processing, the range history of every point of the scene must be known. This fact requires a high precision orbit modeling and the use of suitable techniques for atmospheric phase screen compensation, which are well beyond the usual orbit determination requirement of satellites in GEO orbits. The other influencing factors like oscillator drift and attitude instability, vibration, etc., must be controlled or compensated.
    [Show full text]
  • Electric Propulsion System Scaling for Asteroid Capture-And-Return Missions
    Electric propulsion system scaling for asteroid capture-and-return missions Justin M. Little⇤ and Edgar Y. Choueiri† Electric Propulsion and Plasma Dynamics Laboratory, Princeton University, Princeton, NJ, 08544 The requirements for an electric propulsion system needed to maximize the return mass of asteroid capture-and-return (ACR) missions are investigated in detail. An analytical model is presented for the mission time and mass balance of an ACR mission based on the propellant requirements of each mission phase. Edelbaum’s approximation is used for the Earth-escape phase. The asteroid rendezvous and return phases of the mission are modeled as a low-thrust optimal control problem with a lunar assist. The numerical solution to this problem is used to derive scaling laws for the propellant requirements based on the maneuver time, asteroid orbit, and propulsion system parameters. Constraining the rendezvous and return phases by the synodic period of the target asteroid, a semi- empirical equation is obtained for the optimum specific impulse and power supply. It was found analytically that the optimum power supply is one such that the mass of the propulsion system and power supply are approximately equal to the total mass of propellant used during the entire mission. Finally, it is shown that ACR missions, in general, are optimized using propulsion systems capable of processing 100 kW – 1 MW of power with specific impulses in the range 5,000 – 10,000 s, and have the potential to return asteroids on the order of 103 104 tons. − Nomenclature
    [Show full text]
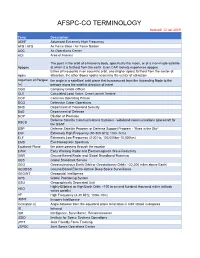
  • AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019
    AFSPC-CO TERMINOLOGY Revised: 12 Jan 2019 Term Description AEHF Advanced Extremely High Frequency AFB / AFS Air Force Base / Air Force Station AOC Air Operations Center AOI Area of Interest The point in the orbit of a heavenly body, specifically the moon, or of a man-made satellite Apogee at which it is farthest from the earth. Even CAP rockets experience apogee. Either of two points in an eccentric orbit, one (higher apsis) farthest from the center of Apsis attraction, the other (lower apsis) nearest to the center of attraction Argument of Perigee the angle in a satellites' orbit plane that is measured from the Ascending Node to the (ω) perigee along the satellite direction of travel CGO Company Grade Officer CLV Calculated Load Value, Crew Launch Vehicle COP Common Operating Picture DCO Defensive Cyber Operations DHS Department of Homeland Security DoD Department of Defense DOP Dilution of Precision Defense Satellite Communications Systems - wideband communications spacecraft for DSCS the USAF DSP Defense Satellite Program or Defense Support Program - "Eyes in the Sky" EHF Extremely High Frequency (30-300 GHz; 1mm-1cm) ELF Extremely Low Frequency (3-30 Hz; 100,000km-10,000km) EMS Electromagnetic Spectrum Equitorial Plane the plane passing through the equator EWR Early Warning Radar and Electromagnetic Wave Resistivity GBR Ground-Based Radar and Global Broadband Roaming GBS Global Broadcast Service GEO Geosynchronous Earth Orbit or Geostationary Orbit ( ~22,300 miles above Earth) GEODSS Ground-Based Electro-Optical Deep Space Surveillance
    [Show full text]
  • Orbit Determination Using Modern Filters/Smoothers and Continuous Thrust Modeling
    Orbit Determination Using Modern Filters/Smoothers and Continuous Thrust Modeling by Zachary James Folcik B.S. Computer Science Michigan Technological University, 2000 SUBMITTED TO THE DEPARTMENT OF AERONAUTICS AND ASTRONAUTICS IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE IN AERONAUTICS AND ASTRONAUTICS AT THE MASSACHUSETTS INSTITUTE OF TECHNOLOGY JUNE 2008 © 2008 Massachusetts Institute of Technology. All rights reserved. Signature of Author:_______________________________________________________ Department of Aeronautics and Astronautics May 23, 2008 Certified by:_____________________________________________________________ Dr. Paul J. Cefola Lecturer, Department of Aeronautics and Astronautics Thesis Supervisor Certified by:_____________________________________________________________ Professor Jonathan P. How Professor, Department of Aeronautics and Astronautics Thesis Advisor Accepted by:_____________________________________________________________ Professor David L. Darmofal Associate Department Head Chair, Committee on Graduate Students 1 [This page intentionally left blank.] 2 Orbit Determination Using Modern Filters/Smoothers and Continuous Thrust Modeling by Zachary James Folcik Submitted to the Department of Aeronautics and Astronautics on May 23, 2008 in Partial Fulfillment of the Requirements for the Degree of Master of Science in Aeronautics and Astronautics ABSTRACT The development of electric propulsion technology for spacecraft has led to reduced costs and longer lifespans for certain
    [Show full text]
  • Orbit and Spin
    Orbit and Spin Overview: A whole-body activity that explores the relative sizes, distances, orbit, and spin of the Sun, Earth, and Moon. Target Grade Level: 3-5 Estimated Duration: 2 40-minute sessions Learning Goals: Students will be able to… • compare the relative sizes of the Earth, Moon, and Sun. • contrast the distance between the Earth and Moon to the distance between the Earth and Sun. • differentiate between the motions of orbit and spin. • demonstrate the spins of the Earth and the Moon, as well as the orbits of the Earth around the Sun, and the Moon around the Earth. Standards Addressed: Benchmarks (AAAS, 1993) The Physical Setting, 4A: The Universe, 4B: The Earth National Science Education Standards (NRC, 1996) Physical Science, Standard B: Position and motion of objects Earth and Space Science, Standard D: Objects in the sky, Changes in Earth and sky Table of Contents: Background Page 1 Materials and Procedure 5 What I Learned… Science Journal Page 14 Earth Picture 15 Sun Picture 16 Moon Picture 17 Earth Spin Demonstration 18 Moon Orbit Demonstration 19 Extensions and Adaptations 21 Standards Addressed, detailed 22 Background: Sun The Sun is the center of our Solar System, both literally—as all of the planets orbit around it, and figuratively—as its rays warm our planet and sustain life as we know it. The Sun is very hot compared to temperatures we usually encounter. Its mean surface temperature is about 9980° Fahrenheit (5800 Kelvin) and its interior temperature is as high as about 28 million° F (15,500,000 Kelvin).
    [Show full text]
  • Analysis of Transfer Maneuvers from Initial
    Revista Mexicana de Astronom´ıa y Astrof´ısica, 52, 283–295 (2016) ANALYSIS OF TRANSFER MANEUVERS FROM INITIAL CIRCULAR ORBIT TO A FINAL CIRCULAR OR ELLIPTIC ORBIT M. A. Sharaf1 and A. S. Saad2,3 Received March 14 2016; accepted May 16 2016 RESUMEN Presentamos un an´alisis de las maniobras de transferencia de una ´orbita circu- lar a una ´orbita final el´ıptica o circular. Desarrollamos este an´alisis para estudiar el problema de las transferencias impulsivas en las misiones espaciales. Consideramos maniobras planas usando ecuaciones reci´enobtenidas; con estas ecuaciones se com- paran las maniobras circulares y el´ıpticas. Esta comparaci´on es importante para el dise˜no´optimo de misiones espaciales, y permite obtener mapeos ´utiles para mostrar cu´al es la mejor maniobra. Al respecto, desarrollamos este tipo de comparaciones mediante 10 resultados, y los mostramos gr´aficamente. ABSTRACT In the present paper an analysis of the transfer maneuvers from initial circu- lar orbit to a final circular or elliptic orbit was developed to study the problem of impulsive transfers for space missions. It considers planar maneuvers using newly derived equations. With these equations, comparisons of circular and elliptic ma- neuvers are made. This comparison is important for the mission designers to obtain useful mappings showing where one maneuver is better than the other. In this as- pect, we developed this comparison throughout ten results, together with some graphs to show their meaning. Key Words: celestial mechanics — methods: analytical — space vehicles 1. INTRODUCTION The large amount of information from interplanetary missions, such as Pioneer (Dyer et al.
    [Show full text]
  • Statistical Orbit Determination
    Preface The modem field of orbit determination (OD) originated with Kepler's inter­ pretations of the observations made by Tycho Brahe of the planetary motions. Based on the work of Kepler, Newton was able to establish the mathematical foundation of celestial mechanics. During the ensuing centuries, the efforts to im­ prove the understanding of the motion of celestial bodies and artificial satellites in the modem era have been a major stimulus in areas of mathematics, astronomy, computational methodology and physics. Based on Newton's foundations, early efforts to determine the orbit were focused on a deterministic approach in which a few observations, distributed across the sky during a single arc, were used to find the position and velocity vector of a celestial body at some epoch. This uniquely categorized the orbit. Such problems are deterministic in the sense that they use the same number of independent observations as there are unknowns. With the advent of daily observing programs and the realization that the or­ bits evolve continuously, the foundation of modem precision orbit determination evolved from the attempts to use a large number of observations to determine the orbit. Such problems are over-determined in that they utilize far more observa­ tions than the number required by the deterministic approach. The development of the digital computer in the decade of the 1960s allowed numerical approaches to supplement the essentially analytical basis for describing the satellite motion and allowed a far more rigorous representation of the force models that affect the motion. This book is based on four decades of classroom instmction and graduate- level research.
    [Show full text]
  • Strategy for Human Spaceflight In
    Developing the sustainable foundations for returning Americans to the Moon and enabling a new era of commercial spaceflight in low Earth orbit (LEO) are the linchpins of our national human spaceflight policy. As we work to return Americans to the Moon, we plan to do so in partnership with other nations. We will therefore coordinate our lunar exploration strategy with our ISS partners while maintaining and expanding our partnerships in LEO. As we work to create a new set of commercial human spaceflight capabilities, we will enable U.S. commercial enterprises to develop and operate under principles of long-term sustainability for space activity and recognize that their success cannot depend on Federal funding and programs alone. The National Space Council recognized the need for such a national strategy for human spaceflight in LEO and economic growth in space, and in February of 2018, called on NASA, the Department of State, and the Department of Commerce to work together to develop one. This strategy follows the direction established by the Administration through Space Policy Directives 1, 2, and 3, which created an innovative new framework for American leadership by reinvigorating America’s human exploration of the Moon and Mars; streamlining regulations on the commercial use of space; and establishing the first national policy for space traffic management. Our strategy for the future of human spaceflight in LEO and for economic growth in space will operate within the context of these directives. Through interagency dialogue, and in coordination with the Executive Office of the President, we have further defined our overarching goals for human spaceflight in LEO as follows: 1.
    [Show full text]
  • Sun-Synchronous Satellites
    Topic: Sun-synchronous Satellites Course: Remote Sensing and GIS (CC-11) M.A. Geography (Sem.-3) By Dr. Md. Nazim Professor, Department of Geography Patna College, Patna University Lecture-3 Concept: Orbits and their Types: Any object that moves around the Earth has an orbit. An orbit is the path that a satellite follows as it revolves round the Earth. The plane in which a satellite always moves is called the orbital plane and the time taken for completing one orbit is called orbital period. Orbit is defined by the following three factors: 1. Shape of the orbit, which can be either circular or elliptical depending upon the eccentricity that gives the shape of the orbit, 2. Altitude of the orbit which remains constant for a circular orbit but changes continuously for an elliptical orbit, and 3. Angle that an orbital plane makes with the equator. Depending upon the angle between the orbital plane and equator, orbits can be categorised into three types - equatorial, inclined and polar orbits. Different orbits serve different purposes. Each has its own advantages and disadvantages. There are several types of orbits: 1. Polar 2. Sunsynchronous and 3. Geosynchronous Field of View (FOV) is the total view angle of the camera, which defines the swath. When a satellite revolves around the Earth, the sensor observes a certain portion of the Earth’s surface. Swath or swath width is the area (strip of land of Earth surface) which a sensor observes during its orbital motion. Swaths vary from one sensor to another but are generally higher for space borne sensors (ranging between tens and hundreds of kilometers wide) in comparison to airborne sensors.
    [Show full text]
  • Multiple Solutions for Asteroid Orbits: Computational Procedure and Applications
    A&A 431, 729–746 (2005) Astronomy DOI: 10.1051/0004-6361:20041737 & c ESO 2005 Astrophysics Multiple solutions for asteroid orbits: Computational procedure and applications A. Milani1,M.E.Sansaturio2,G.Tommei1, O. Arratia2, and S. R. Chesley3 1 Dipartimento di Matematica, Università di Pisa, via Buonarroti 2, 56127 Pisa, Italy e-mail: [milani;tommei]@mail.dm.unipi.it 2 E.T.S. de Ingenieros Industriales, University of Valladolid Paseo del Cauce 47011 Valladolid, Spain e-mail: [meusan;oscarr]@eis.uva.es 3 Jet Propulsion Laboratory, 4800 Oak Grove Drive, CA-91109 Pasadena, USA e-mail: [email protected] Received 27 July 2004 / Accepted 20 October 2004 Abstract. We describe the Multiple Solutions Method, a one-dimensional sampling of the six-dimensional orbital confidence region that is widely applicable in the field of asteroid orbit determination. In many situations there is one predominant direction of uncertainty in an orbit determination or orbital prediction, i.e., a “weak” direction. The idea is to record Multiple Solutions by following this, typically curved, weak direction, or Line Of Variations (LOV). In this paper we describe the method and give new insights into the mathematics behind this tool. We pay particular attention to the problem of how to ensure that the coordinate systems are properly scaled so that the weak direction really reflects the intrinsic direction of greatest uncertainty. We also describe how the multiple solutions can be used even in the absence of a nominal orbit solution, which substantially broadens the realm of applications. There are numerous applications for multiple solutions; we discuss a few problems in asteroid orbit determination and prediction where we have had good success with the method.
    [Show full text]
  • On-Orbit Assembly of Space Assets: a Path to Affordable and Adaptable Space Infrastructure
    CENTER FOR SPACE POLICY AND STRATEGY FEBRUARY 2018 ON-ORBIT ASSEMBLY OF SPACE ASSETS: A PATH TO AFFORDABLE AND ADAPTABLE SPACE INFRASTRUCTURE DANIELLE PISKORZ AND KAREN L. JONES THE AEROSPACE CORPORATION © 2018 The Aerospace Corporation. All trademarks, service marks, and trade names contained herein are the property of their respective owners. Approved for public release; distribution unlimited. OTR201800234 DANIELLE PISKORZ Dr. Danielle Piskorz is a member of the technical staff in The Aerospace Corporation’s Visual and Infrared Sensor Systems Department. She provides data and mission performance analysis in the area of space situational awareness. Her space policy experience derives from positions at the Science and Technology Policy Institute and the National Academies of Sciences, Engineering, and Medicine, where she contributed to a broad range of projects in commercial and civil space. She holds a Ph.D. in planetary science from the California Institute of Technology and a B.S. in physics from Massachusetts Institute of Technology. KAREN L. JONES Karen Jones is a senior project leader with The Aerospace Corporation’s Center for Space Policy and Strategy. She has experience and expertise in the disciplines of technology strategy, program evaluation, and regulatory and policy analysis spanning the public sector, telecommunications, aerospace defense, energy, and environmental industries. She has an M.B.A. from the Yale School of Management. CONTRIBUTORS The authors would like to acknowledge contributions from Roy Nakagawa, Henry Helvajian, and Thomas Heinsheimer of The Aerospace Corporation and David Barnhart of the University of Southern California. ABOUT THE CENTER FOR SPACE POLICY AND STRATEGY The Center for Space Policy and Strategy is a specialized research branch within The Aerospace Corporation, a nonprofit organization that operates a federally funded research and development center providing objective technical analysis for programs of national significance.
    [Show full text]
  • SATELLITES ORBIT ELEMENTS : EPHEMERIS, Keplerian ELEMENTS, STATE VECTORS
    www.myreaders.info www.myreaders.info Return to Website SATELLITES ORBIT ELEMENTS : EPHEMERIS, Keplerian ELEMENTS, STATE VECTORS RC Chakraborty (Retd), Former Director, DRDO, Delhi & Visiting Professor, JUET, Guna, www.myreaders.info, [email protected], www.myreaders.info/html/orbital_mechanics.html, Revised Dec. 16, 2015 (This is Sec. 5, pp 164 - 192, of Orbital Mechanics - Model & Simulation Software (OM-MSS), Sec 1 to 10, pp 1 - 402.) OM-MSS Page 164 OM-MSS Section - 5 -------------------------------------------------------------------------------------------------------43 www.myreaders.info SATELLITES ORBIT ELEMENTS : EPHEMERIS, Keplerian ELEMENTS, STATE VECTORS Satellite Ephemeris is Expressed either by 'Keplerian elements' or by 'State Vectors', that uniquely identify a specific orbit. A satellite is an object that moves around a larger object. Thousands of Satellites launched into orbit around Earth. First, look into the Preliminaries about 'Satellite Orbit', before moving to Satellite Ephemeris data and conversion utilities of the OM-MSS software. (a) Satellite : An artificial object, intentionally placed into orbit. Thousands of Satellites have been launched into orbit around Earth. A few Satellites called Space Probes have been placed into orbit around Moon, Mercury, Venus, Mars, Jupiter, Saturn, etc. The Motion of a Satellite is a direct consequence of the Gravity of a body (earth), around which the satellite travels without any propulsion. The Moon is the Earth's only natural Satellite, moves around Earth in the same kind of orbit. (b) Earth Gravity and Satellite Motion : As satellite move around Earth, it is pulled in by the gravitational force (centripetal) of the Earth. Contrary to this pull, the rotating motion of satellite around Earth has an associated force (centrifugal) which pushes it away from the Earth.
    [Show full text]