Identifying Loci Under Positive Selection in Complex Population Histories
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Variation in Protein Coding Genes Identifies Information
bioRxiv preprint doi: https://doi.org/10.1101/679456; this version posted June 21, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Animal complexity and information flow 1 1 2 3 4 5 Variation in protein coding genes identifies information flow as a contributor to 6 animal complexity 7 8 Jack Dean, Daniela Lopes Cardoso and Colin Sharpe* 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Institute of Biological and Biomedical Sciences 25 School of Biological Science 26 University of Portsmouth, 27 Portsmouth, UK 28 PO16 7YH 29 30 * Author for correspondence 31 [email protected] 32 33 Orcid numbers: 34 DLC: 0000-0003-2683-1745 35 CS: 0000-0002-5022-0840 36 37 38 39 40 41 42 43 44 45 46 47 48 49 Abstract bioRxiv preprint doi: https://doi.org/10.1101/679456; this version posted June 21, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Animal complexity and information flow 2 1 Across the metazoans there is a trend towards greater organismal complexity. How 2 complexity is generated, however, is uncertain. Since C.elegans and humans have 3 approximately the same number of genes, the explanation will depend on how genes are 4 used, rather than their absolute number. -

Identification of Potential Key Genes and Pathway Linked with Sporadic Creutzfeldt-Jakob Disease Based on Integrated Bioinformatics Analyses
medRxiv preprint doi: https://doi.org/10.1101/2020.12.21.20248688; this version posted December 24, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted medRxiv a license to display the preprint in perpetuity. All rights reserved. No reuse allowed without permission. Identification of potential key genes and pathway linked with sporadic Creutzfeldt-Jakob disease based on integrated bioinformatics analyses Basavaraj Vastrad1, Chanabasayya Vastrad*2 , Iranna Kotturshetti 1. Department of Biochemistry, Basaveshwar College of Pharmacy, Gadag, Karnataka 582103, India. 2. Biostatistics and Bioinformatics, Chanabasava Nilaya, Bharthinagar, Dharwad 580001, Karanataka, India. 3. Department of Ayurveda, Rajiv Gandhi Education Society`s Ayurvedic Medical College, Ron, Karnataka 562209, India. * Chanabasayya Vastrad [email protected] Ph: +919480073398 Chanabasava Nilaya, Bharthinagar, Dharwad 580001 , Karanataka, India NOTE: This preprint reports new research that has not been certified by peer review and should not be used to guide clinical practice. medRxiv preprint doi: https://doi.org/10.1101/2020.12.21.20248688; this version posted December 24, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted medRxiv a license to display the preprint in perpetuity. All rights reserved. No reuse allowed without permission. Abstract Sporadic Creutzfeldt-Jakob disease (sCJD) is neurodegenerative disease also called prion disease linked with poor prognosis. The aim of the current study was to illuminate the underlying molecular mechanisms of sCJD. The mRNA microarray dataset GSE124571 was downloaded from the Gene Expression Omnibus database. Differentially expressed genes (DEGs) were screened. -

Supplementary Materials
Supplementary materials Supplementary Table S1: MGNC compound library Ingredien Molecule Caco- Mol ID MW AlogP OB (%) BBB DL FASA- HL t Name Name 2 shengdi MOL012254 campesterol 400.8 7.63 37.58 1.34 0.98 0.7 0.21 20.2 shengdi MOL000519 coniferin 314.4 3.16 31.11 0.42 -0.2 0.3 0.27 74.6 beta- shengdi MOL000359 414.8 8.08 36.91 1.32 0.99 0.8 0.23 20.2 sitosterol pachymic shengdi MOL000289 528.9 6.54 33.63 0.1 -0.6 0.8 0 9.27 acid Poricoic acid shengdi MOL000291 484.7 5.64 30.52 -0.08 -0.9 0.8 0 8.67 B Chrysanthem shengdi MOL004492 585 8.24 38.72 0.51 -1 0.6 0.3 17.5 axanthin 20- shengdi MOL011455 Hexadecano 418.6 1.91 32.7 -0.24 -0.4 0.7 0.29 104 ylingenol huanglian MOL001454 berberine 336.4 3.45 36.86 1.24 0.57 0.8 0.19 6.57 huanglian MOL013352 Obacunone 454.6 2.68 43.29 0.01 -0.4 0.8 0.31 -13 huanglian MOL002894 berberrubine 322.4 3.2 35.74 1.07 0.17 0.7 0.24 6.46 huanglian MOL002897 epiberberine 336.4 3.45 43.09 1.17 0.4 0.8 0.19 6.1 huanglian MOL002903 (R)-Canadine 339.4 3.4 55.37 1.04 0.57 0.8 0.2 6.41 huanglian MOL002904 Berlambine 351.4 2.49 36.68 0.97 0.17 0.8 0.28 7.33 Corchorosid huanglian MOL002907 404.6 1.34 105 -0.91 -1.3 0.8 0.29 6.68 e A_qt Magnogrand huanglian MOL000622 266.4 1.18 63.71 0.02 -0.2 0.2 0.3 3.17 iolide huanglian MOL000762 Palmidin A 510.5 4.52 35.36 -0.38 -1.5 0.7 0.39 33.2 huanglian MOL000785 palmatine 352.4 3.65 64.6 1.33 0.37 0.7 0.13 2.25 huanglian MOL000098 quercetin 302.3 1.5 46.43 0.05 -0.8 0.3 0.38 14.4 huanglian MOL001458 coptisine 320.3 3.25 30.67 1.21 0.32 0.9 0.26 9.33 huanglian MOL002668 Worenine -

Bioinformatics Approach to Probe Protein-Protein Interactions
Virginia Commonwealth University VCU Scholars Compass Theses and Dissertations Graduate School 2013 Bioinformatics Approach to Probe Protein-Protein Interactions: Understanding the Role of Interfacial Solvent in the Binding Sites of Protein-Protein Complexes;Network Based Predictions and Analysis of Human Proteins that Play Critical Roles in HIV Pathogenesis. Mesay Habtemariam Virginia Commonwealth University Follow this and additional works at: https://scholarscompass.vcu.edu/etd Part of the Bioinformatics Commons © The Author Downloaded from https://scholarscompass.vcu.edu/etd/2997 This Thesis is brought to you for free and open access by the Graduate School at VCU Scholars Compass. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of VCU Scholars Compass. For more information, please contact [email protected]. ©Mesay A. Habtemariam 2013 All Rights Reserved Bioinformatics Approach to Probe Protein-Protein Interactions: Understanding the Role of Interfacial Solvent in the Binding Sites of Protein-Protein Complexes; Network Based Predictions and Analysis of Human Proteins that Play Critical Roles in HIV Pathogenesis. A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science at Virginia Commonwealth University. By Mesay Habtemariam B.Sc. Arbaminch University, Arbaminch, Ethiopia 2005 Advisors: Glen Eugene Kellogg, Ph.D. Associate Professor, Department of Medicinal Chemistry & Institute For Structural Biology And Drug Discovery Danail Bonchev, Ph.D., D.SC. Professor, Department of Mathematics and Applied Mathematics, Director of Research in Bioinformatics, Networks and Pathways at the School of Life Sciences Center for the Study of Biological Complexity. Virginia Commonwealth University Richmond, Virginia May 2013 ኃይልን በሚሰጠኝ በክርስቶስ ሁሉን እችላለሁ:: ፊልጵስዩስ 4:13 I can do all this through God who gives me strength. -

Dynamic Clonal Progression in Xenografts of Acute Lymphoblastic Leukemia with Intrachromosomal Amplification of Chromosome 21
Acute Lymphoblastic Leukemia SUPPLEMENTARY APPENDIX Dynamic clonal progression in xenografts of acute lymphoblastic leukemia with intrachromosomal amplification of chromosome 21 Paul. B. Sinclair, 1 Helen H. Blair, 1 Sarra L. Ryan, 1 Lars Buechler, 1 Joanna Cheng, 1 Jake Clayton, 1 Rebecca Hanna, 1 Shaun Hollern, 1 Zoe Hawking, 1 Matthew Bashton, 1 Claire J. Schwab, 1 Lisa Jones, 1 Lisa J. Russell, 1 Helen Marr, 1 Peter Carey, 2 Christina Halsey, 3 Olaf Heidenreich, 1 Anthony V. Moorman 1 and Christine J. Harrison 1 1Wolfson Childhood Cancer Research Centre, Northern Institute for Cancer Research, Newcastle University, Newcastle-upon-Tyne; 2Depart - ment of Clinical Haematology, Royal Victoria Infirmary, Newcastle-upon-Tyne and 3Wolfson Wohl Cancer Research Centre, Institute of Cancer Sciences, University of Glasgow, UK ©2018 Ferrata Storti Foundation. This is an open-access paper. doi:10.3324/haematol. 2017.172304 Received: May 15, 2017. Accepted: February 8, 2018. Pre-published: February 15, 2018. Correspondence: [email protected] Supplementary methods Determination of xenograft experimental end points. Mice were checked daily for signs of ill health and routinely weighed once a week or more often if indicated. Mice were culled at end stage disease as defined by; weight gain of >20%, weight loss reaching 20% at any time or >10% maintained for 72 hours compared with weight at the start of the experiment, starey coat, porphyrin staining of eyes and nose or sunken eyes, persistent skin tenting, immobility, unresponsive or very aggressive behaviour, loss of upright stance, laboured respiration, blood staining or other discharge, signs of anaemia including extreme paleness of feet, tail and ears. -

Identi Cation and Validation of an RNA Binding Proteins-Associated
Identication and Validation of an RNA Binding Proteins-Associated Prognostic Signature for Non- Small Cell Lung Cancer Ti-wei Miao sichuan university https://orcid.org/0000-0003-3705-1568 Fang-ying Chen Department of Tuberculosis, the Third People's Hospital of Tibet Autonomous Region, Lhasa, China Wei Xiao Respiratory Group, Department of Integrated Traditional Chinese and Western Medicine, West China Hospital, Sichuan University, Chengdu, China Long-yi Du Respiratory Group, Department of Integrated Traditional Chinese and Western Medicine, West China Hospital, Sichuan University, Chengdu, China Bing Mao Respiratory Group, Department of Integrated Traditional Chinese and Western Medicine, West China Hospital, Sichuan University, Chengdu, China Yan Wang Research Core Facility, West China Hospital, Sichuan University, Chengdu, China Juan-juan Fu ( [email protected] ) Respiratory Group, Department of Integrated Traditional Chinese and Western Medicine, West China Hospital, Sichuan University, Chengdu, China https://orcid.org/0000-0002-7957-1409 Research Keywords: RBPs, NSCLC, prognosis, meta-analysis, bioinformatics Posted Date: November 4th, 2020 DOI: https://doi.org/10.21203/rs.3.rs-100245/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Page 1/27 Abstract Background: Non-small cell lung cancer (NSCLC) is a malignancy with relatively high incidence and poor prognosis. RNA-binding proteins (RBPs) were reported to be dysregulated in multiple cancers and were closely associated with tumor initiation and progression. However, the functions of RBPs in NSCLC remain unclear. Method: The RNA sequencing data and corresponding clinical information of NSCLC was downloaded from The Cancer Genome Atlas (TCGA) database. -

Protein Tyrosine Phosphorylation in Haematopoietic Cancers and the Functional Significance of Phospho- Lyn SH2 Domain
Protein Tyrosine Phosphorylation in Haematopoietic Cancers and the Functional Significance of Phospho- Lyn SH2 Domain By Lily Li Jin A thesis submitted in conformity with the requirements for the degree of Ph.D. in Molecular Genetics, Graduate Department of Molecular Genetics, in the University of Toronto © Copyright by Lily Li Jin (2015) Protein Tyrosine Phosphorylation in Haematopoietic Cancers and the Functional Significance of Phospho-Lyn SH2 Domain Lily Li Jin 2015 Ph.D. in Molecular Genetics Graduate Department of Molecular Genetics University of Toronto Abstract Protein-tyrosine phosphorylation (pY) is a minor but important protein post-translational modification that modulates a wide range of cellular functions and is involved in cancer. Dysregulation of tyrosine kinases (TKs) and protein-tyrosine phosphatases (PTPs) have been observed in multiple myeloma (MM) and acute myeloid leukemia (AML) and is a subject of study. Using recently developed mass spectrometry-based proteomics techniques, quantitative PTP expression and cellular pY profiles were generated for MM cell lines and mouse xenograft tumors, as well as primary AML samples. Integrated comprehensive analyses on these data implicated a subset of TKs and PTPs in MM and AML, with valuable insights gained on the dynamic regulation of pY in biological systems. In particular, I propose a model that describes the cellular pY state as a functional output of the total activated TKs and PTPs in the cell. My results show that the global pY profile in the cancer models is quantitatively related to the cellular levels of activated TKs and PTPs. Furthermore, the identity of the implicated TK/PTPs is system- ii dependent, demonstrating context-dependent regulation of pY. -

In Hepatocellular Carcinoma Metabolism
Molecular BioSystems Accepted Manuscript This is an Accepted Manuscript, which has been through the Royal Society of Chemistry peer review process and has been accepted for publication. Accepted Manuscripts are published online shortly after acceptance, before technical editing, formatting and proof reading. Using this free service, authors can make their results available to the community, in citable form, before we publish the edited article. We will replace this Accepted Manuscript with the edited and formatted Advance Article as soon as it is available. You can find more information about Accepted Manuscripts in the Information for Authors. Please note that technical editing may introduce minor changes to the text and/or graphics, which may alter content. The journal’s standard Terms & Conditions and the Ethical guidelines still apply. In no event shall the Royal Society of Chemistry be held responsible for any errors or omissions in this Accepted Manuscript or any consequences arising from the use of any information it contains. www.rsc.org/molecularbiosystems Page 1 of 32 Molecular BioSystems Table of contents entry We reconstructed Hepatitis C Virus assembly reactions to find host-target metabolites impeding this reaction. Manuscript Accepted BioSystems Molecular Molecular BioSystems Page 2 of 32 1 Systems biology analysis of hepatitis C virus infection reveals 2 the role of copy number increases in regions of chromosome 1q 3 in hepatocellular carcinoma metabolism 4 5 Ibrahim E. Elsemman 1, 2,5 , Adil Mardinoglu 1,3 , Saeed Shoaie -

Processing, Modification and Anticodon–Codon
biomolecules Review Factors That Shape Eukaryotic tRNAomes: Processing, Modification and Anticodon–Codon Use Richard J. Maraia 1,2,* and Aneeshkumar G. Arimbasseri 3,* 1 Intramural Research Program, Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health, Bethesda, MD 20892, USA 2 Commissioned Corps, U.S. Public Health Service, Rockville, MD 20016, USA 3 Molecular Genetics Laboratory, National Institute of Immunology, Aruna Asaf Ali Marg, New Delhi 110067, India * Correspondence: [email protected] (R.J.M.); [email protected] (A.G.A.) Academic Editor: Valérie de Crécy-Lagard Received: 9 January 2017; Accepted: 24 February 2017; Published: 8 March 2017 Abstract: Transfer RNAs (tRNAs) contain sequence diversity beyond their anticodons and the large variety of nucleotide modifications found in all kingdoms of life. Some modifications stabilize structure and fit in the ribosome whereas those to the anticodon loop modulate messenger RNA (mRNA) decoding activity more directly. The identities of tRNAs with some universal anticodon loop modifications vary among distant and parallel species, likely to accommodate fine tuning for their translation systems. This plasticity in positions 34 (wobble) and 37 is reflected in codon use bias. Here, we review convergent evidence that suggest that expansion of the eukaryotic tRNAome was supported by its dedicated RNA polymerase III transcription system and coupling to the precursor-tRNA chaperone, La protein. We also review aspects of eukaryotic tRNAome evolution involving G34/A34 anticodon-sparing, relation to A34 modification to inosine, biased codon use and regulatory information in the redundancy (synonymous) component of the genetic code. We then review interdependent anticodon loop modifications involving position 37 in 3 eukaryotes. -
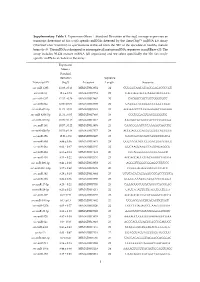
Supplementary Table 1. Expression
Supplementary Table 1. Expression (Mean Standard Deviation of the log2 average expression or transcript detection) of Sus scrofa specific miRNAs detected by the GeneChip™ miRNA 4.0 Array (ThermoFisher Scientific) in spermatozoa retrieved from the SRF of the ejaculate of healthy mature boars (n=3). The miRNA is designed to interrogate all mature miRNA sequences in miRBase v20. The array includes 30.424 mature miRNA (all organisms) and we select specifically the 326 Sus scrofa- specific miRNAs included in the array. Expression Mean ± Standard Deviation Sequence Transcript ID (log2) Accession Length Sequence ssc-miR-1285 13.98 ± 0.13 MIMAT0013954 24 CUGGGCAACAUAGCGAGACCCCGU ssc-miR-16 12.6 ± 0.74 MIMAT0007754 22 UAGCAGCACGUAAAUAUUGGCG ssc-miR-4332 12.32 ± 0.29 MIMAT0017962 20 CACGGCCGCCGCCGGGCGCC ssc-miR-92a 12.06 ± 0.09 MIMAT0013908 22 UAUUGCACUUGUCCCGGCCUGU ssc-miR-671-5p 11.73 ± 0.54 MIMAT0025381 24 AGGAAGCCCUGGAGGGGCUGGAGG ssc-miR-4334-5p 11.31 ± 0.05 MIMAT0017966 19 CCCUGGAGUGACGGGGGUG ssc-miR-425-5p 10.99 ± 0.15 MIMAT0013917 23 AAUGACACGAUCACUCCCGUUGA ssc-miR-191 10.57 ± 0.22 MIMAT0013876 23 CAACGGAAUCCCAAAAGCAGCUG ssc-miR-92b-5p 10.53 ± 0.18 MIMAT0017377 24 AGGGACGGGACGCGGUGCAGUGUU ssc-miR-15b 10.01 ± 0.9 MIMAT0002125 22 UAGCAGCACAUCAUGGUUUACA ssc-miR-30d 9.89 ± 0.36 MIMAT0013871 24 UGUAAACAUCCCCGACUGGAAGCU ssc-miR-26a 9.62 ± 0.47 MIMAT0002135 22 UUCAAGUAAUCCAGGAUAGGCU ssc-miR-484 9.55 ± 0.14 MIMAT0017974 20 CCCAGGGGGCGACCCAGGCU ssc-miR-103 9.53 ± 0.22 MIMAT0002154 23 AGCAGCAUUGUACAGGGCUAUGA ssc-miR-296-3p 9.41 ± 0.26 MIMAT0022958 -

Coexpression Networks Based on Natural Variation in Human Gene Expression at Baseline and Under Stress
University of Pennsylvania ScholarlyCommons Publicly Accessible Penn Dissertations Fall 2010 Coexpression Networks Based on Natural Variation in Human Gene Expression at Baseline and Under Stress Renuka Nayak University of Pennsylvania, [email protected] Follow this and additional works at: https://repository.upenn.edu/edissertations Part of the Computational Biology Commons, and the Genomics Commons Recommended Citation Nayak, Renuka, "Coexpression Networks Based on Natural Variation in Human Gene Expression at Baseline and Under Stress" (2010). Publicly Accessible Penn Dissertations. 1559. https://repository.upenn.edu/edissertations/1559 This paper is posted at ScholarlyCommons. https://repository.upenn.edu/edissertations/1559 For more information, please contact [email protected]. Coexpression Networks Based on Natural Variation in Human Gene Expression at Baseline and Under Stress Abstract Genes interact in networks to orchestrate cellular processes. Here, we used coexpression networks based on natural variation in gene expression to study the functions and interactions of human genes. We asked how these networks change in response to stress. First, we studied human coexpression networks at baseline. We constructed networks by identifying correlations in expression levels of 8.9 million gene pairs in immortalized B cells from 295 individuals comprising three independent samples. The resulting networks allowed us to infer interactions between biological processes. We used the network to predict the functions of poorly-characterized human genes, and provided some experimental support. Examining genes implicated in disease, we found that IFIH1, a diabetes susceptibility gene, interacts with YES1, which affects glucose transport. Genes predisposing to the same diseases are clustered non-randomly in the network, suggesting that the network may be used to identify candidate genes that influence disease susceptibility. -

TARBP1 CRISPR/Cas9 KO Plasmid (H): Sc-411029
SANTA CRUZ BIOTECHNOLOGY, INC. TARBP1 CRISPR/Cas9 KO Plasmid (h): sc-411029 BACKGROUND APPLICATIONS The Clustered Regularly Interspaced Short Palindromic Repeats (CRISPR) and TARBP1 CRISPR/Cas9 KO Plasmid (h) is recommended for the disruption of CRISPR-associated protein (Cas9) system is an adaptive immune response gene expression in human cells. defense mechanism used by archea and bacteria for the degradation of 20 nt non-coding RNA sequence: guides Cas9 foreign genetic material (4,6). This mechanism can be repurposed for other to a specific target location in the genomic DNA functions, including genomic engineering for mammalian systems, such as U6 promoter: drives gRNA scaffold: helps Cas9 gene knockout (KO) (1,2,3,5). CRISPR/Cas9 KO Plasmid products enable the expression of gRNA bind to target DNA identification and cleavage of specific genes by utilizing guide RNA (gRNA) sequences derived from the Genome-scale CRISPR Knock-Out (GeCKO) v2 Termination signal Green Fluorescent library developed in the Zhang Laboratory at the Broad Institute (3,5). Protein: to visually verify transfection CRISPR/Cas9 Knockout Plasmid CBh (chicken β-Actin REFERENCES hybrid) promoter: drives expression of Cas9 1. Cong, L., et al. 2013. Multiplex genome engineering using CRISPR/Cas 2A peptide: allows production of both systems. Science 339: 819-823. Cas9 and GFP from the same CBh promoter 2. Mali, P., et al. 2013. RNA-guided human genome engineering via Cas9. Nuclear localization signal Science 339: 823-826. Nuclear localization signal SpCas9 ribonuclease 3. Ran, F.A., et al. 2013. Genome engineering using the CRISPR-Cas9 system. Nat. Protoc. 8: 2281-2308.