Reducibility and Completeness
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

CS601 DTIME and DSPACE Lecture 5 Time and Space Functions: T, S
CS601 DTIME and DSPACE Lecture 5 Time and Space functions: t, s : N → N+ Definition 5.1 A set A ⊆ U is in DTIME[t(n)] iff there exists a deterministic, multi-tape TM, M, and a constant c, such that, 1. A = L(M) ≡ w ∈ U M(w)=1 , and 2. ∀w ∈ U, M(w) halts within c · t(|w|) steps. Definition 5.2 A set A ⊆ U is in DSPACE[s(n)] iff there exists a deterministic, multi-tape TM, M, and a constant c, such that, 1. A = L(M), and 2. ∀w ∈ U, M(w) uses at most c · s(|w|) work-tape cells. (Input tape is “read-only” and not counted as space used.) Example: PALINDROMES ∈ DTIME[n], DSPACE[n]. In fact, PALINDROMES ∈ DSPACE[log n]. [Exercise] 1 CS601 F(DTIME) and F(DSPACE) Lecture 5 Definition 5.3 f : U → U is in F (DTIME[t(n)]) iff there exists a deterministic, multi-tape TM, M, and a constant c, such that, 1. f = M(·); 2. ∀w ∈ U, M(w) halts within c · t(|w|) steps; 3. |f(w)|≤|w|O(1), i.e., f is polynomially bounded. Definition 5.4 f : U → U is in F (DSPACE[s(n)]) iff there exists a deterministic, multi-tape TM, M, and a constant c, such that, 1. f = M(·); 2. ∀w ∈ U, M(w) uses at most c · s(|w|) work-tape cells; 3. |f(w)|≤|w|O(1), i.e., f is polynomially bounded. (Input tape is “read-only”; Output tape is “write-only”. -

Interactive Proof Systems and Alternating Time-Space Complexity
Theoretical Computer Science 113 (1993) 55-73 55 Elsevier Interactive proof systems and alternating time-space complexity Lance Fortnow” and Carsten Lund** Department of Computer Science, Unicersity of Chicago. 1100 E. 58th Street, Chicago, IL 40637, USA Abstract Fortnow, L. and C. Lund, Interactive proof systems and alternating time-space complexity, Theoretical Computer Science 113 (1993) 55-73. We show a rough equivalence between alternating time-space complexity and a public-coin interactive proof system with the verifier having a polynomial-related time-space complexity. Special cases include the following: . All of NC has interactive proofs, with a log-space polynomial-time public-coin verifier vastly improving the best previous lower bound of LOGCFL for this model (Fortnow and Sipser, 1988). All languages in P have interactive proofs with a polynomial-time public-coin verifier using o(log’ n) space. l All exponential-time languages have interactive proof systems with public-coin polynomial-space exponential-time verifiers. To achieve better bounds, we show how to reduce a k-tape alternating Turing machine to a l-tape alternating Turing machine with only a constant factor increase in time and space. 1. Introduction In 1981, Chandra et al. [4] introduced alternating Turing machines, an extension of nondeterministic computation where the Turing machine can make both existential and universal moves. In 1985, Goldwasser et al. [lo] and Babai [l] introduced interactive proof systems, an extension of nondeterministic computation consisting of two players, an infinitely powerful prover and a probabilistic polynomial-time verifier. The prover will try to convince the verifier of the validity of some statement. -

Week 1: an Overview of Circuit Complexity 1 Welcome 2
Topics in Circuit Complexity (CS354, Fall’11) Week 1: An Overview of Circuit Complexity Lecture Notes for 9/27 and 9/29 Ryan Williams 1 Welcome The area of circuit complexity has a long history, starting in the 1940’s. It is full of open problems and frontiers that seem insurmountable, yet the literature on circuit complexity is fairly large. There is much that we do know, although it is scattered across several textbooks and academic papers. I think now is a good time to look again at circuit complexity with fresh eyes, and try to see what can be done. 2 Preliminaries An n-bit Boolean function has domain f0; 1gn and co-domain f0; 1g. At a high level, the basic question asked in circuit complexity is: given a collection of “simple functions” and a target Boolean function f, how efficiently can f be computed (on all inputs) using the simple functions? Of course, efficiency can be measured in many ways. The most natural measure is that of the “size” of computation: how many copies of these simple functions are necessary to compute f? Let B be a set of Boolean functions, which we call a basis set. The fan-in of a function g 2 B is the number of inputs that g takes. (Typical choices are fan-in 2, or unbounded fan-in, meaning that g can take any number of inputs.) We define a circuit C with n inputs and size s over a basis B, as follows. C consists of a directed acyclic graph (DAG) of s + n + 2 nodes, with n sources and one sink (the sth node in some fixed topological order on the nodes). -

The Complexity Zoo
The Complexity Zoo Scott Aaronson www.ScottAaronson.com LATEX Translation by Chris Bourke [email protected] 417 classes and counting 1 Contents 1 About This Document 3 2 Introductory Essay 4 2.1 Recommended Further Reading ......................... 4 2.2 Other Theory Compendia ............................ 5 2.3 Errors? ....................................... 5 3 Pronunciation Guide 6 4 Complexity Classes 10 5 Special Zoo Exhibit: Classes of Quantum States and Probability Distribu- tions 110 6 Acknowledgements 116 7 Bibliography 117 2 1 About This Document What is this? Well its a PDF version of the website www.ComplexityZoo.com typeset in LATEX using the complexity package. Well, what’s that? The original Complexity Zoo is a website created by Scott Aaronson which contains a (more or less) comprehensive list of Complexity Classes studied in the area of theoretical computer science known as Computa- tional Complexity. I took on the (mostly painless, thank god for regular expressions) task of translating the Zoo’s HTML code to LATEX for two reasons. First, as a regular Zoo patron, I thought, “what better way to honor such an endeavor than to spruce up the cages a bit and typeset them all in beautiful LATEX.” Second, I thought it would be a perfect project to develop complexity, a LATEX pack- age I’ve created that defines commands to typeset (almost) all of the complexity classes you’ll find here (along with some handy options that allow you to conveniently change the fonts with a single option parameters). To get the package, visit my own home page at http://www.cse.unl.edu/~cbourke/. -

Midterm Study Sheet for CS3719 Regular Languages and Finite
Midterm study sheet for CS3719 Regular languages and finite automata: • An alphabet is a finite set of symbols. Set of all finite strings over an alphabet Σ is denoted Σ∗.A language is a subset of Σ∗. Empty string is called (epsilon). • Regular expressions are built recursively starting from ∅, and symbols from Σ and closing under ∗ Union (R1 ∪ R2), Concatenation (R1 ◦ R2) and Kleene Star (R denoting 0 or more repetitions of R) operations. These three operations are called regular operations. • A Deterministic Finite Automaton (DFA) D is a 5-tuple (Q, Σ, δ, q0,F ), where Q is a finite set of states, Σ is the alphabet, δ : Q × Σ → Q is the transition function, q0 is the start state, and F is the set of accept states. A DFA accepts a string if there exists a sequence of states starting with r0 = q0 and ending with rn ∈ F such that ∀i, 0 ≤ i < n, δ(ri, wi) = ri+1. The language of a DFA, denoted L(D) is the set of all and only strings that D accepts. • Deterministic finite automata are used in string matching algorithms such as Knuth-Morris-Pratt algorithm. • A language is called regular if it is recognized by some DFA. • ‘Theorem: The class of regular languages is closed under union, concatenation and Kleene star operations. • A non-deterministic finite automaton (NFA) is a 5-tuple (Q, Σ, δ, q0,F ), where Q, Σ, q0 and F are as in the case of DFA, but the transition function δ is δ : Q × (Σ ∪ {}) → P(Q). -

Sharp Lower Bounds for the Dimension of Linearizations of Matrix Polynomials∗
Electronic Journal of Linear Algebra ISSN 1081-3810 A publication of the International Linear Algebra Society Volume 17, pp. 518-531, November 2008 ELA SHARP LOWER BOUNDS FOR THE DIMENSION OF LINEARIZATIONS OF MATRIX POLYNOMIALS∗ FERNANDO DE TERAN´ † AND FROILAN´ M. DOPICO‡ Abstract. A standard way of dealing with matrixpolynomial eigenvalue problems is to use linearizations. Byers, Mehrmann and Xu have recently defined and studied linearizations of dimen- sions smaller than the classical ones. In this paper, lower bounds are provided for the dimensions of linearizations and strong linearizations of a given m × n matrixpolynomial, and particular lineariza- tions are constructed for which these bounds are attained. It is also proven that strong linearizations of an n × n regular matrixpolynomial of degree must have dimension n × n. Key words. Matrixpolynomials, Matrixpencils, Linearizations, Dimension. AMS subject classifications. 15A18, 15A21, 15A22, 65F15. 1. Introduction. We will say that a matrix polynomial of degree ≥ 1 −1 P (λ)=λ A + λ A−1 + ···+ λA1 + A0, (1.1) m×n where A0,A1,...,A ∈ C and A =0,is regular if m = n and det P (λ)isnot identically zero as a polynomial in λ. We will say that P (λ)issingular otherwise. A linearization of P (λ)isamatrix pencil L(λ)=λX + Y such that there exist unimod- ular matrix polynomials, i.e., matrix polynomials with constant nonzero determinant, of appropriate dimensions, E(λ)andF (λ), such that P (λ) 0 E(λ)L(λ)F (λ)= , (1.2) 0 Is where Is denotes the s × s identity matrix. Classically s =( − 1) min{m, n}, but recently linearizations of smaller dimension have been considered [3]. -

Chapter 6 Formal Language Theory
Chapter 6 Formal Language Theory In this chapter, we introduce formal language theory, the computational theories of languages and grammars. The models are actually inspired by formal logic, enriched with insights from the theory of computation. We begin with the definition of a language and then proceed to a rough characterization of the basic Chomsky hierarchy. We then turn to a more de- tailed consideration of the types of languages in the hierarchy and automata theory. 6.1 Languages What is a language? Formally, a language L is defined as as set (possibly infinite) of strings over some finite alphabet. Definition 7 (Language) A language L is a possibly infinite set of strings over a finite alphabet Σ. We define Σ∗ as the set of all possible strings over some alphabet Σ. Thus L ⊆ Σ∗. The set of all possible languages over some alphabet Σ is the set of ∗ all possible subsets of Σ∗, i.e. 2Σ or ℘(Σ∗). This may seem rather simple, but is actually perfectly adequate for our purposes. 6.2 Grammars A grammar is a way to characterize a language L, a way to list out which strings of Σ∗ are in L and which are not. If L is finite, we could simply list 94 CHAPTER 6. FORMAL LANGUAGE THEORY 95 the strings, but languages by definition need not be finite. In fact, all of the languages we are interested in are infinite. This is, as we showed in chapter 2, also true of human language. Relating the material of this chapter to that of the preceding two, we can view a grammar as a logical system by which we can prove things. -

Complexity Theory
Complexity Theory Course Notes Sebastiaan A. Terwijn Radboud University Nijmegen Department of Mathematics P.O. Box 9010 6500 GL Nijmegen the Netherlands [email protected] Copyright c 2010 by Sebastiaan A. Terwijn Version: December 2017 ii Contents 1 Introduction 1 1.1 Complexity theory . .1 1.2 Preliminaries . .1 1.3 Turing machines . .2 1.4 Big O and small o .........................3 1.5 Logic . .3 1.6 Number theory . .4 1.7 Exercises . .5 2 Basics 6 2.1 Time and space bounds . .6 2.2 Inclusions between classes . .7 2.3 Hierarchy theorems . .8 2.4 Central complexity classes . 10 2.5 Problems from logic, algebra, and graph theory . 11 2.6 The Immerman-Szelepcs´enyi Theorem . 12 2.7 Exercises . 14 3 Reductions and completeness 16 3.1 Many-one reductions . 16 3.2 NP-complete problems . 18 3.3 More decision problems from logic . 19 3.4 Completeness of Hamilton path and TSP . 22 3.5 Exercises . 24 4 Relativized computation and the polynomial hierarchy 27 4.1 Relativized computation . 27 4.2 The Polynomial Hierarchy . 28 4.3 Relativization . 31 4.4 Exercises . 32 iii 5 Diagonalization 34 5.1 The Halting Problem . 34 5.2 Intermediate sets . 34 5.3 Oracle separations . 36 5.4 Many-one versus Turing reductions . 38 5.5 Sparse sets . 38 5.6 The Gap Theorem . 40 5.7 The Speed-Up Theorem . 41 5.8 Exercises . 43 6 Randomized computation 45 6.1 Probabilistic classes . 45 6.2 More about BPP . 48 6.3 The classes RP and ZPP . -
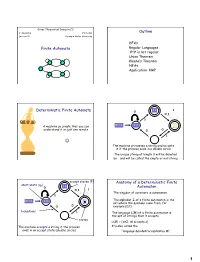
Deterministic Finite Automata 0 0,1 1
Great Theoretical Ideas in CS V. Adamchik CS 15-251 Outline Lecture 21 Carnegie Mellon University DFAs Finite Automata Regular Languages 0n1n is not regular Union Theorem Kleene’s Theorem NFAs Application: KMP 11 1 Deterministic Finite Automata 0 0,1 1 A machine so simple that you can 0111 111 1 ϵ understand it in just one minute 0 0 1 The machine processes a string and accepts it if the process ends in a double circle The unique string of length 0 will be denoted by ε and will be called the empty or null string accept states (F) Anatomy of a Deterministic Finite start state (q0) 11 0 Automaton 0,1 1 The singular of automata is automaton. 1 The alphabet Σ of a finite automaton is the 0111 111 1 ϵ set where the symbols come from, for 0 0 example {0,1} transitions 1 The language L(M) of a finite automaton is the set of strings that it accepts states L(M) = {x∈Σ: M accepts x} The machine accepts a string if the process It’s also called the ends in an accept state (double circle) “language decided/accepted by M”. 1 The Language L(M) of Machine M The Language L(M) of Machine M 0 0 0 0,1 1 q 0 q1 q0 1 1 What language does this DFA decide/accept? L(M) = All strings of 0s and 1s The language of a finite automaton is the set of strings that it accepts L(M) = { w | w has an even number of 1s} M = (Q, Σ, , q0, F) Q = {q0, q1, q2, q3} Formal definition of DFAs where Σ = {0,1} A finite automaton is a 5-tuple M = (Q, Σ, , q0, F) q0 Q is start state Q is the finite set of states F = {q1, q2} Q accept states : Q Σ → Q transition function Σ is the alphabet : Q Σ → Q is the transition function q 1 0 1 0 1 0,1 q0 Q is the start state q0 q0 q1 1 q q1 q2 q2 F Q is the set of accept states 0 M q2 0 0 q2 q3 q2 q q q 1 3 0 2 L(M) = the language of machine M q3 = set of all strings machine M accepts EXAMPLE Determine the language An automaton that accepts all recognized by and only those strings that contain 001 1 0,1 0,1 0 1 0 0 0 1 {0} {00} {001} 1 L(M)={1,11,111, …} 2 Membership problem Determine the language decided by Determine whether some word belongs to the language. -

Arxiv:Quant-Ph/0202111V1 20 Feb 2002
Quantum statistical zero-knowledge John Watrous Department of Computer Science University of Calgary Calgary, Alberta, Canada [email protected] February 19, 2002 Abstract In this paper we propose a definition for (honest verifier) quantum statistical zero-knowledge interactive proof systems and study the resulting complexity class, which we denote QSZK. We prove several facts regarding this class: The following natural problem is a complete promise problem for QSZK: given instructions • for preparing two mixed quantum states, are the states close together or far apart in the trace norm metric? By instructions for preparing a mixed quantum state we mean the description of a quantum circuit that produces the mixed state on some specified subset of its qubits, assuming all qubits are initially in the 0 state. This problem is a quantum generalization of the complete promise problem of Sahai| i and Vadhan [33] for (classical) statistical zero-knowledge. QSZK is closed under complement. • QSZK PSPACE. (At present it is not known if arbitrary quantum interactive proof • systems⊆ can be simulated in PSPACE, even for one-round proof systems.) Any honest verifier quantum statistical zero-knowledge proof system can be parallelized to • a two-message (i.e., one-round) honest verifier quantum statistical zero-knowledge proof arXiv:quant-ph/0202111v1 20 Feb 2002 system. (For arbitrary quantum interactive proof systems it is known how to parallelize to three messages, but not two.) Moreover, the one-round proof system can be taken to be such that the prover sends only one qubit to the verifier in order to achieve completeness and soundness error exponentially close to 0 and 1/2, respectively. -

Delegating Computation: Interactive Proofs for Muggles∗
Electronic Colloquium on Computational Complexity, Revision 1 of Report No. 108 (2017) Delegating Computation: Interactive Proofs for Muggles∗ Shafi Goldwasser Yael Tauman Kalai Guy N. Rothblum MIT and Weizmann Institute Microsoft Research Weizmann Institute [email protected] [email protected] [email protected] Abstract In this work we study interactive proofs for tractable languages. The (honest) prover should be efficient and run in polynomial time, or in other words a \muggle".1 The verifier should be super-efficient and run in nearly-linear time. These proof systems can be used for delegating computation: a server can run a computation for a client and interactively prove the correctness of the result. The client can verify the result's correctness in nearly-linear time (instead of running the entire computation itself). Previously, related questions were considered in the Holographic Proof setting by Babai, Fortnow, Levin and Szegedy, in the argument setting under computational assumptions by Kilian, and in the random oracle model by Micali. Our focus, however, is on the original inter- active proof model where no assumptions are made on the computational power or adaptiveness of dishonest provers. Our main technical theorem gives a public coin interactive proof for any language computable by a log-space uniform boolean circuit with depth d and input length n. The verifier runs in time n · poly(d; log(n)) and space O(log(n)), the communication complexity is poly(d; log(n)), and the prover runs in time poly(n). In particular, for languages computable by log-space uniform NC (circuits of polylog(n) depth), the prover is efficient, the verifier runs in time n · polylog(n) and space O(log(n)), and the communication complexity is polylog(n). -

5.2 Intractable Problems -- NP Problems
Algorithms for Data Processing Lecture VIII: Intractable Problems–NP Problems Alessandro Artale Free University of Bozen-Bolzano [email protected] of Computer Science http://www.inf.unibz.it/˜artale 2019/20 – First Semester MSc in Computational Data Science — UNIBZ Some material (text, figures) displayed in these slides is courtesy of: Alberto Montresor, Werner Nutt, Kevin Wayne, Jon Kleinberg, Eva Tardos. A. Artale Algorithms for Data Processing Definition. P = set of decision problems for which there exists a poly-time algorithm. Problems and Algorithms – Decision Problems The Complexity Theory considers so called Decision Problems. • s Decision• Problem. X Input encoded asX a finite“yes” binary string ; • Decision ProblemA : Is conceived asX a set of strings on whichs the answer to the decision problem is ; yes if s ∈ X Algorithm for a decision problemA s receives an input string , and no if s 6∈ X ( ) = A. Artale Algorithms for Data Processing Problems and Algorithms – Decision Problems The Complexity Theory considers so called Decision Problems. • s Decision• Problem. X Input encoded asX a finite“yes” binary string ; • Decision ProblemA : Is conceived asX a set of strings on whichs the answer to the decision problem is ; yes if s ∈ X Algorithm for a decision problemA s receives an input string , and no if s 6∈ X ( ) = Definition. P = set of decision problems for which there exists a poly-time algorithm. A. Artale Algorithms for Data Processing Towards NP — Efficient Verification • • The issue here is the3-SAT contrast between finding a solution Vs. checking a proposed solution.I ConsiderI for example : We do not know a polynomial-time algorithm to find solutions; but Checking a proposed solution can be easily done in polynomial time (just plug 0/1 and check if it is a solution).