DOCSLIB.ORG

Solutions to the Exercises

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Solutions to the Exercises Solutions to the Exercises Chapter 1 Solution 1.1 (a) Your computer may be programmed to allocate borderline cases to the next group down, or the next group up; and it may or may not manage to follow this rule consistently, depending on its handling of the numbers involved. Following a rule which says 'move borderline cases to the next group up', these are the five classifications. (i) 1.0-1.2 1.2-1.4 1.4-1.6 1.6-1.8 1.8-2.0 2.0-2.2 2.2-2.4 6 6 4 8 4 3 4 2.4-2.6 2.6-2.8 2.8-3.0 3.0-3.2 3.2-3.4 3.4-3.6 3.6-3.8 6 3 2 2 0 1 1 (ii) 1.0-1.3 1.3-1.6 1.6-1.9 1.9-2.2 2.2-2.5 10 6 10 5 6 2.5-2.8 2.8-3.1 3.1-3.4 3.4-3.7 7 3 1 2 (iii) 0.8-1.1 1.1-1.4 1.4-1.7 1.7-2.0 2.0-2.3 2 10 6 10 7 2.3-2.6 2.6-2.9 2.9-3.2 3.2-3.5 3.5-3.8 6 4 3 1 1 (iv) 0.85-1.15 1.15-1.45 1.45-1.75 1.75-2.05 2.05-2.35 4 9 8 9 5 2.35-2.65 2.65-2.95 2.95-3.25 3.25-3.55 3.55-3.85 7 3 3 1 1 (V) 0.9-1.2 1.2-1.5 1.5-1.8 1.8-2.1 2.1-2.4 6 7 11 7 4 2.4-2.7 2.7-3.0 3.0-3.3 3.3-3.6 3.6-3.9 7 4 2 1 1 (b) Computer graphics: the diagrams are shown in Figures 1.9 to 1.11. Solution 1.2 (a) Computer graphics: see Figure 1.12. (b) Computer graphics: see Figure 1.13. If your computer gives graphics that are text-character based (otherwise known as low-resolution graphics) then the scatter plots you obtain will not be as precise as those appearing in the text and the fitted line will not be displayed. However, the main message of the data should still be apparent. Elements of Statistics Solution 1.3 (a) In order of decreasing brain weight to body weight ratio, the species are as follows. Species Body weight Brain weight Ratio Rhesus Monkey Mole Human Mouse Potar Monkey Chimpanzee Hamster Cat Rat Mountain Beaver Guinea Pig Rabbit Goat Grey Wolf Sheep Donkey Gorilla Asian Elephant Kangaroo Jaguar Giraffe Horse Pig Cow African Elephant Triceratops Diplodocus Brachiosaurus (b) (i) Computer graphics: see Figure 1.14. (ii) Computer graphics: see Figure 1.15. Solution 1.4 There were 23 children who survived the condition. Their birth weights are 1.130, 1.410, 1.575, 1.680, 1.715, 1.720, 1.760, 1.930, 2.015, 2.040, 2.090, 2.200, 2.400, 2.550, 2.570, 2.600, 2.700, 2.830, 2.950, 3.005, 3.160, 3.400, 3.640. The median birth weight for these children is 2.200 kg (the 12th value in the sorted list). There were 27 children who died. The sorted birth weights are 1.030, 1.050, 1.100, 1.175, 1.185, 1.225, 1.230, 1.262, 1.295, 1.300, 1.310, 1.500, 1.550, 1.600, 1.720, 1.750, 1.770, 1.820, 1.890, 1.940, 2.200, 2.270, 2.275, 2.440, 2.500, 2.560, 2.730. The middle value is the 14th (thirteen either side) so the median birth weight for these children who died is 1.600 kg. Solutions to Exercises Solution 1.5 The ordered differences are 3.8, 10.3, 11.8, 12.9, 17.5, 20.5, 20.6, 24.4, 25.3, 28.4, 30.6. The median difference is 20.5. Solution 1.6 Once the data are entered, most computers will return the sample median at a single command. It is 79.7 inches. Solution 1.7 (a) The mean birth weight of the 23 infants who survived SIRDS is 1.130 + 1.575 + . + 3.005 53.070 -xs = --- = 2.307 kg; Notice the subscripts S, D and T 23 23 used in this solution to label and the mean birth weight of the 27 infants who died is distinguish the three sample means. It was not strictly - 1.050 + 1.175 + . + 2.730 - 45.680 necessary to do this here, since we XD = - -= 1.692 kg. 27 27 will not be referring to these The mean birth weight of the entire sample is numbers again in this exercise, but it is a convenient labelling system when a statistical analysis becomes more complicated. Solution 1.8 The mean 'After - Before' difference in ~able'l.11is - 25.3 + 20.5 + . + 28.4 206.1 X = - -= 18.74 pmol/l. 11 11 Solution 1.9 The mean snowfall over the 63 years was 80.3 inches. Solution 1.10 (a) The lower quartile birth weight for the 27 children who died is given by 4~ = x(+(n+l))= x(7) = 1.230kg; the upper quartile birth weight is = x(;(,+~))= ~(21)= 2.200kg. (b) For these silica data, the sample size is n = 22. The lower quartile is qL = x(;(n+l))= X(?) = x(5;) which is three-quarters of the way between x(~)= 26.39 and X(G) = 27.08. This is say, 26.9. The sample median is m=x(5(n+l)) 1 = = x(~l$), which is midway between x(ll) = 28.69 and = 29.36. This is 29.025; say, 29.0. Elements of Statistics The upper quartile is Qa = X($(,+,)) = X(?) = x(17a), one-quarter of the way between ~(17)= 33.28 and x(18) = 33.40. This is qv = 33.28 + i(33.40 - 33.28) = i(33.28) + a(33.40) = 33.31; say, 33.3. Solution 1.1 1 For the snowfall data the lower and upper quartiles are q~ = 63.6 inches and qu = 98.3 inches respectively. The interquartile range is qu - q~ = 34.7 inches. Solution 1.12 Answering these questions might involve delving around for the instruction manual that came with your calculator! The important thing is not to use the formula-let your calculator do all the arithmetic. All you should need to do is key in the original data and then press the correct button. (There might be a choice, one of which is when the divisor in the 'standard deviation' formula is n, the other is when the divisor is n - 1. Remember, in this course we use the second formula.) (a) You should have obtained s = 8.33, to two decimal places. (b) The standard deviation for the silica data is s = 4.29. (c) For the collapsed runners' ,L? endorphin concentrations, s = 98.0. Solution 1.13 (a) The standard deviation s is 0.66 kg. (b) The standard deviation s is 23.7ikhes. Solution 1.14 Summary measures for this data set are x(~)= 23, q~ = 34, m = 45, q~ = 62, = 83. The sample median is m = 45; the sample mean is 31 = 48.4; the sample standard deviation is 18.1. The range is 83 - 23 = 60; the interquartile range is 62 - 34 = 28. Solution 1.15 The first group contains 19 completed families. Some summary statistics are m = 10, Z = 8.2, s = 5.2, interquartile range = 10. For the second group of 35 completed families, summary statistics are m = 4, = 4.8, s = 4.0, interquartile range = 4. The differences are very noticeable between the two groups. Mothers educated for the longer time period would appear to have smaller families. In each case the mean and median are of comparable size. For the smaller group, the interquartile range is much greater than the standard deviation. If the three or four very large families are removed from the second data set, the differences become even more pronounced. Solutions to Exercises Solution 1.16 (a) The five-figure summary for the silica data is given by A convenient scale sufficient to cover the extent of the data is from 20 to 40. The i.q.r. is 33.31 - 26.91 = 6.40. Then and this exceeds the sample maximum, so the upper adjacent value is the sample maximum itself, 34.82. Also This value is less than the sample minimurn, so the lower adjacent value is the sample minimum itself. For these data there are no extreme values. The boxplot is shown in Figure S1.l. Percentage silica Figure S1.1 (b) For the snowfall data the lower adjacent value is 39.8; the minimum is 25.0. The upper adjacent value is equal to the maximum, 126.4. The boxplot is shown in Figure S1.2. Annual snowfall (inches) Figure S1.2 Solution 1.1 7 The sample skewness for the first group of mothers is -0.29. Solution 1.18 (a) The five-figure summaries for the three groups are normal: (14, 92, 124.5, 274.75, 655) alloxan-diabetic: (13, 70.25,139.5, 276, 499) insulin-treated: (18, 44, 82, 133, 465). The normal group has one very high recording at 655; the next highest is 455, which is more consistent with the other two groups.
Load more

Recommended publications
  • The Beta-Binomial Distribution Introduction Bayesian Derivation
    In Danish: 2005-09-19 / SLB Translated: 2008-05-28 / SLB Bayesian Statistics, Simulation and Software The beta-binomial distribution I have translated this document, written for another course in Danish, almost as is. I have kept the references to Lee, the textbook used for that course. Introduction In Lee: Bayesian Statistics, the beta-binomial distribution is very shortly mentioned as the predictive distribution for the binomial distribution, given the conjugate prior distribution, the beta distribution. (In Lee, see pp. 78, 214, 156.) Here we shall treat it slightly more in depth, partly because it emerges in the WinBUGS example in Lee x 9.7, and partly because it possibly can be useful for your project work. Bayesian Derivation We make n independent Bernoulli trials (0-1 trials) with probability parameter π. It is well known that the number of successes x has the binomial distribution. Considering the probability parameter π unknown (but of course the sample-size parameter n is known), we have xjπ ∼ bin(n; π); where in generic1 notation n p(xjπ) = πx(1 − π)1−x; x = 0; 1; : : : ; n: x We assume as prior distribution for π a beta distribution, i.e. π ∼ beta(α; β); 1By this we mean that p is not a fixed function, but denotes the density function (in the discrete case also called the probability function) for the random variable the value of which is argument for p. 1 with density function 1 p(π) = πα−1(1 − π)β−1; 0 < π < 1: B(α; β) I remind you that the beta function can be expressed by the gamma function: Γ(α)Γ(β) B(α; β) = : (1) Γ(α + β) In Lee, x 3.1 is shown that the posterior distribution is a beta distribution as well, πjx ∼ beta(α + x; β + n − x): (Because of this result we say that the beta distribution is conjugate distribution to the binomial distribution.) We shall now derive the predictive distribution, that is finding p(x).
    [Show full text]
  • 9. Binomial Distribution
    J. K. SHAH CLASSES Binomial Distribution 9. Binomial Distribution THEORETICAL DISTRIBUTION (Exists only in theory) 1. Theoretical Distribution is a distribution where the variables are distributed according to some definite mathematical laws. 2. In other words, Theoretical Distributions are mathematical models; where the frequencies / probabilities are calculated by mathematical computation. 3. Theoretical Distribution are also called as Expected Variance Distribution or Frequency Distribution 4. THEORETICAL DISTRIBUTION DISCRETE CONTINUOUS BINOMIAL POISSON Distribution Distribution NORMAL OR Student’s ‘t’ Chi-square Snedecor’s GAUSSIAN Distribution Distribution F-Distribution Distribution A. Binomial Distribution (Bernoulli Distribution) 1. This distribution is a discrete probability Distribution where the variable ‘x’ can assume only discrete values i.e. x = 0, 1, 2, 3,....... n 2. This distribution is derived from a special type of random experiment known as Bernoulli Experiment or Bernoulli Trials , which has the following characteristics (i) Each trial must be associated with two mutually exclusive & exhaustive outcomes – SUCCESS and FAILURE . Usually the probability of success is denoted by ‘p’ and that of the failure by ‘q’ where q = 1-p and therefore p + q = 1. (ii) The trials must be independent under identical conditions. (iii) The number of trial must be finite (countably finite). (iv) Probability of success and failure remains unchanged throughout the process. : 442 : J. K. SHAH CLASSES Binomial Distribution Note 1 : A ‘trial’ is an attempt to produce outcomes which is neither sure nor impossible in nature. Note 2 : The conditions mentioned may also be treated as the conditions for Binomial Distributions. 3. Characteristics or Properties of Binomial Distribution (i) It is a bi parametric distribution i.e.
    [Show full text]
  • Chapter 6 Continuous Random Variables and Probability
    EF 507 QUANTITATIVE METHODS FOR ECONOMICS AND FINANCE FALL 2019 Chapter 6 Continuous Random Variables and Probability Distributions Chap 6-1 Probability Distributions Probability Distributions Ch. 5 Discrete Continuous Ch. 6 Probability Probability Distributions Distributions Binomial Uniform Hypergeometric Normal Poisson Exponential Chap 6-2/62 Continuous Probability Distributions § A continuous random variable is a variable that can assume any value in an interval § thickness of an item § time required to complete a task § temperature of a solution § height in inches § These can potentially take on any value, depending only on the ability to measure accurately. Chap 6-3/62 Cumulative Distribution Function § The cumulative distribution function, F(x), for a continuous random variable X expresses the probability that X does not exceed the value of x F(x) = P(X £ x) § Let a and b be two possible values of X, with a < b. The probability that X lies between a and b is P(a < X < b) = F(b) -F(a) Chap 6-4/62 Probability Density Function The probability density function, f(x), of random variable X has the following properties: 1. f(x) > 0 for all values of x 2. The area under the probability density function f(x) over all values of the random variable X is equal to 1.0 3. The probability that X lies between two values is the area under the density function graph between the two values 4. The cumulative density function F(x0) is the area under the probability density function f(x) from the minimum x value up to x0 x0 f(x ) = f(x)dx 0 ò xm where
    [Show full text]
  • 3.2.3 Binomial Distribution
    3.2.3 Binomial Distribution The binomial distribution is based on the idea of a Bernoulli trial. A Bernoulli trail is an experiment with two, and only two, possible outcomes. A random variable X has a Bernoulli(p) distribution if 8 > <1 with probability p X = > :0 with probability 1 − p, where 0 ≤ p ≤ 1. The value X = 1 is often termed a “success” and X = 0 is termed a “failure”. The mean and variance of a Bernoulli(p) random variable are easily seen to be EX = (1)(p) + (0)(1 − p) = p and VarX = (1 − p)2p + (0 − p)2(1 − p) = p(1 − p). In a sequence of n identical, independent Bernoulli trials, each with success probability p, define the random variables X1,...,Xn by 8 > <1 with probability p X = i > :0 with probability 1 − p. The random variable Xn Y = Xi i=1 has the binomial distribution and it the number of sucesses among n independent trials. The probability mass function of Y is µ ¶ ¡ ¢ n ¡ ¢ P Y = y = py 1 − p n−y. y For this distribution, t n EX = np, Var(X) = np(1 − p),MX (t) = [pe + (1 − p)] . 1 Theorem 3.2.2 (Binomial theorem) For any real numbers x and y and integer n ≥ 0, µ ¶ Xn n (x + y)n = xiyn−i. i i=0 If we take x = p and y = 1 − p, we get µ ¶ Xn n 1 = (p + (1 − p))n = pi(1 − p)n−i. i i=0 Example 3.2.2 (Dice probabilities) Suppose we are interested in finding the probability of obtaining at least one 6 in four rolls of a fair die.
    [Show full text]
  • Chapter 5 Sections
    Chapter 5 Chapter 5 sections Discrete univariate distributions: 5.2 Bernoulli and Binomial distributions Just skim 5.3 Hypergeometric distributions 5.4 Poisson distributions Just skim 5.5 Negative Binomial distributions Continuous univariate distributions: 5.6 Normal distributions 5.7 Gamma distributions Just skim 5.8 Beta distributions Multivariate distributions Just skim 5.9 Multinomial distributions 5.10 Bivariate normal distributions 1 / 43 Chapter 5 5.1 Introduction Families of distributions How: Parameter and Parameter space pf /pdf and cdf - new notation: f (xj parameters ) Mean, variance and the m.g.f. (t) Features, connections to other distributions, approximation Reasoning behind a distribution Why: Natural justification for certain experiments A model for the uncertainty in an experiment All models are wrong, but some are useful – George Box 2 / 43 Chapter 5 5.2 Bernoulli and Binomial distributions Bernoulli distributions Def: Bernoulli distributions – Bernoulli(p) A r.v. X has the Bernoulli distribution with parameter p if P(X = 1) = p and P(X = 0) = 1 − p. The pf of X is px (1 − p)1−x for x = 0; 1 f (xjp) = 0 otherwise Parameter space: p 2 [0; 1] In an experiment with only two possible outcomes, “success” and “failure”, let X = number successes. Then X ∼ Bernoulli(p) where p is the probability of success. E(X) = p, Var(X) = p(1 − p) and (t) = E(etX ) = pet + (1 − p) 8 < 0 for x < 0 The cdf is F(xjp) = 1 − p for 0 ≤ x < 1 : 1 for x ≥ 1 3 / 43 Chapter 5 5.2 Bernoulli and Binomial distributions Binomial distributions Def: Binomial distributions – Binomial(n; p) A r.v.
    [Show full text]
  • A Note on Skew-Normal Distribution Approximation to the Negative Binomal Distribution
    WSEAS TRANSACTIONS on MATHEMATICS Jyh-Jiuan Lin, Ching-Hui Chang, Rosemary Jou A NOTE ON SKEW-NORMAL DISTRIBUTION APPROXIMATION TO THE NEGATIVE BINOMAL DISTRIBUTION 1 2* 3 JYH-JIUAN LIN , CHING-HUI CHANG AND ROSEMARY JOU 1Department of Statistics Tamkang University 151 Ying-Chuan Road, Tamsui, Taipei County 251, Taiwan [email protected] 2Department of Applied Statistics and Information Science Ming Chuan University 5 De-Ming Road, Gui-Shan District, Taoyuan 333, Taiwan [email protected] 3 Graduate Institute of Management Sciences, Tamkang University 151 Ying-Chuan Road, Tamsui, Taipei County 251, Taiwan [email protected] Abstract: This article revisits the problem of approximating the negative binomial distribution. Its goal is to show that the skew-normal distribution, another alternative methodology, provides a much better approximation to negative binomial probabilities than the usual normal approximation. Key-Words: Central Limit Theorem, cumulative distribution function (cdf), skew-normal distribution, skew parameter. * Corresponding author ISSN: 1109-2769 32 Issue 1, Volume 9, January 2010 WSEAS TRANSACTIONS on MATHEMATICS Jyh-Jiuan Lin, Ching-Hui Chang, Rosemary Jou 1. INTRODUCTION where φ and Φ denote the standard normal pdf and cdf respectively. The This article revisits the problem of the parameter space is: μ ∈( −∞ , ∞), σ > 0 and negative binomial distribution approximation. Though the most commonly used solution of λ ∈(−∞ , ∞). Besides, the distribution approximating the negative binomial SN(0, 1, λ) with pdf distribution is by normal distribution, Peizer f( x | 0, 1, λ) = 2φ (x )Φ (λ x ) is called the and Pratt (1968) has investigated this problem standard skew-normal distribution.
    [Show full text]
  • 3 Multiple Discrete Random Variables
    3 Multiple Discrete Random Variables 3.1 Joint densities Suppose we have a probability space (Ω, F, P) and now we have two discrete random variables X and Y on it. They have probability mass functions fX (x) and fY (y). However, knowing these two functions is not enough. We illustrate this with an example. Example: We flip a fair coin twice and define several RV’s: Let X1 be the number of heads on the first flip. (So X1 = 0, 1.) Let X2 be the number of heads on the second flip. Let Y = 1 − X1. All three RV’s have the same p.m.f. : f(0) = 1/2, f(1) = 1/2. So if we only look at p.m.f.’s of individual RV’s, the pair X1,X2 looks just like the pair X1,Y . But these pairs are very different. For example, with the pair X1,Y , if we know the value of X1 then the value of Y is determined. But for the pair X1,X2, knowning the value of X1 tells us nothing about X2. Later we will define “independence” for RV’s and see that X1,X2 are an example of a pair of independent RV’s. We need to encode information from P about what our random variables do together, so we introduce the following object. Definition 1. If X and Y are discrete RV’s, their joint probability mass function is f(x, y)= P(X = x, Y = y) As always, the comma in the event X = x, Y = y means “and”.
    [Show full text]
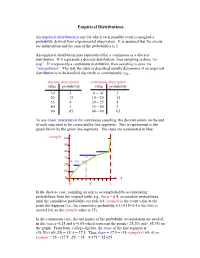
  • Discrete Distributions: Empirical, Bernoulli, Binomial, Poisson
    Empirical Distributions An empirical distribution is one for which each possible event is assigned a probability derived from experimental observation. It is assumed that the events are independent and the sum of the probabilities is 1. An empirical distribution may represent either a continuous or a discrete distribution. If it represents a discrete distribution, then sampling is done “on step”. If it represents a continuous distribution, then sampling is done via “interpolation”. The way the table is described usually determines if an empirical distribution is to be handled discretely or continuously; e.g., discrete description continuous description value probability value probability 10 .1 0 – 10- .1 20 .15 10 – 20- .15 35 .4 20 – 35- .4 40 .3 35 – 40- .3 60 .05 40 – 60- .05 To use linear interpolation for continuous sampling, the discrete points on the end of each step need to be connected by line segments. This is represented in the graph below by the green line segments. The steps are represented in blue: rsample 60 50 40 30 20 10 0 x 0 .5 1 In the discrete case, sampling on step is accomplished by accumulating probabilities from the original table; e.g., for x = 0.4, accumulate probabilities until the cumulative probability exceeds 0.4; rsample is the event value at the point this happens (i.e., the cumulative probability 0.1+0.15+0.4 is the first to exceed 0.4, so the rsample value is 35). In the continuous case, the end points of the probability accumulation are needed, in this case x=0.25 and x=0.65 which represent the points (.25,20) and (.65,35) on the graph.
    [Show full text]
  • Hand-Book on STATISTICAL DISTRIBUTIONS for Experimentalists
    Internal Report SUF–PFY/96–01 Stockholm, 11 December 1996 1st revision, 31 October 1998 last modification 10 September 2007 Hand-book on STATISTICAL DISTRIBUTIONS for experimentalists by Christian Walck Particle Physics Group Fysikum University of Stockholm (e-mail: [email protected]) Contents 1 Introduction 1 1.1 Random Number Generation .............................. 1 2 Probability Density Functions 3 2.1 Introduction ........................................ 3 2.2 Moments ......................................... 3 2.2.1 Errors of Moments ................................ 4 2.3 Characteristic Function ................................. 4 2.4 Probability Generating Function ............................ 5 2.5 Cumulants ......................................... 6 2.6 Random Number Generation .............................. 7 2.6.1 Cumulative Technique .............................. 7 2.6.2 Accept-Reject technique ............................. 7 2.6.3 Composition Techniques ............................. 8 2.7 Multivariate Distributions ................................ 9 2.7.1 Multivariate Moments .............................. 9 2.7.2 Errors of Bivariate Moments .......................... 9 2.7.3 Joint Characteristic Function .......................... 10 2.7.4 Random Number Generation .......................... 11 3 Bernoulli Distribution 12 3.1 Introduction ........................................ 12 3.2 Relation to Other Distributions ............................. 12 4 Beta distribution 13 4.1 Introduction .......................................
    [Show full text]
  • Statistical Distributions
    CHAPTER 10 Statistical Distributions In this chapter, we shall present some probability distributions that play a central role in econometric theory. First, we shall present the distributions of some discrete random variables that have either a finite set of values or that take values that can be indexed by the entire set of positive integers. We shall also present the multivariate generalisations of one of these distributions. Next, we shall present the distributions of some continuous random variables that take values in intervals of the real line or over the entirety of the real line. Amongst these is the normal distribution, which is of prime importance and for which we shall consider, in detail, the multivariate extensions. Associated with the multivariate normal distribution are the so-called sam- pling distributions that are important in the theory of statistical inference. We shall consider these distributions in the final section of the chapter, where it will transpire that they are special cases of the univariate distributions described in the preceding section. Discrete Distributions Suppose that there is a population of N elements, Np of which belong to class and N(1 p) to class c. When we select n elements at random from the populationA in n −successive trials,A we wish to know the probability of the event that x of them will be in and that n x of them will be in c. The probability will Abe affected b−y the way in which theA n elements are selected; and there are two ways of doing this. Either they can be put aside after they have been sampled, or else they can be restored to the population.
    [Show full text]
  • Some Continuous and Discrete Distributions Table of Contents I
    Some continuous and discrete distributions Table of contents I. Continuous distributions and transformation rules. A. Standard uniform distribution U[0; 1]. B. Uniform distribution U[a; b]. C. Standard normal distribution N(0; 1). D. Normal distribution N(¹; ). E. Standard exponential distribution. F. Exponential distribution with mean ¸. G. Standard Gamma distribution ¡(r; 1). H. Gamma distribution ¡(r; ¸). II. Discrete distributions and transformation rules. A. Bernoulli random variables. B. Binomial distribution. C. Poisson distribution. D. Geometric distribution. E. Negative binomial distribution. F. Hypergeometric distribution. 1 Continuous distributions. Each continuous distribution has a \standard" version and a more general rescaled version. The transformation from one to the other is always of the form Y = aX + b, with a > 0, and the resulting identities: y b fX ¡ f (y) = a (1) Y ³a ´ y b FY (y) = FX ¡ (2) Ã a ! E(Y ) = aE(X) + b (3) V ar(Y ) = a2V ar(X) (4) bt MY (t) = e MX (at) (5) 1 1.1 Standard uniform U[0; 1] This distribution is \pick a random number between 0 and 1". 1 if 0 < x < 1 fX (x) = ½ 0 otherwise 0 if x 0 · FX (x) = x if 0 x 1 8 · · < 1 if x 1 ¸ E(X) = 1:=2 V ar(X) = 1=12 et 1 M (t) = ¡ X t 1.2 Uniform U[a; b] This distribution is \pick a random number between a and b". To get a random number between a and b, take a random number between 0 and 1, multiply it by b a, and add a. The properties of this random variable are obtained by applying¡ rules (1{5) to the previous subsection.
    [Show full text]
  • Discrete Random Variables and Probability Distributions
    Discrete Random 3 Variables and Probability Distributions Stat 4570/5570 Based on Devore’s book (Ed 8) Random Variables We can associate each single outcome of an experiment with a real number: We refer to the outcomes of such experiments as a “random variable”. Why is it called a “random variable”? 2 Random Variables Definition For a given sample space S of some experiment, a random variable (r.v.) is a rule that associates a number with each outcome in the sample space S. In mathematical language, a random variable is a “function” whose domain is the sample space and whose range is the set of real numbers: X : R S ! So, for any event s, we have X(s)=x is a real number. 3 Random Variables Notation! 1. Random variables - usually denoted by uppercase letters near the end of our alphabet (e.g. X, Y). 2. Particular value - now use lowercase letters, such as x, which correspond to the r.v. X. Birth weight example 4 Two Types of Random Variables A discrete random variable: Values constitute a finite or countably infinite set A continuous random variable: 1. Its set of possible values is the set of real numbers R, one interval, or a disjoint union of intervals on the real line (e.g., [0, 10] ∪ [20, 30]). 2. No one single value of the variable has positive probability, that is, P(X = c) = 0 for any possible value c. Only intervals have positive probabilities. 5 Probability Distributions for Discrete Random Variables Probabilities assigned to various outcomes in the sample space S, in turn, determine probabilities associated with the values of any particular random variable defined on S.
    [Show full text]